2022年高考全國乙卷物理25題解法探析

蔣 敏 蘭銀燕

(1.西南大學附屬中學校;2.西南大學科學教育研究中心)

2022年高考全國乙卷25題題目情境新穎,有多個研究對象,多個物理過程,綜合性較強,其中物理模型的結合與設問的巧妙都體現出非常強的創新性。題目涉及的物理過程是學生熟悉的兩物塊彈性碰撞過程以及斜面上的勻變速直線運動過程,但題目推陳出新,將兩次彈性碰撞與斜面上的運動巧妙融合在一起,考查學生對高中必備知識的理解與靈活應用程度,滲透物理學科核心素養,該題整體難度較大,體現了高考的選拔性功能。

1.原題呈現

【題目】(2022·全國乙卷·25)如圖1(a),一質量為m的物塊A與輕質彈簧連接,靜止在光滑水平面上;物塊B向A運動,t=0時與彈簧接觸,到t=2t0時與彈簧分離,第一次碰撞結束,A、B的v-t圖像如圖1(b)所示。已知從t=0到t=t0時間內,物塊A運動的距離為0.36v0t0。A、B分離后,A滑上粗糙斜面,然后滑下,與一直在水平面上運動的B再次碰撞,之后A再次滑上斜面,達到的最高點與前一次相同。斜面傾角為θ(sinθ=0.6),與水平面光滑連接。碰撞過程中彈簧始終處于彈性限度內。求:

a

(1)第一次碰撞過程中,彈簧彈性勢能的最大值;

(2)第一次碰撞過程中,彈簧壓縮量的最大值;

(3)物塊A與斜面間的動摩擦因數。

本題主要考查物理學科核心素養中的運動與相互作用觀念和能量觀念,考查動量守恒、機械能守恒、動能定理等核心知識的理解掌握程度,著重考查了科學思維中的模型建構、科學推理等要素。該題第(1)問需要學生根據題目的文字表述、情境示意圖建立碰撞模型,再從v-t圖像中提取有效信息分析兩物塊相互作用過程中的關鍵狀態,再利用動量守恒和機械能守恒解決。第(2)問需要對碰撞過程進行更詳細地分析,列出該過程動量守恒的式子,明確碰撞過程每個時刻兩物塊的速度關系,再用微元疊加的思想求解出A、B的位移關系,進而求解彈簧的最大壓縮量。第(3)問首先要分析“最高點相同”隱含的物理前提是到達斜面的初速度相同,對物塊A在斜面上的運動建立勻變速直線運動模型,分階段應用動能定理,再對A、B的再次碰撞應用動量守恒建立方程,最后聯立解出動摩擦因數。

2.多種解法探析

2.1 第1問解析

物塊B開始壓縮彈簧的一小段時間,A加速,B減速,由于B的速度大于A的速度,彈簧壓縮量逐漸增大,彈性勢能逐漸增加。當A、B速度相同時,彈簧壓縮量最大,彈性勢能最大。在這個過程中,A、B和彈簧組成的系統水平方向無外力作用,動量守恒。

根據動量守恒定律

mB·1.2v0=(mB+m)v0

解得mB=5m

方法一:根據機械能守恒定律

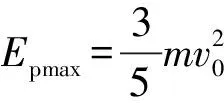
方法二:對物塊A、B分別應用動能定理

由Epmax=-(WA+WB)

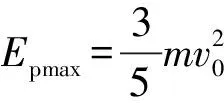
【評析】方法一是運用動量守恒定律和機械能守恒定律解決碰撞模型的一種基本方法,學生對這種方法較為熟悉,上手比較容易。方法二運用了動能定理和彈力做功的特點求解,這種方法可以加深學生對功能關系的理解,對勢能變化與產生勢能的力做功的關系有更深刻的認識。

2.2 第2問解析

彈簧壓縮量的最大值等于物塊B與物塊A在0到t0這段時間運動的距離之差,由題意可知物塊A運動的距離為0.36v0t0,所以關鍵是解出物塊B在這段時間運動的距離。

方法一:在t=0到t=t0時間內的任意時刻,A、B的加速度大小分別為

某時刻,A、B的瞬時速度分別為

vA=∑aAΔt①

vB=1.2v0-∑aBΔt②

由①+5②得vA+5vB=6v0

對每一小段位移疊加求和,得

即xA+5xB=6v0t0

代入xA=0.36v0t0

解得xB=1.128v0t0

所以彈簧壓縮量的最大值

Δx=xB-xA=0.768v0t0

方法二:在t=0到t=t0時間內的任意時刻,A、B系統動量守恒

5m·1.2v0=mvA+5mvB

即6v0=vA+5vB

后面過程與方法一相同。

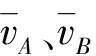
上式每項乘上t0,得

即6v0t0=xA+5xB

后面過程與方法一相同。

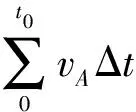
2.3 第3問解析

物塊A第二次到達斜面的最高點與第一次相同,說明第二次碰撞結束的速度大小仍為2v0,方向水平向右。取B的初速度方向為正方向,對第二次碰撞由動量守恒可得

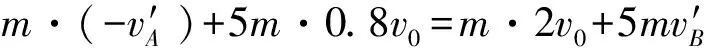
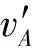
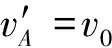
方法一:設物塊A在斜面上向上滑行的長度為l,對第一次在斜面上的運動過程,根據動能定理有

下滑過程,根據動能定理有

聯立解得μ=0.45

方法二:物塊A沿斜面上滑時

mgsinθ+μmgcosθ=ma1

02-(2v0)2=2(-a1)l

物塊A沿斜面下滑時

mgsinθ-μmgcosθ=ma2

聯立解得μ=0.45

【評析】該問既可以利用牛頓第二定律加運動學的規律求解,也可以應用能量守恒或動能定理求解,應用能量規律求解往往可以避開物體運動的細節分析,思路較為簡潔,且計算簡單,不易出錯。

3.對第2問物理過程的深入分析

對于A、B兩物塊的彈性碰撞過程,可分兩個階段分析,在0到t0時間內,隨著彈簧壓縮量的增加彈力增大,A做加速度逐漸增大的加速運動,B做加速度逐漸增大的減速運動;在t0到2t0時間內,隨著彈簧壓縮量的減小,彈力減小,A做加速度逐漸減小的加速運動,B做加速度逐漸減小的減速運動,直到彈簧恢復原長兩者分離。

由于系統水平方向不受任何外力作用,所以兩物塊的質心C做勻速直線運動,速度為

如圖2所示,選質心C為參考系,物塊A與右邊一段彈簧構成一個彈簧振子,做簡諧運動,A相對于質心C的速度為

vAC=v1sin(ωt+φA)

圖2

A相對于地面的速度

vA=vC+vAC=v0+v1sin(ωt+φA)

同理,B相對于地面的速度

vB=vC+vBC=v0+v2sin(ωt+φB)

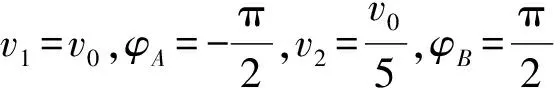
所以

可見A、B整體以v0速度做勻速直線運動,同時相對質心做簡諧運動。既然A、B兩物塊的運動情況是確定的,那么它們在t=0到t=t0時間內的位移就可以解出。

A在t=0到t=t0這段時間的位移

代入A的速度表達式,有

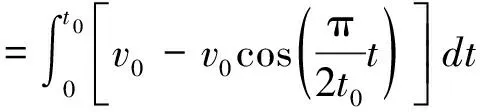
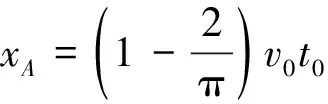
同理,B在t=0到t=t0這段時間的位移

代入B的速度表達式,有

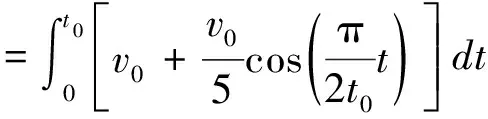
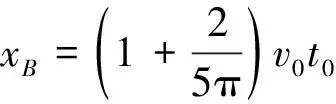
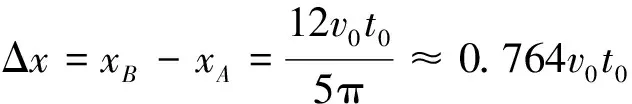
解出的結果與參考答案基本一致。

由于A、B兩物塊相對于質心做簡諧運動,因此也可以通過系統振動的周期求出彈簧的勁度系數,再由彈簧的彈性勢能公式得出彈簧的最大壓縮量。設k為彈簧勁度系數,A、B兩物塊相對于質心做簡諧運動的周期

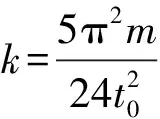
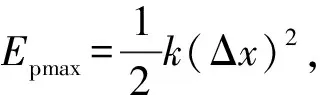
4.教學導向與啟示

教學應注重培養學生的分析綜合能力。對于一個復雜的物理過程,一般地說,總是先采用分析的方法,把過程分為若干部分加以研究;然后再采用綜合的方法,把這些部分結合成為一個整體加以分析。本題作為高考物理的壓軸題,過程復雜、綜合性強,可以分成如下三個階段:兩物塊的彈性碰撞、物塊沿斜面上滑下滑、再次彈性碰撞,需要對每一個階段分別加以研究,找到相應的物理規律列出式子,然后再綜合求解。

在教學中需要創設物理情境促進學生的深度學習,把握物理知識與規律的本質內涵和聯系,要深刻理解物理中的核心與主干知識,不能簡單地記憶公式。比如本題中的第(2)問對彈簧最大壓縮量的求解難度較大,只是簡單記住碰撞模型動量守恒、能量守恒的學生根本無從下手,需要學生對彈簧壓縮過程兩物塊的運動進行仔細分析,建立任意時刻的速度關系,再進行微元疊加求和,解出物塊的位移。如果在平時的教學中教師通過“動畫”模擬過類似的物理過程,并且分別用牛頓運動定律、動量、能量的規律向學生分析兩物塊的速度變化規律,那么學生遇到類似的問題就會得心應手。