基于深度強化學習的高超聲速飛行器動態面控制方法*

胥 彪，趙琛鈺，李 爽，朱東方

(1.南京航空航天大學 航天學院·南京·211106；2.南京航空航天大學 空間光電探測與感知工業和信息化部重點實驗室·南京·211106；3.上海航天控制技術研究所·上海·201109)

0 引 言

高超聲速飛行器因具有機動能力強、飛行距離遠、生存能力強等多重特點，在空間競爭中的重要性愈發凸顯。在飛行任務需求不斷提高的背景下，飛行環境日益復雜，且高超聲速飛行器自身所具有的強非線性、復雜耦合效應、快速時變特性和較大的不確定性等[1]，都對控制系統的設計提出了更高的要求。

目前，已有大量文獻根據反步控制、自適應控制、魯棒控制和模糊控制等多種控制理論，提出了高超聲速飛行器控制方法。例如，Sun H.等[2]基于干擾觀測器的反步控制方法，提出了在虛擬控制律中引入擾動估計以補償不匹配擾動的策略，設計了不犧牲標稱控制性能的自抗擾控制器。Hu X.等[3]針對高超聲速飛行器的參數不確定性和未建模動態，利用模糊邏輯系統(Fuzzy Logical System，FLS)對系統進行辨識，并設計了一種具有較高效率的自適應模糊控制器。Shou Y.等[4]針對系統動力學不確定性，利用在線數據神經網絡學習和擾動觀測器構造了預設時間的Terminal滑模控制器，實現了系統在定義時間內收斂的效果。Bu X.等[5]針對傳統預設性能控制設計中需要預先知道初始跟蹤誤差的限制，提出了一種性能函數以實現不需要精確初始跟蹤誤差的更加簡潔的控制結構和更低計算負擔的控制方法。反步控制憑借其固有的處理系統非線性的能力和閉環系統的自然穩定性而受到廣泛關注，但是由于在設計中存在“項爆炸”的問題，使得控制器在設計時的計算十分復雜。D.Swaroop等[6]通過在非線性系統中引入一階濾波器代替求導工作，可以克服反步設計時的計算復雜問題，并保證了系統跟蹤誤差的有界性。然而，在傳統控制方法中，控制律通常需要設定固定的結構和參數，而一些自適應方法又需要設計復雜的自適應律，從而加深了控制器的設計難度。

隨著高超聲速飛行器的快速發展，對控制系統的智能化要求也不斷提高，這就需要對控制系統各個關鍵環節進行智能化的升級改造，使得飛行器具有智能學習能力[7-9]。將深度學習的感知能力和強化學習的決策能力相結合的深度強化學習(Deep Reinforcement Learning，DRL)是一種通過感知環境變化，以深度神經網絡構建智能體與環境進行交互，并以最大化獎勵為目標訓練智能體得到最優策略的方法。傳統控制方法與先進的人工智能的關系不是簡單的替代關系，而是應該探索一種結合兩者優點的智能控制方法。文獻[10]通過估計值函數，采用基于策略迭代的單網絡積分型強化學習算法，解決了傳統HJB方程難以求解的問題，設計了收斂速度更快的再入飛行器的自適應最優控制器。

由T.P. Lillicrap于2016年提出的深度確定性策略梯度(Deep Deterministic Policy Gradient，DDPG)算法[11]，是深度強化學習中最具代表性的算法之一。確定性策略梯度(Deterministic Policy Gradient，DPG)算法雖然可以處理連續動作空間的任務，但是無法從高維輸入中學習策略[12]。而深度Q網絡(Deep Q-Network，DQN)雖然可以直接進行端到端的學習，卻無法處理離散動作空間的問題[13]。DDPG在DPG的基礎上引入DQN算法的成功經驗，實現了對高維連續動作空間強化學習問題的求解。文獻[14]就利用DDPG算法，以多數據幀的狀態信息作為智能體的觀察狀態，舵偏角和發動機推力指令作為智能體的輸出動作，再經過訓練后得到了具有泛化性和魯棒性的智能飛行控制器。文獻[15]將DDPG和反步法結合，在考慮執行器約束的情況下使控制律中的參數調整得到有效解決。文獻[16]將自抗擾控制算法和強化學習結合，提出了高超聲速飛行器巡航段的智能控制方法。文獻[17]基于深度強化學習理論，設計了導彈攔截問題的制導控制一體化算法。通過強化學習算法，使得導彈可以低能耗快速穩定地攔截目標。文獻[18]在速度子系統設計中采用強化學習算法，設計了基于神經網絡自適應的PID參數智能調整方案。

本文設計了一種用于高超聲速飛行器的姿態跟蹤智能控制算法，目的是在考慮控制約束和性能最優的情況下實現姿態跟蹤控制。其核心思想是建立在傳統動態面控制方法基礎上，使用DRL完成對控制器參數的智能優化，并且在DRL自身訓練過程中達到性能最優的要求。當系統存在不確定性的情況下，智能控制算法仍能完成姿態控制。通過引入DRL算法，實現了在考慮控制量消耗和性能最優情況下的控制器參數智能優化。

1 高超聲速飛行器數學模型

考慮發動機關機狀態下，高超聲速飛行器縱向非線性模型可以表示為如下形式[19]

(1)

式中，彈道傾角γ、攻角α和俯仰角速率ω是描述飛行器縱向姿態運動的3個狀態變量；V、m和r分別代表了飛行器目前飛行速度、質量和距地心的徑向距離；μ為重力常數；I為轉動慣量；Δ表示系統不確定項。飛行器的升力L和俯仰力矩M表達式如下

(2)

式中，ρ為空氣密度；S為參考面積；c為平均氣動弦長。升力系數CL和俯仰力矩系數CM的表達式為

(3)

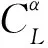
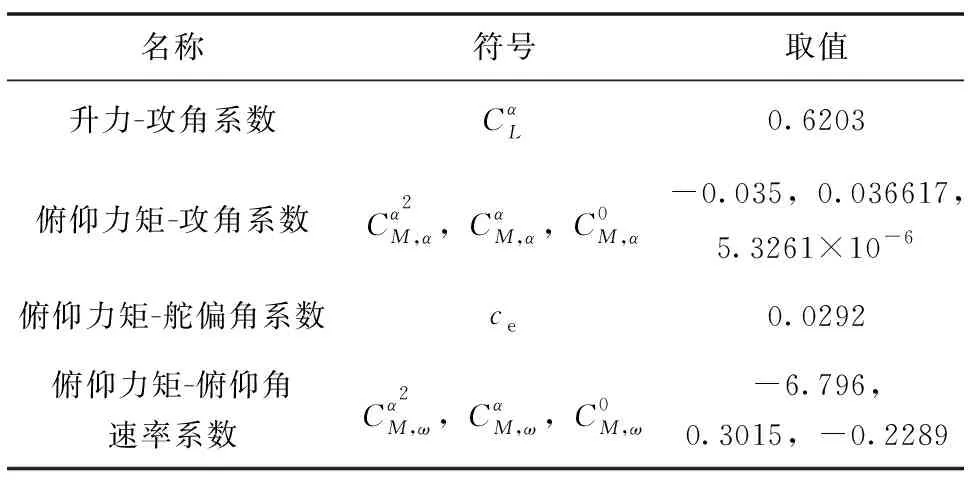
表1 高超聲速飛行器縱向非線性模型參數表

結合實際情況，考慮升降舵偏轉角的幅值約束

-30°≤δ≤30°

(4)

在設計高超聲速飛行器控制律時，動態面控制方法的參數會直接影響控制效果。而傳統方法中，設計參數是依靠人工經驗調試的。本文采用動態面控制設計了控制器結構，將控制系數作為待定量，然后采用強化學習方法進行智能參數優化。

2 控制器設計

首先，利用動態面控制方法[6]分別設計攻角虛擬控制律、俯仰角速率虛擬控制律和升降舵偏轉角控制律。然后，將問題轉化到強化學習環境中，轉為尋找一個最優策略函數實現跟蹤性能和控制量最優。通過將強化學習算法與動態面控制方法結合，完成控制器參數智能優化。

2.1 動態面控制器設計

2.1.1 攻角虛擬控制律設計

首先，定義彈道傾角跟蹤誤差S1為

S1=γ-γd

(5)

令

(6)

對式(6)求導可得

(7)

(8)

其中，k1>0為控制增益。

(9)

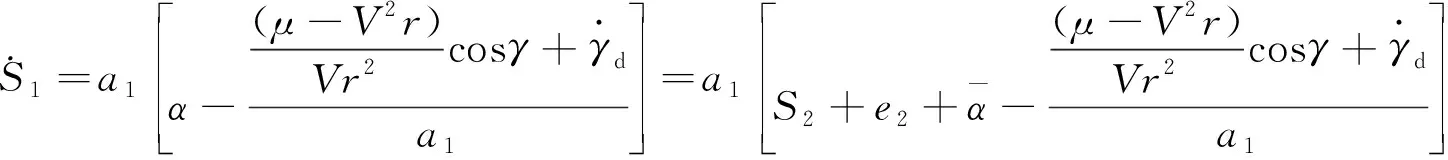
(10)

(11)

2.1.2 俯仰角速率虛擬控制律設計

對攻角跟蹤誤差S2求導得

(12)

此時，設計虛擬控制律為

(13)

其中，k2>0為控制增益。

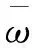
(14)

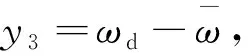
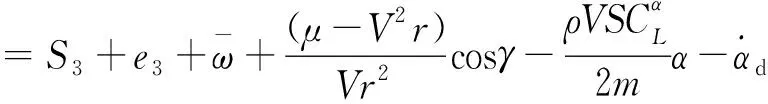
=S3+e3-k2S2

(15)

(16)

2.1.3 升降舵偏轉角控制律設計

令

(17)

(18)

對俯仰角速率跟蹤誤差S3求導得

(19)

此時，設計最終的控制律為

(20)

其中，k3>0為控制增益；ρ3>|Δ|是阻尼項系數；ε為任意小的正實數。

(21)

對于Lyapunov函數V=V1+V2+V3，求導得

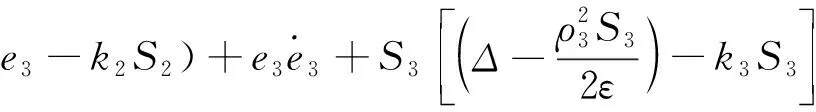
=a1S1S2+a1S1e2+S2S3+S2e3+

(22)

由式(8)和式(13)推導濾波誤差的導數為

(23)

由式(23)可知，存在非負連續函數B2、B3，滿足不等式

(24)

(25)

則可得

(26)

假設V(0)=p，當V≤p成立時，考慮緊集

(27)

(28)

其中，χ是足夠大的正數。故此時Ω1×Ω2也是緊集。由此可知，在V≤p成立時，Bi(i=2，3)在Ω1×Ω2上有最大值，記為Mi。

由于ρ3≥|Δ|，可得

(29)

此時，對式(22)進一步處理可得

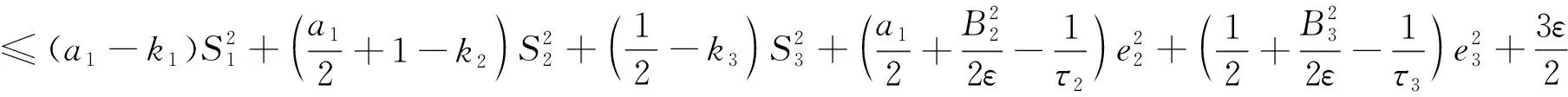
(30)

故按如下條件設計控制參數

(31)

(32)

其中，d≥0為待設計的正數，此時

(33)

然后將式(33)兩邊同乘以e2dt，再在[0，t]上對其積分得

(34)

故可得閉環系統狀態是有界的，并且當ε充分小時，可以保證系統跟蹤誤差足夠小。實際應用中，采用人工試錯方式進行調參，在很大程度上依賴于調試人員的經驗，比較繁瑣。本文采用深度強化學習方法設計控制器參數的智能優化算法，實現對彈道傾角指令的跟蹤。

2.2 基于深度強化學習的高超聲速飛行器控制器參數優化設計

2.2.1 馬爾可夫決策過程

本文的姿態控制問題符合馬爾可夫性，即未來狀態的概率分布僅依賴于當前狀態。按照馬爾可夫決策過程，在時刻t的狀態值可僅依靠上一時刻t-1的狀態值由式(1)得到。此時，假設遵循策略π(S)，控制參數為k=π(S)，可以得到下述軌跡

S0,k0,R0,S1,k1,R1,……,St,kt,Rt,……

(35)

其中，Rt為t時刻的獎勵值。St和kt分別為

St=[S1t,S2t,S3t]T,kt=[k1t,k2t,k3t]T

(36)

其中，St為在t時刻的狀態向量；kt為在t時刻的動作值向量。Sit和kit分別表示在t時刻Si和ki的值，i=1，2，3。問題就轉化為了尋找一個最優策略π*(S)，使得控制過程中的跟蹤誤差和控制量消耗最小。即在采取最優策略得到的式(35)的軌跡中，其獎勵值總和最大。

為了衡量策略函數在給定狀態時采取動作的優劣，定義回報Gt為t時刻開始往后所有獎勵的衰減總和

(37)

其中，γRL為折扣因子。定義狀態動作值函數Q(St，kt)為在狀態St下采取動作kt會收到的回報，由式(37)可得

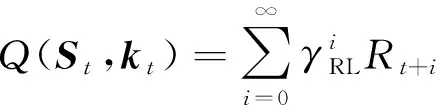
(38)

這樣當前時刻的狀態動作值函數就可以由下一時刻的狀態動作值函數計算得到。

2.2.2 DDPG控制參數尋優算法

根據文獻[11]，構建4個神經網絡，且Critic網絡輸出值為Q(St，kt|θ)，θ為該評價網絡的權值參數；Critic目標網絡輸出值為Q′(St，kt|θ′)，θ′為該目標評價網絡的權值參數；Actor當前網絡輸出值為π(St|φ)，φ為該策略網絡的權值參數；Actor目標網絡輸出值為π′(St|φ′)，φ′為該目標策略網絡的權值參數。

在訓練中的探索部分，利用策略網絡π(St|φ)輸出原始動作值并與噪聲疊加得到kt與環境交互

kt=π(St|φ)+N

(39)

其中，N為引入的OU噪聲以增強對環境的探索，然后將與環境得到的樣本(St，kt，Rt，St+1)存入經驗回放池D中。在網絡更新部分，為實現深度神經網絡訓練時要求的樣本無關性，從經驗回放池中隨機取出N個樣本進行訓練。假設n=1，2，3，…，N，對隨機取出的樣本重新編號為(Sn，kn，Rn，Sn+1)。Q(Sn，kn|θ)的目標是擬合下列目標函數

yn=Rn+γRLQ′(Sn+1,π′(Sn+1|φ)|θ′)

(40)

此時，損失函數為最小化均方誤差

(41)

然后，采用梯度下降方法完成對Critic網絡的更新。

為了使Actor網絡不斷地向更優的策略擬合，則其更新方向需按照使Q(Sn，kn|θ)增大的方向進行優化。其梯度更新公式為

(42)

其余2個目標網絡則在每個訓練回合完成后進行軟更新

θ′←τθ+(1-τ)θ′
φ′←τφ+(1-τ)φ′

(43)

其中，τ∈(0，1)為慣性參數。

整個控制結構如圖1所示。

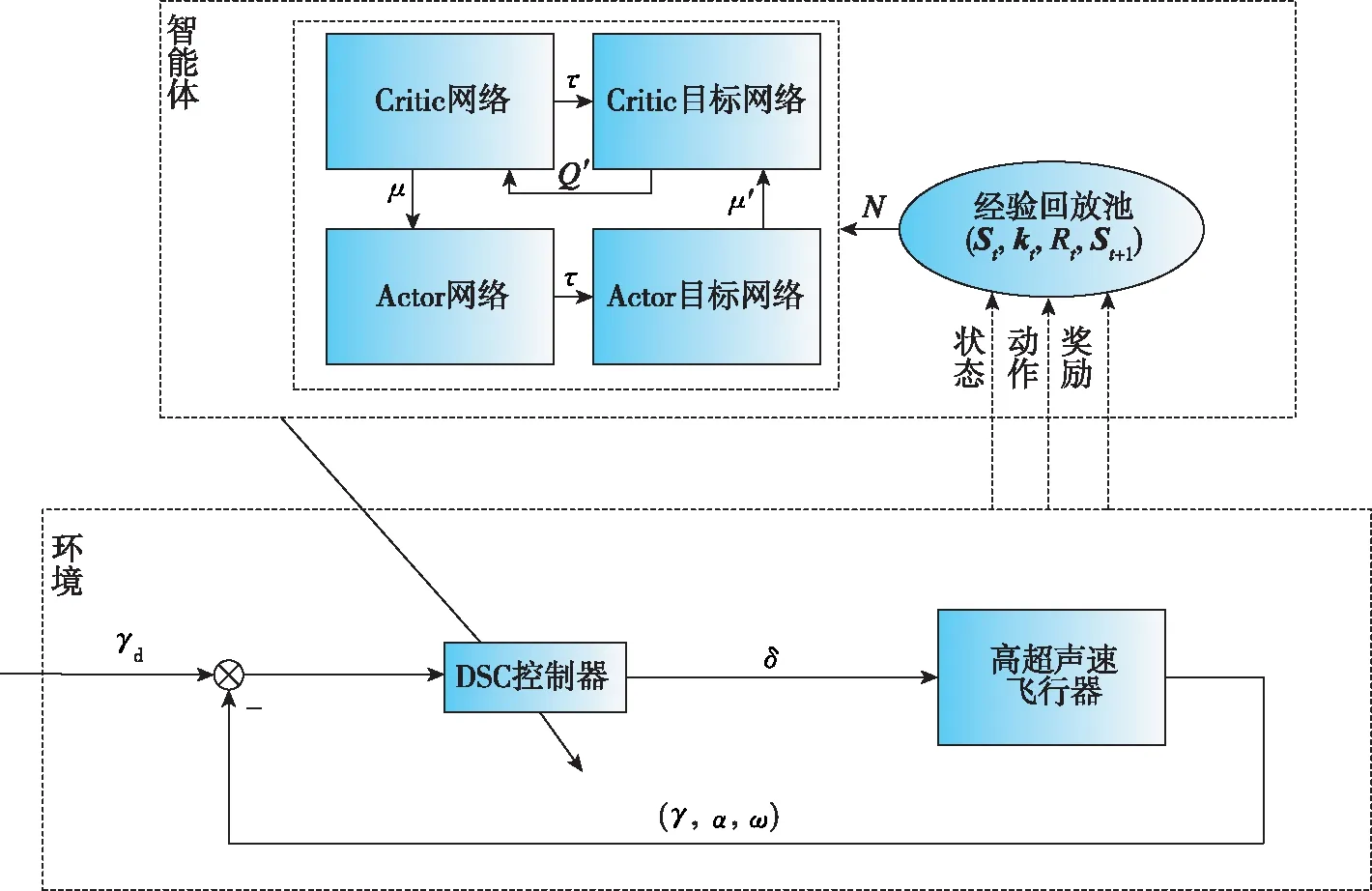
圖1 高超聲速飛行器智能控制框圖Fig.1 Hypersonic vehicle intelligent control block diagram

綜上所述，基于DDPG的高超聲速飛行器智能優化算法訓練過程如表2所示。

表2 基于DDPG的高超聲速飛行器智能優化算法

3 仿真分析

3.1 DDPG智能體訓練

選用飛行參數[19]為速度V=4590m/s，質量m=1.378×105kg，轉動慣量I=9.5×106kg·m2，大氣密度ρ=0.0125368kg/m3，平均氣動弦長c=24.4m，參考面積S=335.2m2，地心距r=6.4×106m。式(1)中取Δ=0.01sin(0.2t)rad/s2，其余參數取ρ3=0.01，ε=0.01，μ=3.936×1014，d=0.5。低通濾波器的時間常數為τ2=0.01，τ3=0.1。選擇跟蹤目標為γd=10sin(0.1t)°。訓練中高超聲速飛行器的各變量約束如表3所示。

表3 高超聲速飛行器的狀態約束

Actor網絡隱含層中使用三層全連接網絡；Critic網絡隱含層中同樣使用全連接網絡。Actor網絡的輸出層激活函數采用tanh函數g1(z)，使其輸出位于(-1，1)之間，以此保證控制輸入約束在容許范圍內，除此之外其余網絡的激活函數均選擇使用Relu函數g2(z)作為激活函數

(44)

訓練的相關參數如表4所示。

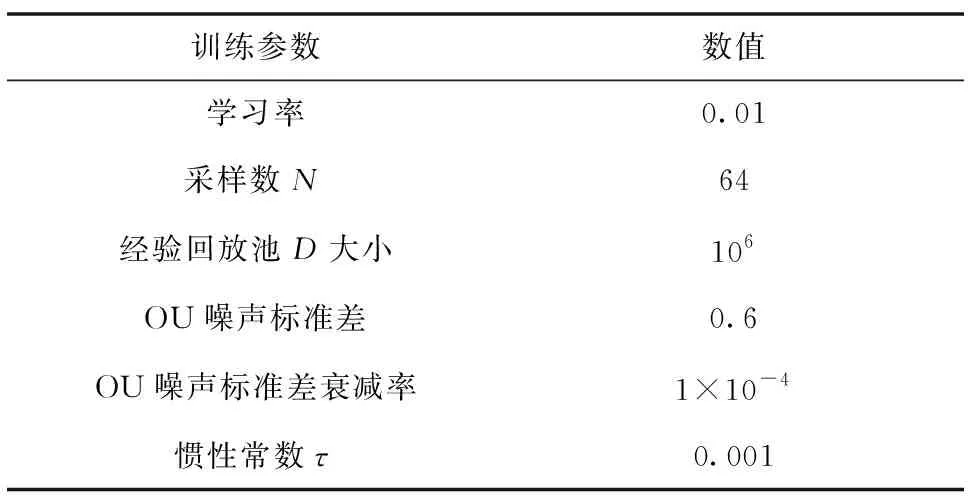
表4 訓練參數設置

獎勵函數的設置是強化學習訓練的關鍵，結合本文問題，將獎勵函數R設計為如下形式

(45)

式中，ks是跟蹤誤差權重系數，ku是控制量權重系數；γmax、δmax分別為彈道傾角和升降舵偏轉角所設定的最大值；Ra是獎勵函數中引入的控制量變化率

(46)

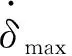
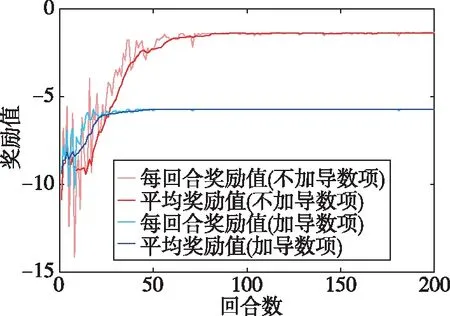
圖2 獎勵曲線Fig.2 Reward curve

由圖2可知，在獎勵函數未加導數的情況下，獎勵曲線在第74回合之后獎勵值到達并保持在終值的5%誤差以內；而在加入獎勵導數項之后，獎勵曲線在第25回合就達到了上述標準，并且后者的曲線在前幾個回合內的獎勵值更加平穩。

3.2 姿態控制仿真結果

圖3～圖6所示為標稱情況下的控制效果。由圖可以看出，在加入導數項后，加快訓練速度的同時能夠保證控制效果。

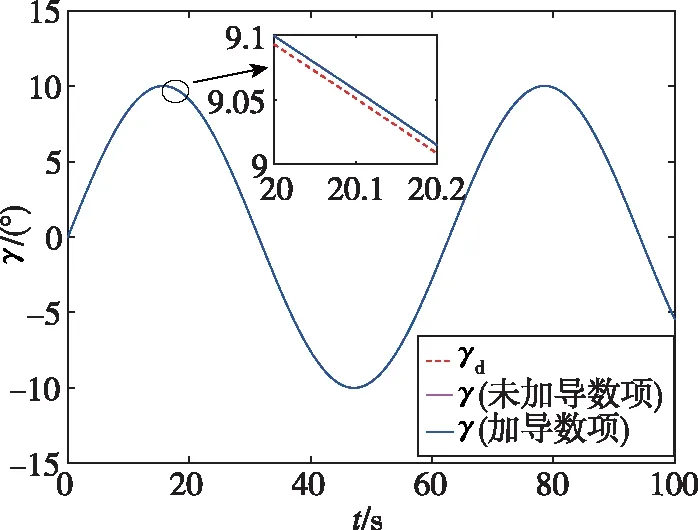
圖3 彈道傾角跟蹤曲線Fig.3 Flight path angle tracking curve

圖6 升降舵偏轉角變化曲線Fig.6 Elevator curve

為了驗證所設計控制器對參數不確定性的適應能力，對氣動參數在標稱值±50%內進行拉偏處理，執行300次蒙特卡羅仿真實驗，實驗結果如圖7和圖8所示。從圖中可以看出，在系統存在不確定性的情況下，控制算法可以適應系統不確定性帶來的變化，具有較好的魯棒性。

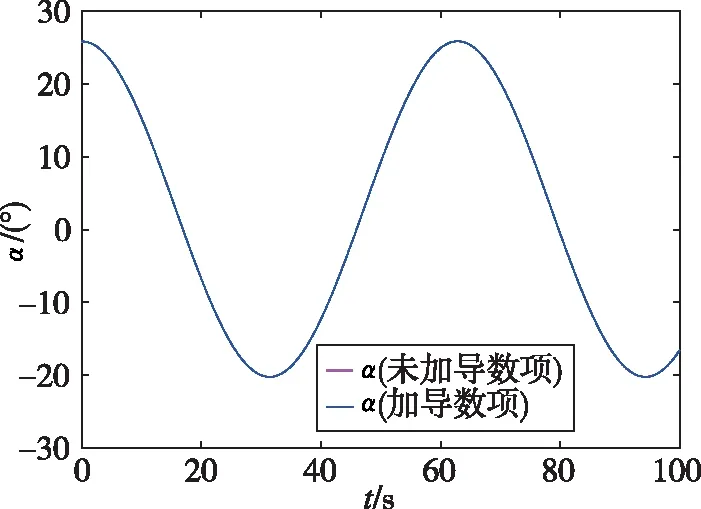
圖4 攻角變化曲線Fig.4 Attack of angle curve

圖5 俯仰角加速度變化曲線Fig.5 Pitch angle curve

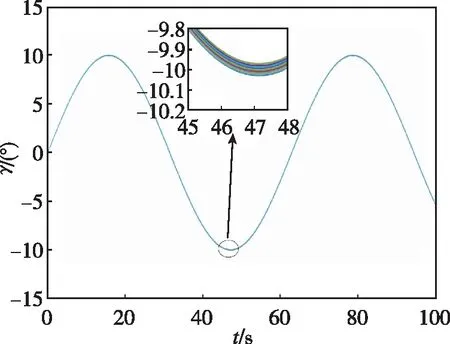
圖7 不確定條件下彈道傾角變換曲線Fig.7 Flight path angle curve under uncertainty

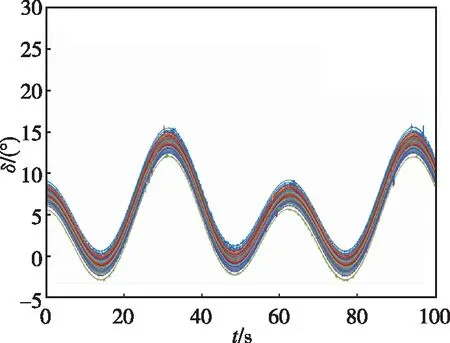
圖8 不確定條件下舵偏角變換曲線Fig.8 Elevator curve under uncertainty

4 結 論

本文針對高超聲速飛行器姿態控制問題，設計了一種基于DRL的動態面智能優化控制算法。通過結合DRL機制的尋優思想，完成對動態面控制的參數智能尋優，代替了傳統的參數調整過程與時間消耗，構建出智能控制器。經仿真結果表明，該控制器可以在考慮控制量消耗的情況下實現高性能的穩定跟蹤控制，且在考慮氣動參數不確定性情況下仍能保持良好的跟蹤效果。