大學物理與高中物理光學部分的教學銜接研究

朱云龍　任永志　李玉祥

關(guān)鍵詞 大學物理;中學物理;單縫衍射;半波帶法;光程對稱關(guān)系

高中物理對光學部分的教學和考察通常以幾何光學為主、波動光學為輔，且在波動光學部分以定性了解為主、以定量分析為輔。以衍射為例，普通高中物理課程標準（2017年版2020年修訂）選擇性必修1中要求學生“觀察光的干涉、衍射和偏振現(xiàn)象，了解這些現(xiàn)象產(chǎn)生的條件，知道其在生產(chǎn)生活中的應(yīng)用”，但不要求學生定量分析衍射產(chǎn)生的明暗條紋位置[1]。

大學物理與中學物理不同，在光學部分重視波動光學，且以定量分析為主。由于普通高中物理課程標準對干涉部分的要求包括“會用雙縫干涉實驗測量光的波長”[1]，因此高中畢業(yè)生通常具有雙縫干涉定量分析的基礎(chǔ);但從干涉向衍射的過渡涉及惠更斯菲涅耳原理的應(yīng)用，具有一定的思維跨度，導(dǎo)致部分學生難以理解掌握衍射部分的授課內(nèi)容。

幫助學生銜接高中物理知識并拓展其分析解決問題能力是大學物理教學的重要課題[2]。目前大學物理與高中物理光學部分的銜接已有相關(guān)研究發(fā)表[3]，然而其中教學銜接難度較大的衍射部分卻未見具體的改進教學方案報導(dǎo)。本文以夫瑯禾費單縫衍射的講解為例，分析比對了目前大學物理中衍射的常見講解方法，并利用光程對稱關(guān)系對基于惠更斯菲涅耳原理的半波帶法原理論證過程進行簡化。這一教學方法課堂反饋良好，可以為大學物理教師以及有意拓展光學部分課外知識的中學物理教師提供參考。

1 夫瑯禾費單縫衍射的常見講解方法

夫瑯禾費單縫衍射作為最基本的衍射模型，是衍射部分教學的要點。目前大學課堂教學通常采用的講解方法包括惠更斯菲涅耳積分法、振幅矢量疊加法以及菲涅耳半波帶法三種[4，5]。

惠更斯菲涅耳積分法是一種定量的分析方法，可以精確給出衍射光強表達式[6]。然而，通過積分推導(dǎo)明暗條紋位置的過程對于低年級本科生或課外拓展學習的高中生等授課對象而言難度較大，且物理圖像不直觀;此外，該方法講解耗時較長，受限于授課時間安排，教師通常無法詳細講解積分過程。

振幅矢量疊加法的思想是將每個次波源所對應(yīng)的光矢量首尾相接，當取的次波源尺寸趨近無窮小時，矢量首尾相接的曲線變?yōu)楣饣膱A弧，計算合矢量振幅大小的極值即可準確獲取明暗條紋位置[4，7-9]。該方法直觀性上優(yōu)于積分法，但推導(dǎo)的過程仍然較為復(fù)雜，且求解過程涉及超越方程，不適合高中生或低年級本科生的課堂授課。

與以上兩種方法相比，菲涅耳半波帶法更常見于衍射部分的授課過程中，因其物理模型與計算過程更為簡潔、直觀，也更易于被學生接受[10，11]。雖然菲涅耳半波帶法的計算結(jié)果與惠更斯菲涅耳積分法之間存在一定的偏差[6，7]，但利用該方法卻可在較短的時間內(nèi)，使學生理解單縫衍射的基本原理，并掌握計算明紋與暗紋位置的方法。半波帶法的主要不足之處為缺乏對于半波帶模型合理性的定量剖析，可引起部分學生對于該方法科學性的質(zhì)疑;若要剖析半波帶法的原理，則只能引出授課時間較長、理解難度較大的惠更斯菲涅耳積分法或振幅矢量疊加法。下文將簡要介紹夫瑯禾費單縫衍射中半波帶法的原理，并針對傳統(tǒng)半波帶法講解過程中的不明晰之處給出一種新的教學思路。

2 夫瑯禾費單縫衍射與半波帶法

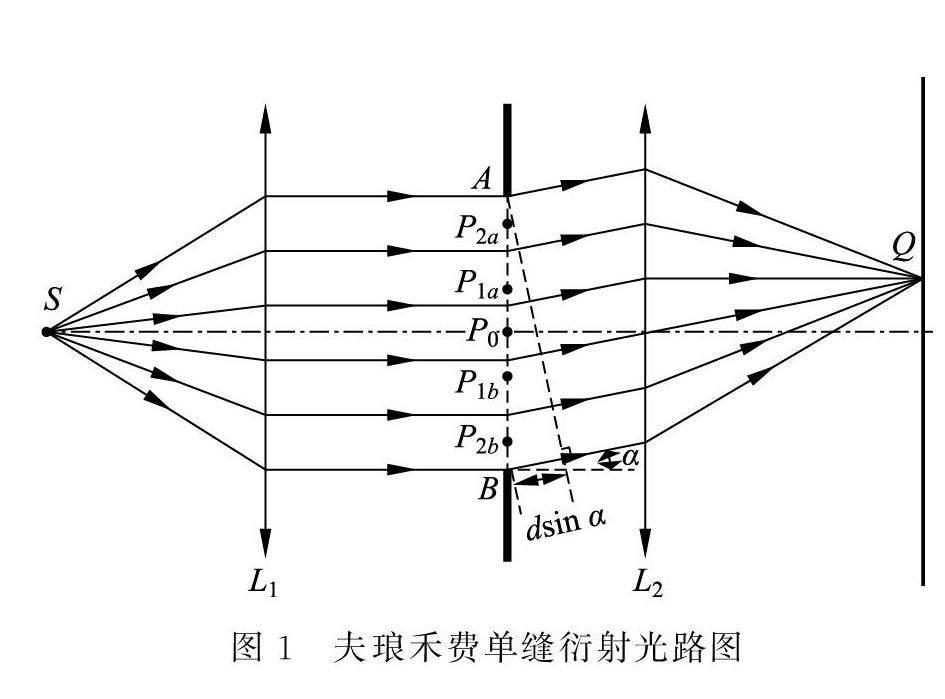
夫瑯禾費單縫衍射的光路圖如圖1所示。點光源S 發(fā)出的單色相干光經(jīng)凸透鏡L1 擴束、準直后，經(jīng)平行照射單縫AB。根據(jù)惠更斯菲涅耳原理，A 點與B 點之間的每個點都可視為次波的波源，且所有次波相干;入射光經(jīng)過單縫后以水平方向夾角α 斜向上出射的部分經(jīng)過透鏡L2 匯聚于屏上Q 點，Q 點可發(fā)生相干增強或相干減弱，分別對應(yīng)衍射明紋或暗紋。

設(shè)單縫AB 寬度為d，則B 點至Q 點的光程與A 點至Q 點的光程之間的差值δ 為

δ=dsina （1）

設(shè)入射光波長為λ，則當δ 為λ/2的奇數(shù)倍或0時，Q 點為相干增強的明條紋;當δ 為λ/2的偶數(shù)倍（不包括0）時，Q 點為相干減弱的暗條紋。該確定明暗條紋位置的方法，由于以半波長λ/2為參考因此被稱為“半波帶法”。半波帶法雖然直觀，但課堂上受限于學生基礎(chǔ)與時間限制，一般只采用定性的解釋，其原理剖析深度不足，會給學生對于該知識點的理解與記憶帶來一定的困擾。

3 利用光程對稱關(guān)系簡化教學

對于低年級本科生或進行課外擴展學習的高中生而言，衍射的學習與理解通常具有較高難度，主要原因是理解衍射需引入高等數(shù)學中的微積分思想，將兩個分量的干涉擴展為無數(shù)個子波源的干涉，因此普通高中物理課程標準只要求定性講解衍射現(xiàn)象。

針對以上問題，為了高效完成從中學物理到大學物理關(guān)于夫瑯禾費單縫衍射教學的銜接，本文基于半波帶法，借鑒振幅矢量疊加法，根據(jù)光程對稱關(guān)系提出一種新的教學方法。首先，將單縫處光場分解為無數(shù)振幅相等的子波源，根據(jù)惠更斯菲涅耳原理，可知所有子波源在屏上相干疊加形成衍射條紋。其次，圍繞單縫中心點，根據(jù)光程對稱關(guān)系，將每一對位置對稱的子波源兩兩疊加，所獲得光場相位均與單縫中心點子波源相位相同，但光場振幅均與特定數(shù)值相乘。最后，由于相位相同，屏上各子波源的相干疊加可轉(zhuǎn)化為簡單的數(shù)值疊加，根據(jù)所疊加數(shù)值的正負號特性，即可獲得“當δ 為λ/2的奇數(shù)倍或0時，Q 點為相干增強的明條紋;當δ 為λ/2的偶數(shù)倍（不包括0）時，Q 點為相干減弱的暗條紋”這一定量結(jié)論，從而闡明半波帶法的基本原理。

該講解方法物理含義清晰，在大一年級大學物理教學的實踐中獲得了良好的效果;此外，該方法亦有助于學生快速理解后續(xù)教學內(nèi)容中的光柵衍射缺級現(xiàn)象。該方法的具體原理如下文所述。

在圖1中，假設(shè)單縫光強均勻，則單縫上任一微元的光場強度表達形式為

4 教學效果分析

本文所述的講解方法從兩個子波源之間的干涉入手，利用光程對稱關(guān)系，結(jié)合三角函數(shù)和差化積公式或矢量相加性質(zhì)，使微積分基礎(chǔ)較弱的學生也能理解半波帶法的原理與應(yīng)用。在大學物理課堂實踐中，只選取P₀，P_1a ，P_1b三點作為示例進行講解，即可達到良好的教學效果。

2021年春季學期，在兩個大一年級不同班級的大學物理線下授課實踐中，采用板書的形式進行講解，課堂反映良好。實際消耗時間約5分鐘，對于課程進度的影響較小。此外，由于該方法將有寬度的單縫與寬度無窮小的單縫中心位置P0進行了等效處理，便于學生理解衍射光柵部分的缺級現(xiàn)象，故可在保證教學效果的同時，有效節(jié)約光柵部分的授課時間。

2022年春季學期，對兩個大一年級不同班級進行大學物理線上授課，采用線上板書進行講解，實際耗時同樣約為5分鐘。光學部分授課結(jié)束后，在學生群中發(fā)起無記名問卷，問卷覆蓋了光學部分主要知識點的學習狀況自評。收到學生填寫完整的問卷共19份，其中與半波帶法密切相關(guān)的為四道自我評分題，要求學生對于幾個關(guān)鍵概念的掌握情況進行評分（根據(jù)掌握程度從低到高取0～10之間的整數(shù)），而且對于高中畢業(yè)時與學過大學物理光學部分后分別進行評分。針對相同學生、相同題目，將現(xiàn)階段分數(shù)與高中階段分數(shù)做差，可獲得學生經(jīng)過大學物理課堂學習后的進步分數(shù)。與半波帶法密切相關(guān)的四道題目的問卷統(tǒng)計結(jié)果如表1所示。

提交的問卷中出現(xiàn)了個別問卷的個別題目進步分數(shù)為負的情況，可能由于學生填寫時忙中出錯造成。若將進步分數(shù)為負的題目作為異常數(shù)據(jù)排除，則可得到表1中“去除負數(shù)項平均”分數(shù)值;若考慮到學生填寫問卷的認真程度，將包含負數(shù)項的整張答卷作為異常數(shù)據(jù)排除掉，則可得到表1中“去除負數(shù)答卷平均”分數(shù)值。由表1可知平均的進步分數(shù)約為3分，結(jié)合問卷填寫耗時數(shù)據(jù)判斷，出現(xiàn)負值大概率由于填寫失誤造成，因此“去除負數(shù)答卷平均”數(shù)據(jù)可靠性較高。

就“去除負數(shù)答卷平均”數(shù)據(jù)而言，可見學生對于自己的知識點掌握程度不滿意，高中自評僅約1～2分，推測與高中物理中關(guān)于波動光學的講解大多停留在定性層面、學生基礎(chǔ)較為薄弱相關(guān);學習過大學物理光學部分后，自評分數(shù)明顯提升，但僅達到4～5分左右，推測與學生填寫問卷時剛剛結(jié)束授課、復(fù)習尚未開始有關(guān)。“干涉的原理”與“衍射的原理”為半波帶法的理論基礎(chǔ)，而干涉的掌握情況略好于衍射，與高中物理干涉部分的講解較為詳細的實際情況相符。“光程/光程差的計算”為半波帶法計算的數(shù)學基礎(chǔ)，進步分數(shù)最高，推測與課堂上的重點講授密切相關(guān)。“半波帶法的理解”高中基礎(chǔ)明顯最為薄弱，但經(jīng)過大學物理教學后獲得了較為明顯的提升，可見本文所述的教學方法有益于學生理解。“衍射的原理”部分進步分數(shù)高于“干涉的原理”，從側(cè)面說明衍射部分的整體教學效果獲得了一定提升。

5 結(jié)語

大學物理與中學物理有關(guān)光學部分的授課內(nèi)容差異較大，主要體現(xiàn)為：中學物理側(cè)重光學現(xiàn)象的定性解釋、波動光學要求較低，而大學物理側(cè)重光學現(xiàn)象的定量分析且波動光學要求較高。對于拓展課外知識、為學習大學課程做準備的高中生，或者微積分等數(shù)學工具運用不夠熟練的本科生而言，大學物理光學部分具有較大的難度。大學物理教師授課時若忽視學生中學階段較為薄弱的光學基礎(chǔ)，則會使學生產(chǎn)生“斷層”感，難以跟上學習進度;中學物理教師擴展光學部分內(nèi)容時，若跨度太大，基本原理解釋不清或不做解釋，同樣會使學生產(chǎn)生眾多疑點。因此，教師應(yīng)掌握并理解學生光學部分的水平，尤其是明確學生波動光學基礎(chǔ)較為薄弱這一前提，進而設(shè)計適當?shù)慕虒W方法，逐步夯實基礎(chǔ)，消除學生的疑點，實現(xiàn)大中銜接的平滑過渡。

在光學部分中，大學物理與中學物理對衍射的要求差異尤為明顯，有必要設(shè)計一種既定量、又容易理解的講解方式。本文以夫瑯禾費單縫衍射為例，在學生對于光的干涉掌握情況較好、微積分基礎(chǔ)較為薄弱的情況下，提出一種新的講解方法，即：利用光程對稱關(guān)系首先考慮子波源兩兩干涉的情況，從而在特定出射角將單縫等效為中心位置處寬度無窮小的窄縫，并建立光場疊加后的振幅與單縫寬度以及出射角之間關(guān)系，從而給出半波帶法的物理解釋。該方法講解耗時較短、易于理解，且便于銜接光柵衍射等后續(xù)教學內(nèi)容。在大學物理的線上以及線下教學實踐中，該方法均獲得了良好的教學效果。由此可見，物理教師應(yīng)加強對于學生基礎(chǔ)情況的了解，從而提出針對性更強的教學方法、提升課堂教學效果。