交叉口車車碰撞事故車損程度的影響要素

肖樂 周華 王朝健 劉鑫

關鍵詞：交通安全；交叉口；事故嚴重性；車車事故；雙變量有序Probit模型

據統計[1]，2019年中國大陸發生道路交通事故20萬余起，其中發生在交叉口事故就有4萬余起，占比約22%。且交叉口的數量隨著城鎮化的進程快速增加，導致路網愈加繁雜，各類交通流在此交匯，形成大量交通沖突點，相關研究顯示，發生在城市交叉口的事故占比約30%[2]。因此研究城市交叉口事故嚴重性影響因素對事故預防具有重要意義。

事故嚴重性的分析方法，主要有計量經濟學模型和數據挖掘方法。計量經濟學模型主要包含Logit模型[3-4]和Probit模型[5-6]。袁方等[7]采用隨機參數次序Probit模型對交叉口自行車與機動車碰撞事故進行分析，發現車輛類型、交通信號和交叉路口類型等要素影響事故嚴重性。陳荔等[8]采用多元Logit模型分析不同形態的城市交通事故影響要素，結果表明交通方式、行駛狀態、違法行為3個因素影響最顯著。馬景峰等[9]對采用偏比例優勢模型對電動自行車與機動車事故的影響因素進行分析，發現事故區位、道路類型與光線亮度是可能導致事故高發的因素。

在采用數據挖掘方面，趙曉華等[10]基于導航數據挖掘交叉口風險因素，發現交叉口車道數、信號相位、中央分隔帶類型、監控設備數量等都對交叉口安全性具有顯著影響。汪瑩等[11]歸納交叉口事故影響因素，建立安全評價模型，實現交叉口安全程度的量化分級。此外，也有學者利用交通沖突數量或交通沖突模型進行交通安全分析，郭延永等[12]構建了包含數據層、處理層、先驗層的3層Beyes超閾值沖突極值模型，對非常規信號交叉口的安全影響因素進行了定量評估。王晨等[13]將極值模型與微觀交通仿真相結合，對信號交叉口的交通安全進行評價。

針對事故嚴重性分類，分類方式眾多。美國公路委員會將汽車交通事故傳統地分為死亡、A、B、C級傷害和僅有物損的事故[14]。中國大陸根據事故后果的嚴重程度分為特大事故、重大事故、一般事故與輕微事故[15]。分類方式雖然豐富，但在實際用于研究時，通常只考慮死亡和受傷人數，忽略了車輛損失的影響，而考慮汽車損壞嚴重性的研究則更少。

現有文獻大多采用Probit和Logit等傳統離散模型分析，相關文獻表明采用該類模型分析的效果較好，但尚未見有綜合考慮汽車損壞狀態和人、車、路、環等要素對城市車車事故嚴重性影響的研究報道。

為此，本文以中國國家車輛事故深度調查體系（NationalAutomobileAccidentIn-depthInvestigationSystem，NAIS）中528例交叉口車車事故數據為樣本，建立雙變量有序Probit（bivariateorderedProbit，BOP）概率模型，以車輛損壞狀態為因變量，辨識事故嚴重性影響因素，最后利用平均邊際效應量化顯著因素的影響。本文引入車輛損壞狀態可為事故影響因素分析提供新的視角，可望為減小城市交叉口車車事故數量及降低事故嚴重性提供一定理論支撐。

1數據來源及事故特性分析

對于分析的數據來源，多數研究采用國外開源數據，該數據難以反映具有中國特色的道路交通事故特征；且部分學者以國內某一城市的事故統計數據作為研究對象，難以表征道路交通事故的共性。故本文數據來源于國家車輛事故深度調查體系（NAIS）。

該體系由國家市場監督管理總局缺陷管理中心聯合8所具有較深事故研究背景的高校、事故鑒定機構及科研機構共同建立，各工作站采用統一的標準從事故相關的人、車、路、環信息進行深入采集，并完成事故再現分析。2011—2019年，共已收集4000多起道路交通事故案例，覆蓋全國7個地區包括東北、華南、西南、華北、華東等地。該數據主要由交通事故采集人通過到事故現場復勘和交警部門獲得，包括事故照片、編碼的數據、警方資料、事故現場視頻、事故重構文件、CAD（computeraideddesign，計算機輔助設計）事故現場圖以及事故分析報告等。數據完整、詳細，對交通事故研究具有較高價值。

本文從數據庫中篩選事故地點類型為城市路口（三枝和四枝交叉口）共得到556起事故數據，剔除并清洗信息記錄不全數據，最終共獲得有效數據528起作為研究對象。

1.1城市路口事故特性分析

1.1.1時間特性

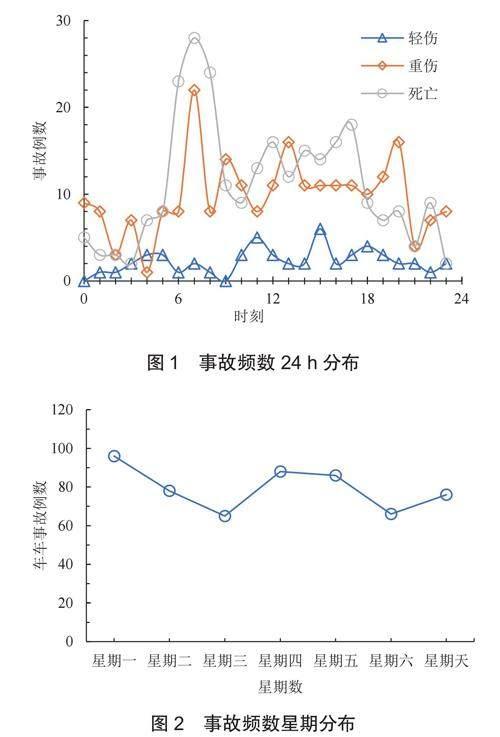
圖1為1日（24h）內的城市路口事故頻數分布。圖2為1星期內事故頻數分布。

由圖1可知：不同嚴重程度的24h事故分布均呈現“雙高峰”，但高峰時刻存在微小差異。其中重傷、死亡事故的第1次高峰時刻為07：00—07：59，死亡事故的第2次高峰時刻為17：00—17：59，重傷事故的為20：00—20：59，其余時段為平峰段。在06：00—08：00的重傷、死亡事故數量分別為38起、75起，整體的死亡事故數量大于重傷事故數量，這與城市交叉口上班早高峰所具有的交通高密度、大流量密切相關，根據該時間分布特性可為交叉口事故預防提供一定的決策依據。

由圖2可知：1周內事故數量分布呈“W”形，其中星期一發生車車事故數最多（96例），逐漸下降到星期三，隨后上漲，最后從星期五逐漸下降。由于星期一是工作日的第一天，出行率高，造成的交通事故也最多；周末休息，城市居民出行率明顯降低，交通沖突隨之降低，事故數量也顯著少于工作日。

1.1.2車輛損壞狀態特性

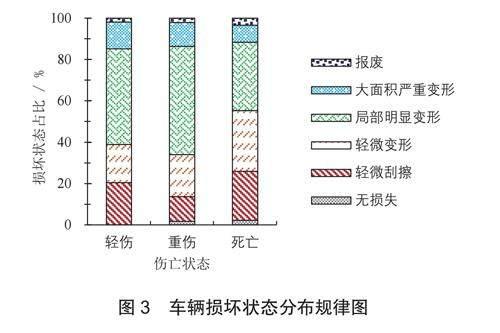
根據統計的事故傷亡情況來看，城市交叉口受傷事故占比53.03%，超事故總數的一半以上。圖3為傷亡事故的車輛損壞狀態分布圖。從圖3可知：一半以上的重傷事故會造成車輛局部明顯變形，輕傷事故造成車輛大面積嚴重變形的概率最大。對于這類事故而言，事故傷亡嚴重性小，但車輛損壞卻很嚴重，因此有必要從車輛損壞狀態角度分析交叉口事故嚴重程度影響因素。

1.2事故嚴重性分析

1.2.1因變量

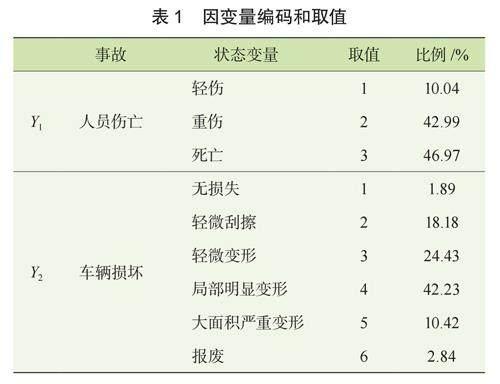
原始數據將事故嚴重程度分為4個等級：輕微事故（僅輕傷）、一般事故（重傷、未死亡）、重大事故（死亡1～2人）、特大事故（死亡3人及以上）。由于特大事故僅在此分析中僅1例，故將其與重大事故歸為一類；其中車輛損壞狀態為各參與方車輛整體的損失程度。最終確定本文的事故嚴重程度具體情況如表1。

1.2.2自變量

調研國內外學者對交叉口事故影響因素選取情況，并結合數據事故特征，從人、車、道路、環境4個方面選擇15個自變量，采用方差膨脹因子對變量之間的共線性情況進行診斷，當方差膨脹因子在0到10之間表示變量間不存在多重共線性。各變量取值見表2。

結果表明：15個自變量之間無多重共線性。

2研究方法

2.1雙變量有序Probit模型

具體形式如下：

式中：Y1*代表人員傷亡事故的潛在變量；Y2*代表車輛損失的潛在變量；X1i、X2i分別為人員傷亡事故和車輛損失事故的解釋變量；β1、β2為對應X1i、X2i的參數估計值，ε1i、ε2i為誤差項；i對應變量數；γ為待估參數項。Y1、Y2代表觀測到的有序變量，則觀測變量與潛在變量的關系為：

在模型擬合過程中，需要對2個假設進行了檢驗。1）使用似然比檢驗獨立性假設，判斷是否使用雙變量模型；2）使用Wald檢驗一致性假設，判斷2個因變量對應的自變量回歸系數是否相同；3）通過逐步回歸，以Akaike（赤池）信息量準則（Akaikeinformationcriterion，AIC）和Bayes信息量準則（Bayesianinformationcriterion，BIC）達到最小為標準得到擬合度最佳的模型。

3車車事故雙變量有序Probit模型結果分析

3.1雙變量有序Probit模型驗證

雙變量有序Probit模型結果表明，誤差項的相關系數為ρ=0.110，p值檢驗小于0.001，說明傷亡和車輛損壞嚴重性間存在正相關關系。同時，Wald檢驗的結果顯著（卡方值X2=95.00，顯著性水平p≤0.001），拒絕2類變量回歸系數相同的假設，說明各因素對2類事故的嚴重程度影響存在差異，在模型中剔除未通過90%水平下的顯著性變量后，模型相關性系數增大，所有變量也全部通過顯著性檢驗，說明模型整體擬合效果好。通過逐步回歸使模型收斂，假設參數向量β使得lnL（β）取值最大，對應的似然函數L（β）=-1160.88，模型擬合優度指標AIC=2351.76，BIC=2415.81，達到最小，說明模型的擬合度取得最佳。同時在不考慮2個因變量間的相關性時，2個獨立的單變量有序Probit模型中AIC=2354.07，BIC=2418.11，均大于雙變量模型，進一步驗證了使用雙變量模型的合理性。

3.2雙變量有序Probit模型結果分析

以事故車輛損失狀態和傷亡狀態為因變量，選取駕駛員因素、車輛類型、道路和環境條件、碰撞位置等因素共包含15個變量為自變量，進行雙變量有序Probit模型擬合，見表3。

雙變量有序Probit模型結果表明：影響傷亡嚴重性的變量中有8個變量系數為正，7個變量系數為負，其中5個變量影響顯著，分別是信號燈狀態、路燈狀態、車輛類型、駕駛員超速駕駛和未按規定讓行。影響車輛損壞狀態的變量中有13個變量系數為正，2個變量系數為負，其中9個變量對車輛損壞狀態影響顯著。用傷亡狀態作為因變量時，共挖掘出5個顯著變量，而引入車輛損失后，能夠挖掘出更多對事故嚴重性影響的潛在易忽略變量。比如性別變量、事故發生時段等，有研究顯示：該要素對事故嚴重性影響不顯著，因此將其剔除；而本文卻發現：其對事故車輛損壞嚴重性影響顯著，有助于交通管理者采取更為合理的策略來降低交叉口事故嚴重性。

3.3模型邊際效應分析

圖4表示傷亡程度變量的平均邊際效應b。圖5為路燈狀態變量平均邊際效應b。

由圖4可知：顯著影響傷亡嚴重性的4個變量中，人為因素對事故嚴重性影響最顯著，其次是交叉口路燈和信號燈狀態，其中超速駕駛變量影響事故死亡的概率最大。

如圖5所示：對于影響車輛損壞嚴重性的6個變量中，邊際效應的變動存在明顯的最高點（4處），在該最高點處會顯著增加車輛局部明顯變形的概率。

圖6為車輛碰撞位置的邊際效應圖。由圖6可知：各變量邊際效應被0刻度線分為上下2層，當車輛碰撞位置在左側時，造成車輛局部明顯、大面積嚴重變形、報廢的概率比正面和右側面碰撞高。

圖7為不同車輛類型的碰撞事故的邊際效應圖。由此可知：乘用車與乘用車碰撞事故造成的車損最為嚴重。

從圖4—7中可以看出：各變量的邊際效應隨著傷亡程度和車輛損失程度取值變動的情況。為量化該變動的大小，對其取值進行詳細分析，見表4、表5。

由表4、5，結合邊際效應數值可以看出：

1）在駕駛員方面。人為因素中駕駛員超速駕駛（β=0.449）對事故傷亡率影響最顯著，使事故死亡概率增加15.49%，其次是未按規定讓行（β=0.258）使事故死亡概率增加9.69%。駕駛員酒后駕駛（β=1.104）對事故車輛損壞嚴重性最顯著，導致車輛報廢的可能性高達5.92%，其次是駕駛員性別（β=-0.409）要素，相關研究發現[16]，當事故無法避免的時候，女性駕駛員在處理事故從而減輕車輛損壞的應急能力稍弱與男性。以往研究通常會忽略性別因素，而分析則表明性別因素可以顯著影響車輛損失嚴重程度。

2）在車輛因素方面。車輛碰撞位置顯著影響事故嚴重性，參與車相對主車從左側面碰撞（β=0.507）對事故嚴重性影響最顯著，造成車輛局部明顯變形的概率增加9.89%，其次是正面碰撞（β=0.438）和右側面碰撞（β=0.389），造成車輛局部明顯變形的概率分別上升7.89%、6.97%。車輛類型方面，從傷亡程度來看，涉及二三輪車的事故傷亡率較高，大多數駕駛員相關研究表明[17]，城市交叉口早、晚高峰期出行流量大，車與非機動車的交通沖突多，受傷事故的數量也相應增加，由于二三輪車駕駛員缺乏保護措施，事故發生后非死即傷。相比二三輪車事故，乘用車與乘用車碰撞造成的車損比乘用車與二三輪車的大，從邊際效應可以看出，乘用車間的碰撞事故造成車輛局部明顯變形的概率比與非機動二三輪車高13.47%，比與機動二三輪車高11.77%；由于二三輪車車速小、質量小，當與乘用車發生碰撞時有足夠的避撞反應時間，因此造成的車輛損失也較小。

3）在道路、環境方面。路燈狀態（β=-0.403）與傷亡嚴重性顯著負相關，結合邊際效應數值可以發現，相比于無路燈狀態，有路燈條件下，可以降低事故死亡概率9.43%。路口信號燈狀態與傷亡和車輛損壞顯著負相關。結合邊際效應可以發現，相比于沒有信號燈，有路口信號燈時，造成死亡事故的概率降低7.55%，還可以明顯降低車輛損失，車輛局部明顯變形的影響最大，使其發生概率降低2.27%。由此可見路口信號燈的狀態，對事故嚴重程度影響較大，說明了交叉口交通信號設施的重要性。

4結論

本文在分析城市交叉口車車事故時間、車輛損失分布特性的基礎上，考慮車輛損壞狀態，構建雙變量有序Probit模型進行事故嚴重程度影響因素分析，主要結論如下：

1）交叉口車車碰撞事故在星期一、星期四和星期五事故數量最大，07：00—07：59時段和17：00—17：59時刻是死亡事故的高峰段，20：00—20：59時段為重傷事故的高發期。

2）通過雙變量有序Probit模型得人為因素、車輛類型、碰撞位置、路燈和信號燈狀態對交叉口車車碰撞車損嚴重性的影響較為顯著；酒后駕駛導致車輛報廢的可能性高達5.92%；相比于沒有信號燈，有信號燈時，發生車輛局部明顯變形概率降低2.27%，明顯降低車輛損失，減輕事故嚴重程度。

3）乘用車與乘用車在交叉口的碰撞事故，造成的車輛損失最嚴重，車輛局部明顯變形的概率比與非機動二三輪車高13.47%，碰撞類型為左側面碰撞顯著影響車輛損失，造成車輛局部明顯變形的概率比右側面碰撞高2.92%。

數據庫收集的字段有限，考慮車損影響因素時不完善，隨著數據庫的充實，有待進一步研究。