HCP分子勢能面和振動光譜研究

張佳美 徐建剛 張云光 張思雨 郭甜 陳艷南

摘 要 ???：本文基于Molpro2019程序包， 采用單雙激發耦合簇方法（CCSD）結合基組cc-pVQZ構建HCP分子的一維勢能曲線和二維勢能曲面， 發現HCP分子面內、面外彎曲振動模式之間的簡并現象以及H-C拉伸振動模式對分子勢能的重要影響. 本文以勢能面為基礎， 首次采用振動多組態自洽場方法（VMCSCF）和振動多參考組態相互作用方法（VMRCI）計算HCP分子的基頻、倍頻、組合頻以及振動能量， 頻率計算值與實驗值吻合較好. 擬合繪制出分子的紅外和拉曼振動光譜， 發現振動模式間的費米共振現象. 本文為含磷星際分子的實驗和理論研究提供了參考.

關鍵詞 ：HCP分子; 勢能面; 振動多參考組態相互作用方法; 振動頻率; 振動光譜

中圖分類號 ：O561 文獻標識碼 ：A DOI ： ?10.19907/j.0490-6756.2023.044001

The potential energy surface and vibrational spectroscopy of HCP molecule

ZHANG Jia-Mei， XU Jian-Gang， ZHANG Yun-Guang，

ZHANG Si-Yu， GUO Tian， CHEN Yan-Nan

（School of Science， Xian University of Posts and Telecommunications， Xian 710000， China）

In this paper， based on the Molpro2019， the one-dimensional potential energy curves and two-dimensional potential energy surfaces of HCP are constructed by using the single and double excitation coupled cluster method（CCSD）combined with the basis set cc-pVQZ. It is found that the degeneracy between the in-plane and out-of-plane bending vibration modes of HCP molecule and the important influence of the tensile vibration mode on the molecular potential energy. Based on the potential energy surface， the fundamentals， overtones， combination bands and vibration energy of HCP are calculated by the vibrational multiconfiguration self-consistent field method （VMCSCF） and vibrational multireference configuration interaction method （VMRCI）. The calculated vibration frequencies are in good agreement with the experimental values. The infrared and Raman spectrum of HCP are further fitted and plotted， and the Fermi resonance between vibration modes is found. This paper provides ?reference for the experimental and theoretical research of phosphorus-related interstellar molecules.

HCP molecule; Potential energy surface; Vibrational multireference configuration interaction method; Vibrational frequency; Vibrational spectrum

1 引 言

HCP分子是星際空間中能探測到的少數含有磷的分子之一. 在PN和CP之后， 它是第三個被發現的含磷星際分子. 研究含磷星際分子對于天體物理和星際磷化學研究具有重要意義， 因此受到專家學者的密切關注.

在實驗觀測方面， 1961年Gier ?［1］首次成功在實驗室條件下制備出了HCP固體聚合物單體， 確定了單體HCP制備的比例， 并在-196°處檢測到固體HCP單體的紅外光譜與HCP結構完全一致， 為HCP結構的研究提供了進一步支持. 隨后， Garneau和Cabana ?［2-5］陸續用不同分辨率的光譜儀實驗觀察到HCP振轉光譜的各個譜帶， 并擬合了指定紅外光譜的所有波數. 2007年， Agúndez和他的團隊 ?［6］使用IRAM 30 m望遠鏡在AGB星周包層IRC+10 216 cm波段處探測到HCP的存在. 這是HCP分子首次在星際介質中被探測到. 在此之前， 研究用到的HCP均基于Gier ?［1］的制備方法制備， 但該方法對制備溫度要求嚴格， 且制備純度有限， 從而導致實驗觀察到的HCP分子的紅外光譜并不準確.

在計算方面， 隨著量子化學領域的發展， 關于HCP分子的量化計算也同步開展 ?［7-10］. 上世紀末至今， 對于HCP分子的量化研究內容主要包括幾何平衡構型、動力學特性、振動能級、勢能面、振動譜等. 1993年， Chen和Chong ?［11］采用deMon密度泛函方法計算了基態HCP分子的勢能面， 并使用FORTRAN 77環境下的TRIATOM程序和DVR程序計算出其振轉能量， 將理論值與實驗值進行了比較. 但該方法存在較大的局限性， 計算精度較差. 1996年， Koput等人 ?［12，13］使用耦合聚類方法和微擾法對HCP分子展開計算， 先后發表了兩篇論文報道了計算得到的幾何結構參數、光譜常數、勢能面和振動能級. 2000年， Koput等人 ?［14］又使用內收縮多參考態組態相互作用方法對HCP分子展開當時最為精確的量化計算， 提出了HCP分子第一個全局精確勢能面， 從而提供了基態HCP分子的完整內部動力學描述. 此外， 圍繞HCP分子， 眾多學者還廣泛開展了對其高激發態振動動力學、同位素分子以及HCP-CPH異構化過程的研究. H ltzl等人 ?［15］使用了多種量子化學方法， 包括CCSD（T）、CASSCF、CASPT2、MR-ACPF和MR-ACPF-2， 研究HCP二聚化體系. 2016年和2020年， Wang等人 ?［16，17］先后報道了采用動態勢法研究得到的HCP及其同位素分子DCP在高激發態下的性能特點.

近二十年來， 多核結構計算水平的提高以及從頭算電子結構理論的發展使得在合理的時間范圍內確定分子體系的勢能面和準確可靠地研究星際分子的動力學特性等相關性質成為可能 ?［18-21］. 2014年， Pfeiffer和Rauhut ?［22］開發了基于特定狀態的多參考振動相互作用方法（VMRCI）. 該方法基于振動多組態自洽場方法（VMCSCF）實現， 能夠實現對體系振動能量的準確計算， 尤其適用于具有強非諧共振和高振動態（倍頻或組合頻）的系統. 本文首次將VMRCI方法應用于HCP分子振動結構計算， 實現了對分子體系振動特性的精確把握. 在計算過程中， 采用CCSD/cc-pVQZ方法優化HCP分子幾何結構， 基于勢能面， 采用VSCF、VMCSCF、VMRCI三種方法層層優化計算， 得到HCP分子的基頻、倍頻和組合頻等振動頻率以及絕對能量， 繪制出精確的紅外和拉曼光譜圖， 為實驗和理論工作提供參考.

2 理論計算

分子光譜和勢能面是研究分子結構的重要工具 ?［23-27］. 本文使用Molpro 2019從頭算程序包， 以波恩-奧本海默近似下的Hartree-Fock（HF）方法作為計算起點， 在CCSD/cc-PVQZ水平確定HCP分子的平衡幾何結構和勢能面擴展所需的簡諧頻率和簡正坐標， 計算出的高水平勢能面為之后的振動計算提供可靠的輸入.

本文采用離散變量表示法求解振動薛定諤方程， 采用VSCF方法計算非諧振動頻率. 考慮到HCP是線性閉殼分子， VSCF的計算采用限制性閉殼HF方法， 薛定諤方程中的沃森哈密頓量展開為

H ︿ = 1 2 ∑ ?αβ ???J ︿ ???α- ?π ︿ ???α ?μ ??αβ ??J ︿ ???β- ?π ︿ ???β -

1 8 ∑ ?α ?μ ??αα- 1 2 ∑ ?i ?????2 ??q ?2 ??i +V ?q ?1，…， q ??3N-6 ??（1）

其中， ?V ?q ?i ?表示勢能面， 它由Molpro程序中的SURF模塊提供， 在簡正坐標下展開. 勢能面函數給出的是分子能量隨幾何形狀變化的函數. 本文研究的所有勢能面都基于多模展開， 在Molpro從頭算程序包中以完全自動化和并行化的方式獲得， 并行化算法允許進行多級計算， 從而加快了計算速度. 多級計算指的是在勢能的多模展開式中， 不同水平的電子結構方法被用于不同的項， 以獲得該項在勢能展開中的貢獻. 勢能面的多級展開具體見式（2）.

由于方程展開中的所有項都是指相對能量而不是總能量， 不影響薛定諤方程的求解結果， 因此這種近似是可行的.

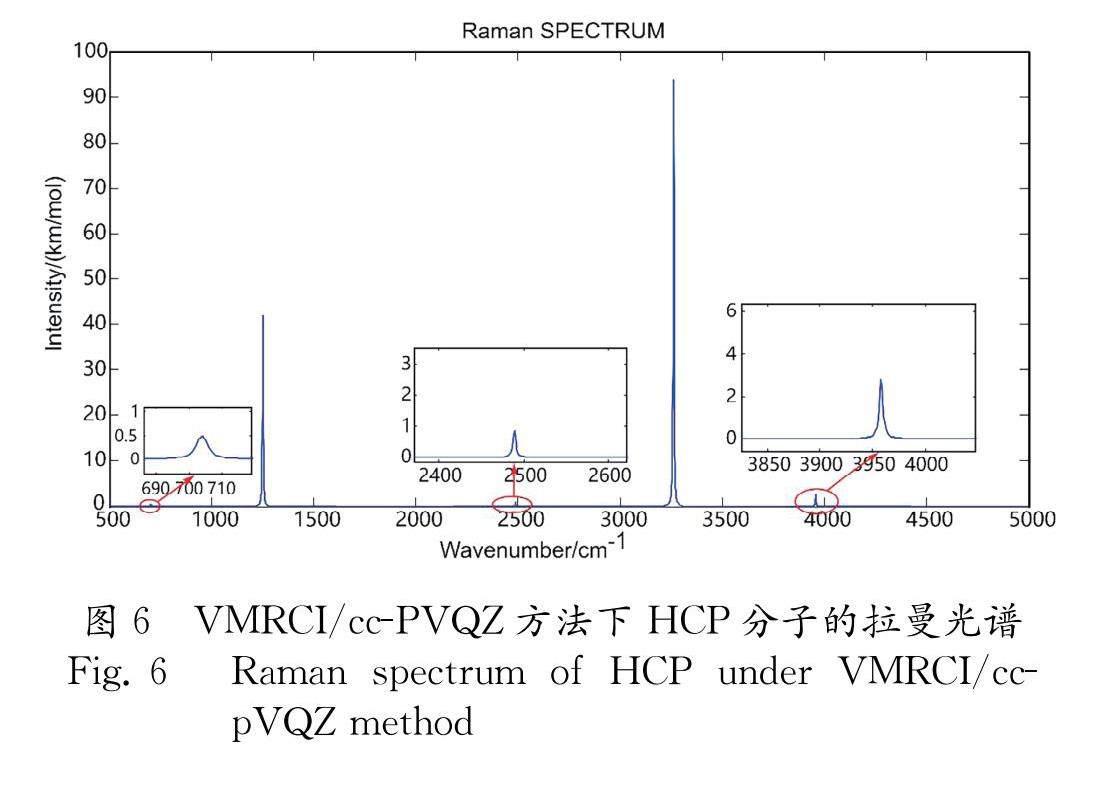
V ?q ?1，…， q ??3N-6 = ?∑ ?i ?V ??i ?q ??i ????1D：CCSD ?+ ?∑ ?i

本文基于勢能面計算了HCP分子的振動結構， 使用VSCF模態作為初始猜測， 再用VMCSCF方法對初始波函數進行優化得到多組態波函數， 考慮相關效應最終展開VMRCI計算. 量化計算基于HF方法展開， 由HF方法產生的誤差稱為相關能誤差. VMCSCF方法通過在波函數中考慮激發組態校正相關能. 考慮的激發組態越多， 校正越大， 計算越精確， 但同時計算時間也會增加. 在VMCSCF計算中， 為了結果的收斂， 激發水平需比勢能展開高一階數， 勢能在三階后被截斷， ?因此VMCSCF計算多達四重激發 ?［22］. 一般量子化學方法只考慮一重和二重這兩種主要激發， 其中雙重激發最為重要， 對相關能的校正起很大作用， 單激發對能量的校正遠遠小于雙激發， 而VMCSCF計算多達四重激發， 計算精度更高， ?VMRCI計算同樣多達四重激發， VMCSCF、VMRCI方法考慮了振動狀態間的靜態和動態相關效應， 最終實現對于體系振動能量的精確計算.

3 結果與討論

3.1 平衡幾何參數和勢能面

HCP是閉殼線性分子， 屬于 C ??∞ ??v 點群對稱， 非阿貝爾點群， 因此選取其子群 C ??2 ??v 方便展開計算， ??C ??2 ??v 點群的不可約表示為A ?1、B ?1、B ?2和A ?2， 分別對應對稱性為Σ、Σ、П和Π.

量化計算前首先進行幾何結構優化， HCP的幾何結構參數包括C-H鍵長、C-P鍵長以及HCP鍵角， 最低能量狀態下HCP保持線性狀態， 鍵角始終呈180°.在CCSD/cc-pVQZ方法下， 優化后的C-H鍵長為1.0698 ， C-P鍵長為1.5367 ， 而CCSD/cc-pVDZ方法下優化后的C-H鍵長為1.0865 ， C-P鍵長為1.5615 . 相比于實驗值 ?r （CH）=1.0670 和 r （CP）=1.5420?［28］， 明顯cc-pVQZ基組下的優化結果更加接近實驗值. 同基組不同方法下， HF/cc-pVQZ優化后的鍵長為 ?r （CH）=1.0611 和 r （CP）=1.5095?［28］， 對比實驗值可以發現相差較大， 仍然是CCSD/cc-pVQZ方法下的優化結果最接近實驗值， 其中， C-H鍵長與實驗值差0.0028 ， C-P鍵長與實驗值差0.0053 ， 鍵角也非常符合.

在CCSD/cc-pVQZ理論水平上優化過幾何平衡結構后， 在同一理論水平上確定了勢能面的擴展和法坐標. 線性分子的振動自由度為3 n -5（ n 為原子數）， 因此， 作為線性三原子分子， HCP具有四個振動自由度， 即振動模式的數量. 如圖1所示， HCP分子有四種正則振動模式， 分別為H-C拉伸振動、C-P拉伸振動、面內彎曲振動和面外彎曲振動. 在法向坐標中， 基本假設每種振動模式是相互獨立的.

圖2顯示了四種振動模式下的一維勢能曲線圖， 其中簡正坐標 q ??1、 q ??2分別對應HCP分子面內和面外彎曲振動模式， ??q ??3、 q ??4分別對應C-P鍵拉伸振動模式和H-C鍵拉伸振動模式. 從圖2a中可以看到， HCP面內彎曲振動模式的勢能曲線呈“U”型， 圖象關于 q ??1=0呈現出明顯的軸對稱特性， 其原因是HCP分子在面內彎曲振動模式下， 簡正坐標互為相反數的兩個振動狀態經過180°面外旋轉后重合， 對應的分子形狀本質上是相同的， 勢能相等， 故而勢能曲線對稱. ?另外， 圖2a和圖2b的勢能曲線圖是一樣的， 這是因為HCP分子的面內彎曲振動模式和面外彎曲振動模式在90°旋轉后實際上是相同的. 而在C-P和H-C拉伸振動模式下， 簡正坐標互為相反數時對應著不同的分子形狀， 勢能不同， 因此勢能曲線不再對稱， 如圖2c和圖2d所示. 特別是 q ??4坐標下勢能曲線明顯不對稱， 且曲線隨坐標變化更加陡峭， 這表明H-C拉伸振動模式在四種振動模式中對HCP分子體系振動勢能影響最大. 在分子的相關計算中， 適當利用相應的對稱性可以節省大量的計算時間和計算資源.

二維勢能面描述了HCP分子在不同的坐標組合下勢能變化的圖象， 其中二維相對勢能面如圖3所示， 由于彎曲振動在簡正坐標互為相反數時對應的分子形狀相同， 因而圖中含有 q ??1或 q ??2坐標的勢能面均呈現出對稱性. 如圖3a所示， 勢能面沿 q ??1和 q ??2坐標延伸， 由于面內、面外彎曲振動模式旋轉后重合， 因此圖象關于 q ??1 = 0和 q ??2 = 0同時呈現對稱性， 并且在這兩條線上勢能為零， 分子處于平衡狀態， 隨著坐標變化勢能面均勻向外延伸， 最終勢能面四角出現四個勢壘， 中心呈洼地狀. 類似地， 可以預測以 q ??1、 q ??3為坐標和以 q ??2、 q ??3為坐標的勢能面也應該是相同的. 結果確實如此， 并且圖象分別關于 q ??1 ??= 0和 q ??2 ??= 0對稱， 勢能面整體穩定， 分子基本處于平衡狀態. 圖3d與圖3e也是相同的， 相較其他坐標下的二維相對勢能面更加平穩， 只有當 q ??1、 q ??2坐標值很大時， 勢能才逐漸降低. ?q ??3、 q ??4坐標下的勢能面形狀較其他勢能面相比存在較大差異， 不再呈現對稱性， 而是在兩坐標值增大、減小時呈現出不同的勢能變化規律. 這是因為C-P鍵拉伸振動模式和C-H鍵拉伸振動模式振動頻率較大， 對分子體系的平衡狀態有較大影響.

圖4a展示了HCP分子在面內彎曲振動模態（ q ??1）與面外彎曲振動模態（ q ??2）耦合下的二維完整勢能面. ?q ??1、 q ??3坐標下和 q ??2、 q ??3坐標下的完整勢能面圖象與之相同， 圖上無明顯相變點， 整體呈“凹”狀， 四角處呈現高勢能， 中心處呈低洼狀， 在零坐標處出現全局極小值點， 勢能對坐標一階導數為0， 對應著體系的平衡狀態， 由極小值點向各個方向勢能逐漸升高. 當 q ??4作為坐標時， 完整勢能面圖象發生變化， 如圖4b所示， 勢能面上出現了一個鞍點. 這是由于H-C伸縮振動模態對分子系統的影響較大， 它通過影響HCP彎曲振動模式與C-P拉伸振動模式之間的耦合而影響體系勢能.

3.2 振動能級和振動光譜

在量化計算之前， 首先確定分子振動自由度， 即振動基頻的數目. 振動能級一般可表示為

E ?vib=∑ ?i=1 ??v ??i+ ?d ??i 2 ?h v ??i ?（3）

其中， ?d ?i 表示模式 i 的簡并度. HCP為線型分子， 具有四個振動自由度， 即四個基頻， 其振動動力學標記為（ v ??1， ?v ??2， ?v ??3， ?v ??4）. 由于HCP分子是線性分子， 振動能級間存在簡并現象， 如表1中所示， ?v ??1和 v ??2模式對應的振動頻率始終相同， 存在簡并現象. 這一現象也反映在隨后列舉的的倍頻和組合頻中.

由表1可以發現， C-P伸縮振動的基頻（ v ??3 = 1239.79 cm ?-1）與HCP彎曲振動的倍頻（2 v ??2 = 1398.12 cm ?-1）頻率接近， 產生了2∶1的費米共振， 從而使得對應頻率附近的吸收強度大大增強. 因此， 采用VMCSCF和VMRCI方法來計算具有共振現象的HCP分子體系是非常合理的. 通過對比表1中的數據可以發現， 相比于振動組態相互作用方法（VCI）， VMRCI方法計算出的振動頻率更接近實驗值， 計算精度也更高. 此外， 在四個基頻中， ?v ??4模式對應的H-C拉伸振動頻率最大， 對HCP分子的振動狀態影響也最大.

VMRCI/cc-pVQZ方法下的HCP分子振動基頻、倍頻和組合頻列于表2中， 同時列出的還有紅外和拉曼振動強度. 可以發現， HCP分子紅外活性和拉曼活性遵循互斥法則， 另外， 較高的振動強度都出現在基頻處， 說明基頻躍遷的能量更大. 同時， 本文的計算較精確， 即使一些強度較弱的振動也沒有被忽視. 基于強度和頻率數據， 可以進一步擬合繪制出HCP分子的光譜圖象， 紅外光譜圖和拉曼光譜圖分別如圖5和圖6所示.

根據表2中的數據， 振動強度最高的頻帶對應的頻率為684.34 cm ?-1， 強度值為65.93 km/mol， 對應HCP彎曲振動的基本躍遷. 然而， 在 圖5紅外光譜圖中最強吸收峰處的峰值強度卻為131.86 km/mol. 這是由于同一峰位處的兩個峰強度發生了疊加現象. 這是光譜圖的一個特點. 另一較強的譜帶出現在3242.61 cm ?-1頻率處， 對應C-P拉伸振動的基本躍遷， 對應紅外光譜圖上次高的峰. 這兩個峰是HCP分子紅外光譜圖的兩個主要特征峰. 此外， 一些強度較小的峰位在光譜圖上是不明顯的， 如3880.41 cm ?-1處和4620.81 cm ?-1處的兩個峰， 其強度分別為2.62 km/mol和1.54 km/mol， 但放大后清晰可見這些峰的存在. 這也可以與計算出的紅外強度值進行比對， 從而證明本文計算出的光譜數據是豐富和細致的.

從圖6可以看出， 拉曼光譜也有兩個主要特征峰， 分別位于3242.61 cm ??-1和1239.79 cm ?-1處， 對一些弱峰進行放大可以清晰可見其峰位和峰強. 對比圖5和圖6可以發現， HCP分子的紅外和拉曼活性不在同一振動頻率下出現， 遵循互斥法則. 這兩者計算出來之后相互補充， 共同構成HCP分子的詳細光譜. 與紅外光譜不同的是， 拉曼光譜信號較弱， 一般在實驗中更難測量到. 但同時它又對分子振動分析有著重要意義， 因此本文關于拉曼光譜的計算為HCP分子光譜研究提供了參考數據.

4 結 論

本文基于Molpro程序包， 采用從頭算方法對HCP分子勢能面和振動光譜進行了研究. 首先， 采用cc-pVQZ/CCSD方法對HCP分子幾何結構進行優化. 優化后的C-H鍵長和C-P鍵長與實驗值非常接近. 計算得到了HCP分子豐富的一維勢能曲線、二維相對勢能面和二維完整勢能面. 其中， H-C伸縮振動模式通過影響HCP彎曲振動模式和CP拉伸振動模式之間的耦合來影響分子體系的勢能， 導致完整勢能面中出現了鞍點. 基于勢能面， 采用VMCSCF、VMRCI從頭算方法對具有費米共振現象的CP分子振動能級和振動光譜展開計算. 發現了振動能級中的簡并現象以及CP伸縮振動模式與HCP彎曲振動模式之間的費米共振現象. 該方法計算出的振動頻率與實驗值相吻合， 且更加接近實驗值. 進一步繪制出的光譜圖象為HCP分子光譜研究提供了參考數據. 本文整體工作對于HCP等含磷分子的實驗和后續理論工作具有參考作用.

參考文獻：

［1］ ??Gier T E. HCP， a unique phosphorus compound ［J］. J Am Chem Soc， 1961， 83： 1769.

［2］ ?Garneau J M， Cabana A. The ν ?1 and ν ?1 + ν ?2 - ν ?2 infrared absorption bands of H ?12CP ［J］. J Mol Spectrosc， 1978， 69： 319.

［3］ ?Garneau J M， Cabona A. High-resolution infrared absorption spectrum of H ?12CP. The ν ?3 band ［J］. J Mol Spectrosc， 1980， 79： 502.

［4］ ?Garneau J M， Cabana A. The vibration-rotation spectrum of methinophosphide： l-type doubling， l-type resonance and the ν ?2， 2ν ?2， and 3ν ?2 bands of H ?12CP; the ν ?1 and ν ?2 bands of H ?13CP ［J］. J Mol Spectrosc， 1981， 87： 490.

［5］ ?Cabana A， Doucet Y， Garneau J M， ?et al. ?The vibration-rotation spectrum of methinophosphide： ?the overtone bands 2ν ?1 and 2ν ?3， the summation bands ν ?1 + ?ν ?2 and ν ?2 + ν ?3， and the difference band ν ?1 - ν ?2 ??［J］. J Mol Spectrosc， 1982， 96： 342.

［6］ ?Agúndez M， Cernicharo J， Guélin M. Discovery of phosphaethyne（HCP）in space： phosphorus chemistry in circumstellar envelopes ［J］. Astrophys J， 2007， 662： L91.

［7］ ?Bera P P， Yamaguchi Y， Schaefer III H F. Low-lying quartet electronic states of nitrogen dioxide ［J］. J Chem Phys， 2007， 127： 174303.

［8］ ?Yu Q， Bowman J. Communication： VSCF/VCI vibrational spectroscopy of H ?7O ?3 ?+ and H ?9O ?4 ?+ using high-level， many-body potential energy surface and dipole moment surfaces ［J］. J Chem Phys， 2017， 146： 121102.

［9］ ?Meier P， Oschetzki D， Pfeiffer F， ?et al. ?Towards an automated and efficient calculation of resonating vibrational states based on state-averaged multiconfigurational approaches ［J］. J Chem Phys， 2015， 143： 244111.

［10］ ?Transue W J， Velian A， Nava M， ?et al. ?A molecular precursor to phosphaethyne and its application in synthesis of the aromatic 1， 2， 3， 4-phosphatriazolate anion ［J］. J Am Chem Soc， 2016， 138： 6731.

［11］ Chen Y T， Chong D P. Comparison of theoretical vibrational and rotational energies of the HCP molecule with experimental values ［J］. J Chem Phys， 1993， 99： 8870.

［12］ Koput J. The equilibrium structure and spectroscopic constants of HCP-an ?ab initio ?study ［J］. Chem Phys Lett， 1996， 263： 401.

［13］ Koput J， Carter S. The potential energy surface and vibrational-rotational energy levels of HCP ［J］. Spectrochim Acta A， 1997， 53： 1091.

［14］ Beck C， Schinke R， Koput J. Vibrational spectroscopy of phosphaethyne（HCP）. I. Potential energy surface， variational calculations， and comparison with experimental data ［J］. J Chem Phys， 2000， 112： 8446.

［15］ H ltzl T， Szieberth D， Nguyen M， ?et al. ?Formation of phosphaethyne dimers： a mechanistic study ［J］. Chem Eur J， 2006， 12： 8044.

［16］ Wang A， Sun L， Fang C， ?et al. ?Study of highly excited vibrational dynamics of HCP integrable system with dynamic potential methods ［J］. Chin Phys B， 2020， 29： 013101.

［17］ Wang A， Sun L， Fang C， ?et al. ?The study of dynamic potentials of highly excited vibrational states of DCP： from case analysis to comparative study with HCP ［J］. Int J Mol Sci， 2016， 17： 1280.

［18］ Loos P F， Scemama A， Boggio-Pasqua M， ?et al. ?Mountaineering strategy to excited states： highly accurate energies and benchmarks for exotic molecules and radicals ［J］. J Chem Theory Comput， 2020， 16： 3720.

［19］ 張學富， 呂兵， 宋曉書， 等. BeH分子基態振動能級與光譜常數的理論研究［J］. 四川大學學報： 自然科學版， 2018， 55： 533.

［20］ 萬沖， 宋曉書， 呂兵， 等. CaH分子低激發態的勢能曲線和光譜性質［J］. 四川大學學報： 自然科學版， 2020， 57： 315.

［21］ 雷良建， 萬沖， 王興煒， 等. NH自由基基態及低激發態從頭計算研究［J］. 四川大學學報： 自然科學版， 2020， 57： 953.

［22］ Pfeiffer F， Rauhut G. Multi-reference vibration correlation methods ［J］. J Chem Phys， 2014， 140： 064110.

［23］ Albuquerque J V， Shirsat R N. Prelude to molecular dynamics-II： investigation of potential energy surfaces using gaussian charge models ［J］. Chem Sel， 2020， 5： 11052.

［24］ Barreto P R P， Cruz A C P S， Euclides H O， ?et al. ?Spherical harmonics representation of the potential energy surface for the H ?2…H ?2 van der Waals complex ［J］. J Mol Model， 2020， 26： 277.

［25］ Melchakova I， Nikolaeva K M， Kovaleva E A， ?et al. ?Potential energy surfaces of adsorption and migration of transition metal atoms on nanoporus materials： the case of nanoporus bigraphene and G-C ?3N ?4［J］. Appl Surf Sci， 2021， 540： 148223.

［26］ Zhang K， Yin L， Liu G. Physically inspired atom-centered symmetry functions for the construction of high dimensional neural network potential energy surfaces ［J］. Comput Mater Sci， 2021， 186： 110071.

［27］ Qian W， Lu B， Tan G， ?et al. ?Vibrational spectrum and photochemistry of phosphaketene HPCO ［J］. Phys Chem Chem Phys， 2021， 23： 19237.

［28］ NIST. Computational chemistry comparison and benchmark DataBase ［DB/OL］. ［2022-05-22］. https：//cccbdb.nist.gov/.