一種基于MLP-ELM的GaN HEMT 小信號特性的建模方法

程旭瀚 王軍

摘 要 ???：本文提出了一種基于MLP-ELM的GaN HEMT小信號特性的建模方法，首先基于GWO建立了一種混合參數提取法，解決20元等效電路參數提取不精確的問題;然后利用等效電路模型獲得的S參數結合MLP-ELM建立了一種精確的經驗模型，有效解決等效電路模型無法在多偏置范圍內表征小信號特性的問題;最后利用MLP-ELM建立了一種基于經驗的小信號模型.經過仿真分析得出，本文所建模型精度高，在整個偏置范圍內有效且具備等效電路模型不具有的泛化能力.

關鍵詞 ：等效電路模型； 灰狼優化算法； S參數； 多層感知器； 極限學習機

中圖分類號 ：TN386 文獻標識碼 ：A DOI ： ?10.19907/j.0490-6756.2023.044003

收稿日期： ?2022-11-08

基金項目： ?國家自然科學基金（69901003）; 四川省教育廳科研基金（18ZA0502）

作者簡介： ??程旭瀚（1996-）， 男， 研究方向為微波器件建模及應用. E-mail： chengxh702020@163.com

通訊作者： ?王軍. E-mail： wangjun197008@163.com

An MLP-ELM-based modeling method for the ?small-signal properties of GaN HEMT

CHENG Xu-Han， WANG Jun

（Southwest University of Science and Technology College of Information Engineering， Mianyang 621010， China）

An MLP-ELM-based modeling method for GaN HEMT small-signal properties is proposed. First， a hybrid parameter extraction method is developed based on the GWO to solve the problem of inaccurate extraction of 20-element equivalent circuit parameters; then the S-parameters obtained from the model are combined with MLP-ELM to establish an accurate empirical model， which effectively solves the problem that the equivalent circuit model cannot represent the small signal properties in the multi-bias range; finally， an empirical-based small signal model is developed with MLP-ELM. The simulation results show that the proposed model has high precision， is effective in the whole bias range and has the generalization ability that the equivalent circuit model lacks.

Equivalent circuit model; Gray wolf optimization algorithm; Scattering parameters; Multilayer perceptron; Extreme learning machine

1 引 言 GaN HEMT具有高電子飽和速度和寬帶隙等特點，廣泛應用于如功率放大器和低噪聲放大器等電路模塊.設計這些模塊需要可靠、準確的小信號特性建模方法，常用的方法是等效電路模型. 該模型的準確性依賴于模型拓撲與參數提取的方法 ?［1-3］.由于20元等效電路結構復雜，直接提取法并不適用，因此基于優化的提取過程是非常必要的 ?［2，3］.這種將優化方法與直接提取法相結合的方法被稱為混合參數提取法.在模型優化問題上群智能算法是可行且有效的 ?［4］. 針對器件建模問題，研究者基于群智能算法提出了眾多的混合參數提取法 ?［5-7］，其中灰狼優化算法（Gray Wolf Optimization，GWO）具備魯棒性強和結構簡單等特點 ?［8］，廣泛應用于器件建模 ?［5］和人工神經網絡（Artificial Neural Network，ANN）優化等場景 ?［9］.因此本文基于GWO解決20元等效電路參數提取不精確的問題.

基于知識（等效電路模型、經驗模型等）的ANN建模方法備受關注 ?［10，11］. 常用的ANN模型為多層感知器（Multilayer Perceptron， MLP） ?［11，12］， 但該模型的準確性與泛化能力依賴于網絡結構 ?［13］. 因此本文基于GWO明確MLP的最優網絡結構.由于極限學習機（Extreme Learning Machine，ELM）具備的快速訓練優勢 ?［14］， 本文建立一種基于MLP-ELM表征小信號特性的方法. 該方法通過ELM進一步提高MLP模型的精度與泛化能力. 由于將等效電路模型作為先驗知識的方法會缺失部分偏置點的信息 ?［11］，因此將等效電路模型獲得的 S 參數結合MLP-ELM建立一種與偏置相關的經驗模型. 該模型能準確地表征所有偏置條件下的等效電路 S 參數， 然后建立一種基于經驗的MLP-ELM模型.該模型能在全偏置范圍內準確表征小信號特性，并具備等效電路模型不具有的泛化能力.

本文基于MLP-ELM建立一種GaN HEMT小信號模型，實驗數據的來源是廠商提供的ADS模型. 最后，通過不同模型的 S 參數對比分析， 說明本文方法的有效性和實用性.

2 ?基于GWO的20元等效電路建模流程

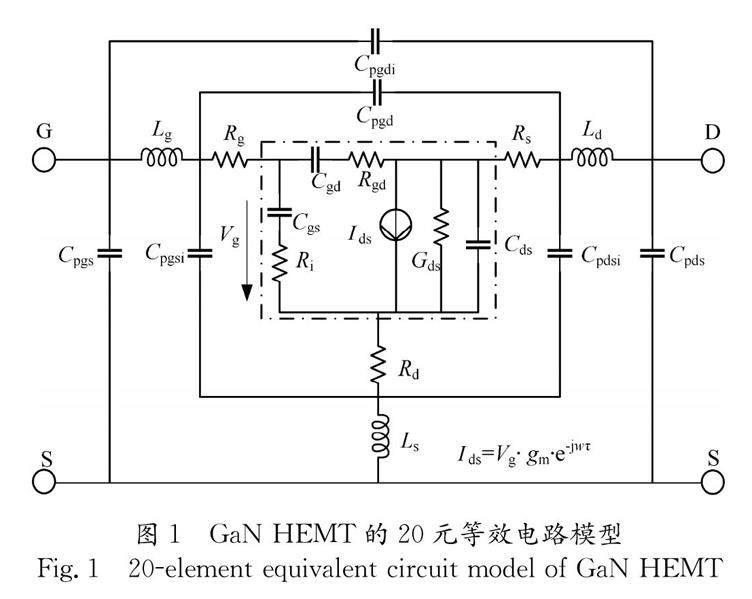
本文采用圖1所示的20元等效電路模型作為GaN HEMT的小信號模型，其中虛線框內的為本征部分，其余部分為寄生部分. 該模型的寄生部分參數是偏置無關的，它們分別為考慮了襯墊連接的電容 C ??pgs、 C ??pds和 C ??pgd，考慮了柵極、漏極和源極空氣橋連接所引入的電容 C ??pgsi、 C ??pdsi和 C ??pgdi，模擬金屬化電感的 L ??g、 L ??s和 L ??d，由于接觸等引起的電阻 R ??g、 R ??d和 R ??s;本征部分的參數是偏置相關的，它們分別為柵極和2DEG溝道電荷形成的平行板電容 C ??gd和 C ??gs，漏極和源極之間的交疊電容 C ??ds，分布溝道電阻 R ??i和 R ??gd，溝道電阻 R ??ds（1/ G ??ds），柵極與漏極之間的直流跨導 g ??m和信號傳輸時間延遲常數 τ .

本文選取低頻條件下（ f <0.5 GHz）的“Cold-pinch”（ V ??DS=0 V， V ??GS< V ??T）條件對寄生電容進行提取. 這種情況下的電路拓撲等效為Π型網絡 ?［3］. 將該偏置點下的 S 參數轉為 Y 參數，根據二端口網絡可得柵源端的支路總電容 C ??gso、柵漏端總電容 C ??gdo與源漏端總電容 C ??dso. 其中， 柵源端的支路總電容 C ??gso為 C ??pgs、 C ??pgsi與 C ??gs的電容之和， 同理可得 C ??gdo與 C ??dso. 在高頻的零偏條件下（ V ??GS=0 V， V ??DS=0 V），將外圍的寄生電容 C ??pgs、 C ??pgd和 C ??pds去嵌后，20元等效電路模型等同于T型網絡 ?［3］. 將該偏置點下的 S 參數轉為 Z 參數，根據二端口網絡得到寄生電感、寄生電阻與 Z 參數的關系 ?［3］，根據線性擬合提取相關參數值. 由于圖1的寄生電容個數過多，因此需要額外的關系才能求解.采用文獻［15］設定電容值的經驗關系.

C ??pgs= C ??pds

C ??pgdi=2 C ??pgd

C ??gs= C ??gd

C ??pdsi=3 C ??pgs ?（1）

由上述所知，通過遍歷不同的 C ??pgs與 C ??p ?gd的值 ?［15］（ C ??pgs從0到0.5 C ??dso， C ??p ?gd從0到0.5 C ??gdo），再結合寄生電感與寄生電阻的提取方法得到不同 C ??pgs與 C ??p ?g ?d條件下的所有寄生參數值. 根據誤差公式將最小誤差下的值作為寄生參數優化算法的初始值. 誤差公式為 ?［15］

（2）

其中，

（3）

W ?ij= ?max （|S ??mea ??12|，|S ??mea ??12|）， i，j=1，2;i≠j

1+|S ??mea ??ii|， i=1，2 ??（4）

其中， ||·|| ?1表示矩陣的1范數; ?N 表示實驗數據總數; Δ S 表示 S 參數實驗值（上標為mea）與 S 參數仿真值（上標為sim）之間的差值. 由于式 （1）～（4）的經驗等式和電路拓撲等導致存在誤差，需要優化算法減小誤差. 本文采用GWO進行參數優化. 這里簡要闡述該算法的原理： 它模擬了灰狼物種的領導階層 ?［8］，其中 α 、 β 和 δ 狼是解決方案優于其他狼（ ω ）的領導者，它們的位置向量（ X ?α 、 X ?β 和 X ?δ ）用于更新其他狼的位置向量的方法如下所示 ?［8］.

X 1（t）-X α（t）-A 1|CX α（t）-X（t）|

X 2（t）-X β（t）-A 2|CX β（t）-X（t）|

X 3（t）-X δ（t）-A 3|CX δ（t）-X（t）| ??（5）

A=2a·r 1-a ?（6）

C=2·r 2 ?（7）

X（t+1）= X 1（t）+X 2（t）+X 3（t） 3 ??（8）

其中， 表征狼的位置向量為 X =［ x ??1， x ??2，… x ?n ］ ?T; ?n 表示優化問題的維度; ?r ??1和 r ??2為［0，1］中的隨機向量; ?t 為當前迭代次數; 參數 A ??1、 A ??2和 A ??3由公式（6）得到. 由于電容之間存在約束條件（各個支路總電容），因此對寄生參數 C ??pgs、 C ??pds、 C ??pgd、 C ??pgsi、 C ??pgdi、 C ??pdsi、 L ??s、 L ??d、 L ??g、 R ??s、 R ??d和 R ??g進行優化（ n =12）. 其中基于GWO的優化算法的適應性函數為

E S= 1 N ∑ 2 ?i=1，2 ∑ 2 ?j=1，2 ∑ 2 ?n=1 ??S ?mea ??ij，n-S ?sim ??ij，n ??S ?mea ??ij，n ????（9）

群體智能算法需要一種初始化策略生成初始種群， 而一個好的初始種群會影響尋優過程的收斂速度與最終解的精度. 由于GWO的最終優化值的精度依賴于初始狼群的位置，而初始狼群位置的生成依賴于直接提取法得到的初始值，因此本文采用迭代的思路將GWO產生的最終值作為下一次GWO初始狼群位置的依據. 這種方法稱為基于迭代的灰狼優化算法（I-GWO）. 最終寄生參數的提取流程如圖2所示.

在寄生參數優化過程中，采用一次迭代的GWO方法，其中狼群數目 W ?N 為15， 最大迭代次數 Max ?iter 為100.明確最小|??S|條件下的 C ??pgs與 C ??p ?gd的初始值后便可以計算其他寄生參數值并進行優化算法的流程. 最終得到的寄生參數初始值與優化值如表1所示.

本征參數與偏置電壓有關，一般通過 S-Y-Z 的參數轉換，逐步剝離寄生參數的影響 ?［2］得到本征參數，并根據文獻［3］可得本征參數的計算公式. 本文采用直接提取法得到的重要本征參數的初始值與偏置 V ??GS和 V ??DS的關系如圖3所示. 其中 V ??GS的范圍是-4～0 V，間隔0.5 V; V ??DS的范圍是從 0～28 V，間隔1 V.

由圖3可知，在 V ??DS恒定的情況下，當 V ??GS向夾斷區移動時， C ??gs值下降;當 V ??GS接近0 V時， C ??gs顯著增加. 在恒定的 V ??GS條件下，由于漏極處的正電荷阻礙了電容效應 ?［16］，電容 C ??gd隨著V ?DS的增加而降低. ?g ?m 的非對稱鐘形是GaN HEMT的一個眾所周知的特征 ?［15，16］. 在低 V ??DS區域，可以觀察到電容 C ??ds為負值. ?這種情況同樣出現在文獻［2，16］的結果中. 上述的結果表明， 本文所提的本征參數初始值具有物理意義，為后續的優化提供良好的起點.

圖4a為針對寄生參數優化問題采用傳統GWO與I-GWO所得的 E ??s與迭代次數的關系. 由圖可以明顯地看出， I-GWO較傳統GWO能顯著地降低電容經驗關系導致的模型誤差; 在時間成本相似的情況下（傳統GWO的平均時間為49.3 s，I-GWO的平均時間為48.9 s），相同的迭代次數I-GWO優化的效果明顯好于傳統GWO. 由于本征參數與頻率存在的相關性導致一定的誤差 ?［15］，因此采用I-GWO進一步提高本征參數的精度. 具體流程與圖2的參數優化部分類似，其中優化的對象為本征參數 C ??gs、 C ??gd、 C ??d ?s、 R ??i、 R ??gd、 g ??m、 g ??ds與 τ （ n =8）. 采用一次迭代的GWO的方法，其中狼群數目 W ?N 為15， 最大迭代次數 Max ?iter 為200. 本文以 V ??GS= -3 V， V ??DS從2到4 V，間隔1 V的偏置條件為例，得到不同偏置條件下適應性函數 E ??s與迭代的關系，如圖4b所示. 其中區域1為第一次GWO的 E ??s與迭代次數的關系，區域2為第二次GWO的 E ??s與迭代次數的關系. 由圖4b可知，只用一次GWO的情況下，各個狼群位置可能難以擺脫當前位置而陷入局部最優; 通過第二次GWO生成隨機的初始狼群位置的方法，使其可能逃離局部最優點. 上述說明了I-GWO提升了參數優化問題的能力. 文獻［5］使用傳統GWO對寄生參數值進行優化并采用直接提取法得到本征參數值. 該方法未考慮本征參數的頻率依賴性導致的模型誤差，而圖4b說明了直接提取法所得模型的誤差較高（迭代次數為0時的 E ??s）. 本文采用I-GWO優化本征參數值可以明顯減少上述誤差，同時說明I-GWO在優化寄生參數能力上優于傳統GWO. 上述驗證了本文所提的I-GWO在等效電路建模場合的有效性與實用性.

3 ?等效電路模型結合MLP-ELM的建模流程

高精度的等效電路模型能更好地表征所提偏置點下的 S 參數特性. 但等效電路模型是單偏置相關的 ?［11］，將等效電路模型作為先驗知識會缺失其他提取的偏置點信息. 因此將20元等效電路模型的 S 參數作為訓練數據，基于MLP-ELM訓練并產生與偏置相關的經驗模型，如圖5所示. MLP部分由輸入層、輸出層以及 m 個隱藏層組成 ?［12］.文中的MLP模型的輸入為 V ??GS、 V ??DS與頻率 f ，輸出為4個 S 參數，其中每個 S 參數用實部與虛部表示. ELM模型在結構上是單隱藏層的MLP ?［14］，其作用是優化MLP的輸出，因此輸入層與輸出層的個數均為8. MLP與ELM模型的區別在于訓練的過程. MLP訓練的是隱藏層與輸入層、隱藏層與隱藏層以及輸出層與隱藏層的連接權重；而ELM只訓練輸出層與隱藏層的連接權重. 設定隱藏層的激活函數為式（10）所示的雙曲正切函數，輸出層的激活函數為式（11）所示的線性函數.

f（x）= ?e ?x- e ??-x ?e ?x+ e ??-x ??（10）

f（x）=x ?（11）

本文采用分階段訓練ANN的方式，先建立最優MLP模型，再根據最優MLP建立最優ELM模型. 因此本質上MLP與MLP-ELM模型是分離的. 本文基于GWO尋找MLP的最優網絡結構，包括隱藏層個數 m 與各個隱藏層神經元個數 h ??1， h ??2，…， h ?m ，并通過遍歷隱藏層的方法得到ELM的最優隱藏層神經元個數 N ??ELM. 定義以下目標函數來評估MLP模型的準確性與泛化能力 ?［13］.

F=（E ??train +E ??test ）·K ?（12）

其中， E ??train為訓練誤差; E ??test為泛化誤差. 用相對誤差絕對值的平均值計算 E ??train和 E ??test.

E ?train= 1 N ?train ∑ ?N ?train ?i=1 ??Y ?pre ?i-Y ?train ?i Y ?train ?i ???（13）

E ?test= 1 N ?test ∑ ?N ?test ?i=1 ??Y ?pre ?i-Y ?test ?i Y ?test ?i ???（14）

其中， N ??train為訓練數據個數; ?N ??test為測試數據個數;上標pre的參數為模型的預測值;上標train和test分別表示訓練集和測試集的實驗值. 對于具有較低 E ??train的MLP模型，可能存在預測值與目標值相差甚遠的情況. 因此式（12）中的懲罰因素 K 的計算方法為 ?［13］

K=1+0.33N ??avg +N ??bad ??（15）

其中， N ??avg是相對誤差0.15～0.25的測試集的數量; ?N ??bad是相對誤差高于0.25的測試集的數量 ?［13］. MLP與ELM模型的訓練環境為MATLAB 2017b，CPU為AMD-4800H，運行內存為16 GB. 在訓練之前，需要將數據進行歸一化處理. 該方式有利于ANN的訓練 ?［12］. 訓練數據與測試數據均來自于20元等效電路模型生成的 S 參數. 其中 V ??GS的范圍為-4～0 V，間隔0.5 V，共計9個偏置點; V ??DS的范圍為0～28 V，間隔1 V，共計29個偏置點;頻率的范圍為0.1～6 GHz，間隔0.1 GHz，共計60個頻率點;每一個 V ??GS偏置值下共下有29個 V ??DS的偏置點. 這樣組成的（ V ??GS， ?V ??DS）偏置條件下共有60個頻率點下的 S 參數，因此用于訓練的數據共計15 660組. 將80%的數據作為訓練集，20%的數據作為測試集.

由于優化的是MLP結構，因此數值必須保證為整數. 本文的MLP的隱藏層層數 k 約束為3層，每一層的神經元個數的下界約束 lb 為（1，1，1），上界約束 ub 為（20，20，20）. 根據約束條件隨機生成灰狼的初始位置，每一個灰狼的初始位置代表著不同結構的MLP模型，并為這些模型分配不同的訓練集與測試集. 最后將最小F下的灰狼位置作為MLP的最優結構. 其中GWO參數的設定是：狼群數目 W ?N 為15，最大迭代次數 Max ?iter 為15.

保持訓練集與測試集一致的情況下，將最優結構的MLP模型的輸出作為ELM模型的輸入，通過ELM模型進一步提高MLP模型的精度與泛化能力. ELM的具體原理如文獻［14］所述. 由于ELM的精度與泛化能力受隱藏層神經元個數 N ??ELM影響，因此本文根據步長 N ??step與最大上限 N ??max遍歷ELM的隱藏層個數，通過判斷訓練集與測試集的均方誤差（ MSE ）確定ELM的最優結構. ?MSE 的計算式為

MSE= 1 M ∑ M ?i=1 ??Y ?i-Y ?pre ?i ?2 ?（16）

其中 M 為訓練集或測試集的樣本個數， Y ?i 為訓練集或測試集的實驗值.圖6為等效電路模型結合MLP-ELM的建模流程圖，其中包括基于GWO的MLP結構優化流程與ELM的最優隱藏層遍歷流程.

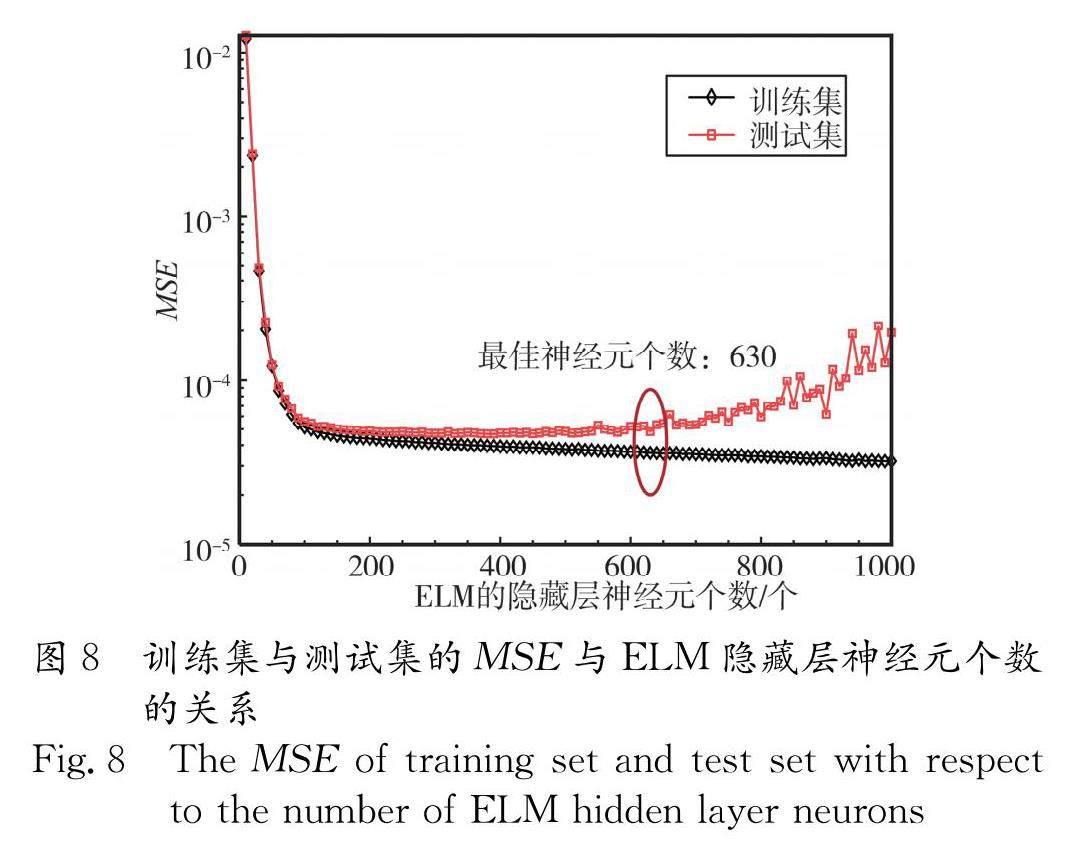
設定 N ??step為10， N ??ELM的起始點為10， N ??max為1000，根據圖6所示的流程得到評估MLP模型精度與泛化能力的 F 與迭代次數的關系，如圖7所示. 由圖7可以看到， F 最終收斂到較低的值，因此得到MLP的最優神經網絡結構為3-13-13-19-8. 圖8所示的是訓練集與測試集的均方誤差 MSE 與ELM隱藏層個數的關系. 通過分析可得， 隨著隱藏層個數的遞增，訓練集的 MSE 遞減而測試集的 MSE 先快速遞減然后保持一定的收斂趨勢，最后呈現上升的趨勢. 這表明ELM模型的隱藏層個數會影響模型的精度與泛化能力. 因此根據測試集的 MSE 較低值確定ELM的最優隱藏層個數為630.

最終建立的經驗模型的數學表達式 S ??emp為

S ??emp =f ??ELM （S ??MLP ，w ??ELM ）

S ??MLP =f ??MLP （V ??GS ，V ??GS ，f，w ??MLP ） ??（17）

其中， w ??ELM為最優ELM的權重; ?w ??MLP為最優MLP的權重. ?S ??MLP為偏置相關的函數，因此經驗模型 S ??emp解決了等效電路模型無法在多偏置范圍內表征小信號特性的問題.

4 ?基于經驗模型的MLP-ELM建模流程

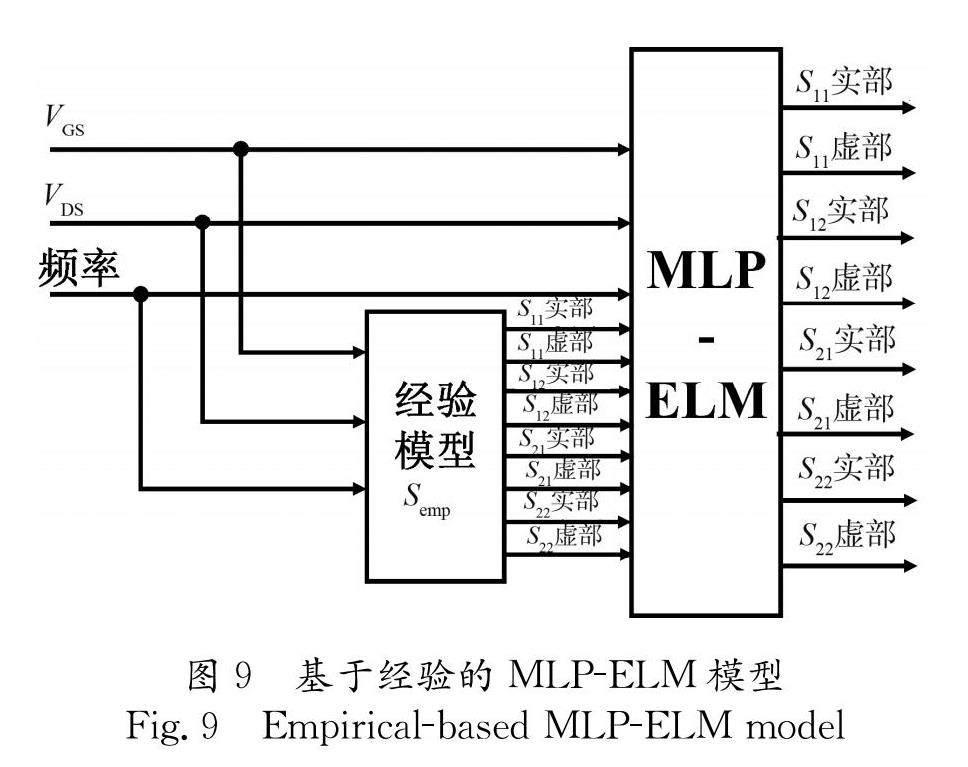
為表征GaN HEMT的小信號特性，本文將經驗模型作為先驗知識與MLP-ELM結合，建立一種基于經驗的MLP-ELM模型，如圖9所示. 該模型利用經驗模型提供的附加信息，提高模型的精度，并且在常用的MLP模型的基礎上通過ELM進一步提高模型的精度與泛化能力.

該模型包含的MLP-ELM模型的輸入為 V ??GS、 V ??DS、頻率 f 和 S ??emp，輸出為 S 參數的實部與虛部. 由于經驗模型 S ??emp能有效地表征等效電路模型的小信號特性，因此可以簡化MLP模型的復雜度，從而減小訓練時間. 基于GWO優化MLP最優結構的設定為：MLP的隱藏層層數約束為2層； lb 為（1，1）；上界約束 ub 為（20，20）；狼群數目 W ?N 為15；最大迭代次數 Max ?iter 為15. ELM的最優結構的遍歷方法與第三部分設定一致. 訓練MLP與ELM的訓練數據與測試數據結構與第三部分一致，但數據的來源為廠商提供的ADS模型，因此將圖6的20元等效電路模型的 S 參數替換為上述的數據，再根據圖6的流程可得MLP-ELM模型的結構. MLP模型的結構為11-14-16-8，ELM模型的結構為8-530-8.

5 實驗驗證與分析

根據本征參數優化方法得到如表2所示的在 V ??GS=-3 V， V ??DS=5 V的本征參數初始值與優化值.

根據圖1的20元等效電路模型，將表1的寄生參數優化值與表2的本征參數值帶入等效電路模型中，得到在頻率 f 范圍為0.1～6 GHz， V ??GS=-3 V， V ??DS=5 V偏置條件下的20元等效電路模型的 S 參數值，并將相同條件的（ V ??GS， V ??DS， ?f ?）帶入基于經驗的MLP-ELM模型，該模型得到的 S 參數值與實驗數據進行對比，如圖8a所示. 由圖可以明顯地看出，經過GWO參數優化后的20元等效電路能很好地表征GaN HEMT的小信號特性. 其中 S 參數的平均相對誤差為4.23%，滿足建模要求. 同時，基于經驗的MLP-ELM模型比等效電路模型的精度更高，說明了所提方法的有效性. 我們進一步分析MLP-ELM方法的有效性. 表3所示的是基于MLP-ELM的經驗模型在不同網絡搭建階段下，由等效電路模型獲得的 S 參數和實驗數據作為訓練集與測試集的 MSE . 由表3很明顯地看出，在MLP階段下的訓練集與測試集的MSE已滿足建模需求. 在ELM階段下訓練集與測試集的 MSE 較MLP階段得到優化， 這說明MLP-ELM模型的精度與泛化能力比MLP模型更好. 為說明MLP與ELM結合的必要性，使用等效電路模型獲得的 S 參數作為數據源，采用遍歷隱藏層的方式建立基于ELM的經驗模型. 最終得到的ELM結構為3-2700-8，其在訓練集的MSE與測試集的MSE分別為1.4923×10 ?-4和2.3273×10 ?-4. 這說明了該模型在訓練集與測試集的精度上遠低于MLP模型與MLP-ELM模型. 圖8b所示的是 V ??GS=-2 V， V ??DS=6 V的偏置條件下，基于MLP的經驗模型、基于ELM的經驗模型、基于MLP-ELM的經驗模型和20元等效電路模型的 S 參數對比圖. 由該圖可知， 基于MLP-ELM的方法比基于MLP和ELM的方法更能準確地表征等效電路的 S 參數，且基于MLP的方法在擬合程度上明顯優于基于ELM的方法. 這說明了針對 S 參數建模僅采用ELM結構是低精度的，而將ELM優化MLP模型則顯著提高精度. 這也表明了采用ELM優化MLP模型的可行性.

使用實驗數據作為數據源，采用遍歷隱藏層的方式建立基于經驗的ELM模型，則最終得到的ELM結構為11-2150-8. 其在訓練集與測試集的 MSE 分別為4.3232×10 ?-5和3.1189×10 ?-5，說明了該模型在訓練集與測試集的精度上遠低于MLP模型與MLP-ELM模型. 圖8c所示的是 V ??GS= -2.5 V， V ??DS=28 V的偏置條件下，基于經驗的MLP-ELM模型、基于經驗的MLP模型、基于經驗的ELM模型與實驗數據的 S 參數對比圖. 該偏置條件的實驗值不包含在訓練集與測試集之中. 分析可得，ELM-MLP模型較MLP和ELM模型具備更好的泛化能力，即該模型具備預測未測量偏置電壓 S 參數的良好能力. 上述分析表明，在基于相同經驗（基于MLP-ELM的經驗模型）的場合下ELM優化MLP模型的可行性. 因此，通過ELM優化MLP的方法可以較好地提高泛化能力.

上述結果表明，基于MLP-ELM的建模方法不僅適合數據驅動的場合，也適合基于經驗的場合，說明了本文方法的實用性.

6 總 結

本文提出了一種基于MLP-ELM的GaN HEMT小信號特性的建模方法，在建模過程中建立了三種模型. 第一個是20元等效電路模型. 該模型的精度通過混合參數提取法得到有效提高，建模的方法為復雜拓撲的參數提取提供了基礎. 第二個是基于MLP-ELM的經驗模型. 該模型有效解決等效電路模型無法在多偏置范圍內表征小信號特性的問題，并且驗證了通過ELM優化MLP模型的精度與泛化能力的有效性. 第三個是基于經驗的MLP-ELM模型. 該模型通過改進等效電路作為經驗模型的方法，最終準確的表征實際的GaN HEMT的小信號特性，并具備等效電路模型不具有的泛化能力. 因此，基于MLP-ELM的方法為后續建立微波晶體管小信號模型提供了基礎與經驗.

參考文獻：

［1］ ??王林， 王軍， 王丹丹. 40納米MOSFET毫米波等效電路的弱反區關鍵參數提取［J］. 四川大學學報： 自然科學版， 2017， 54： 523.

［2］ ?Poluri N， Desouza M M， Venkatesan N， et al . ?Modelling challenges for enabling high performance amplifiers in 5G/6G applications ［C］// 2021 28th International Conference on Mixed Design of Integrated Circuits and System. Lodz， Poland： Department of Microelectronics and Computer Science， Lodz University of Technology， 2021.

［3］ ?聞彰， 徐躍杭， 徐銳敏. 氮化鎵功率器件小信號模型參數提取算法研究［J］. 電波科學學報， 2015， 30： 772.

［4］ ?張慶華， 龍偉， 李炎炎， 等. 基于鯨魚算法優化LSSVM的銑刀磨損監測［J］. 四川大學學報： 自然科學版， 2022， 59： 012005.

［5］ ?Jarndal A. Graywolf optimization-based modeling technique applied to GaN high mobility electron transistors ［J］. IEEE J Electron Devi， 2021， 9： 968.

［6］ ?Hussein A S， Jarndal A H. Reliablehybrid small-signal modeling of GaN HEMTs based on particle-swarm-optimization ［J］. IEEE Trans Comput Aided Des Integrated Circ Syst， 2018， 37： 1816.

［7］ ?Zhang J， Hou X， Liu M， ?et al . Hybrid small-signal modeling of GaN HEMTs based on improved genetic algorithm ［J］. Microelectron J， 2022， 127： ?105513.

［8］ ?Mirjalili S， Mirjalili S M， Lewis A. Grey wolf optimizer ［J］. Adv Eng Softw， 2014， 69： 46.

［9］ ?Mirjalili S. How effective is the Grey Wolf optimizer in training multi-layer perceptrons ［J］. Appl Intell， 2015， 43： 150.

［10］ ?戚軍軍， 呂紅亮， 張玉明， 等. 基于人工神經網絡的有源器件建模概述［J］. 微納電子與智能制造， 2021， 3： 36.

［11］ Marinkovic Z， Pronic-Rancic O， Markovic V. Bias-dependent hybrid PKI empirical-neural model of microwave FETs ［J］. Int J Electron， 2011， 98： 1399.

［12］ Zhang Q J， Gupta K C， Devabhaktuni V K. Artificial neural networks for RF and microwave design-from theory to practice ［J］. IEEE T Microw Theory， 2003， 51： 1339.

［13］ Benardos P G， Vosniakos G C. Optimizing feedforward artificial neural network architecture ［J］. Eng Appl Artif Intel， 2007， 20： 365.

［14］ Huang G B， Zhu Q Y， Siew C K. Extreme learning machine： theory and applications ［J］. Neurocomputing， 2006， 70： 489.

［15］ Jarndal A， Kompa G. A new small-signal modeling approach applied to GaN devices ［J］. IEEE T Microw Theory， 2005， 53： 3440.

［16］ Khusro A， Hashmi M S， Ansari A Q， ?et al . An accurate and simplified small signal parameter extraction method for GaN HEMT ［J］. Int J Circ Theor App， 2019， 47： 941.