關于智能運維中KPI異常檢測與預測的研究

陳云爍?符繁強

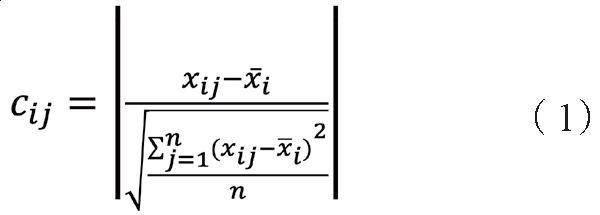
摘要：業務性能指標（key performance indicator，KPI）異常檢測是網絡智能運維中的底層核心技術，對網絡故障發現和修復具有重要意義。針對智能運維中KPI異常檢測和異常預測問題，使用數據特征分析、相關性分析、多元線性回歸分析、機器學習等方法，分別建立KPI異常值檢測差與標準差模型、KPI異常值預測多元線性回歸模型、KPI異常值預測RBF神經網絡模型（RBF—Radial Basis Function），并通過構建評估指標模型對模型預測的優劣進行判斷，給出運營商基站KPI核心指標的異常孤立點、異常周期以及異常值預測。

關鍵詞：異常檢測；異常預測；差與標準差；回歸模型；RBF神經網絡模型

一、問題描述

異常檢測（異常診斷/發現）、異常預測，是智能運維中首當其沖需要解決的問題[1]。這類問題是通過業務、系統、產品直接關聯的KPI業務指標進行分析診斷，本文以運營商基站KPI的性能指標為研究數據，研究三項核心指標。

第一項指標：小區內的平均用戶數，表示某基站覆蓋的小區一定時間內通過手機在線的平均用戶人數；

第二項指標：小區PDCP流量，通過小區PDCP層所發送的下行數據的總吞吐量（比特）與小區PDCP層所接收到的上行數據的總吞吐量（比特）兩項指標求和到，表示某基站覆蓋的小區在一定時間內的上下行流量總和；

第三項指標：平均激活用戶數，表示某基站覆蓋的小區在一定時間內曾經注冊過無線網絡的平均人數。

異常檢測問題：利用提供的研究數據，判斷所有小區的異常孤立點和異常周期以及時間周期的選擇標準。

異常預測問題：根據檢測出的異常值，建立異常值前的數據預測模型，分析預測未來是否發生異常數值。

二、模型假設

1.假設題中給定的數據真實有效；

2.假設提供數據中異常數據只存在少部分；

3.假設運營商基站所覆蓋的區域恒定。

三、符號說明

符號及解釋如表1。

四、異常檢測問題模型的建立與求解

（一）異常檢測問題分析

利用KPI性能指標對小區內的平均用戶數、小區PDCP流量、平均激活用戶三項關鍵指標分析異常檢測問題。

將小區PDCP層所發送的下行數據的總吞吐量（比特）小區PDCP層所接收到的上行數據的總吞吐量（比特）兩個指標進行整合得到小區PDCP流量，提取數據時間、基站編號、小區編號、小區內的平均用戶數、小區PDCP流量、平均激活用戶數進行數據重構。

引入差與標準差的倍數，用來分析異常值，定義：若數據差與標準差的倍數大于2倍以上，則該數據稱為異常數據，判斷三個關鍵指標的異常孤立點和異常周期。

（二） KPI異常值檢測差與標準差模型

1.差與標準差的倍數

以小區內的平均用戶數為例，計算出其對應的差與標準差的倍數，其余指標小區PDCP流量，平均激活用戶按照相同方法操作。

其中，表示第個小區第個數據的差與標準差的倍數，表示第個小區第個數據的值，表示第小區指標平均值，=1，2，3，…，58。=1，2，3，…，。

2.異常值與非異常值判斷

其中，表示異常值的判斷值，表示異常值，表示非異常值。

（三）時間周期分析

由于數據中提供的小區個數多、時間跨度長，本文隨機選取三個小區9天的數值作為展示，分別選取260190015、26019039、26019057小區的三個核心指標數值作數據可視化處理分析其周期性。

通過指標可視化分析圖觀察可知三個小區關鍵指標均存在異常值，針對不同場景的運維雖然會混合多個時間間隔的數據，但具備時序性特點，均為隨時間變化而變化。小區內的平均用戶數小區、平均激活用戶、PDCP流量三項核心指標呈上下起伏的周期變化，為此選取小區內的平均用戶數、小區 PDCP流量、平均激活用戶數時間周期均為1天。

（四）異常孤立點、異常周期的檢測

將已處理的數據用差于標準差的模型計算小區核心指標的相應倍數，求出以26019015、26019039、26019057小區的一段時間中小區內的平均用戶數作為展示和分析。

若一段時間內只有一個異常點則為一個異常孤立點，在一天的時間周期中出現多個異常值則為異常周期。將除以2分別得到，的值。

可求出小區在異常點的總數， =1，2，3，…，58。=1，2，3。以一天為時間周期標準從00：00—23：00時間段中出現多個異常點屬于異常周期，則異常周期的個數，見表2。

五、異常預測問題模型的建立與求解

（一）數據處理

根據58個小區提供的數據對所有指標進行相關性分析[2]，篩選出與小區內的平均用戶數小區、平均激活用戶、PDCP流量三個關鍵性指標相關性較強的指標因子。

三項關鍵性指標相關系數最高的指標數據，例如：平均激活用戶數與最大激活用戶數、空口上報全帶寬 CQI為12的次數、MR 測量上報 RSRP 在 Index4 區間的次數的相關性都比原數據中其他指標數據較高，將三項關鍵性指標的相關系數較高的指標數據提取出來重復異常值步驟，為求解異常預測，做好數據處理。

（二）KPI異常值預測多元線性回歸模型

多元線性回歸分析是通過確定因變量與自變量，分析因變量與自變量之間關系的一種方法，進而確定變量間滿足的方程[3]。本文將問題中所提供的數據進行劃分，前500條數據作為訓練數據，用于訓練變量之間存在的關系，剩余數據用于測試數據訓練的效果，關于小區平均用戶數、平均激活用戶、小區PDCP流量三個關鍵性指標的多元線性回歸分析情況如下：

1.將平均激活用戶數作為因變量，將上文中篩選出與平均激活用戶數相關關系較強的指標作為自變量，使用EXCEL進行多元線性回歸分析。

得到多元線性回歸模型，如下：

1=0+11+22+33 （4）

其中， 0=0，1=0.45， 2=0.21，3=0.16。

2.將小區PDCP流量作為因變量，將上文中篩選出與小區PDCP流量相關關系較強的指標作為自變量，使用EXCEL進行多元線性回歸分析。

可得到多元線性回歸模型，如下：

2=0+1 1+2 2+3 3+4 4+5 5 （5）

其中，0=0，1=0.25，2=0.14，3=0.09，3=0.29，3=0.18。

3.將小區內的平均用戶數作為因變量，將上文中篩選出與小區內的平均用戶數相關關系較強的指標作為自變量，使用EXCEL進行多元線性回歸分析。

可得到多元線性回歸模型，如下：

3=0+11+22+…+1111+1212 （6）

其中，0=0.01，1=0.03，2=-0.08，3=0.01，4=-3.31，5=3.55，6=-0.30，7=-0.004，8=-0.02，9=0.10，10=0.01，11=0.07，12=0.93。

上述方程（4）、方程（5）、方程（6）可以實現對未來時段三個關鍵指標數據的變化趨勢進行預測，以26019039小區的PDCP流量為例，將第500條之后的5個數據指標（UE緩存為空的最后一個TTI所傳的上行PDCP吞吐量、扣除使UE緩存為空的最后一個TTI之后的上行數、平均激活用戶數、最大激活用戶數、MR測量上報RSRP在Index4區間的次數）代入方程（5），計算出預測值，現對指標預測情況與原始數據進行展示，如圖1所示。

（三）預測評估指標模型

為檢驗構建的模型預測效果是否好，現構建預測評估指標模型對建立的KPI異常值預測多元線性回歸模型的優劣進行判斷。

以26019039號小區為例，分別計算小區內的平均用戶數、平均激活用戶數、小區總 PDCP 流量的F1值。

根據建立的多元線性回歸模型，所求出的模型評估值 F1 得出該模型針對小區內的平均用戶數指標預測效果較好，但平均激活用戶數、小區總PDCP流量指標的預測效果明顯欠佳，為此我們考慮再采用RBF神經網絡模型進行求預測。

（四）KPI異常值預測RBF神經網絡模型

RBF神經網絡是將RBF高斯核函數應用于神經網絡的一種模型，RBF神經網絡通常只有三層，第一層是輸入的各個指標原始數值，即輸入層；中間的隱含層是多個高斯核函數，每個高斯核函數都以一個樣本點或者一個聚類中心作為高斯核函數的參數。經過隱含層，數據相當于經過了非線性的變化；之后在第二層和第三層之間采用線性輸出，利用線性加權的方法將隱含層的數據輸出到輸出層，作為最終的預測結果[4-5]。

將三個關鍵性指標作為因變量，對應三個關鍵指標相關性較高指標作為自變量[6-7]，構建RBF神經網絡進行預測，將前200條預測結果與原始數據進行展示。

由于在異常判斷時，數據的差與標準差的倍數得到的值采取了萬分位四舍五入進行計算，為此使用RBF神經網絡模型時會產生較小的偏差，為減小誤差，本文作如下定義。

閥函數：當預測的指標數據與原始數據差的絕對值小于或等于0.05時，表示該預測的結果合理。

閥函數：? ? ? ? ? ? ? ? |- |≤0.05 （7）

其中，為原始數據，為預測數據，，=1，2....，n。

使用F1值對RBF 神經網絡模型的優劣進行判斷，通過使用RBF神經網絡模型得到的F1值都在70%以上，將多元線性回歸模型與RBF神經網絡模型F1值的數據對比，見表3。

從表3可以看出，RBF神經網絡模型的模型評估值F1值遠優于多元線性回歸模型，因此RBF神經網絡模型更適合KPI指標的預測。

六、模型評價

KPI異常檢測與異常預測是智能運維中最核心的問題。本文通過對數據進行特征分析，針對異常檢測問題，提出了KPI異常值檢測差與標準差模型，解決了尋找異常孤立點、異常周期問題；針對異常預測問題提出了KPI異常值預測多元線性回歸模型、KPI異常值預測RBF神經網絡模型，使用評價指標模型判斷出兩個模型的優劣，解決了異常預測問題。但智能運維中的異常檢測無法完全避免故障的發生，只能通過提高系統的穩定性和可靠性，減少故障對系統的影響。因此，在智能運維中，需要不斷地完善技術手段和提高算法的精度，采用多種方法相互協作，才能實現更精確、可靠的異常預測。

參考文獻

[1]陳倩，戴躍偉，劉光杰.面向智能運維的KPI異常檢測模型研究[J].重慶理工大學學報（自然科學），2022，36（06）：181-188.

[2]李軍紅，李付慶，范建民.統計學[M].南京：南京大學出版社，2020.

[3]陳佳佳.面向成分數據的回歸分析研究[M].武漢大學出版社，202008.157.

[4]張澤旭.神經網絡控制與MATLAB仿真[M].哈爾濱：哈爾濱工業大學出版社，2011.

[5]孫永謙，張茹茹，林子涵，等.KPI異常檢測方法評估[J].數據與計算發展前沿，2022，4（03）：46-65.

[6]王速，盧華，汪碩，等.智能運維中KPI異常檢測的研究進展[J].電信科學，2021，37（05）：42-51.

[7]張圣林，林瀟霏，孫永謙，等.基于深度學習的無監督KPI異常檢測[J].數據與計算發展前沿，2020，2（03）：87-100.