基于關聯規則學生成績預警研究

楊令葉?黃學茂

摘要：高校學生成績預警是高校教務管理的重要工作之一，研究高校學生學業預警問題在理論層面和實踐指導層面均具有重要的價值。采用關聯規則算法中的Apriori算法來分析廈門工學院2016級至2018級學生的成績數據，探究每個專業各課程之間的關聯度。在Matlab環境下用Apriori算法對信息與計算科學專業的學生學業成績進行挖掘分析，發現該專業下不同課程間的關聯關系，尤其是對先修課程與后繼課程間的關聯規則的挖掘，及時對掛科的學生預警，并同時給任課教師提供指導，從而提高教育教學管理水平。

關鍵詞：關聯規則；學業預警；Apriori算法

一、Apriori算法介紹

Apriori算法本質是屬于逐層查找迭代算法的一種形式。借助候選項集生成頻繁項集，挖掘出布爾型關聯規則，并計算出相應的支持度、置信度，此兩個標準用來表示關聯規則的強度。其基本思想是利用頻繁項集的先驗知識以遞歸的方法判斷候選集是否為頻繁項集并且找出最大頻繁項集，利用頻繁項集生成僅包含其非空子集的關聯規則。

二、算法的流程及分析

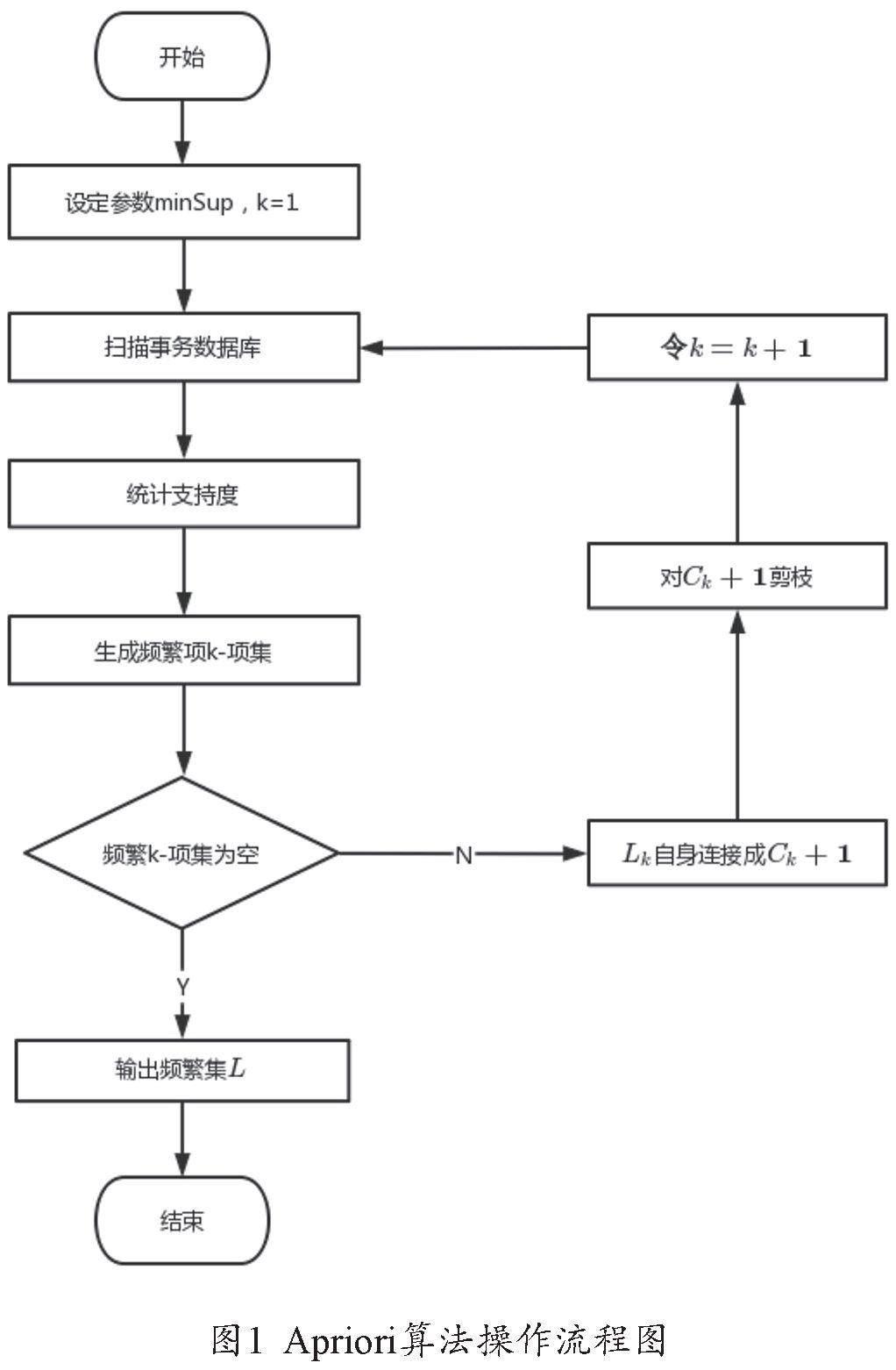
Apriori算法是利用k-項集來生成（k+1）－項集迭代的方法，其操作流程如圖1所示，設定最小支持度minSup、最小置信度minConf。第一步，掃描學業成績數據庫，保留滿足最小支持度的候選項1-項，得到頻繁集1-項集L1；第二步，由L1自身相連生成2-項C2，將得到的C2進行剪枝操作，統計2-項集的項數，刪除不滿足minSup的項集，得到頻繁項集2-項集L2；進行多次迭代，找到滿足條件的最大頻繁項集k-項集Lk，最終得到頻繁項集：L={L1，L2，L3，...，Lk}

Apriori算法挖掘頻繁項集具體的過程如下[1]：

1.連接步驟：Lk-1經過自身連接得到k-項集Ck。如果Lk-1中的某兩個元素（集合）ik-1 和ik-2 的前（k-2）個項是相同，則稱ik-1 和ik-2 是可連接的。所以ik-1 和ik-2 連接產生的結果集是：

i={i1[1]，i1[2]，i1[3]，...，i1[k-1]，i2[k-1]}

2.剪枝：利用任何兩個非頻繁項集的超集都不是頻繁集的性質，如果項集Ck的子集不屬于Lk-1，則該子集是非頻繁，則從Ck中刪除。

3.刪除：利用上文中得到的Ck，統計剪枝后的每一項的項數，刪除不滿足條件的項，最終得到頻繁k-項集Lk。

三、數據準備

所使用的原始數據來源于廈門工學院教務系統內2016級至2018級共計9000余名學生的學業成績數據。為了便于對關聯規則進行挖掘分析，選取信息與計算科學專業學生的學業成績進行挖掘，且在源數據提取時，不考慮補考和重修的成績，只保留學生正考成績。

（一）學生學業成績數據預處理[2]

本次實驗的數據來源于廈門工學院教務管理系統數據庫，具有規范性和真實性。原始數據進行算法分析時需要生成適用于Apriori算法的布爾型數據，進而實現算法在成績數據挖掘中的應用。

1.數據消減

針對缺項數據，則需要刪除這類學生的異常成績數據。

2.數據標準化[3]

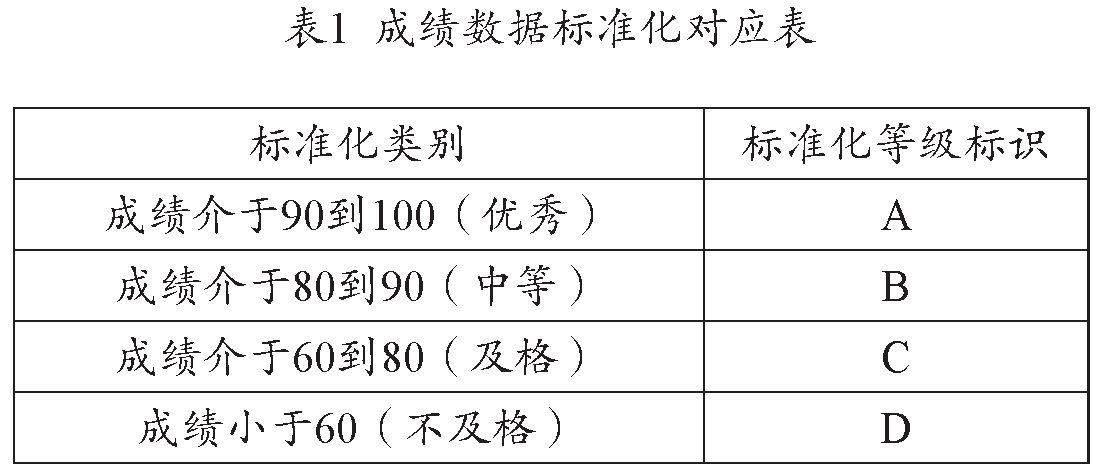
在學生的學業成績表里，少數課程錄入的成績為四級制（優秀、中等、及格、不及格 ）。為了使成績數據在挖掘過程中統一規則，需要針對這類數據進行標準化處理。成績數據標準化對應表如表1所示。對應規則設定完成，再將學生的學業成績數據基于學號作為主鍵進行數據轉化。

3.成績數據離散化

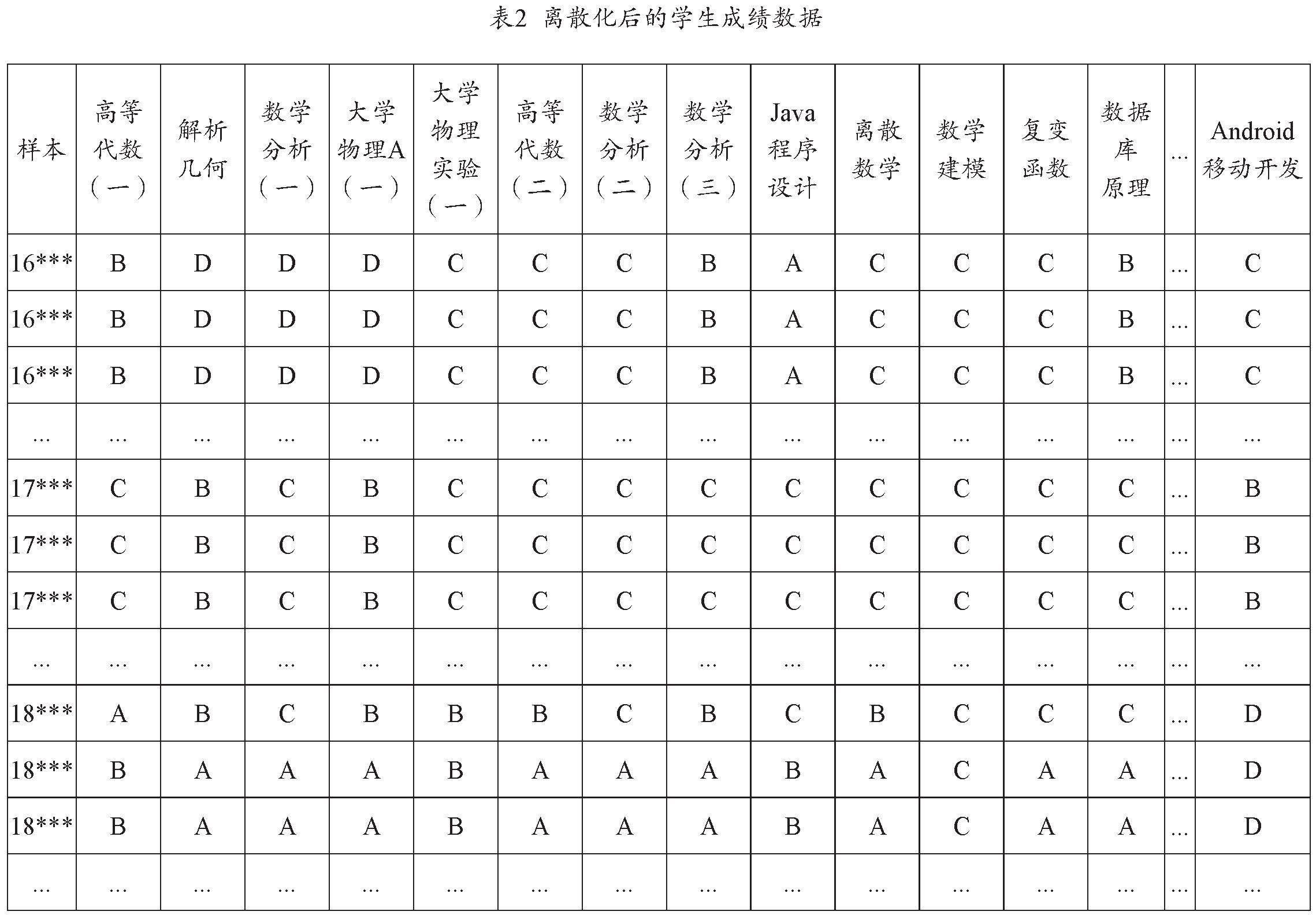
按照Apriori算法函數的作用，將標準化后的學生學業成績進行離散化處理，并且為了簡化表格，把表中列出的全部課程成績按代碼來表示，離散化后的數據表如表2所示。

四、關聯參數閾值確定

首先通過試探法來確定支持度的最佳值，設定置信度閾值minConf=0.9，試探得出當支持度為0.3時，關聯規則分析的結果最具有代表性，因此我們將支持度設置為0.3，并使用Apriori算法來對該數據集進行分析[5]。如表3。

同理通過試探法來確定置信度的最佳值，根據上一步實驗得到的最優支持度minSup=0.3，試探得出當置信度minConf=0.8時，關聯規則分析的結果最具有代表性，由此可得最優置信度設置為0.8，如表4。

由表4可得，最優的關聯規則閾值為：{支持度minSup=0.3，置信度minConf=0.8}。

五、關聯規則結果

在 Matlab2018a 環境下，運用 Apriori 算法對預處理的成績數據進行挖掘，采用上文確定的最優支持度和置信度{minSup=0.3，minConf=0.8}，挖掘出不同的關聯規則。在分析的過程中，我們得到了一個包含了各種課程成績頻繁項集的列表，其中支持度和置信度都達到了預設的閾值。將強關聯規則以列表的形式呈現出來，在本文中，挖掘出的關聯規則，如表5所示。

六、實驗結果分析

本次實驗共挖掘出27個頻繁項集，其中包含了該專業學生的各個成績屬性組合情況。在27個頻繁項集中，選取其中支持度、置信度較高的一些關聯規則進行分析，根據表中列出的關聯規則可知：

（一）規則12，該專業學生在｛高等代數（一）C，高等代數（二）C｝課程中都取得了中等（C）的成績，那么該學生在｛復變函數C｝課程中也很可能取得中等（C）的成績，支持度70.48%、置信度為80.76%，支持度越大，說明在該專業的學生中該三門課程同時取得中等（C）的成績非常普遍，且前置課程的成績對后置課程的成績的影響比較大，影響的概率為80.76%。

（二）規則5：｛數據結構D -> 數據庫原理D｝，該規則的支持度為50.24%、置信度為81.75%，則表明該專業的學生成績系統中顯示有一門｛數據結構｝不及格（D），根據關聯規則得出他需要注意｛數據庫原理｝課程的學習，同時需要加強｛數據結構｝課程的指導及復習。

（三）從規則 10、13、16、27 中可以看到，數學類相關課程的成績與程序語言類，以及專業課的成績存在一定關聯性，其原因是數學類課程是計算機編程邏輯的基礎課程，數學類課程對于學生邏輯思維能力的提升具有不可替代的作用。而語言類編程課程的學習一般都是基于邏輯思維來學習的，所以若是數學類的課程成績較差，后續的語言類課程也會學不好或者出現不及格的現象。

綜上所述，通過本次實驗可以看出，關聯規則挖掘技術可以對學生學業成績之間的關系進行發掘和分析，從而為學生的學習提供有益的指導和幫助，促進學生成長和發展[4]。

參考文獻

[1]王吉.教務數據的分析與預測——以建寧七中為例.北京：清華大學出版社，2018：25-28.

[2]吳蓓.基于決策樹算法的成績預測模型研究及應用[M].北京：人民郵電出版社，2019：13-16.

[3]都娟，翟社平.基于改進 Apriori 算法的高校學生成績預警系統的研究[M]．北京：人民郵電出版社，2018：108-109.

[4]胡金濤.基于C4.5決策樹的學生成績預測教學系統的研究與實現[D].西安：西南交通大學，2017．

[5]毋雪雁，王水花，張煜東.K最近鄰算法理論與應用綜述[J].計算機工程與應用，2017，53（21）：1-7.