連桿蝶閥運動軌跡分析
黎華 蓋曉明 黎勤 田巋

摘 要:連桿蝶閥在很多場合都得到了應用。通過對連桿蝶閥的運動軌跡進行分析,得到了連桿蝶閥各參數之間的關系式和閥板運動軌跡,從而更好的了解閥門的運動特性,對流道進行分析;然后調整各參數,通過求得的關系式進行試算,得到最理想的運動特性。優化設計,以滿足各使用場合的要求。
關鍵詞:連桿蝶閥;四連桿機構;運動軌跡;關系式
THE ANALYSIS OF THE MOTION TRAJECTORY OF THE LINKBUTTERFLY VALVE
Li Hua1,2 Gai Xiaoming1,2 Li Qin3 Tian Kui3
(1.Hebei Province Technology Innovation Center of Metallurgical Equipments? Qinhuangdao 066318, China;
2. Qinhuangdao Qinye Heavy Industry Co., Ltd.? Qinhuangdao? 066318,China;
3.Drilling Technology Research Institute of Bohai Drilling Engineering Co., ltd.? CNPC? Renqiu 062550,China)
Abstract:Link butterfly valve has been applied in many occasions. Through the analysis of the motion trajectory of the link butterfly valve, the relationship between the parameters of the link butterfly valve and the motion trajectory of the valve plate are obtained, so as to better understand the motion characteristics of the valve, analyze the flow channel, and then adjust the parameters. Through the trial calculation of the obtained relationship, the most ideal motion characteristics are obtained, and the design is optimized to meet the requirements of various applications.
Key words:Link Butterfly Valve; Four Bar Linkage; Motion Trajectory; Relation
0 前 言
隨著冶煉技術的不斷發展,冶金閥門的性能也在不斷提高。連桿蝶閥作為一種切斷蝶閥,以結構簡單、體積小、自重輕、動作靈活、密封性能好、使用壽命長、閥門成本相對低等優點[1],在冶金行業被廣泛應用于煉鐵熱風爐系統中,在石化、化工、電力等行業得到應用。
連桿蝶閥屬于蝶閥的一種結構形式, 其閥門的關閉主要依靠內置于流道的一組四連桿機構的動作來實現。因此,相對于其他蝶閥,其流道內的流動非常復雜[2],為了對流道進行分析,需要得到閥門的運動軌跡,通過閥門運動軌跡方程,可以合理選擇設計參數,優化閥門結構。
1 結構特點和工作原理
連桿蝶閥的結構如圖1所示,其主要由閥體、桿系(閥板、主動桿、連板、固定板)、軸端密封組、主軸、驅動裝置等部件組成。
閥門通過驅動裝置所輸出的扭矩使主軸帶動主動桿旋轉90 °完成閥門的啟閉。其中閥板近似平動+翻轉或翻轉+近似平動完成90 °旋轉過程是由四連桿機構控制的。閥門開啟到位時閥板與管道中心線平行;關閉到位時閥板與閥體的密封面平行接觸直至壓緊密封面,達到閥門的密封要求,其傳動機構為四連桿機構,傳動機構如圖2所示(圖2a為閥板關閉位置,圖2b為閥板開啟90 °位置)。
2 連桿蝶閥運動軌跡分析
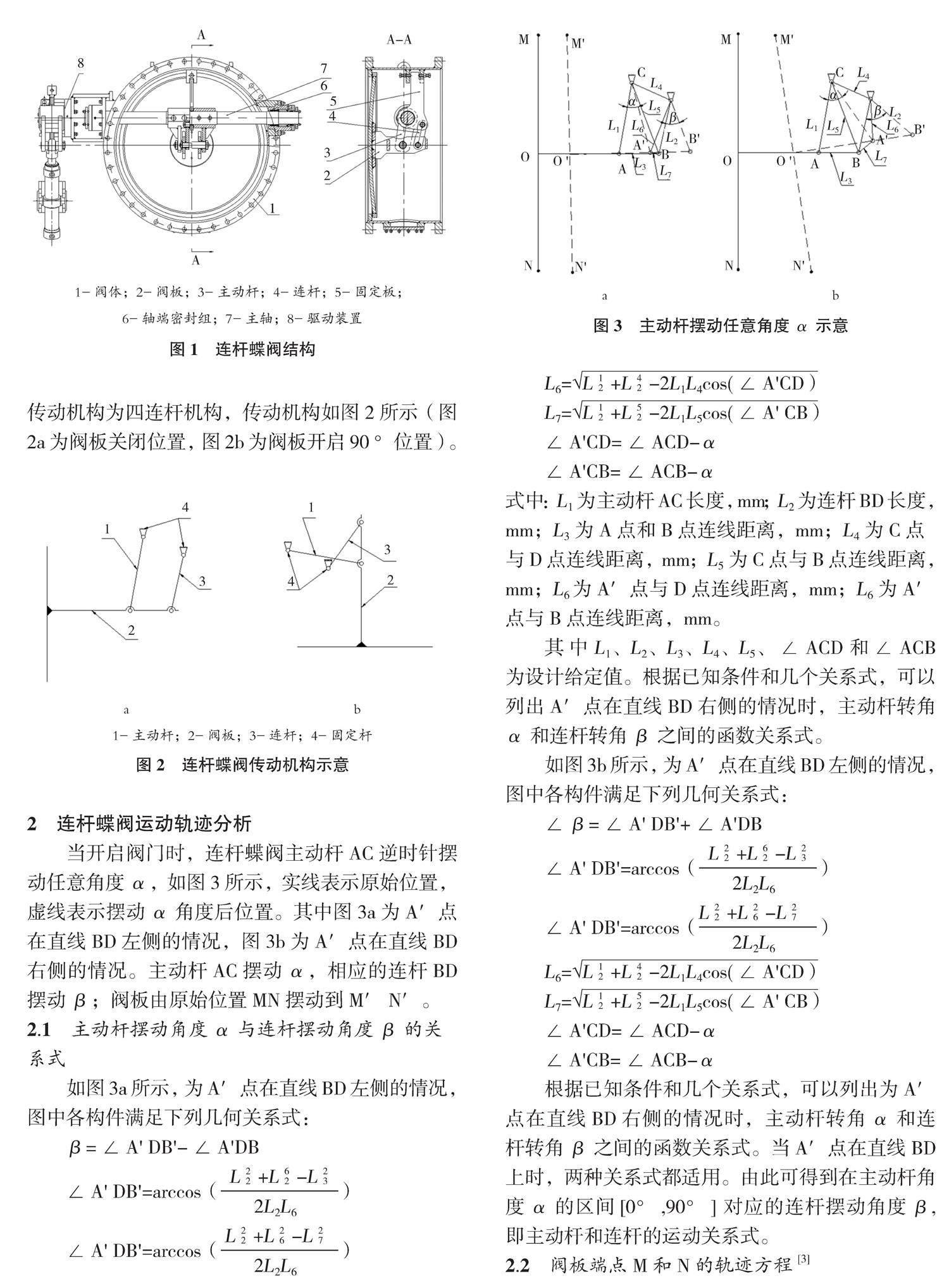
當開啟閥門時,連桿蝶閥主動桿AC逆時針擺動任意角度α,如圖3所示,實線表示原始位置,虛線表示擺動α角度后位置。其中圖3a為A′點在直線BD左側的情況,圖3b為A′點在直線BD右側的情況。主動桿AC擺動α,相應的連桿BD擺動β;閥板由原始位置MN擺動到M′N′。
2.1 主動桿擺動角度α與連桿擺動角度β的關系式
如圖3a所示,為A′點在直線BD左側的情況,圖中各構件滿足下列幾何關系式:
β=∠A' DB'-∠A'DB
L2 2+L6 2-L2 3
∠A' DB'=arccos(——————)
2L2L6
L2 2+L2 6-L2 7
∠A' DB'=arccos(——————)
2L2L6
L6=√L1 2+L4 2-2L1L4cos(∠A'CD)
L7=√L1 2+L5 2-2L1L5cos(∠A' CB)
∠A'CD=∠ACD-α
∠A'CB=∠ACB-α
式中:L1為主動桿AC長度,mm;L2為連桿BD長度,mm;L3為A點和B點連線距離,mm;L4 為C點與D點連線距離,mm;L5 為C點與B點連線距離,mm;L6 為A′點與D點連線距離,mm;L6 為A′點與B點連線距離,mm。
其中L1、L2、L3、L4、L5、∠ACD和∠ACB為設計給定值。根據已知條件和幾個關系式,可以列出A′點在直線BD右側的情況時,主動桿轉角α和連桿轉角β之間的函數關系式。
如圖3b所示,為A′點在直線BD左側的情況,圖中各構件滿足下列幾何關系式:
∠β=∠A' DB'+∠A'DB
L2 2+L6 2-L2 3
∠A' DB'=arccos(——————)
2L2L6
L2 2+L2 6-L2 7
∠A' DB'=arccos(——————)
2L2L6
L6=√L1 2+L4 2-2L1L4cos(∠A'CD)
L7=√L1 2+L5 2-2L1L5cos(∠A' CB)
∠A'CD=∠ACD-α
∠A'CB=∠ACB-α
根據已知條件和幾個關系式,可以列出為A′點在直線BD右側的情況時,主動桿轉角α和連桿轉角β之間的函數關系式。當A′點在直線BD上時,兩種關系式都適用。由此可得到在主動桿角度α的區間[0°,90°] 對應的連桿擺動角度β,即主動桿和連桿的運動關系式。
2.2 閥板端點M和N的軌跡方程[3]
如圖4所示,點M和N為閥板兩個端點,以閥板中心為原點O,建立如圖所示直角坐標系,并作CE垂直AB于E點、DF垂直AB于F點。圖中虛線是當主動桿轉過α角時各構件位置示意,各點在坐標系中的坐標記作A(XA,0),B(XB,0),E(XE,0),F(XF,0),A′(XA′,YA′),B′(XB′,YB′), M′(XM′,YM′), N′(XN′,YN′)。
由圖4中幾何關系可點知A′(XA′,YA′),B′(XB′,YB′)坐標如下:
XA'=XE+L1sin(α-∠ACE)
YA' =L8-L1cos(α-∠ACE)
XB'=XF+L2sin(β-∠BDF)
YB'=L9-L2cos(β-∠BDF)
式中:L8 為C點和E點連線距離,mm;L9為D點與F點連線距離,mm。
根據點A′和B′可列出直線A′B′方程式,如下:
y-YA'? ? ? ? ?x-XA'
———=————
YB'-YA'? ? ? ? ? ?XB' -XA'
即:
YB'-YA'? ? ? ? ?(XA' (YB' -YA' )
y= ————x- —————— +YA'
XB' -XA'? ? ? ? ? ? ?XB' -XA'
由直線A′B′方程式可知,直線A′B′的斜率K=YB'-YA'/XB' -XA' ,設直線A′B′與x軸夾角為γ,則γ=tan-1 (YB' -YA' )/(XB'-XA' )。已知直線M′N′與直線A′B′垂直,則直線M′N′與y軸夾角為λ=90°-|tan-1XA'-XB'/YB' -YA'? |
上述各式中L8、L9、XE、XF、和∠ACE、∠BDF為設計給定值,并且上節已得到α和β的關系式,因此γ也可由α表示出來。
如圖5所示,過M′點作直線a,過N′點作直線b,過點A′作直線A′T,上述各直線均與x軸平行;然后過A′點分別向直線a和直線b作垂線,垂足分別是P、Q,則可得到如下方程兩個參數方程:
XM' =XA' -L10cos(∠M' A' O'-γ)
YM' =YA' +L10sin(∠M' A' O'-γ)? ? ? ? ? ? ?(1)
XN' =XA' -L11cos(∠M' A' O'-γ)
YN' =YA' +L11sin(∠M' A' O'-γ)? ? ? ? ? ? ?(2)
上面方程中,L10 、L11 、∠M' A' O'和∠N' A' O'為設計給定值,且由已知條件知∠M' A' O'和∠N' A' O'相等,并且XA'、YA'、γ均可由α表示,因此XM′, YM′為變量α的函數,方程(1)為點M′(XM′,YM′)中XM′,YM所在曲線的參數方程;XN′,Y N′為變量α的函數,方程(2)為點N′(X N′,YN′)中X N′,YN′所在曲線的參數方程。根據這兩個參數方程,就可畫出閥板端點M和N的運動軌跡曲線。
3 應用實例
為了更直觀的表示各函數之間的關系,這里以DN1400連桿蝶閥為例,繪制各函數曲線。DN1400連桿蝶閥各參數如下:
L1=254、L2=193、L3=140、L4=150
L5=267.4、L8=250、L9=188.4、
L10=L11=708.7、XE=327.5、
XF=464.5、∠ACD=76°、∠ACB=31°、
∠ACE=10.2°、∠BDF=12.56°、
∠M' A' O'=∠N' A' O'=66.5 °
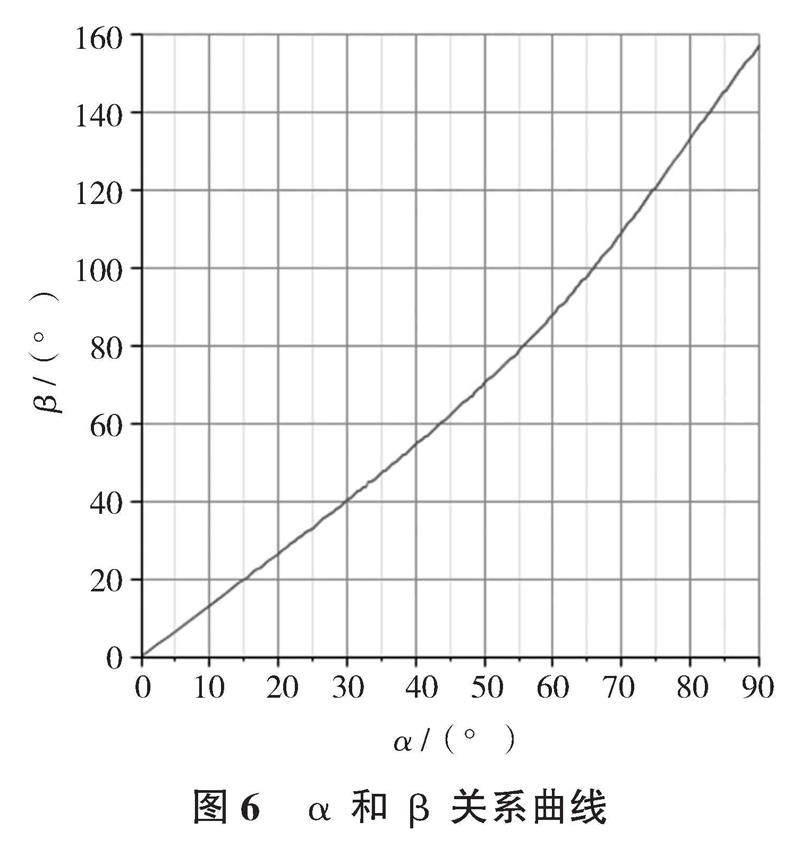
根據求得的各關系式,利用Maple14軟件得到α與β關系曲線。
從圖6可知,β隨著α的增大而增大, 并且β變化速度比α快。
圖7所示為α與閥板所在直線M′N′與y軸夾角λ關系曲線,其中圖7a為閥板從關閉到完全開啟整個過程中α與λ關系曲線,圖7b為α在[0°-20°]變化區間α與λ關系曲線。
從圖7a中可以看出,閥板所在直線M′N′與y軸夾角λ總的變化趨勢為隨α的增大而增大。從圖7b中進一步分析可知,在閥板開啟初期,即α由0°變化到14.5°過程中,閥板所在直線M′N′與y軸夾角λ先增大后減小;在初始位置和主動桿轉過角度α為14.5°時,λ值均為0°。
從圖8、圖9可以看出,當M點橫坐標XM在區間[0,105]變化,對應N點橫坐標XN變化區間[0,200]時,(從參數方程可解出此時對應α變化區間為[0°,35.3°]),閥板近似平動,之后轉動。
4 結束語
連桿蝶閥具有開關速度快,制造成本低,開啟位置準確和占用空間小等特點[4],連桿蝶閥的這些特點使之在很多場合都得到了很好的應用。通過對連桿蝶閥的運動軌跡進行分析,得到了連桿蝶閥各參數之間的關系式和閥板運動軌跡,從而更好的了解閥門的運動特性,對流道進行分析,然后調整各參數,通過求得的關系式進行試算,得到最理想的運動特性,以滿足各使用場合的要求。
參考文獻
[1] 吳懷敏,蘇荊攀,項力勝,等.高溫用金屬密封蝶閥[J].閥門,2018(2):44-45.
[2] 邢衛平,崔兵兵,馬學東.連桿蝶閥的流場分析[J].機械工程師,2011(7):71-72.
[3] 徐付霞.三連桿蝶閥閥板運動軌跡的計算[J].閥門,1994(3):4-8.
[4] 趙文輝.四桿機構蝶閥的設計與應用[J].甘肅農業,2014(2):65-66.

