基于改進蟻群算法的工業機器人路徑規劃研究

朱 敏, 肖 陽, 臧昭宇

(合肥工業大學 電氣與自動化工程學院,安徽 合肥 230009)

路徑規劃是機械臂運動規劃領域的重要研究課題之一,是指在已知的環境下,按照某種方法找出一條從起點到終點的無碰撞路徑[1-4]。考慮到機械臂工作環境的日益復雜,路徑規劃的作用也越來越重要,許多智能優化算法也已經應用于相關領域中,如RRT算法[5]、人工勢場法[6]、A*算法[7]、遺傳算法[8]等。其中,蟻群算法[9]具有正反饋的特點以及并行計算的優勢,已被廣泛應用于解決路徑規劃等問題。為了進一步提高蟻群算法在機械臂路徑規劃中的效果,國內學者對蟻群算法進行了適當優化,文獻[10]在蟻群算法中引入粒子群算法對其部分較優解進行變異和交叉操作,得到了更優的解;文獻[11]采取改進的信息素更新策略和“慣性原則”完成最優操作路徑的搜索;文獻[12]提出建立可視域搜索空間和采用自適應調節揮發系數策略來加快蟻群算法的收斂速度;文獻[13]結合人工勢場法中強化目標路徑的優點,提升蟻群算法的收斂能力,并有效縮短了算法的迭代次數。

本文提出一種改進的蟻群算法,將蟻群劃分為外層蟻群和內層蟻群,分別設計不同的啟發函數來提高搜索效率,并引入安全因子提高機械臂運動的安全性,先利用外層蟻群在無信息素的狀態下規劃出一條參考路徑,增強該路徑上的初始信息素濃度,優化信息素初值,同時改進信息素更新規則并對信息素濃度加以限制,進一步提升內層蟻群的全局尋優能力,搜索得到的最優路徑經由一系列運算和約束得到機械臂的位姿集合,再導入到虛擬機械臂中,由機械臂的運動仿真實驗可知,本文改進蟻群算法能為機械臂在不同環境中規劃出一條符合運動要求的避障最優路徑。

1 機械臂運動學建模

本文以品牌型號為IRB1600的六自由度串聯工業機械臂為研究對象,相應的D-H參數見表1所列,機械臂的各個連桿坐標系如圖1所示。

表1 IRB1600的D-H參數

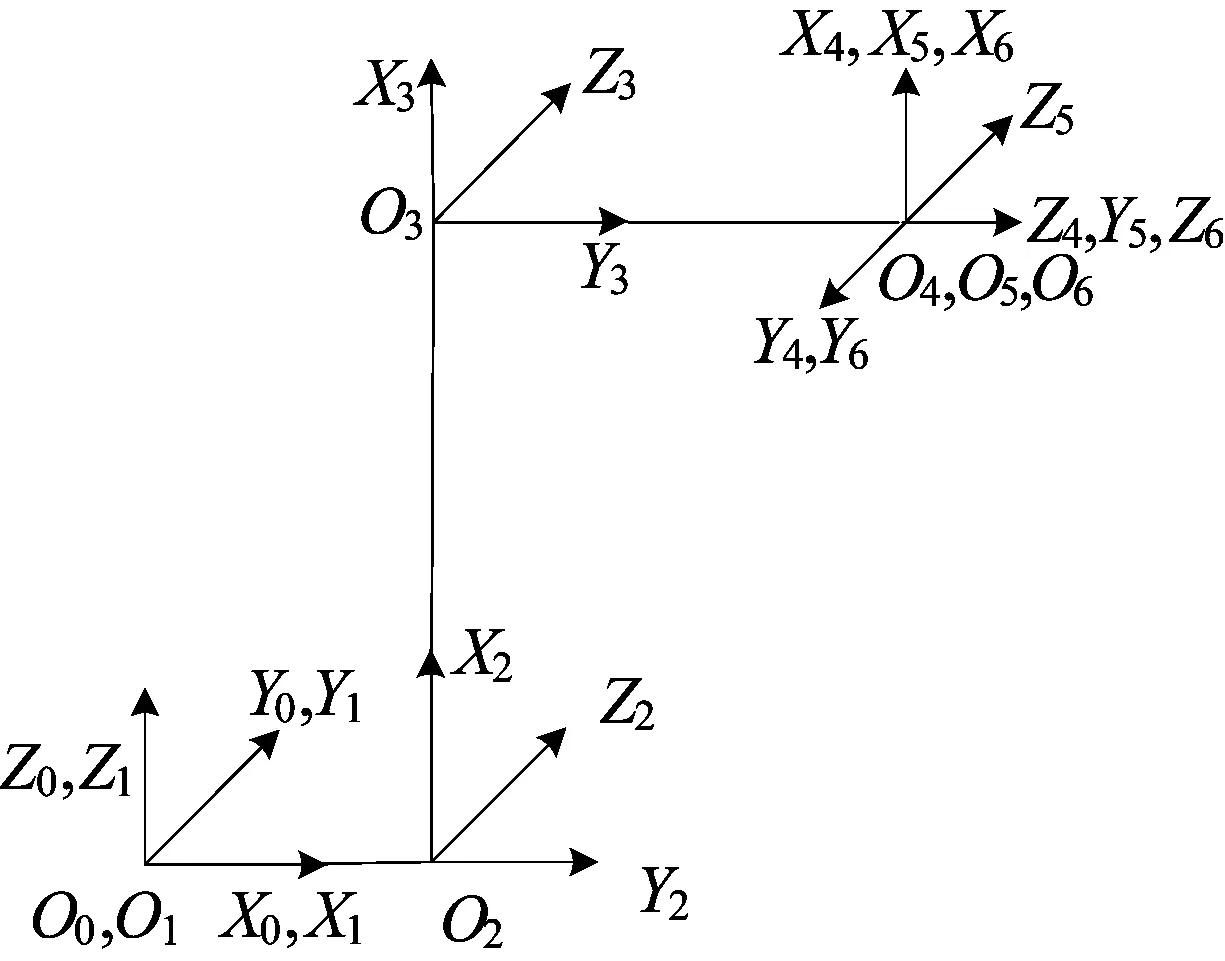
圖1 IRB1600的連桿坐標系

表1中:αi-1為連桿扭轉角,是相鄰軸線在同一平面內的夾角;ai-1為連桿長度,是關節軸i-1與關節軸i之間公垂線的長度;di為連桿偏距,是沿2個相鄰連桿公共軸線方向的距離;θi為關節轉角變量,是兩相鄰連桿繞公共軸線旋轉的夾角。則坐標系{i}相對于坐標系{i-1}的變換矩陣為:

(1)

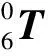
(2)

其中:n、o、a為3個列向量,表示機械臂的姿態;p為機械臂末端的三維坐標。

2 碰撞檢測

在實際工作環境中,障礙物多為不規則物體,建模難度高,本文采用長方體包絡法簡化障礙物,具體做法是將不規則的障礙物用體積最小的長方體包裹起來。

假設機械臂關節i和關節i+1處的坐標分別為Pi(xi,yi,zi) 和Pi+1(xi+1,yi+1,zi+1),則連桿li所處直線的方向為M=(xi+1-xi,yi+1-yi,zi+1-zi)。以長方體平行于x軸的上平面N為例,P1(x1,y1,z1)、P2(x2,y2,z2)、P3(x3,y3,z3)、P4(x4,y4,z4)為上平面N上的4個頂點,通過計算可得到平面N的法向量K=(k1,k2,k3)。若K·M=0,則表示直線與平面N平行;若K·M≠0,則表示直線與平面N相交,必定存在交點P0(x0,y0,z0)。交點若為碰撞點需滿足以下約束條件:首先交點在平面N的內部;其次交點處于連桿線段上。由以上約束可得到如下公式:

(3)

3 基本蟻群算法

蟻群算法在第1次迭代時通過啟發信息尋找起始點到目標點的可行解并分泌信息素,之后的搜索過程又受到信息素的吸引,形成正反饋,逐漸找到全局最優目標并收斂。

3.1 狀態轉移概率

狀態轉移是指蟻群的移動,需要先計算螞蟻的狀態轉移概率再按輪盤賭選擇下一步前往的位置,公式如下:

(4)

其中:集合{allowed}為第k只螞蟻下一步所能選擇的路徑節點集合;α為反映信息素在螞蟻選擇路徑的相對重要程度的參數;β為反映啟發式信息在螞蟻選擇路徑的相對重要程度的參數;τij(t)為連接節點(i,j)之間的信息素濃度;ηij(t)為連接節點(i,j)上的啟發函數,取為1/dij。

3.2 信息素的更新規則

信息素的更新是指量化人工螞蟻在路徑上分泌的信息素及進一步模擬自然界中信息素的揮發過程,公式如下:

(5)

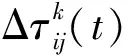
4 改進蟻群算法

基本蟻群算法有以下缺點:每個路徑節點的初始信息素相同且啟發值之間也不存在明顯差異,因此致使蟻群盲目搜索,難以找到全局最優解。為了解決上述問題,本文進行如下改進:

考慮到障礙物的復雜程度和工作空間的大小,將蟻群進行劃分,即

(6)

q=m-p

(7)

其中:p為外層蟻群數量;q為內層蟻群數量;Vobstacle為障礙物所占體積;Vworkspace為工作空間大小;m為螞蟻總數量。

4.1 設置安全因子

根據機械臂能否安全到達,對三維空間內各離散點計算安全值,即

(8)

其中:Safe(Pi)為當前節點Pi搜索域內的安全點;Pi+1為待選節點;S為搜索區域內各離散點的安全因子。若離散點處于障礙物外且機械臂各連桿均未與障礙物發生碰撞,則將該點設為安全點,將其值設為1;否則將其值設為0。

4.2 外層蟻群啟發函數設計

對于外層蟻群來說,需要在無初始信息素的前提下規劃出合理路徑,因此本文在設計外層蟻群啟發函數時需考慮待選節點與目標節點距離的影響,其啟發函數為:

(9)

其中:djg為當前計算的待選節點到目標節點的距離;min(djg)為所有待選節點到目標節點距離的最小值。

4.3 內層蟻群啟發函數設計

鑒于A*算法尋路速度較快,其啟發式成本由采用估價函數f(n)表示,通過f(n)來指導節點的擴展與搜索,每一次都是搜索從起點到終點之間使得f(n)最小的路徑,估價函數方程為:

f(n)=g(n)+h(n)

(10)

其中:g(n)為從起點到當前節點的實際路徑代價;h(n)為從當前節點到終點的預估路徑代價。

因此,將A*算法的估價函數用作內層蟻群的啟發式信息,以便于搜索全局最優路徑,加快收斂速度;同時,將安全因子也添加到內層蟻群算法的啟發函數中,改進后的啟發函數為:

(11)

4.4 信息素不均勻分布

(12)

4.5 信息素更新規則的改進

為提升算法的收斂速度、獲得最優路徑,在更新蟻群信息素時引入狼群的獵物分配機制[14],狼群獵物分配機制的原理是在完成狩獵后,善于狩獵且身體強壯的狼會獲得大量食物,而身體瘦弱的狼只能分得少量食物,這樣整個狼群才能有更高的幾率在下一次狩獵時捕獲獵物,經過多次迭代,該狼群的生存能力逐漸被提高。因此,借鑒狼群的獵物分配機制改進信息素更新規則,最短路徑上的信息素濃度會增加,同時最長路徑上的信息素濃度降低,突出不同路徑信息素的差異化,從而提高了螞蟻中優質種群的生存能力,改進后的信息素更新公式為:

τij(t+1)=(1-ρ)τij(t)+

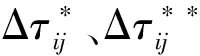
(13)

其中:Lbest、Lworst分別為每次蟻群到達目標節點的最優路徑和最差路徑;δ、ω分別為每次搜索時找到最優路徑和最差路徑的螞蟻數量。

4.6 信息素濃度限制

經過上述改進,蟻群算法的收斂速度得到了提高,但會造成部分路徑上的信息素濃度過高,進而降低算法對其他路徑的選擇,導致搜索出現停滯,為了防止這種情況產生,借鑒最大最小螞蟻系統將信息素的濃度范圍限定在τmin～τmax之間,具體公式為:

(14)

4.7 算法實現流程

(1) 初始化算法參數,設置起點和終點以及安全因子。

(2) 按(6)式和(7)式蟻群分為外層蟻群和內層蟻群,分別設計不同的啟發函數。

(3) 先由外層蟻群在無信息素狀態下進行搜索,將搜尋到的最優參考路徑轉化為初始信息素的強化值,由(12)式空間內各點信息素初始分布。

(4) 再由內層蟻群進行路徑尋優,記錄每次循環的最優路徑。

(5) 按(13)式對信息素進行更新,并按(14)式限定信息素濃度范圍。

(6) 判斷循環次數是否達到最大值,若達到,則對搜索到的最優路徑進行碰撞檢測;否則跳轉到步驟(4)。

(7) 若沒有發生碰撞,則輸出路徑,結束;若發生碰撞,則跳轉到步驟(3)。

算法實現流程如圖2所示。

5 仿真分析

5.1 改進的蟻群算法規劃路徑的平穩性

本文使用MATLAB 2018a軟件,在CPU為corei5-4210U,運行內存為8 GB的Win10計算機上進行實驗。算法中各參數設置如下:α=1,β=5,ρ=0.9,Q=100,m=50,N=100。為驗證使用本文改進的蟻群算法在不同復雜障礙環境下規劃出的路徑平穩性更好,分別使用本文改進蟻群算法、文獻[12]算法以及基本蟻群算法,在如下3種復雜環境下模擬機械臂末端執行器進行路徑規劃。

路徑規劃結果如圖3所示,在3種復雜度不同的環境下,使用本文改進蟻群算法均可以為機械臂規劃出一條符合運動條件限制的避障路徑,根據不同障礙物環境下規劃的路徑來看,使用本文改進的蟻群算法比文獻[12]算法和基本蟻群算法規劃出的路徑拐點更少,而且搜索到的路徑長度也相對優于其他2種算法。因此,使用本文改進的蟻群算法規劃路徑的平穩性要優于文獻[12]算法和基本蟻群算法。

5.2 改進蟻群算法路徑規劃的高效性

為進一步驗證本文對基本蟻群算法改進的高效性,在環境3的條件下,分別用本文改進的蟻群算法、文獻[12]算法和基本蟻群算法模擬機械臂末端的運動規劃路徑,3種算法均進行20次仿真,統計結果見表2所列。3種算法處于最優路徑長度的收斂曲線如圖4所示。

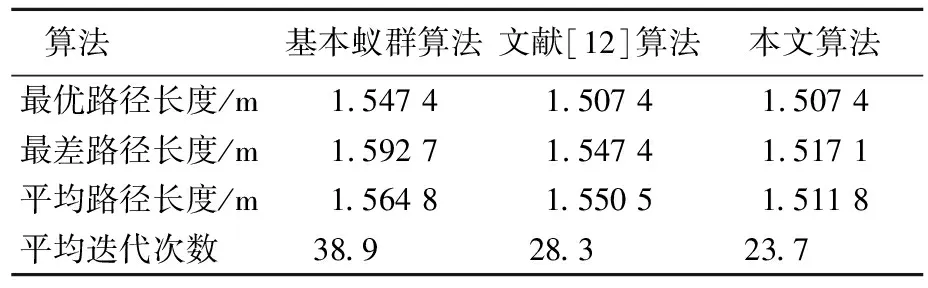
表2 3種算法仿真20次結果統計

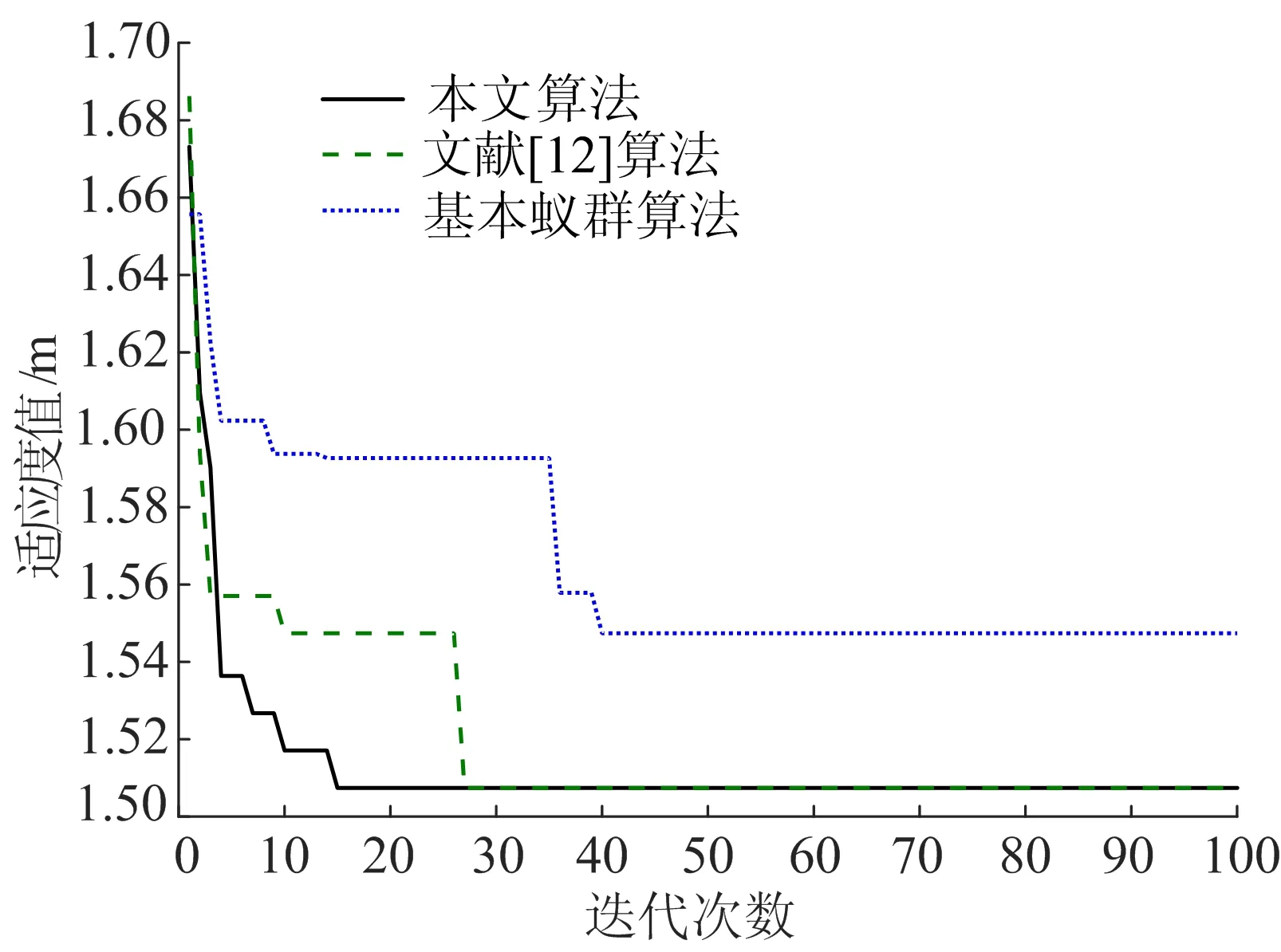
圖4 3種算法最優路徑收斂曲線

依據以上數據可知,使用本文改進蟻群算法模擬機械臂末端進行路徑規劃,比其他2種算法所得的平均路徑代價更優,收斂速度也更快,且在多次仿真中規劃出的路徑穩定性更好,顯著地提高機械臂在路徑規劃中的效率。

為進一步驗證本文改進蟻群算法的可行性,使用RobotStudio軟件中的IRB1600機械臂進行模擬實驗,仿真過程如圖5所示。

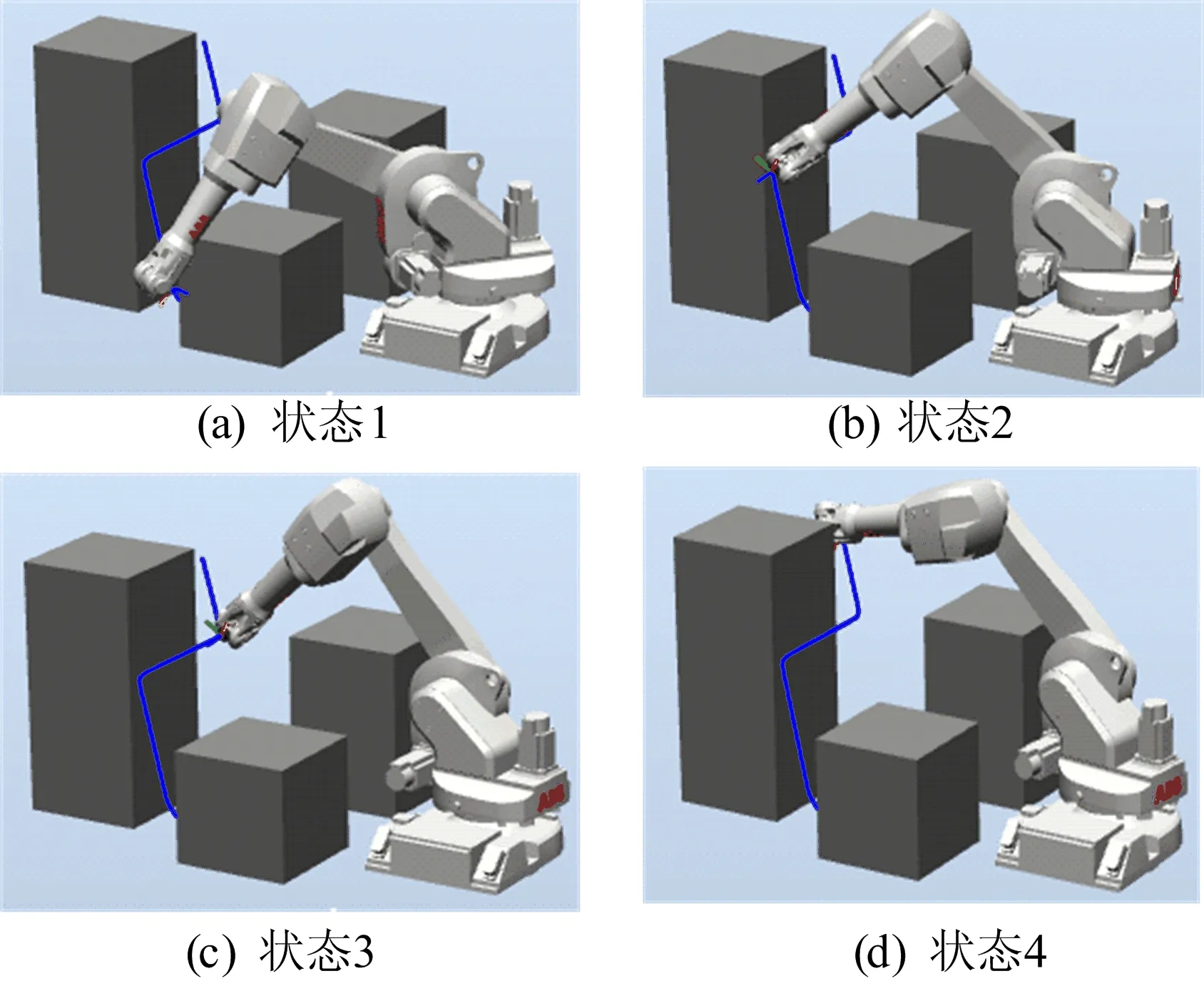
圖5 機械臂避障仿真過程

由圖5可知,機械臂本體未與障礙物發生接觸,體現了本文碰撞檢測算法的有效性。由以上仿真實驗可知,使用本文改進的蟻群算法對機械臂進行路徑規劃時,能夠為機械臂搜索到一條避免碰撞且能滿足運動要求的路徑。

6 結 論

針對蟻群算法在機械臂路徑規劃中存在的問題,如搜索路徑過長、收斂速度慢等,本文對蟻群算法作如下改進:將蟻群分為外層蟻群和內層蟻群,分別設計不同的啟發函數,并引入安全因子提高機械臂運動過程的安全性,利用外層蟻群初始化信息素,引導內層蟻群進行全局尋優,在更新信息素時引入狼群的獵物分配原則,限制部分路徑信息素濃度于合理范圍內。改進的算法通過在MATLAB和RobotStudio中的仿真驗證,結果表明改進后的蟻群算法在收斂速度上,路徑代價相比基本蟻群算法和文獻[12]算法具有明顯的優勢,而且在機械臂仿真中表現良好,可以快速地為機械臂規劃一條最優路徑。