基于ANSYS的某型號后搖臂拓撲優化設計

晏洋，李航，許恢兵，徐生榮，陳朝英，李平

湖北三環鍛造有限公司，湖北襄陽 441700

0 引言

現代汽車對整車的性能要求非常高，包括燃油經濟性、舒適性、操縱穩定性等[1]。相關的研究表明，在滿足整車安全的前提下，賽車的整備質量每降低1 kg，油耗降低0.06%～0.08%，因此對車的零部件進行輕量化設計具有重要的意義[2]。后搖臂作為懸架系統中的關鍵承力件，采用傳統的結構外型設計往往太過笨重，具有較大的安全裕量，無法將材料的性能充分發揮。采用輕量化設計的方法，能夠在滿足設計要求的同時得到更好的優化結構。

拓撲優化作為一個常用的結構優化方法，隨著其技術的快速發展，通過有限元方法進行拓撲優化已經成為輕量化設計的主流。孫瑞晨等[3]采用基于ANSYS的拓撲優化設計模塊對膨脹節萬向環進行輕量化設計，優化后萬向環的質量降低了26.6%，優化后的結構滿足設計要求?？椎路f等[4]采用ANSYS拓撲優化設計模塊對某型號車架結構進行輕量化設計，在滿足整車振動頻率、強度、剛度等約束的前提下，得到的最終車架質量相較于原始車架減輕了3.8 kg，減重幅度達到12.0%，且各項性能指標均有大幅度提升，取得了良好的輕量化效果。逯彥紅等[5]采用拓撲優化方法對某型號渦旋壓縮機機架進行輕量化設計，優化后的機架整體最大應力滿足設計要求，支撐動旋的滑動軸承面最大軸向位移值在允許的范圍內。機架質量由原來的10.4 kg減輕到9.4 kg，減重幅度達到9.8%，達到優化目標結果。Elelwi等[6]利用有限元方法對錐形機翼的變形可變跨度機翼組件進行拓撲優化，固定和移動翼段的結構質量分別減少了16.3 kg和10.3 kg。對優化后的機翼組件使用不同的機械參數進行測試，結果顯示優化后的可變跨度機翼具有最佳的機械行為和機翼結構的完整性以實現多種飛行任務。Chen等[7]基于ANSYS靜力學分析，得到了礦車轉向塊在拉力作用下的總變形和應力。根據邊界條件對轉向塊進行了拓撲優化，并根據拓撲優化的結果對轉向塊進行了優化，最后通過有限元分析進行驗證。結果表明，優化后的轉向塊質量減少了11.7%，結構滿足正常工作的強度和剛度要求。Topa?等[8]通過評估重型商用車后橋連接支架初始設計的強度和變形，確定分析結果中應力分布的關鍵區域，對其進行拓撲優化，改進結構模型，結果表明優化后的連接支架的質量減少了63.0%。Yin等[9]采用有限元分析方法對鏈式提升機的橫梁和杠桿得到了應力變形云圖，然后根據靜力學分析結果進行了拓撲優化，并利用有限元法對結果進行驗證。優化結果顯示優化后的橫梁和杠桿構件比優化前的質量分別減少了20.0%和26.0%。由于優化橫梁和杠桿的應力分別明顯增加了36.0%和47.0%，結果在可接受的范圍內。

目前對于賽車后搖臂的拓撲優化研究還比較少，本文以某型號后搖臂為研究對象，將輕量化設計的理念引入到后搖臂的結構設計中，在保證結構強度及剛度要求的前提下，盡可能地減少構件的整體質量，降低材料成本。對后搖臂模型進行有限元靜力學分析確定后搖臂能夠優化的區域，然后進行拓撲優化設計得到優化模型，再對優化后的模型進行有限元驗證，判斷拓撲優化設計結果是否正確，最終得到輕量化設計目標。

1 后搖臂有限元模型的建立與分析

1.1 有限元模型的建立

采用Solid Works軟件建立某型號后搖臂的三維模型，如圖1所示。

圖1 某型號后搖臂的三維模型

使用ANSYS Workbench平臺中的靜力學分析模塊對某型號后搖臂模型進行有限元分析，采用六面體網格劃分，經多次劃分并驗證網格無關性后，某型號后搖臂的幾何模型轉變為具有物理屬性的有限元模型，共劃分成20 398個單元和104 981個節點，得到的有限元模型如圖2所示。后搖臂的材料屬性見表1。

圖2 某型號后搖臂的有限元模型

1.2 靜力學分析

1.3 靜力學分析結果

經過靜力分析求解計算，得到后搖臂在相應工況下的應力云圖及變形云圖，如圖4和圖5所示。

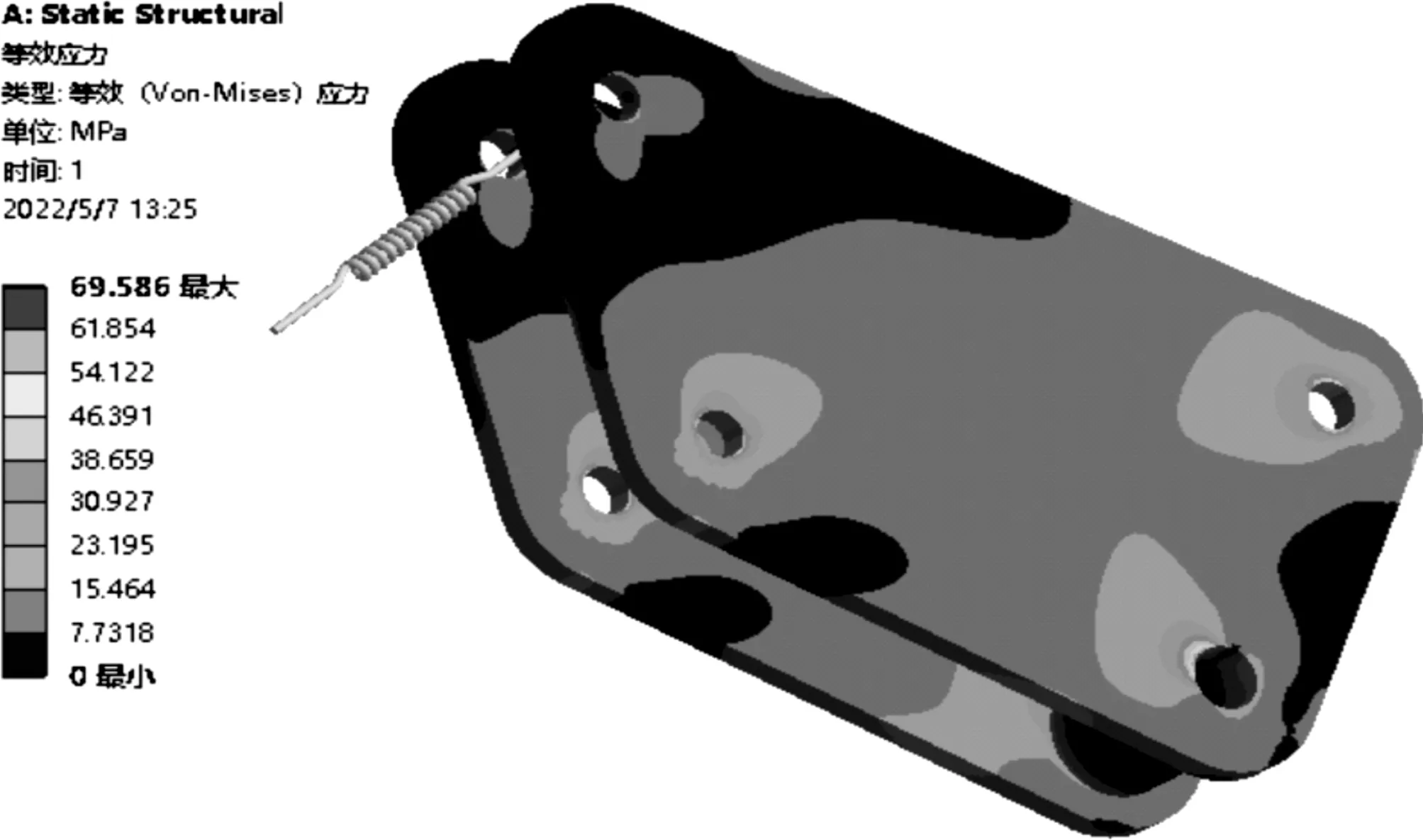
圖4 后搖臂的應力云圖

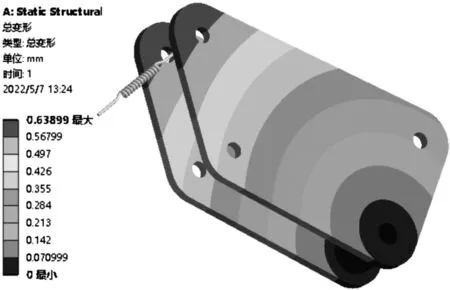
圖5 后搖臂的變形云圖

由圖4可以看出，后搖臂在其樞軸上出現最大應力，最大等效應力值為69.586 MPa，此為應力集中現象，其他部位的等效應力值都比較低，普遍在40 MPa以下。由圖5可以看出，后搖臂最大形變量在與第三彈簧連接孔周圍處，最大形變量為0.638 mm，形變量在合理的變化范圍內。由靜力學分析結果表明，后搖臂的強度和剛度在滿足設計要求的情況下有較大的輕量化優化空間，從后搖臂整體結構的應力和變形分布情況來看，對后搖臂進行整體的結構優化有很大的可行性。

2 后搖臂結構的拓撲優化

2.1 拓撲優化的基本理論

拓撲優化作為結構優化方法具有很好的工程應用前景，拓撲優化方法是根據構件的載荷情況、邊界條件和性能指標，在給定的優化區域內對材料分布進行優化設計的數學方法[8]。拓撲優化方法是由離散體到連續體發展而來的，對于連續體結構的拓撲優化方法有很多，包括變密度法、均勻化法、水平集法等，其中變密度法程序實現簡單、計算效率高，在拓撲優化設計中最常用。變密度法的基本思想是：以連續變量的密度函數形式顯式地表達單元相對密度與材料彈性模量之間的對應關系，這種方法基于各向同性材料，不需要引入微結構和附加的均勻化過程，它以每個單元的相對密度作為設計變量，人為假定相對密度和材料彈性模量之間的某種對應關系，通過有限單元法對連續體結構進行離散化處理，在設計空間內建立一個由有限個梁單元組成的基結構，然后根據算法確定設計空間內單元的去留，保留下來的單元即構成最終的拓撲方案，從而實現拓撲優化[9]。

變密度法優化目標以最大輕量化為目標函數。約束條件包括：滿足優化后體積要小于整個設計域的初始體積，滿足靜力平衡方程，滿足設計變量的范圍為0～1。拓撲優化的數學模型表達式[10]為：

(1)

式中：F為力向量；U為位移向量；K為結構總剛度矩陣；V*為整個設計域的初始體積；V為結構優化后的結構體積；ρ為設計變量；ρe為單元設計變量；ρmin為單元設計變量最小極限值；ρmax為單元設計變量最大極限值；p為懲罰因子；n為結構離散單元總數。

聯合目標函數和預設約束條件得到拉格朗日方程，將約束條件與目標函數結合繼而轉換為零約束問題，采用拉格朗日乘子法構建優化函數[11]：

(2)

式中：λ、λ1、λ2、λ3為拉格朗日乘子，λ為標量，λ1、λ2、λ3為矢量；i為子域內第i個單元；n為單元數目。

由Kuhn-Tucker(K-T)[12]條件建立優化迭代式：

穿好干凈衣物，覺得渾身輕了五百斤，但口渴得厲害，她勉強灌了幾口茶缸水，留個底，把沙棗花插在里面，花苞和葉子蔫頭耷腦的樣子，讓田志芳心疼。內衣簡單在洗澡水里漿過，算洗了。長衣長褲水不夠用就扔在一邊。把鋪蓋擺放好，人軟綿綿地倒在土臺上，眼皮子一閉就睡著了。

(3)

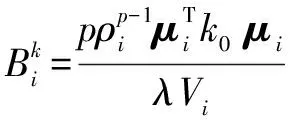
(4)

式中：t為平移限度；η為阻尼系數。

其中平移限度t和阻尼系數η是用來控制迭代穩定及快速收斂。

2.2 拓撲優化分析

為了提高后搖臂整體的靜力學性能，同時可以有效降低自身質量，因此對原有后搖臂進行整體拓撲優化，并依據拓撲優化結果對后搖臂進行結構改進。由于不能夠改變后搖臂的4個安裝孔的位置，故本文選擇后搖臂的優化區域為除去4個安裝孔及外形邊的后搖臂內部區域。

本文使用的拓撲優化軟件是ANSYS Workbench平臺下的拓撲優化設計模塊，拓撲優化設計模塊可以通過給定的載荷情況和邊界條件，在滿足最小柔度即剛度最大化的設計要求情況下實現質量最小化。以拓撲優化計算得到的初步優化模型為參考，由于初步優化模型為不規則的幾何體，需要對初步優化模型進行設計改進，以達到最優化設計結果。然后將最優化設計模型再次進行有限元分析計算，查看計算結果是否滿足設計要求，以此驗證設計可靠性。

將靜力學分析結果導入拓撲優化設計模塊，設置后搖臂的4個安裝孔及外形邊為排除區域，其余部分設置為優化區域，響應約束設置為質量保留百分比為50%，優化算法選擇優化準則法(OC)，收斂容限定義為0.000 1，拓撲優化結果如圖6所示。

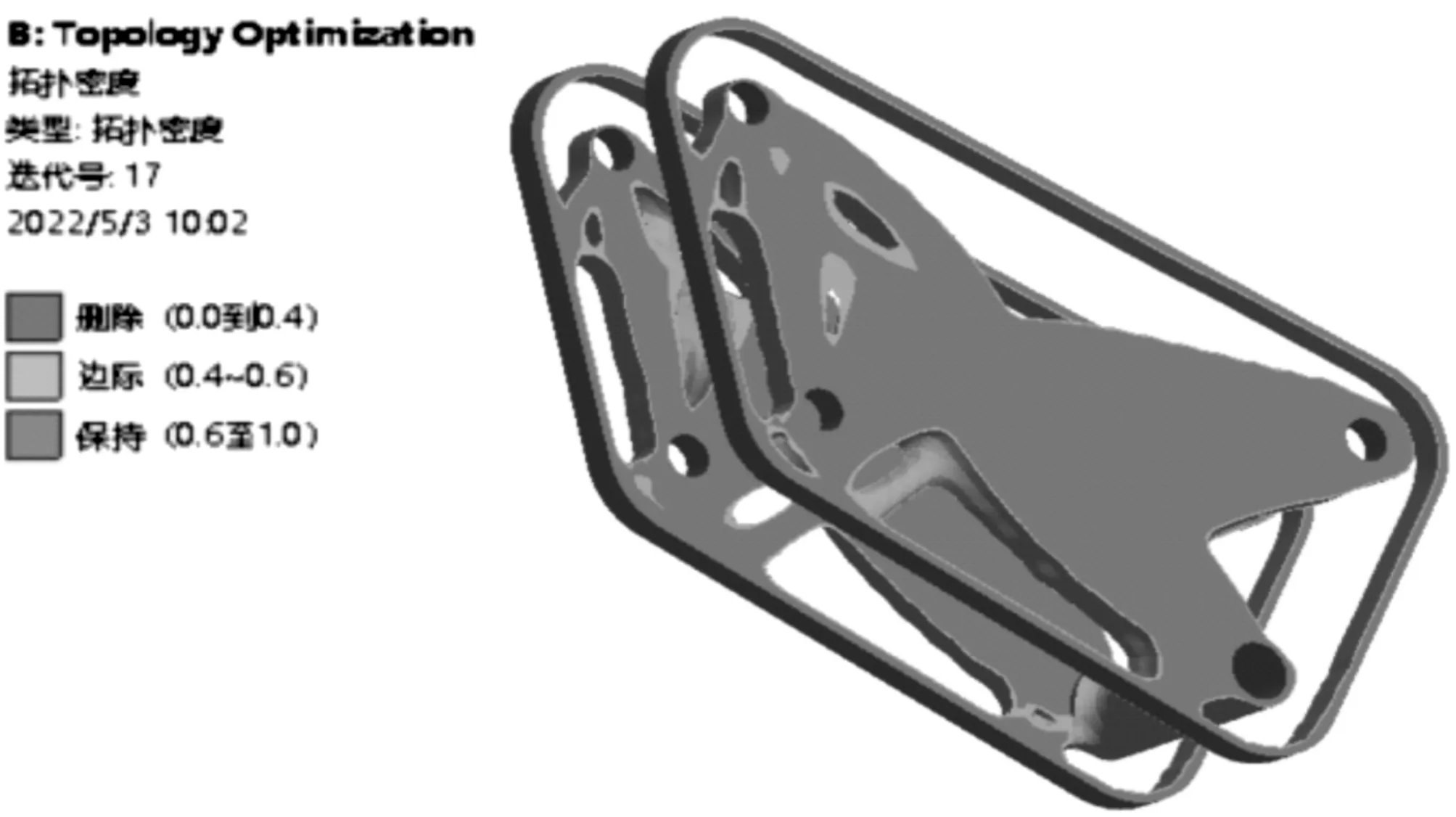
圖6 后搖臂拓撲優化結果

在得到拓撲優化的結果后，以拓撲優化原始模型為參考，對該優化模型進行設計改進，得到的優化設計方案如圖7所示。

2.3 拓撲優化的有限元驗證

將優化后的模型導入到有限元靜力學分析模塊中，計算得到的后搖臂優化后的應力云圖和變形云圖分別如圖8和圖9所示。

圖8 后搖臂優化后的應力云圖

通過對經拓撲優化后改進的后搖臂模型進行有限元分析計算驗證，得到的分析結果表明：優化前后的最大等效應力值均出現在后搖臂樞軸處位置，此為應力集中現象，優化前最大等效應力值為69.586 MPa，優化后最大等效應力值為95.250 MPa，其他部分位置的等效應力值分布情況與優化前大致相似，都在40 MPa以下，整個構件受到的等效應力情況在材料允許的許用應力范圍內。優化前后的最大變形量均出現在后搖臂與第三彈簧連接孔周圍處，優化前最大變形量為0.638 mm，優化后最大變形量為0.637 mm，整個構件的變形量在合理的范圍內。通過對比拓撲優化前后后搖臂的有限元分析結果可知，優化后的后搖臂模型既能夠滿足結構的強度和剛度要求，又能夠滿足設計要求，故拓撲優化的結果是可靠的，對后搖臂的輕量化設計起到了顯著的效果。

本文以有限元分析為基礎的前提下，結合拓撲優化設計方法得到某型號后搖臂的優化模型，后搖臂優化前后設計結果對比見表2。由表可以看出，在滿足設計要求的前提下，某型號后搖臂的拓撲優化設計減材結果為41.075%，拓撲優化減材效果顯著。

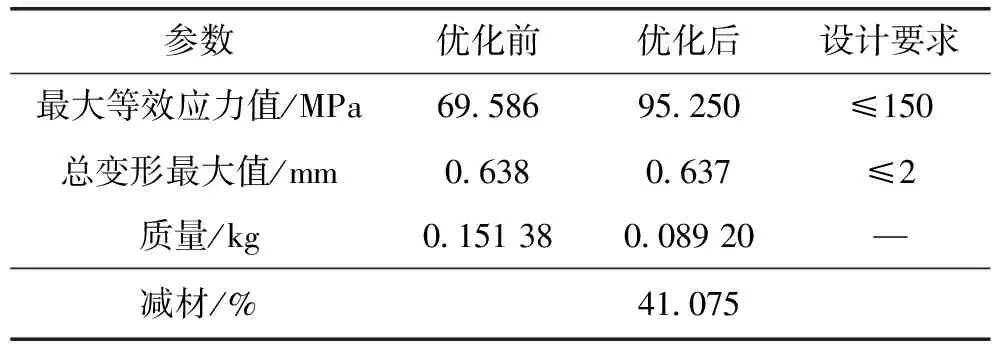
表2 后搖臂優化前后設計結果對比

3 結論

本文通過采用拓撲優化方法對某型號后搖臂進行輕量化設計，針對后搖臂的拓撲優化設計可以得到以下結論：

(1)由靜力學分析發現后搖臂具有一定的輕量化設計空間。后搖臂除在樞軸孔、推桿連接孔及減震器連接孔鄰近范圍內的應力較大外，其余部分應力和變形均較小。

(2)采用ANSYS拓撲優化模塊，以輕量化設計為優化目標，對后搖臂進行拓撲優化，得到優化后的后搖臂模型減重41.075%。對優化后的后搖臂模型進行有限元驗證，結果表明：優化后的后搖臂在強度和剛度性能上能夠滿足設計要求。