彈簧應力松弛載荷的在線測量新方法

蘇懿，王心雨，冉渭，王夢嘉，宋凱強，賀毅

（1.西華大學 材料科學與工程學院，成都 610039；2.西南技術工程研究所，重慶 400039）

應力松弛是材料在一定溫度和固定應變條件下應力隨著時間的延長不斷降低的現象[1-3]，是彈簧失效的主要形式之一[4-5]，具有漸進性和隱蔽性，容易被忽視，通常會造成嚴重的損失[6-7]。應力松弛試驗是研究應力松弛規律，尋找有效預防措施的基礎[8]。因此，改進應力松弛試驗方法對于提高應力松弛試驗數據的可信度，獲得準確的應力松弛規律具有重要的理論及實際意義[9]。

應力松弛試驗方法主要有周期試驗法和連續測量法2 種[10]。周期試驗法作為傳統測試方法，是將彈簧裝夾在特制的夾具中，試驗過程中定期或不定期地將彈簧從夾具中拆卸下來，測量載荷后再裝入試驗夾具中繼續試驗，記錄每次的載荷值，即可繪制彈簧的應力松弛曲線[11]。采用該方法可以同時測試多種彈簧的應力松弛特性，甚至可以進行成批試驗[12-14]，但需要多次裝卸，不僅操作繁瑣，而且所得試驗數據有限，測量誤差較大[15]，如果是高溫試驗，還會引入溫度循環，不利于準確反映真實的彈簧應力松弛規律[16]。連續測量法依然采用特制的夾具，通過應力傳感器測量施加在彈簧上的載荷，雖然可以在不同溫度和應力水平下對彈簧的應力松弛過程進行連續測量[17-19]，但每個傳感器只能測定1 個彈簧，測試效率偏低[20]，且傳感器與彈簧剛性地串聯在一起，遇到振動、碰撞、傳感器損壞等外界干擾后，難以恢復。

為了避免周期試驗法中的繁瑣操作，也為了提高連續測量法的測試效率，結合彈簧的結構特點及加速試驗技術的要求，本文提出了一種在應力松弛過程中測量彈簧載荷的新方法，以圓柱螺旋壓縮彈簧為例，介紹了新方法的2 種實施方式，不僅提高了試驗效率，還有利于獲得更加準確的應力松弛試驗數據。

1 在線測量原理

彈簧應力松弛是指在總形變量不變的條件下部分彈性變形轉變成了塑性變形，進而引起應力降低的現象[21-23]。按照應力松弛的定義，在測量過程中應當保持“總形變量不變”，顯然連續測量法是在“總形變量不變”的條件下完成測量的。周期試驗法則不然，它突破了“總形變量不變”的限制——將彈簧拆卸下來測量，在拆卸、測量和重新裝夾的過程中彈簧的總形變量發生了變化。盡管如此，周期試驗法所得數據依然具有重要的價值，且發揮了重要的作用，這表明在測量過程中依然可以讓“彈簧的總形變量在短時間內發生變化”。據此，在應力松弛試驗過程中，只要將彈簧夾具設計成可動的，測量時使其產生少許位移，完成彈簧載荷–變形量曲線的測試后，可盡快恢復[16]，然后就可以依據載荷–變形量曲線推算出彈簧在裝夾狀態下承受的載荷。這樣既可以避免繁瑣的拆卸與裝夾過程，減少操作誤差，也可以避免測量過程中的溫度循環，提高試驗數據的可信度。

2 測量裝置設計

2.1 單一圓柱螺旋壓縮彈簧的測量裝置

對于圓柱螺旋壓縮彈簧，根據在線測量原理設計了圖1 所示的夾具，讓夾具的上下夾板間距保持恒定，以保障試驗過程中彈簧的形變量恒定。在夾具的上下夾板之間設置可運動的活塞，測量過程中提升活塞，使其離開下夾板，讓施加在彈簧上的力全部轉移到活塞上。在活塞上串聯拉力傳感器和位移傳感器，即可測量到施加在彈簧上的力與活塞的位移，得到彈簧的載荷–位移曲線。測量后讓活塞回到原位，即可讓彈簧回到裝夾狀態，同時使傳感器處于非受力狀態。經過一段時間的應力松弛試驗后，再次提升活塞，并重復上述測量過程，從而實現彈簧載荷的在線測量。

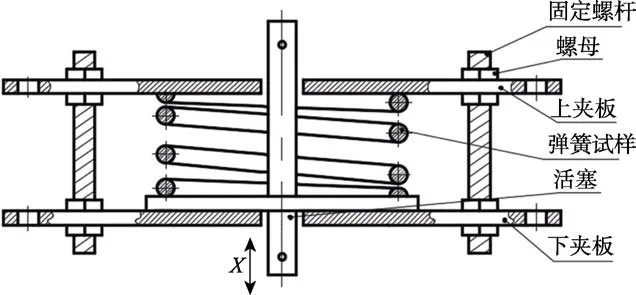
圖1 彈簧裝夾示意圖Fig.1 Schematic diagram of spring clamping

按照應力松弛試驗的要求，需要測量的是彈簧處于裝夾狀態時所承受的載荷，但按照上述的測量原理，測量得到的是彈簧被進一步壓縮后所受的載荷，二者之間有一定的差異。因此需要經過適當的計算，才能得到彈簧處于裝夾狀態時的載荷。

對于螺旋壓縮彈簧，其載荷–變形量特性曲線是直線，按照上述測試原理，可得到如圖2a 所示的載荷–位移（指活塞的位移x）圖。這也是一條直線，經過線性擬合可以得到位移為0 時載荷F0的值，依據F0值，能夠換算出彈簧處于裝夾狀態所承受的載荷。對于數據處理而言，測量過程中活塞的位移x越大，所得到的載荷–位移直線就越長，擬合精度也就越高，這有利于提高測量的準確性。對應力松弛試驗而言，活塞的運動是一種干擾，活塞的位移越小，干擾就越小。可見，提高測量精度和減小測量造成的干擾是相互矛盾的。

圖2 螺旋壓縮彈簧的載荷–位移曲線和驅動力–位移曲線Fig.2 Load-displacement curve (a) and driving force-displacement curve (b) of spiral compression spring

為了緩解這對矛盾，在活塞端部增設了一個圓柱螺旋拉伸彈簧作為緩沖彈簧，將外力施加在緩沖彈簧上，通過緩沖彈簧驅動活塞運動，同時測量緩沖彈簧上端的位移，得到如圖2b 所示的驅動力–位移曲線。緩沖彈簧的設置如圖3 所示。增加緩沖彈簧不僅使活塞運動變得更加平穩[24]，還通過改變測試位移的位置增大了位移量，有利于提高位移測量的準確度。由于緩沖彈簧上端的位移y是活塞位移x與緩沖彈簧的形變量δ之和，所以y既與x線性相關，也與δ線性相關。由圖2b 所示的驅動力–位移曲線可見，驅動力F0；當F>F0時，被測彈簧與緩沖彈簧構成組合彈簧[25]，由于疊加了被測彈簧的位移，驅動力–位移曲線開始變得平緩。由此可見，驅動力–位移曲線由2 段直線構成，F=F0時為轉折點。分別對2 段直線進行擬合，便可求得轉折點的驅動力F0，進而可以計算出待測彈簧處于裝夾狀態所承受的載荷。可見，增設緩沖彈簧后，只需測量緩沖彈簧上端的位移，不再測量活塞的位移，這有利于減小活塞的位移，進而降低測量對應力松弛過程的干擾。此外，增加緩沖彈簧后，活塞與傳感器之間變成了柔性連接，具有一定的減振能力，甚至可以更換傳感器，有利于消除外界擾動，有利于提高測試數據的可信度。

采用周期法進行應力松弛試驗時，可將彈簧裝夾在如圖1 所示的夾具中，定期將彈簧連同夾具從試驗爐中取出來，按圖3 所示的方式測量即可，從而省去了拆裝彈簧的繁瑣操作。

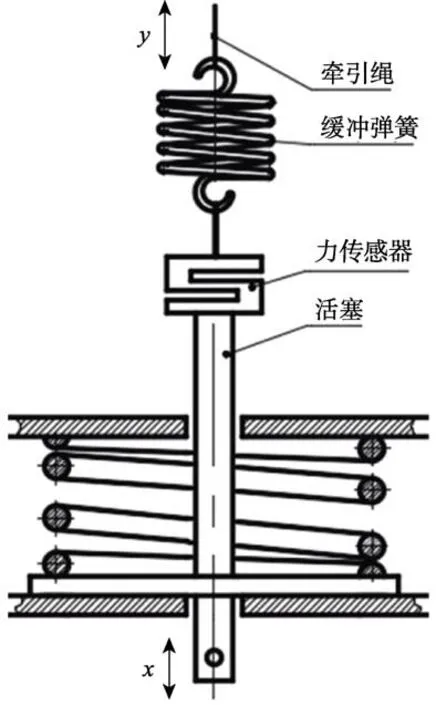
圖3 緩沖彈簧設置Fig.3 Schematic diagram of buffer spring setting

2.2 同時測量2 個因素彈簧的裝置

對于圓柱螺旋壓縮彈簧，如果將2 個待測彈簧串聯起來[25]，并對彈簧的位移進行適當的限制（如圖4a 所示），則在驅動力–位移曲線上可以出現3 個轉折點，如圖4b 所示。其中，第1 個轉折點對應于活塞離開下夾板時的驅動力（記為F1）；第2 個轉折點對應于套筒接觸到上夾板時的驅動力（記為F2）；第3 個轉折點對應于活塞離開墊板時的驅動力（記為F3）。根據這3 個轉折點的驅動力大小，可以計算出彈簧1 和彈簧2 處于裝夾狀態時所承受的載荷P1和P2。

圖4 圓柱螺旋壓縮彈簧的串聯測量方式及驅動力–位移曲線Fig.4 Tandem measurement method (a) and driving force-displacement curve (b) of cylindrical spiral compression spring

式中：k1和k2依次為彈簧1 和彈簧2 的剛度系數；Δ為套筒與上夾板之間的間隙距離；G1為活塞的重量；G2為墊板的重量；G3為限位套筒的重量。可見，在一次測量過程中，可以同時完成2 個彈簧的載荷測量，進而提高測試效率。

由圖3 可見，適當延長夾具中活塞桿的長度，使彈簧和夾具置于試驗爐內，同時將傳感器和緩沖彈簧置于試驗爐外，便可在高溫下測量彈簧的載荷。由此設計搭建了如圖5 所示的在線測試裝置，對于連續測試法樣品，既保證了帶溫連續測量，也可同時完成2個彈簧的載荷測量，提高了測試效率。

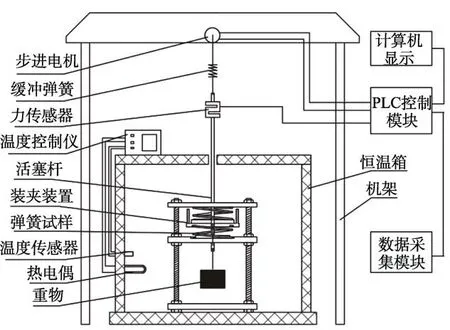
圖5 測試裝置結構Fig.5 Schematic diagram of testing device

3 試驗驗證與討論

為了驗證上述設計方案和測試裝置的可行性，選擇了如圖6 所示的3 種彈簧。其中，鈦合金彈簧用圖3 所示裝置測量，2 種不銹鋼彈簧用圖4 所示裝置測量。試驗中，采用步進電機驅動減速機構提升緩沖彈簧，由于步進電機運行平穩精準，使得提升的距離正比于電機的運行時間，所以沒有設置位移傳感器，僅記錄電機的運行時間便可間接地獲得位移信息。

根據上述測試方法和測試裝置，測得鈦合金彈簧的驅動力–位移曲線如圖7a 所示。圖中的位移是根據步進電機的運行時間換算出來的，圖中曲線出現了明顯的轉折點，且有較好的線性關系。對轉折點兩邊的線段分別進行線性擬合，得到的擬合曲線如圖7b 所示，擬合方程見表1。聯合2 個擬合方程，求解得到轉折點處的驅動力為127.6 N，減去活塞桿的重量28 N 后，得到鈦合金彈簧處于裝夾時的載荷為99.6 N。

圖7 所示的測試結果雖然是一次測量得到的，且僅能計算出測量時刻彈簧承受的載荷，但該次測量中對2 條直線代表的可變載荷進行了數百次測量。表1中兩段直線的相關系數（均大于0.99）和均方差（依次為0.452 4 和0.138 4）表明，測量數據具有較高的可信度。由于測量數據量均大于45，適宜于用正態分布確定測試數據的置信區間。例如對于左側線段，當置信度為 0.95 時，在線段轉折點的載荷區間為(127.6±0.9) N；對于右側線段，當置信度為0.95 時，在線段轉折點的載荷區間為(127.6±0.3) N。由此確定該次測量的結果為(127.6±0.9) N，可見該測量結果具有較高的可信度。

圖7 鈦合金彈簧的驅動力–位移曲線及擬合曲線Fig.7 Driving force-displacement curve (a) and fitting curve (b) of titanium alloy spring

試驗測得不銹鋼彈簧的驅動力–位移曲線如圖8a所示，出現了3 個轉折點，依次對4 條直線段進行線性擬合，得到如圖8b 所示的擬合曲線，擬合方程見表2。聯合相鄰兩端線段的擬合方程，求解得到3 個轉折點對應的驅動力為：F1=26.1 N，F2=35.7 N，F3=74.7 N。與圖7 分析的方法相似，在置信度為0.95時，可以確定3 個測量結果為：F1=(26.1±0.5) N，F2=(35.7±0.4) N，F3=(74.7±0.4) N。根據式（1）和（2），其中，k1=8.9，k2=2.35，活塞重量G1=55.8 N，墊板和限位套筒的重量G2+G3=0.3 N，計算得到裝夾下的載荷P1=46.9 N，P2=16.9 N。

圖8 不銹鋼彈簧的驅動力–位移曲線及擬合曲線Fig.8 Driving force-displacement curve (a) and fitting curve (b) of stainless steel spring

由表1 和表2 可見，所有擬合線的相關系數均高于0.99。在置信度為0.95 時，外推求解得到的轉折點的載荷均在±2%以內，說明該擬合曲線和原始載荷驅動力–位移曲線具有較好的相關性。同時也說明，通過上述測量方法和測量裝置測得的驅動力–位移曲線具有較高的穩定性。更進一步地，這說明根據擬合結果計算得到的彈簧載荷數據具有很高的可信度。

表2 曲線擬合結果Tab.2 Results of curve fitting

按圖1 所示的方式裝夾彈簧，采用周期試驗法先后對80 余件圓柱螺旋壓縮彈簧進行了應力松弛試驗，不僅避免了拆卸彈簧，還確保了試驗數據的可信度。在連續試驗法中，按圖3 所示的方式對應力松弛試驗中的20 余件彈簧進行了載荷測試，獲得了20 多條應力松弛曲線。按照圖4 所示的方式裝夾圖6 所示的2 種不銹鋼彈簧，獲得了18 條應力松弛曲線，所得數據均能滿足試驗要求。

4 結論

綜合上述分析、設計以及試驗驗證，在應力松弛試驗過程中，可以將待測彈簧承受的準不變載荷轉換為緩沖彈簧的連續變化載荷進行測量。在待測彈簧與拉力傳感器之間增加緩沖彈簧，有利于提高系統抗干擾的能力。通過驅動力–位移曲線，推算待測彈簧承受的載荷，有利于提高測量結果的可信度。對于圓柱螺旋壓縮彈簧而言，借助于固定的上下夾板可以使待測彈簧的壓縮量保持恒定，借助于活動的活塞可以使待測彈簧進一步被少量壓縮。進一步改進夾具后，還可以將2 個待測彈簧安裝在同一夾具試驗，從而提高試驗與測量效率。