預制構件生產-運輸-裝配一體化的建造調度優化

秦旋, 朱倩影, 韓家玄

(華僑大學 土木工程學院, 福建 廈門 361021)

傳統建筑業在施工過程中會產生大量建筑垃圾、噪音和揚塵等污染物,這與我國低碳環保的發展理念相悖,亟待向綠色建筑方向轉變[1].在此背景下,裝配式建筑得到大力推廣和發展.目前,預制構件的生產、運輸與裝配3個階段的管理在很大程度上仍依賴于過往經驗,缺乏聯動機制[2],存在調度不合理、運作效率低、成本居高不下等問題[3].因此,從預制構件生產-運輸-裝配一體化建造出發,優化預制構件全階段調度,對推動我國裝配式建筑發展具有重要意義.

我國裝配式建筑起步較晚,只有少數學者將預制構件生產、運輸與裝配3個階段作為一個整體過程進行全階段優化研究.Anvari等[4]首次將預制構件全階段的優化問題作為擴展型柔性作業車間調度(REFJSS)問題,并采用多目標遺傳算法解決REFJSS問題,從而最小化最大完工時間和項目總成本,以及最大化安全性.Khalili等[5]在整個建設周期范圍內解決預制構件的調度問題,將預制構件的生產、運輸與裝配3個階段作為一個完整過程,建立預制構件模塊單元調度模型,并采用混合整數線性規劃(MILP)求解該模型.

目前,對于預制構件調度優化問題,大部分學者根據流水車間調度理論進行建模[6-8],并采用啟發式算法求解該模型.基于此,本文研究預制構件生產-運輸-裝配一體化的建造調度優化.

1 全階段調度優化模型

1.1 預制構件全階段工作流程

裝配式建筑預制構件的生產階段與運輸階段都屬于預制構件的供應鏈范疇,將生產與運輸階段合并成一個擴展的生產過程.預制構件生產-運輸-裝配9 道工序流程,如圖1所示.

圖1 預制構件生產-運輸-裝配9 道工序流程

1.2 混合流水車間調度問題

混合流水車間調度問題(HFSP)在流水車間調度問題(FSP)的基礎上進行擴展[9],FSP工件的每道工序僅對應著一臺固定的加工機器,而HFSP工件的所有或部分工序對應著多臺并行機器[10].由于HFSP工件某道工序對應的若干臺并行機器的屬性是完全相同的,因此,每個并行機器加工該道工序所耗費的時間也是一樣的.

HFSP需要滿足以下4個假設條件:

1) 所有工件的各道工序都可以在對應的任意一臺并行機器上加工;

2) 同一加工階段對應的所有并行機器都是相同的;

3) 某一時刻,一道工序只能在一臺并行機器上加工且不能中斷;

4) 某一時刻,一臺并行機器只能加工一道工序.

混合流水車間調度問題的加工流程,如圖2所示.圖2中:εk表示第k個工序所對應的并行機器的數量.E={ε1,ε2,…,εk}表示混合流水車間調度問題中各工序上并行機器的數量組合.顯然,當εk=1時,HFSP即轉化為FSP.與 FSP類似,HFSP的優化目標通常為最小化最大完工時間.

圖2 混合流水車間調度問題的加工流程

1.3 預制構件全階段調度優化模型

Chan等[11]認為預制構件的生產階段調度問題本質上是屬于FSP.將預制構件的生產-運輸-裝配全階段等效成一個擴展型的生產階段,因此,預制構件的全階段調度問題也可以等效成HFSP.

1.3.1 基本模型 1) 參數設置.預制構件全階段調度的9道工序對應HFSP工件的工序(Nk,k=1,2,…,9);預制構件全階段調度的單個或單批預制構件對應HFSP工件,把單個或單批預制構件稱為一個作業(Ji,i=1,2,…,n);與HFSP類似,預制構件全階段調度的每道工序也對應多臺并行機器(機械設備與人工資源的組合),設jk,m為工序Nk的各并行機器的編號,k=1,2,…,9;tP,Ji,Nk為作業Ji在工序Nk上的加工處理時間;tP,Ji,Nk,jk為作業Ji在工序Nk上的第jk,m個機器上的加工處理時間,對于?jk,m,tjk,m≡tP,Ji,Nk,jk,m;tC,Ji,Nk為作業Ji在工序Nk上的完工時間;tC,max為所有作業中的最大完工時間.

2) 基本約束條件.引入0-1決策變量XJi,Nk,jk,m,有

(1)

由于一臺并行機器在某一時刻只能加工一道工序,因此有

(2)

同樣地,一道工序某一時刻只能在一臺并行機器上加工,因此有

(3)

各個加工階段的機器按照相同的加工順序加工所有FSP工件,而HFSP工件每道工序都存在若干并行機器,各道工序上不同工件的加工順序是不相同的,因此,不考慮各個作業之間的順序約束,僅考慮同一作業內工序之間的順序約束,即某工序開始時間不得早于其前面工序的結束時間,有

tC,Ji,Nk≥tC,Ji,Nk-1+tP,Ji,Nk.

(4)

在工序N9(安裝工序)上,不同的作業滿足一定的安裝順序,某一作業的安裝開始時間不得早于其前面作業的安裝結束時間,由此可得到工序N9上作業執行順序的約束條件為

tC,Ji,N9≥tC,Ji-1,Nk+tP,Ji-1,Nk.

(5)

最后,由于各個工序階段對應的并行機器數量并不是充足的(通常會遠低于作業的數量),因此,假設第k個工序Nk對應的并行機器的數量上限.特別地,在工序N4(養護工序)上,通常所有作業是可以并行加工的,因此,需考慮養護工序階段具有足夠多的機器.

3) 目標函數.設函數f1(E)表示作業的最優調度排序方案對應的最短完工時間,即

f1(E)=min(max(tC,Ji,N9)).

(6)

設函數f2(E)表示在給定某一種并行機器數量組合E時,全部并行機器所產生的總成本為

f2(E)=UET

.

(7)

式(7)中:U=(μ1,μ2,…,μ9)T.

特別地,工序N4的機器幾乎不產生成本,因此,令μ4=0,函數f2(E)可進一步表示為

(8)

全階段調度模型的最終目標是實現雙目標優化,即求解出一種機器數量組合E和一種調度排序方案使得函數f1(E)和函數f2(E)同時達到最小化.雙目標優化問題取值為min(f1(x),f2(x)),x∈Ω,x表示問題的可行解,Ω表示可行解的集合.

1.3.2 雙目標優化與熵權法 由于函數f1(x)和函數f2(x)分別表示時間和成本,量綱不統一,需要將兩個函數的值進行統一量綱處理.采用min-max線性歸一化方法將兩個函數的原始值映射到[0,1]區間內,由于函數f1(x)和函數f2(x)均為成本型函數(函數值越小雙目標優化問題越優),相應的歸一化函數為

(9)

式(9)中:歸一化后的函數F1(x)和F2(x)相當于函數f1(x)和函數f2(x)的評價指標,函數F1(x)和函數F2(x)值越大,雙目標優化問題越優.

優化模型采用線性加權和法將雙目標優化問題轉化成單目標優化問題.轉化后的單目標優化問題的數學表達式為

maxF(x)=w1F1(x)+w2F2(x),x∈Ω.

(10)

式(10)中:歸一化后的函數F(x)為所有可行解的評價函數(最終的目的是找到函數F(x)最大的解);w1和w2分別為函數F1(x)和函數F2(x)對應的權重,也分別為函數f1(x)和函數f2(x)的權重,w1,w2>0,w1+w2=1,且權重通過熵權法確定[11-12].

2 改進的雙種群遺傳算法

遺傳算法是一種典型的元啟發式算法,通過優勝劣汰的方式選擇優化問題的最優解或近似最優解[12-13],是一種高效、并行、隨機的全局搜索尋優方法.在求解較為復雜的組合優化問題時,相對一些常規的優化算法,遺傳算法能夠快速獲得較好的優化結果[14-15].

FSP作為典型的非確定性多項式(NP-hard)問題,應用遺傳算法求解具有非常好的效果[16-18].預制構件全階段調度模型是基于HFSP進行建模的,因此,遺傳算法也適用于最優調度排序方案的求解.為了提升求解的準確性與效率,對遺傳算法做一些改進.改進的遺傳算法流程圖,如圖3 所示.圖3中:n為迭代次數.

圖3 改進的遺傳算法流程圖

由圖3可知:在改進的遺傳算法流程的循環體中,交叉操作放在適應度計算步驟之前,也就是每代種群在計算適應度之前都要經歷一次交叉操作,而這個交叉操作會產生一個和原種群同樣規模的新種群(或稱子代種群);新種群與舊種群合并,形成一個雙種群,對雙種群的全部個體適應度進行計算、選擇和變異等;雙種群的進化方式能顯著提高遺傳算法的搜索效率(這是改進后的遺傳算法的最大特點),除了設置雙種群,也改進了算法的編碼方式和交叉方式.

3 仿真案例分析

3.1 案例背景

將某裝配式建筑的某兩個標準層(2F,3F)涉及的預制構件類型和尺寸劃分成 12 個作業,為了貼合實際工程情況,各個作業在安裝階段都要滿足一定的安裝順序(如 2F 構件要先于 3F 構件安裝).所有構件的養護都采用蒸汽養護方式,并且假設養護窯的數量足夠多,能夠滿足當前所有構件同時進行養護.構件運輸采用相同的專業車輛,每輛車一次只能運送一個作業的構件,構件采用塔吊結合安裝班組(假設安裝班組只有一個)進行安裝.作業的其他各道工序有若干個相同且獨立的機器設備或人工班組,或二者的組合.各作業在 9 道工序上的預計加工處理時間,如表1所示.

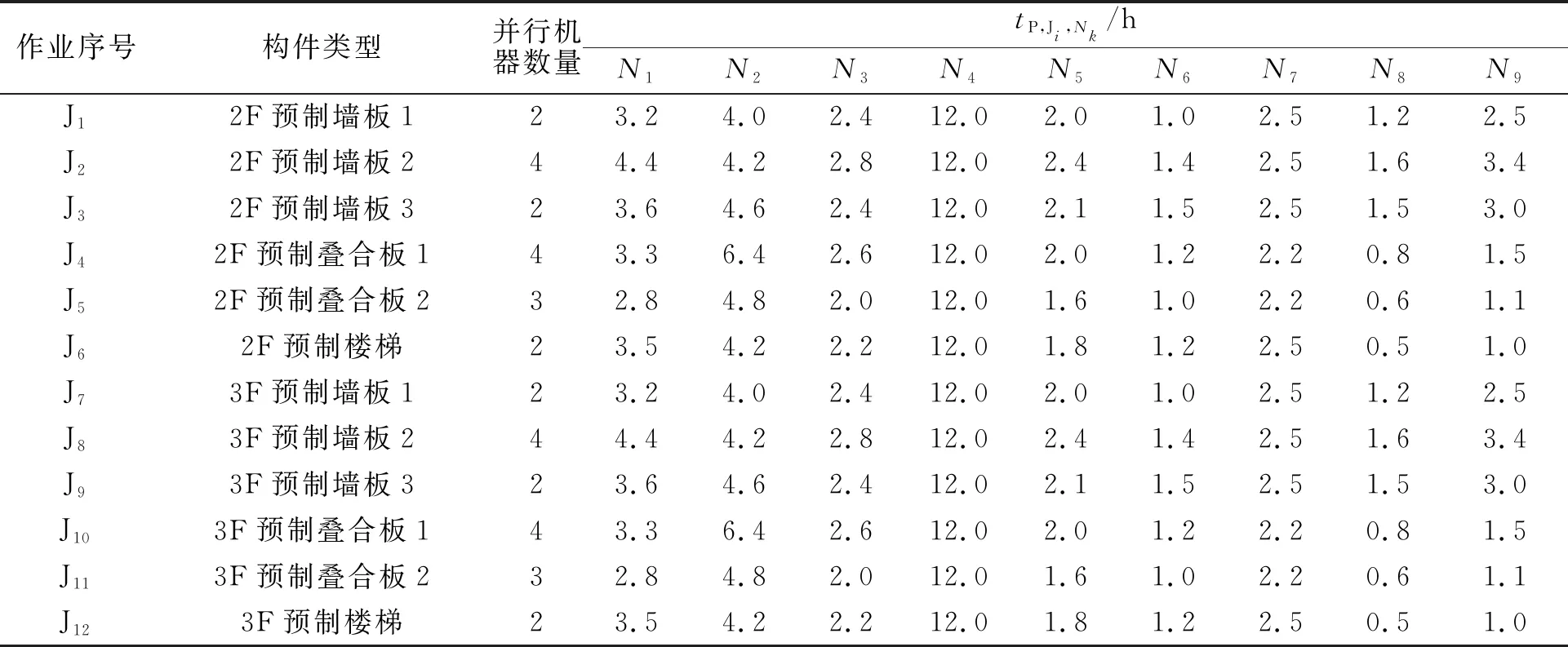
表1 各作業在 9 道工序上的預計加工處理時間

規定工序N9的并行機器的數量上限為1,工序N7(運輸工序)的并行機器數量上限為6,工序N4并行機器數量為L(L是一個足夠大的數,且恒有L>12),其他工序的并行機器數量上限為3,則并行機器的數量上限組合E=[3,3,3,L,3,3,6,3,1].假設N1至N9各道工序上每臺機器的成本已知,令U=[5.0,7.0,10.0,0,5.0,6.0,0.5,5.0,15.0]為各道工序上總機器成本組合,其中,成本為無量綱.

3.2 全階段調度優化問題的求解

3.2.1 最優調度排序方案的求解 采用 MATLAB軟件進行編程,采用改進的雙種群遺傳算法求解仿真案例的最優作業調度排序方案.除了已知的加工時間矩陣和機器數量組合E之外,其他參數的設置如下:最大迭代次數為100;種群規模為80;變異概率為0.95;情況1～情況3的并行機器數量組合分別為E1=[1,1,1,L,1,1,1,1,1],E2=[2,2,2,L,2,2,2,2,1],E3=[3,3,3,L,3,3,6,3,1].令L=50,得到各代最優個體適應度曲線和最優作業調度排序方案甘特圖,分別如圖4,5所示.圖4,5中:tC,min為適應度(最短完工時間).

(a) 情景1 (b) 情景2 (c) 情景3

由圖4可知:情景1在第1次迭代時就已經得到最小適應度(81.2 h),此后的迭代都收斂于相應的最優值;情景2在第20次迭代時得到最小適應度(55.4 h),此后的循環迭代中每代種群中的最優值都為該值;情景3在第3次迭代時就收斂到了最小適應度(53.8 h),此后的迭代最優值都為該值.

由圖5可知:情景1的各道工序(除工序N4外)的并行機器數量都設為1,在這種特殊的機器數量組合下,各作業的調度順序呈現很強的規律性,同時,這種情況下最優完工時間在所有不同組合情況中是最長的,該調度方案也可作為其他情況的對照方案;相比于情景1,情景2的并行機器數量擴大了一倍,相應的最短完工時間也大大縮短了25.8 h,且最優調度方案是不固定的,可存在多個最優解,沒有明顯的規律性,在工序N9上的作業加工順序都嚴格滿足相應約束條件;相比于情景2,情景3的并行機器的數量雖然增加了不少,但最短完工時間縮短了1.4 h,這說明當并行機器的數量足夠多時,繼續增加并行機器帶來的時間收益會越來越小;在規定的機器數量上限以內,存在一個或多個機器數量組合的臨界點,同時,也存在某種機器數量組合能使最短完工時間和總機器成本都最小化.

(a) 情景1 (b) 情景2 (c) 情景3

3.2.2 雙目標優化問題的求解 雙目標優化問題的目的是尋找一種或多種并行機器的數量組合,最大化獲取“時間+成本”的綜合收益,即最小化最短完工時間和總機器成本.首先,需要確定并行機器數量組合的種類數量,為了精簡求解范圍,假設工序N7,N8,N9的并行機器數量是固定的,分別為6,3,1,令工序N4的并行機器數量L=50.因此,并行機器數量組合的種類與剩下5道工序的機器數量取值有關,并且該5道工序的機器數量上限皆為3,則并行機器數量組合共有 35=243 種(按 1 至 243 的順序對并行機器的所有數量組合進行編號).

根據已知的總機器成本組合U=[5.0,7.0,10.0,0,5.0,6.0,0.5,5.0,15.0]及并行機器數量組合E=[a,b,c,50,d,e,6,3,1](a,b,c,d,e=1,2,3),采用MATLAB軟件進行編程,求解每種機器數量組合下的函數f1(x)和函數f2(x),最終得到243對值.最短完工時間函數和總機器成本函數的散點圖,如圖6所示.

圖6 最短完工時間函數和總機器成本函數的散點圖

由圖6可知:離散點在縱軸上分層明顯,表明在某一固定總成本下,不同的機器數量組合帶來的時間收益可能會大相徑庭;幾乎每一個函數f1(x)的值都對應著許多個函數f2(x)的值,并且函數f2(x)的值跨度較大,這表明在時間目標固定時,可以通過改變并行機器數量組合降低成本;越靠近左下角的離散點越優.

利用min-max公式,對所求的243對值進行歸一化處理,得到相應的評價因子指標函數F(x)值(F1(x)值,F2(x)值).根據F(x)值,利用熵權法,采用MATLAB軟件進行編程,求解得到的F1(x)指標權重為w1=0.832,F2(x)指標權重為w2=0.168,指標權重w1,w2也是雙目標優化中目標函數f1(x)和f2(x)的權重.

最短完工時間函數,總機器成本函數與評價因子指標函數三維散點圖,如圖7所示.由圖7可知:越靠近左上角的離散點越優.根據權重值w1,w2及函數F1(x),F2(x)值,利用線性加權和公式F(x)=w1F1(x)+w2F2(x),最終可以求得評價因子指標函數F(x)值.

圖7 最短完工時間函數和總機器成本函數與評價因子指標函數三維散點圖

243種機器數量組合與相應評價因子指標函數二維散點圖,如圖8所示.由圖8可知:越靠上的點(函數F(x)值越大),其對應的并行機器數量組合越優.

圖8 243種機器數量組合與相應評價因子指標函數二維散點圖

評價因子指標函數對應的主要指標值,如表2所示.由表2可知:并行機器數量組合E=[2,3,2,50,1,1,6,3,1]的評價因子指標函數F(x)的值最大,也是雙目標優化問題的最優解,函數f1(x)的值為

表2 評價因子指標函數對應的主要指標值

54,函數f2(x)值為95.

最優機器數量組合下的最優調度方案甘特圖,如圖9所示.

圖9 最優機器數量組合下的最優調度方案甘特圖

4 結論

根據裝配式建筑的整個建造過程,分析研究預制構件在生產、運輸與裝配階段的具體工作流程,對各個階段的工作流程進行簡化,將預制構件全階段的工作流程簡化為9道工序.將預制構件調度優化作為一個擴展型的生產車間調度優化問題.在HFSP理論的基礎上,對預制構件全階段調度問題進行建模,對完工時間和并行機器的總機器成本進行優化.采用改進的遺傳算法對模型求解,改進后的遺傳算法更符合模型要求,并提高了搜索最優解的效率.

對預制構件生產-運輸-裝配全階段調度進行優化,打破以往研究中只考慮某一個階段的局限性,促進裝配式建筑更加經濟化、合理化、科學化.但也存在一些不足,如模型的約束多是基于多種理想化的假設,沒有充分考慮實際工程情況,以及在模型多目標優化時沒有優化其他成本.