基于CSI和K-means-SVR的多指紋庫室內定位方法

王 逸，裴生雷，2*，王 煜

（1.青海民族大學 物理與電子信息工程學院，西寧 810007；2.人工智能應用技術國家民委重點實驗室（青海民族大學），西寧 810007；3.天津大學 智能與計算學部，天津 300350）

0 引言

隨著新一輪智慧城市的興起，公眾Wi-Fi 作為一項惠民工程，幾乎普及到了我們周圍的各個角落。尤其是在旅游景點中，絕大部分都已經實現了Wi-Fi 全覆蓋，當游客的智能設備連接到景點的Wi-Fi 后，就能充分體驗景點的各種個性化服務，如地圖導覽、景點介紹、實時講解等。在游客享受更好服務的同時，景點也可以通過Wi-Fi 收集數據，包括每天服務人數、游客景點內軌跡分析、游覽時間喜好、享用服務頻次、游覽時長等。通過分析這些數據，可以大幅提高景點的服務質量和應急響應能力。與蜂窩信號相比，Wi-Fi 信號傳輸速率更快、成本更低，并且使用頻段在全球范圍內都不受限制［1］，所以景點全覆蓋的Wi-Fi 網絡將會受到更多游客的青睞。景點若想使用Wi-Fi 數據獲取游客的游覽軌跡、游覽時長、游覽喜好等數據，就要使用Wi-Fi 定位技術獲取游客的位置。雖然室外定位技術非常成熟，如北斗定位系統［2］和蜂窩定位系統［3］，都能實現非常精準的定位。但是，國內有許多重要的景點并不在室外，如故宮、兵馬俑、黃鶴樓等，還有全國各地的生態、文化景點，游客更加需要旅游導覽、實時講解等服務，所以更需要室內定位來確定游客的位置，為游客提供更好的服務。但室內定位技術發展并不迅速。與外部環境不同，室內環境因有許多障礙物，導致北斗衛星信號的強度在室內也會大幅下降；而且為了保護歷史古跡，許多古跡景點的蜂窩信號強度并不理想，尤其是在絕大部分Wi-Fi 覆蓋的景點，Wi-Fi 信號強度要遠強于蜂窩信號，所以在這些景點使用Wi-Fi 定位將會更加精準。

傳統的Wi-Fi 室內定位使用接收信號強度（Received Signal Strength Indication，RSSI）數據，相較于傳統的RSSI 室內定位［4-7］，信道狀態信息（Channel State Information，CSI）數據不僅在時間上具有穩定性，并且不同位置CSI 數據的特性變化明顯，因而受到了廣大學者的關注［8-10］。Wang 等［11］提出了RSSI 與CSI 相結合生成的混合指紋庫的定位方法。孟俊劍等［12］用序列最小優化（Sequential Minimal Optimization，SMO）算法建立降維特征與相應位置的回歸模型，并對位置進行預測。Dai 等［13］提出了基于K 近鄰（K-Nearest Neighbor，KNN）算法的CSI 室內定位，但是每次定位都需要在線和指紋庫的所有數據進行逐個對比匹配，定位效率不高。田廣東等［14］利用了CSI 成簇分布的特性，使用了K 均值（K-means）聚類算法對CSI 數據進行特征提取，然后使用KNN 算法定位。黨小超等［15］提出了CSI 的支持向量機（Support Vector Machine，SVM）回歸的室內定位方法。這些基于CSI 的室內定位方法都分為離線階段和在線階段，其中離線階段建立指紋庫［16］，在線階段進行指紋匹配，最終實現定位。Rao 等［17］提出了DFPhaseFL 系統，首先從信道狀態信息測量中提取原始相位信息，然后去除相位偏移，得到濾波后的校準相位信息，最后進行定位。然而，上述方法在兩個階段中采取的策略各有優缺點，尤其是離線階段都使用單指紋庫導致模型訓練復雜度提高；而在線階段，預測點數據需要與指紋庫中所有數據進行匹配，定位效率不高。

Wi-Fi 室內定位應用場景多樣，但是對于旅游景點等復雜場景下的應用，會受到時間段等因素的影響，導致人流量在不同時間、不同區域驟增或驟減。面對這些情況，傳統的室內定位方法因受單指紋庫的影響，無法充分利用系統資源。尤其是在線定位階段，使用傳統定位方法定位時需要與每個指紋點進行匹配，即使是閑置指紋點也要進行多次匹配，導致指紋庫運行緩慢、延遲較高、體驗較差。

本文將K 均值聚類算法與支持向量回歸（Support Vector Regression，SVR）算法相結合，提出了一種多指紋庫定位方法。根據不同位置CSI 信號的簇分布特點，將定位指紋點存入多個指紋庫，進而在多指紋庫中分別建立模型，實現位置預測。該方法不僅能提高定位精度，而且能有效提高定位效率，每次定位都無須與所有指紋庫中的數據進行匹配，可以把閑置的指紋庫所使用的系統資源分配給繁忙指紋庫，避免了系統資源的浪費。

1 指紋定位系統

在Wi-Fi 室內定位場景中，通過收集CSI 信息和對象位置坐標實現指紋定位系統，進而為用戶提供位置服務，滿足用戶在特殊場景下的位置需求。

根據指紋定位系統在不同場景的應用需求，本文提出的多指紋庫定位方法具體流程如圖1 所示。首先，基于CSI 成簇分布的特點，利用K-means 算法對訓練樣本進行聚類以獲取k個簇的CSI 數據，進而基于k個簇分別建立指紋庫；然后在k個指紋庫中分別訓練SVR 模型；最后，由SVR 進行位置精準預測。

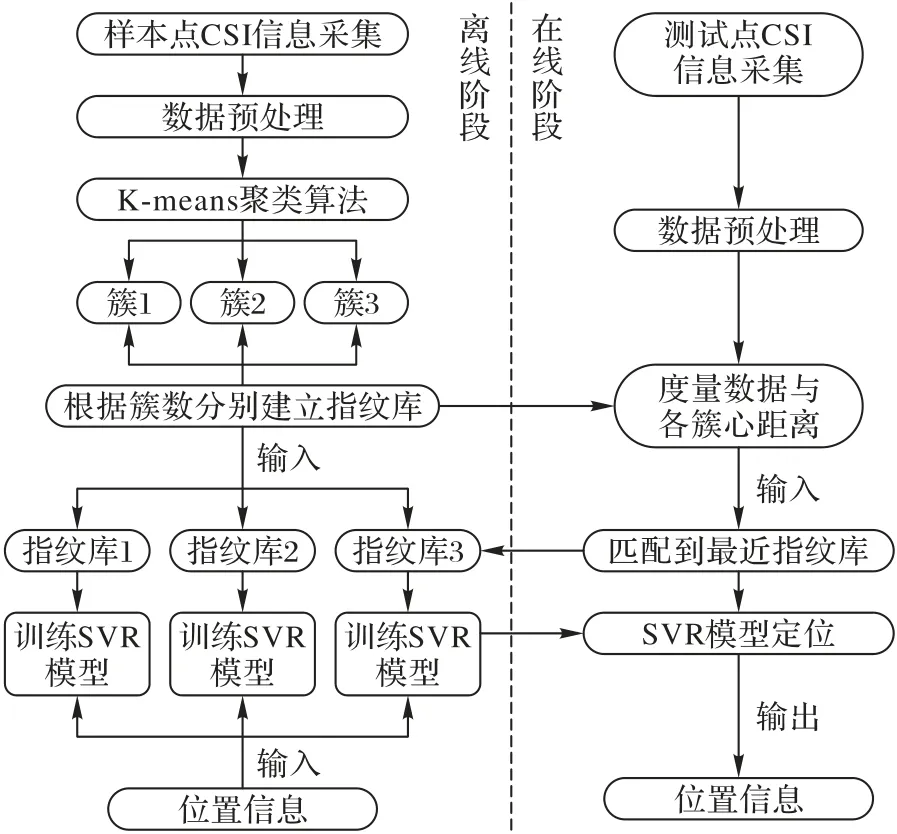
圖1 定位流程Fig.1 Flow of positioning

2 CSI原始數據處理

2.1 CSI數據描述

CSI 作為定位系統的數據源，其原始數據以復數矩陣的形式存在。采用CSI Tool［18］讀取CSI 數據，每個CSI 數據包所能提取的CSI 子載波個數為30，并可以用矩陣H表示CSI 信息。每個CSI 數據為p×q× 30，其中：p為發射天線數量，q為接收天線數量，子載波個數為30。

為了有效利用CSI 數據，通過數據結構分解得出相應的數據。將CSI 信號定義為：

若第k個子載波上的幅度表示為‖Hk‖，相位表示為∠Hk，那么每一個子載波上的CSI 可表示為：

由于相位信息受頻偏影響不能精確提取，本文方法僅提取幅值作為指紋信息：

CSI 的幅值在距離無線接入點（Access Point，AP）點不同的位置時，有不同的特性。如圖2 所示，橫坐標表示3 條鏈路的子載波索引，縱坐標為它們的幅值，3 條線代表3 根天線接收到的CSI 數據，當靠近AP 點位置測量CSI 數據，3 根天線的信號表現出了相似的特性；但當在距離AP 較遠的位置進行測量時，3 條鏈路的曲線不再相似，并且鏈路之間的差異性變大；即使是同一條鏈路，幅值也有很大的變化，這說明CSI幅值對于位置的變化非常敏感。

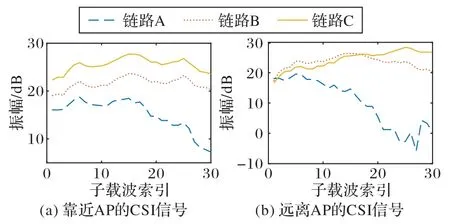
圖2 靠近和遠離AP的CSI信號Fig.2 CSI signals close to AP and away from AP

2.2 數據預處理

采集數據后會生成一個樣本維度為Ntx×Nrx×N的CSI數據，其中：Ntx為發射天線數，Nrx為接收天線數，N為子載波數量。由于原始數據中有1 根發射天線、3 條鏈路，每條鏈路上的子載波數量為30，所以每個CSI 信號的維度為1×3×30。為了獲取有效的高維信息，使用主成分分析（Principal Component Analysis，PCA）算法將數據的N維信息通過線性變換投影到K1維空間中，其中N維是數據本身的維度，K1維是低維。通過該方法，實現了Ntx×Nrx×N列的數據降維，獲取了有效的CSI 信息，保證了數據質量。

3 結合K-means和SVR的定位方法

3.1 基于CSI數據簇分布特點的聚類分析

依據文獻［19］的實驗分析，CSI 數據呈現成簇分布的特點，并且認為超過80%的CSI 幅值向量只存在4 個以內的分簇。因此考慮應用K-means 算法實現CSI 數據分簇，該算法采用距離來衡量樣本之間的相似性，將降維后的CSI 數據劃分成k個簇，其中，μi是簇Ci的均值向量：

K-means 算法的本質就是尋找k個質心來最小化平方誤差E，E越小說明數據相似度越高，將CSI 幅值相似度較高的樣本進行聚簇。

3.2 建立多指紋庫

經過K-means 得到k個類別，構建k個指紋庫[R1，R2，…，Rk]，每個指紋庫包含F個樣本的CSI 指紋。設F={r1，r2，…，rn}，n是指紋信息的個數，CSI 數據經過PCA 降維后，指紋屬性集為[λ1，λ2，…，λi]。將F個樣本包含的CSI指紋屬性分別與坐標對應，對應坐標P={(x1，y1)，(x2，y2)，…，(xn，yn)}，對 應后建 立多指紋庫[R1，R2，…，Rk]，其中：

3.3 構建基于多指紋庫的SVR模型

建立多個指紋庫后，每個指紋庫里都存入了不同位置的CSI 樣本數據，然后在每個數據庫中分別建立SVR 回歸模型進行定位。基于SVR 回歸算法的核心思路在于用回歸的想法找出CSI 幅值和位置的關系［20］。在高維空間中，用非線性映射的方法尋找一個最優超平面，以此來替換原本的非線性關系。

建立了k個指紋庫后，分別使用每個指紋庫的數據集，{(ri，xi)|i=1，2，…，n} 和{(ri，yi)|i=1，2，…，n}。基于SVR 算法，利用CSI 的幅值信息與坐標信息的關系，建立函數fx和fy。在x軸上建立線性回歸估計函數：

其中：w為權值向量；φ(r)將低維度的CSI 指紋信息映射到高維空間；b是定值。

SVR 的標準形式為ε-SVR，其中ε為不敏感損失函數。SVR 的風險泛化函數R(w)如式（9）所示，其中CSIam是幅值的特征信息。

確定參數w和b時為了損失最小，所以解決最優化問題可化為：

約束條件為：

其中：αi表示拉格朗日乘子。由式（14）得到x軸坐標的計算函數，y軸同理。通過這種方法，在多個指紋庫中訓練出不同的SVR 回歸模型，進行位置預測。

3.4 利用SVR模型實現位置預測

基于SVR 模型的位置預測過程：首先在測試點收集CSI指紋信息，然后進行指紋信息預處理；接著與離線階段K-means 生成的簇心作距離度量，進而將測試點歸入最相似的指紋庫中；最后利用離線階段所訓練的SVR 模型進行預測，分別預測出x軸與y軸的位置坐標。

當預測位置與本身位置不同時，即存在誤差，設預測點坐標為(x，y)，實際坐標為(x1，y1)，預測點坐標與實際坐標直線距離為Dis，如式（15）所示，用兩坐標的直線距離來表示誤差。

4 實驗與結果分析

4.1 實驗設置

本文提出的多指紋庫室內定位方法面向實驗室場景進行實驗分析與驗證。該實驗室長8 m，寬6 m，將實驗參考點劃分標記為0.6 m×0.6 m 大小的方格，采集12 個點的位置坐標與CSI 數據，位置平面圖如圖3（a）所示，其中位置5、6、7、8與位置9、10、11、12 中間有一堵墻作為障礙物。

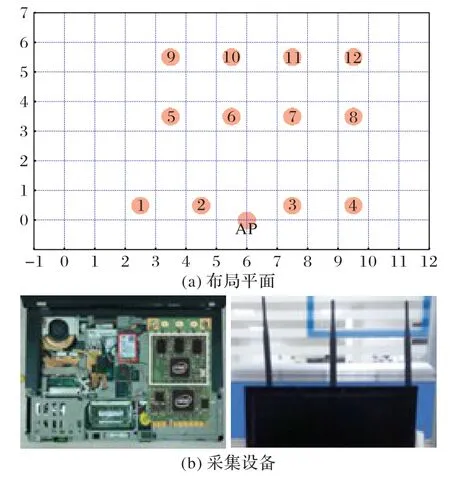
圖3 實驗環境的布局平面以及采集設備Fig.3 Layout plan and acquisition equipment of experimental environment

在實驗中，數據采集階段使用3 臺聯想ThinkPad T400 筆記本電腦作為顯示器，如圖3（b）所示。每臺筆記本電腦都運行32 位Ubuntu Server 10.04（LTS）操作系統，并配置了Intel 5300 802.11n 無線網卡。AP（或監視器）使用在2.4 GHz 頻段的通道6 上運行的接口wlan0 與用戶通信，使用接口eth0 與服務器通信。服務器使用eth1 連接到Internet。數據處理階段采用筆記本電腦的CPU 為Core i7-11800H@2.30 GHz，操作系統為Ubuntu 20.04.3。

4.2 實驗分析

為了驗證本文算法在不同實驗環境中的定位誤差以及定位效率，設計了不同參考點數量的誤差分析實驗與不同算法的誤差分析實驗。采用累積分布函數（Cumulative Distribution Function，CDF）圖來表示定位誤差的大小，并利用定位誤差累計概率分布和平均誤差對實驗結果進行評價。

4.2.1 不同參考點數量誤差分析

為了驗證不同樣本數對本文算法性能的影響，分別測試了在100、300、700 個樣本點情況下的定位誤差，使用CDF 圖表示在不同樣本數量情況下的誤差，如圖4 所示，在樣本數為700 時的平均誤差為0.95 m，樣本數為300 時的平均誤差為1.8 m，樣本數為100 時的平均誤差為2.1 m。

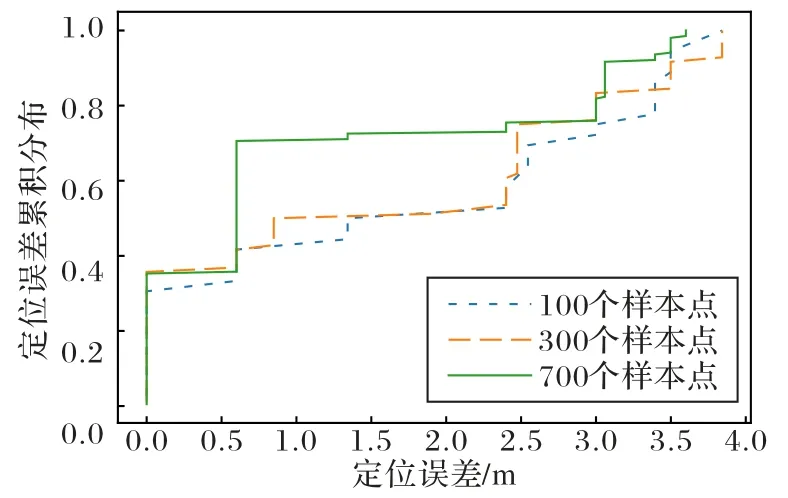
圖4 不同樣本數量的CDF圖Fig.4 CDF diagram of different sample numbers

4.2.2 算法性能比較

為了驗證本文算法的性能，分別與文獻［15］提出的SVR算法、傳統的單指紋庫的KNN 回歸算法、支持向量分類（Support Vector Classification，SVC）算法以及DFPhaseFL 系統作比較。實驗在樣本數量為700 的情況下計算了定位誤差的累積分布，如圖5 所示。從圖5 可以看出，本文提出的K-means-SVR 算法在定位誤差為0.6 m 以下的百分比達到了35%，定位誤差在1.2 m 以下的百分比達到了70%，平均精度為0.95 m，明顯優于其他四種算法。

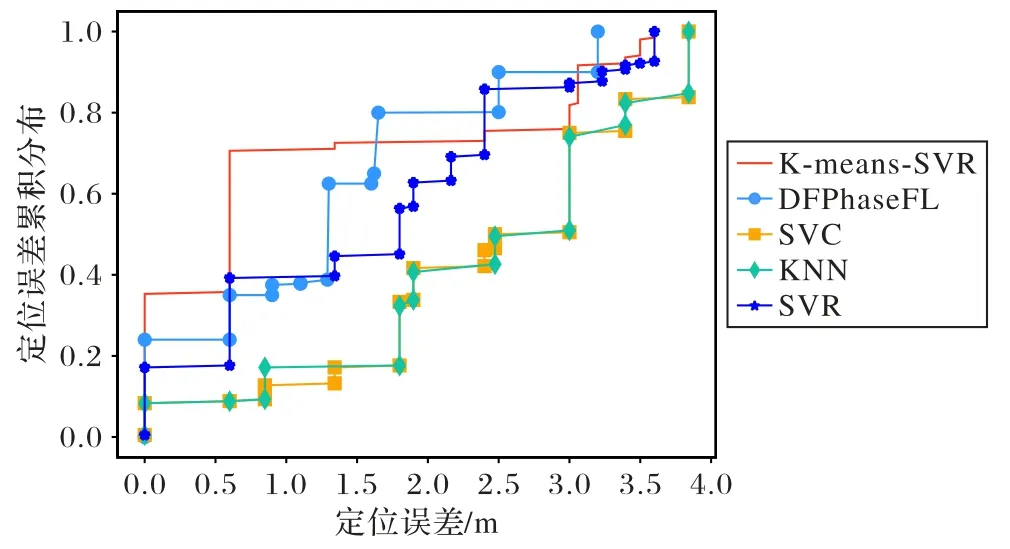
圖5 定位算法誤差比較Fig.5 Error comparison of positioning algorithms

從表1 中可以看出，本文提出的K-means-SVR 算法在定位誤差為［0，0.6］ m 時的概率為35%，定位誤差在［0，1.2］ m的概率為70%，定位誤差明顯小于其他四個算法。同時，定位誤差在［0，4］ m 的范圍時K-means-SVR 算法的平均誤差最小，達到了0.95 m。可見本文的K-means-SVR 算法相比文獻［17］所提出的DFPhaseFL 系統、文獻［15］所提出的SVR 算法以及傳統的SVC、KNN 算法，在性能上有了顯著的提高。

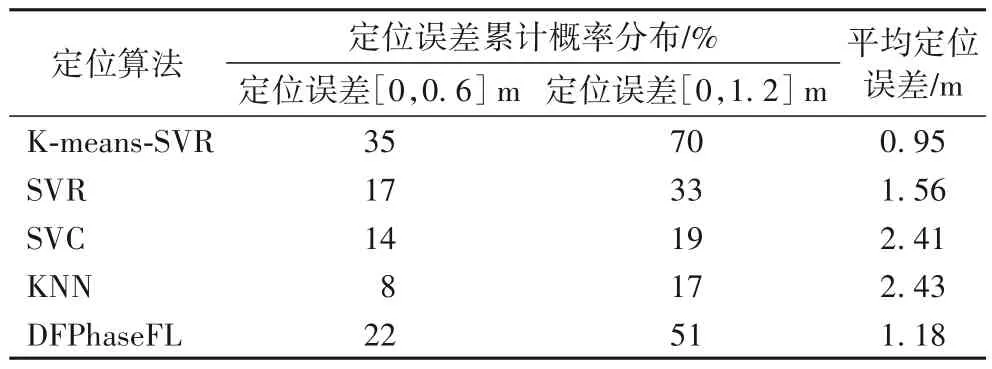
表1 樣本數量為700時不同定位算法的性能對比Tab.1 Performance comparison of different positioning algorithms when sample unmber is 700

5 結語

本文提出了一種基于CSI 的多指紋庫定位算法，在CSI數據成簇的特性上，將樣本聚為3 類，分別建立指紋庫，再用SVR 進行預測，不但提高了定位的精準度和定位效率，而且解決了人流量驟增導致定位精度下降、定位緩慢、閑置定位點多次匹配進而造成內存浪費等問題。然而，該算法僅僅使用了CSI 的高維信息，并未充分挖掘CSI 的低維信息。因此，下一步將充分利用CSI 的低維信息結合高維信息，探索動態環境下Wi-Fi 室內定位方法。