反復有常——生活中的反比例

陳熙嫄

可以用反比例函數模型刻畫的生活現象常因現實問題中“非負數”的限制而導致相關問題對應的都是雙曲線在第一象限的情形——因變量隨著自變量的增大而減小、隨著自變量的減小而增大，簡直就是“反復無常”.但只要掌握了反比例函數的性質，“無常”變“有常”也是易事，下面一起欣賞3例.

一、表格“單打”

例1（2022·湖南）科技小組為了驗證某電路的電壓U（V）、電流I（A）、電阻R（Ω）三者之間的關系：I=U/R，測得數據如下：

R/Ω 100 200 220 400

I/A 2.2 1.1 1 0.55

那么，當電阻R=55Ω時，電流I=_____A.

解析：表格法呈現的函數關系對應數值準確明晰，但不利于計算表格內尚未包含的自變量或因變量的值.因此，需要借助表格內自變量與因變量的對應關系求出函數解析式.把R=220，I=1代入I=U/R得：1= U/220，解得U=220，∴I=220/R，把R=55代入I=220/R得：I=220/55=4，故填4.

點評：函數關系有三種基本形式，要善于識別并因勢、因需靈活轉換才行.本題是一道簡單的反比例函數應用題，題目給出的“I=U/R”即鎖定了I與R之間的反比例關系，由表格數據求出反比例函數的解析式，再代入求值即可. 小技巧：選取計算量小的一對自變量和因變量數值進行計算.

二、圖象“單打”

例2（2022·廣東）某燃氣公司計劃在地下修建一個容積為V（V為定值，單位：m3）的圓柱形天然氣儲存室，儲存室的底面積S（單位：m2）與其深度d（單位：m）是反比例函數關系，它的圖象如圖所示.

（1）求儲存室的容積V的值；

（2）受地形條件限制，儲存室的深度d需要滿足16≤d≤25，求儲存室的底面積S的取值范圍.

解析：用圖象法表示函數的優點是形象直觀，能夠清晰呈現函數的增減變化，不足之處是所畫出的圖象是近似的、局部的，觀察的變量值往往不夠準確，而這恰恰是解析式可以清晰表示的.

（1）設解析式為S=V/d，只需借助“一點”（20，500）即可求出V的值為10000（m^3）；

（2）借助反比例函數的性質因變量S隨著自變量d的增大而減小，并結合“界點”（16，S1）和（25，S2）就可以求出S的范圍為400≤S≤625.

點評：通過函數關系把三種表示方法結合起來，揚長避短，優勢互補.解答本題的關鍵是確定反比例函數解析式，再根據函數解析式，計算“界點”，并結合反比例函數變量之間的增減變化解決相關問題.

三、圖表“混雙”

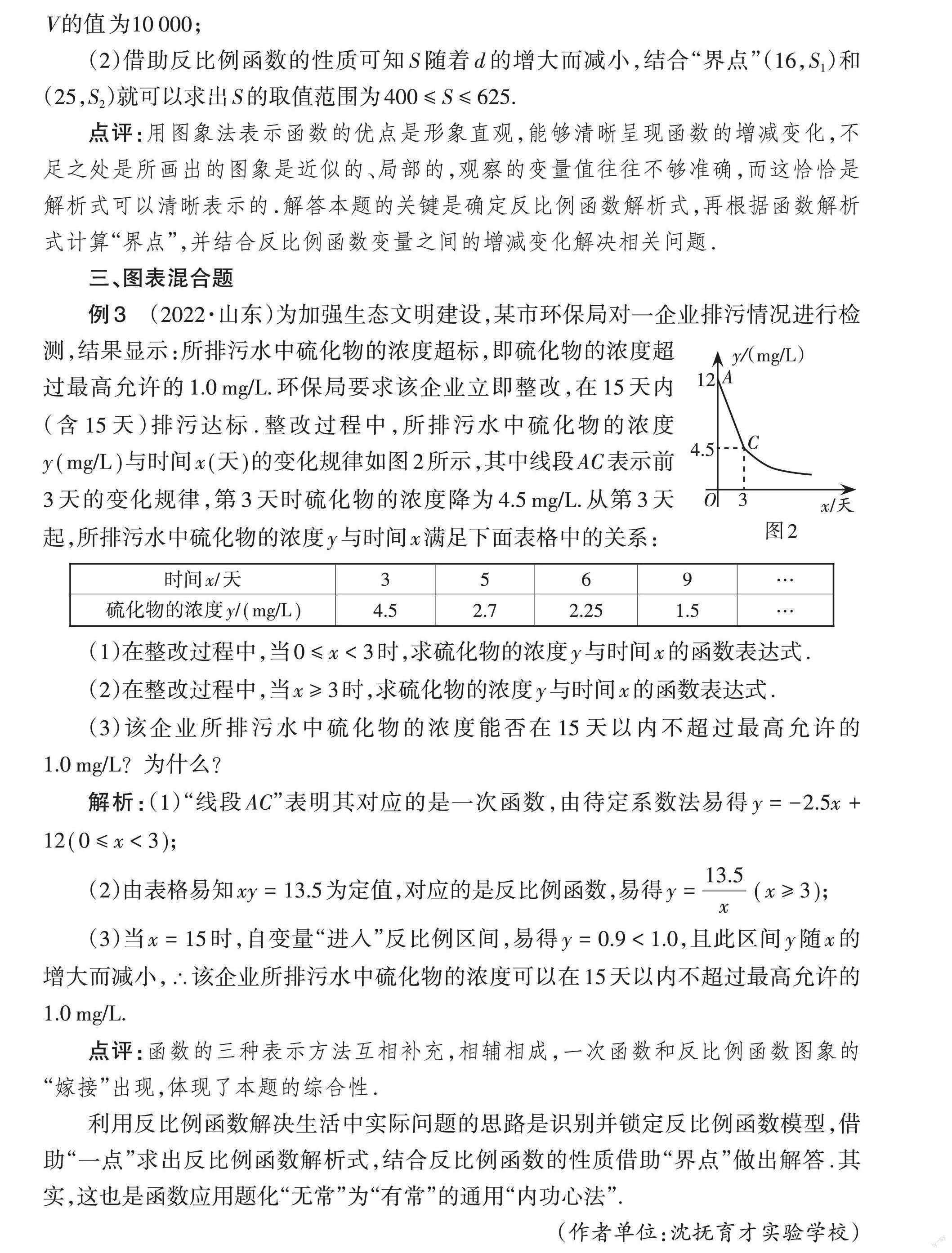
例3（2022·山東）為加強生態文明建設，某市環保局對一企業排污情況進行檢測，結果顯示：所排污水中硫化物的濃度超標，即硫化物的濃度超過最高允許的1.0mg/L.環保局要求該企業立即整改，在15天內（含15天）排污達標.整改過程中，所排污水中硫化物的濃度y（mg/L）與時間x（天）的變化規律如圖所示，其中線段AC表示前3天的變化規律，第3天時硫化物的濃度降為4.5mg/L.從第3天起，所排污水中硫化物的濃度y與時間x滿足下面表格中的關系：

時間x/天 3 5 6 9 …

硫化物的濃度y/（mg/L） 4.5 2.7 2.25 1.5 …

（1）在整改過程中，當0≤x<3時，硫化物的濃度y與時間x的函數表達式；

（2）在整改過程中，當x≥3時，硫化物的濃度y與時間x的函數表達式；

（3）該企業所排污水中硫化物的濃度能否在15天以內不超過最高允許的1.0mg/L？為什么？

解析：函數的三種表示方法互相補充，相輔相成，一次函數和反比例函數圖象的“嫁接”出現，體現了本題的綜合性.

（1）“線段AC”表明其對應的是一次函數，由待定系數法易得y=-2.5x+12（0≤x<3）；

（2）由表格易知x?y=13.5為定值，對應的是反比例函數，易得y=13.5/x（x≥3）；

（3）當x=15時，自變量“進入”反比例區間，易得y=0.9<1.0，且此區間y隨x的增大而減小，∴該企業所排污水中硫化物的濃度可以在15天以內不超過最高允許的1.0mg/L.

點評：本題的第一道“待越龍門”是從函數的圖象和表格中提取信息逆向判斷函數類型，進而求函數解析式；第二道“待越龍門”是因自變量“分段”對應不同的函數關系，需要判斷自變量所在區間，提高了綜合性；第三道“待越龍門”是反比例函數的性質運用.題目的綜合性塑造了作答者的“神勇無敵”！

利用反比例函數解決生活中實際問題的思路是識別并鎖定反比例函數模型，借助“一點”求出反比例函數解析式，結合反比例函數的性質借助“界點”做出解答.其實，這也是函數應用題化“無常”為“有常”的通用“內功心法”.

（作者單位：沈撫育才實驗學校）