帶支撐物真空玻璃的四點彎曲實驗數值分析＊

劉慶雨，王其遠，李嘉新，班宇恒，王彥生

（1.河南科技大學土木建筑學院，河南 洛陽 471023；2.河南科技大學車輛與交通工程學院，河南 洛陽 471023）

隨著建筑、汽車、裝飾裝修和家具等其他行業的發展和人們對生活空間環境要求的提高，安全玻璃、節能真空玻璃等功能性加工產品得到廣泛應用。真空玻璃利用保溫水杯原理，基本消除了因空氣傳導和對流而引起的熱傳輸，提高了玻璃構件的隔熱性能。另外，真空玻璃還具有防結露結霜、抗風壓、隔聲等功能。因此，真空玻璃是繼單片玻璃、中空玻璃后，備受國際推崇的第三代節能建筑材料，是近期和未來玻璃領域重要發展的戰略材料之一[1]。

帶支撐物的真空玻璃以2塊鋼化玻璃基板為主體，在2 塊玻璃之間放置支撐物，再將玻璃中間抽成真空狀態，并進行嚴格的密封。因帶支撐物的真空玻璃具有復雜的制作工藝，所以在制作中存在著很多技術難關[2-3]，比如在玻璃板的制造中要選擇合適的真空度和封接方式，在支撐物的選擇和排布方式上也有許多問題需要考慮[4]。因此，對帶支撐真空玻璃結構的強度分析[5-7]等方面進行研究是十分重要的。

通過理論分析、數值模擬和實驗驗證的方法，探索合理的結構設計，優化真空玻璃內部應力，降低環境溫度、風載荷、振動及沖擊載荷等作用對真空玻璃的不利影響。針對強度分析和應力誘導真空玻璃破裂的問題，英國ULSTER 大學的SIMKO 等[8]構建了含有支撐和封邊的完整有限元模型，分析了低溫封邊技術在真空玻璃內部產生的應力；WULLSCHLEGER 等[9]采用3 種不同類型的鋼化真空玻璃模型，研究了支撐物對鋼化真空玻璃橫向剪切剛度和撓度的影響；藺海曉等[10]采用赫茲接觸理論，對鋼化真空玻璃球形支撐壓痕應力場進行了分析；蔡冬等[11]基于彈性理論和ANSYS 分析了支撐物缺位對弧面鋼化真空玻璃支撐應力的影響；李彥兵等[12]分析了支撐點間距對鋼化真空玻璃力學特性的影響；劉小根等[13-15，3]對真空玻璃的支撐壓痕控制準則、溫差作用應力、風壓作用應力、支撐物缺位影響、真空玻璃結構優化及工程應用理論等方面也進行了較詳細的探討，有力支撐了真空玻璃新產品研發及其結構優化與工程應用。但以上分析結果均未涉及實驗驗證方法，從而忽視了真空玻璃在實際載荷作用下的強度分析及全場變形。

本文基于Solidworks 與ANSYS Workbench 建立帶支撐真空玻璃有限元分析模型，模擬真空玻璃在四點彎曲實驗時的工況并以此確定真空玻璃在四點彎曲工況下的危險部位。根據數值模擬結果來確定實際加載時的載荷大小，以防實驗對真空玻璃造成損害而影響后續實驗。首先運用電測法和數字圖像相關技術（DIC）方法來測量受壓彎曲工況下的應變，通過對比實驗測定結果與數值模擬結果，驗證本文有限元分析模型的準確性與可靠性；接著以數值模擬的方式，通過改變玻璃夾層之間的支撐柱厚度與半徑來獲取四點彎曲時的危險部位應力值，并以此數據進行多元線性擬合，建立多目標規劃數學模型來求得危險部位最小應力值所對應的支撐柱厚度與半徑。

1 有限元靜力學分析

1.1 真空玻璃物理模型的建立

1.1.1 平面幾何模型與三維模型的建立

真空玻璃由2 片平板鋼化玻璃構成，邊緣用低熔點玻璃粉密封，玻璃基板厚度為6 mm、尺寸為1 100 mm×360 mm；中間用材料為低碳鋼的支撐物隔開，其直徑為0.5 mm，高為0.3 mm，間距為60 mm×50 mm。真空玻璃幾何模型示意簡圖及支撐柱分布情況如圖1 所示。

圖1 真空玻璃幾何模型示意簡圖及支撐柱分布情況

基于SolidWorks 建立四點彎曲實驗所對應的三維幾何模型，如圖2 所示。其中2 根支撐輥被固定在拉伸試驗機的底座；2 根壓輥被固定在下夾頭，用于四點彎曲實驗時加載。支撐物為圓柱狀，分布于2 層玻璃之間。

圖2 四點彎曲工況下的實體模型

1.1.2 材料屬性設置

材料屬性參數的選取按照行業標準JGJ 102—2003《玻璃幕墻工程技術規范》，具體材料屬性參數如表1所示。

表1 實驗材料屬性

在圖2 的四點彎曲工況下的實體模型中，2 塊玻璃板的材料為鋼化玻璃，2 根壓輥與2 根支撐輥的材料均為低碳鋼，2 塊玻璃之間的支撐柱材料同樣為低碳鋼。密封帶由玻璃粉制成，其材料屬性與鋼化玻璃相同。

1.1.3 邊界條件設定

通過對有限元分析模型設定合適的邊界條件來模擬真空玻璃在受壓彎曲時的實際加載工況，進而得出相應的數值仿真結果，其邊界條件的設定如圖3 所示。考慮到實際加載時2 根壓輥與2 根支撐輥并未出現與基片玻璃表面滑移的現象，故將4 根輥的表面分別與基片玻璃的外表面設定為綁定。

圖3 邊界條件的設定

1.1.4 網格劃分

作為有限元仿真的前處理技術，網格劃分是一個極其重要的步驟。六面體網格在計算精度、變形特性及網格數量上比四面體網格具有明顯的優勢。因此，在網格劃分時對所有模型均進行六面體網格劃分，并在主要關注部位降低網格尺寸來提高計算的精確性。對研究對象進行網格劃分的結果如圖4 所示。

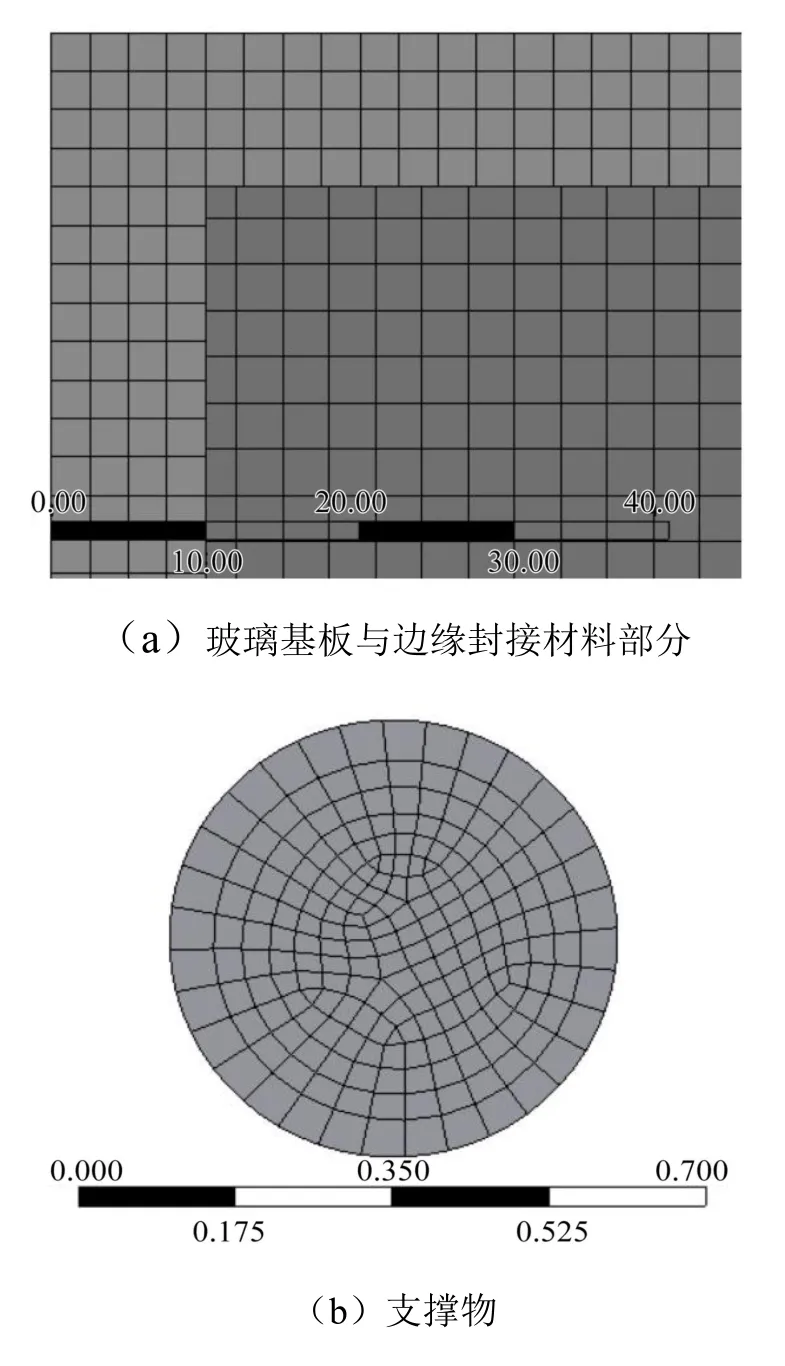
圖4 網格劃分結果（單位：mm）

1.2 四點彎曲工況下的數值模擬

在進行真空玻璃四點彎曲工況下的數值模擬時，結合1.1.3 中的邊界條件設定情況，對上部2 個壓輥設定向下300 N 的壓力約束，以模擬真空玻璃所受的四點彎曲工況。

四點彎曲工況下的數值模擬等效應力結果如圖5所示，并已標記上下玻璃基板外表面的危險部位處的等效應力值。由于真空玻璃結構具有很強的對稱性，因此圖5 僅展示玻璃基板50%的等效應力云圖。基于ANSYS Workbench 的數值模擬，確定了真空玻璃在四點彎曲加載工況下的支撐物所對應的外表面危險部位，并已標記出危險部位和該部位的等效應力值。

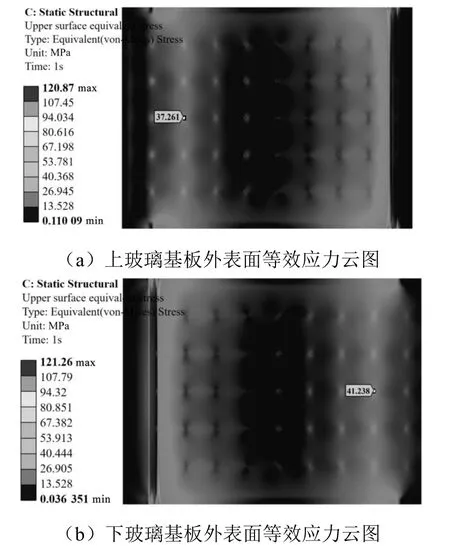
圖5 玻璃基板等效應力云圖

在圖5（a）中可以看出，中部壓輥與上部玻璃基板接觸的地方存在較大的應力，這是2 個剛性體在相互擠壓時所產生的正常現象，下玻璃基板（如圖5（b）所示）亦如此。除去接觸部位的接觸應力以外，上玻璃基板在四點彎曲工況下的危險部位在第二列第三行的支撐物位置處，下玻璃基板的危險部位在第八列第三行的支撐物位置處。

2 實驗結果與分析

2.1 電測與數值模擬結果對照

在對帶支撐真空玻璃成品的受力情況進行了有限元靜力學計算后，得到了有關應變、應力及位移的云圖。繼而在實驗室進行實際操作分析，將數值模擬結果與實際實驗結果進行比較并相互驗證，檢驗數值模擬的準確性。對帶支撐真空玻璃成品整體結構進行基于電測法和DIC 方法的受壓彎曲實驗，確定真空玻璃在受到特定載荷下的應變、應力及位移的分布情況。

電測法是利用電阻應變片測定被測物表面的應變，在實驗中所使用的應變片由敏感柵、基底和覆蓋層及引線這些部件組合而成，其中敏感柵是其結構的主要部分，在本質上相當于一個電阻，當實驗構件在載荷下發生變形時，敏感柵的電阻值也會發生變化，進而將應變信號，轉變為可以輸出的電信號并通過設備輸出應變數值。由于應變片對實驗環境的溫度變化十分敏感，并且電流的熱效應會影響應變片的測量值，所以為了更加準確地測量實驗構件的應變，排除熱誤差對電阻值的影響，所以在實驗中采用1/4 橋路分析，添加溫度補償片。

在真空玻璃受壓的過程中，玻璃基板會發生彎曲變形并產生應變。由于加載設備會影響光測對真空玻璃正中央部位視線的采集，所以貼片位置選擇真空玻璃正中央部位，在上下玻璃基板正中央部位各貼1 片應變片。對數值模擬結果與電測數據進行對比，相互驗證。

在電測法試驗過程中，每加載30 N 記錄一次應變儀所顯示的數據，最終加載至300 N，共計錄10 次實驗數據。為減小誤差，進行3 次實驗，并取3 次實驗結果的算術平均值作為最終實驗數據，如圖6 所示。

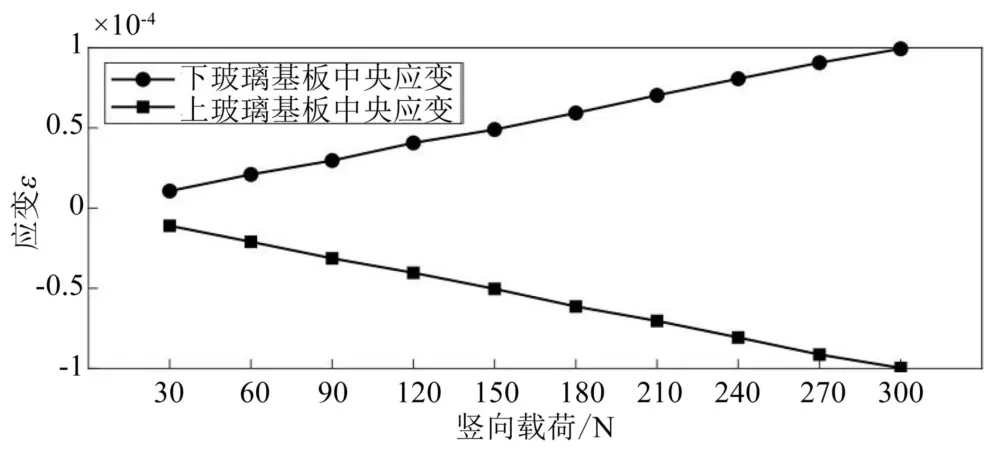
圖6 基于電測法真空玻璃中央應變數據

基于3 次實驗數據分析其誤差范圍，選取出同一載荷下的最大應變量與該載荷下的算術平均值進行比對，作為上極限偏差ξmax，其計算公式為：

將式（1）中的最大應變值轉換為最小應變值即得下極限偏差，分別對上下玻璃基板中央應變求上極限偏差與下極限偏差，其偏差范圍如圖7 所示。從圖7（a）可以看出，在剛開始加載時，有2 處的實驗數據極限偏差大于5%，但隨著載荷增大，數據的偏差變小并逐漸趨于0；在圖7（b）中，所有數據點的極限偏差均小于5%。

圖7 電測實驗數據偏差

在數值模擬中提取上下玻璃基板的中央應變，由于應變片的長度為6 mm，故提取以正中央為中心左右各3 mm 的3 處應變，用其算術平均值代替該應變片所測位置的平均應變，其數值模擬結果如圖8 所示。

圖8 玻璃基板中央部位應變數值模擬

綜上可知，電測法測得上玻璃基板中央在壓輥下壓300 N 時的應變為-99.7×10-6，數值模擬出的上玻璃基板中央平均應變為-101.96×10-6；下玻璃基板中央在壓輥下壓300 N 時的應變為99.3×10-6；數值模擬出的下玻璃基板中央平均應變為98.78×10-6，理論計算與實驗結果基本一致，誤差分別為2.27%和0.52%。

2.2 光測與數值模擬結果對照

該測量系統主要由CCD 攝像機、高速圖像采集卡、光源和計算機組成。利用數學相關方法分析受荷載作用下試樣表面數字圖像，將表面隨機分布的散斑點數據記錄在數字圖像中，利用數字圖像的灰度值模式來精確測定變形與位移。該方法具有與被測物體不接觸的優點。利用電測法測量實驗對象的應變時，需要在被測物體表面粘貼應變片，如果被測物體的剛度較小容易發生變形，粘貼應變片可能會對局部的剛度造成影響。而利用DIC 方法不直接與被測試件接觸，可以更準確地測量物體的應變情況。該方法測量范圍較廣，可以測試較大被測物體、較大測量范圍內的全場應變與變形情況。

散斑制作是DIC 方法測試的關鍵步驟，散斑質量較好可以提高物體表面特征點的識別度，影響實驗測試的結果。由于玻璃板表面較為平整，根據所測量范圍的尺寸，利用散斑工具印制散斑，以提高散斑質量。在預分析建立標定模板時，通過降低標定誤差并提高干擾因素水平進一步地提高實驗測量精度。標定誤差得分為0.038，該數值小于0.1，接受該標定模板。以圖1 左下角為原點（0，0），選取以點（250，160）和點（290，200）為頂點的正方形區域為數值模擬與光測實驗所測試部位。DIC 光測法所測出的形變云圖如圖9 所示，數值模擬結果如圖10 所示。

圖9 DIC 測試該區域的形變

圖10 數值模擬測試該區域的形變

由圖9 與圖10 可以得出，由實驗得出該區域的最小豎向位移為1.632 mm，數值模擬結果為1.614 7 mm；最大豎向位移為1.9 7 6 m m，數值模擬結果為1.971 mm，理論計算與實驗結果基本一致，誤差分別為1.06%和0.25%。

通過電測與光測實驗對真空玻璃有限元分析模型的驗證，得出了數值模擬結果與實驗結果吻合較好，從而驗證了有限元分析模型具有一定的可靠性，為后續的結構優化設計奠定基礎。

3 應力多元關系可視化

通過靜載與四點彎曲加載工況的實驗驗證，運用本文所建立的有限元分析模型對真空玻璃的結構設計進行優化。以真空玻璃基板之間的間隙與支撐柱直徑為優化對象，探索真空玻璃在不同結構設計下的力學性能。

通過不同的支撐柱厚度與支撐柱半徑的組合，探究上下玻璃基板內外表面的等效應力變化情況。將支撐柱的厚度設定為以0.05 mm 為步長，0.20～0.40 mm 這5種類型；將支撐柱的半徑設定為以0.05 mm 為步長，0.15～0.50 mm 這8 種類型。通過這40 種配合，探究了上下玻璃基板內外表面等效應力的變化情況。在1.2.2 中的有限元模擬結果中，將已確定的危險部位作為本章節主要探究的2 個部位，并通過加厚此部位的網格厚度來獲取更精確的結果。提取了40 種配合下的危險部位處最大等效應力值，并將此展示在可視化熱圖中，如圖11 和圖12 所示。

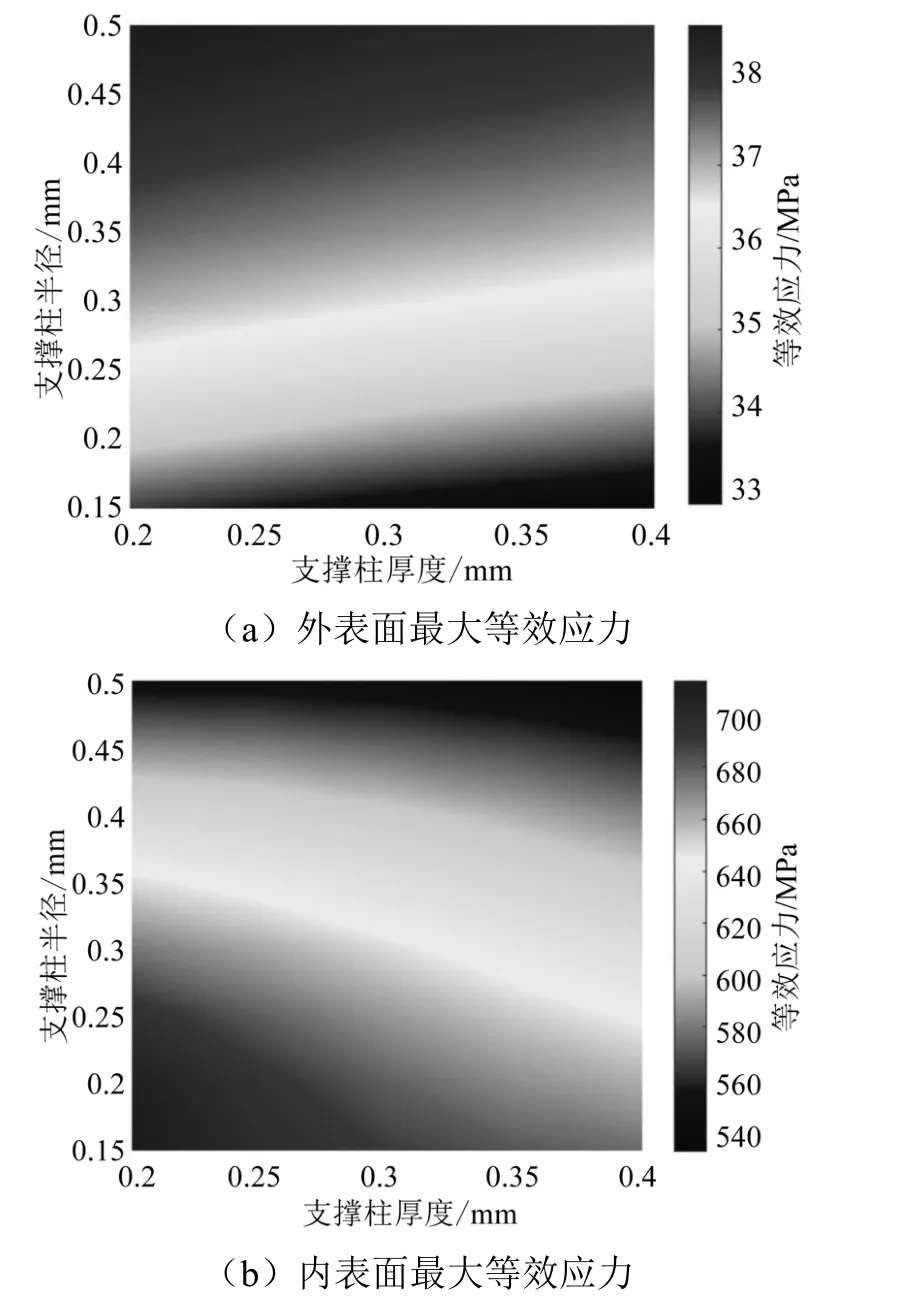
圖11 上玻璃基板危險部位等效應力變化趨勢

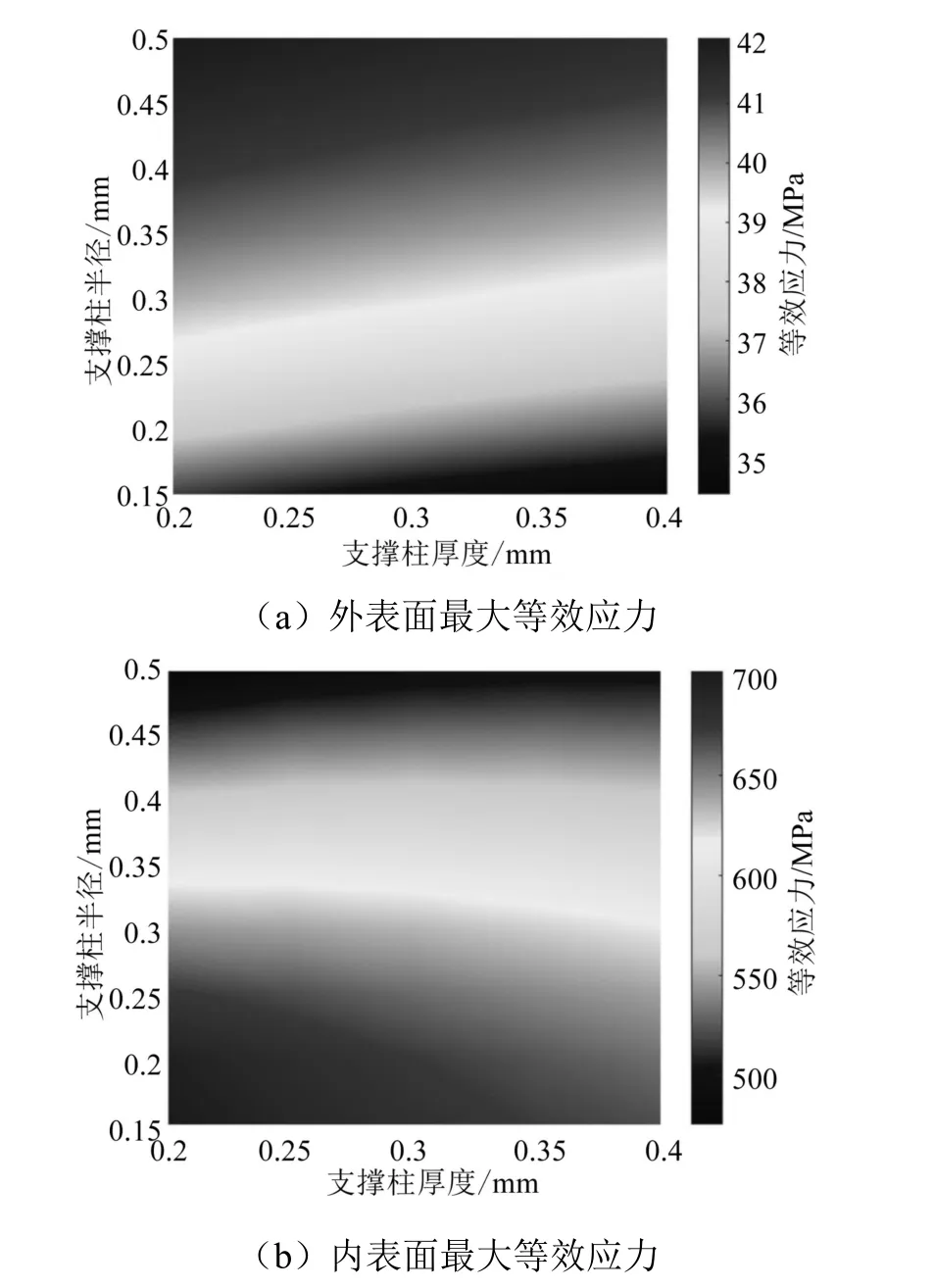
圖12 下玻璃基板危險部位等效應力變化趨勢

從圖11（a）與圖12（a）中可以看出，當支撐柱半徑固定時，上玻璃基板外表面危險部位等效應力值隨著支撐柱厚度略有減小；從熱圖條紋上來看，該減小趨勢基本不隨支撐柱半徑的變化而變化。從圖11（b）中可以看出，當支撐柱半徑固定時，上玻璃基板內表面危險部位等效應力值依然隨著支撐柱厚度而減小，但該減小程度隨著支撐柱半徑的減小而增大。而在圖12（b）中可以看出，當支撐柱半徑較大時，下玻璃基板內表面最大等效應力基本不隨支撐柱厚度的變化而變化；但在支撐柱半徑較小時，該等效應力值隨著支撐柱厚度的增大而減小。

4 結論

基于本文所研究的真空玻璃模型，探究了真空玻璃結構在靜載與風載工況下的變形云圖及等效應變云圖。支撐柱連線交點位置的變形最大，而支撐柱位置處的等效應變較大。

基于本文所建立的有限元分析模型，改變支撐柱的厚度及半徑來探究最佳的力學性能表現。通過分析熱圖及其條紋分布方式，在四點彎曲工況下，玻璃基板外表面危險部位等效應力值隨著支撐柱厚度略有減小，且該減小趨勢基本不隨支撐柱半徑的變化而變化。