新時代小學數學創新思維能力提高的策略

☉達瓦卓瑪

數學是一門具有較強抽象性與邏輯性的教學學科，無論是最為基礎的數學公式、數學概念，還是難度較大的數學問題、數學思想方法無一不指向著學生思維能力的發展提升。因此，在現如今的小學數學課程教學中，采取恰當、合理的教學手段與技術方法對數學教學模式進行合理的優化改革，將更多眼光聚焦在學生思維品質的提升之上，不僅有利于教學質量的本質性提高，于學生數學核心素養的發展、思維能力的進階也有著非比尋常的重要作用與積極影響。

一、注重知識關聯，為創新思維的生長夯實基礎

學生創新能力與創造思維的發展形成是建立在豐富的知識基礎之上的。［1］所以，在教學中，為讓學生通過數學課程教學實現對數學知識的舉一反三、觸類旁通，教師就必須要將“積土成山，風雨興焉；積水成淵，蛟龍生焉”的思想觀念深深植根于課堂教學之中，并要基于數學學科知識之間所存在的密切關聯性，引導學生展開追本溯源的深度數學學習，從而在有效驅動學生完善數學知識體系建立形成的同時，更好地滋養學生的創新思維能力，促進學生思維品質的進階。

以人教版小學數學四年級下冊教材為例，如在引導學生學習《三角形》一課后，教師就可鼓勵學生以小組合作的形式對本課所學知識內容進行梳理鞏固，構建以“三角形”為核心關鍵詞的數學思維導圖。

在《三角形》一課中，學生掌握了三角形的特性、三角形的基本構成、三角形的分類、三角形內角和等基礎幾何數學知識，對三角形這一簡單幾何圖形形成了較為全面的認識把握。為讓學生的數學學習認識上升新高度，得到思維的發散與活躍，教師在引導學生繪制“三角形”思維導圖時，就要著重關注上述知識內容之間的邏輯關系。

首先，以問題“在本課中你們收獲了什么？”引發學生對本課知識內容的回顧，并交流探討自己的學習經驗與收獲，初步實現數學學習心得的交互。

其次，為學生提供若干個小木棒，鼓勵學生操作小木棒合作擺出不同的三角形。例如，直角三角形、銳角三角形、鈍角三角形和等腰三角形、等邊三角形等，并靈活運用所學探討不同三角形的內角和、三角形的各部分組成、三角形的特性，為其后續繪制“三角形”思維導圖做鋪墊。

最后，以微課呈現思維導圖的繪制方法與制作要點，并鼓勵學生基于自身對本課知識內容的理解認識展開導圖的繪制與制作（圖1）。

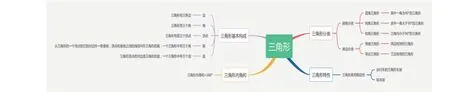
圖1 “三角形”思維導圖

學生不但在教師的循循善誘下完成了對“三角形”一課基礎知識的復習鞏固，其在繪制“三角形”一課思維導圖的過程中也意識與把握到了三角形各部分知識內容之間所存在的邏輯關系，數學基礎便就此而得到了有效夯實，其創新思維自然也會在扎實數學知識基礎的推動下而實現有機生長。［2］

二、創設開放情境，為創新思維的形成提供動力

在教學中培養與提升學生的創新思維，共需兩個基礎條件：一是豐富、完善的知識基礎；二是創新創造的熱情與動力。因此，教師在實際的教學過程中若想讓學生的創新思維實現持續發展、穩定提升，就要在夯實學生數學知識基礎的同時，基于對學生興趣偏好的認識把握，采取必要手段去調動與激發學生的創新創造興趣，以此來讓學生在興趣這一內驅力的驅動下展開自主創新、積極創造。［3］

例如，在引導學生探究人教版小學數學五年級上冊教材中《數學廣角——植樹問題》時，教師就可利用多媒體設備將這一探究性數學問題與學生的現實生活關聯起來，為學生創設開放、民主的探究性學習情境。

首先，利用多媒體設備為學生播放與展示學校美化校園環境、修繕花壇的視頻影像，并結合“如果學校想在一條20m 的小路上植樹，每間隔5m 栽一棵樹，你們有幾種植樹方案？”這一啟發性教學問題為學生創設“校園綠化，人人參與”的開放性數學教學情境，引發學生對問題的積極探討與創新思考。

其次，根據學生的學習水平與思維能力將學生劃分為若干個層次相當、水平相符的學習小組，讓學生以小組合作的形式對“植樹問題”展開各抒己見的開放性討論。在這一過程中，教師還可抓住教學時機向學生滲透數形結合與分類討論數學思想方法，鼓勵學生對不同的植樹情況進行分類討論，并利用數軸畫出不同情況下的植樹方案。

【方案一】在小路的一邊種樹

［情況1］路的兩端都要栽樹（圖2）：20÷5 ＋1 ＝5（棵）

圖2 兩端栽樹

［情況2］路的兩端都不栽樹（圖3）：20÷5－1 ＝3（棵）

圖3 兩端不栽樹

［情況3］路的一端栽樹，一端不栽樹（圖4）：20÷5 ＝4（棵）

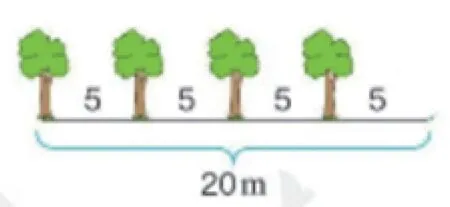
圖4 路的一端栽樹，一端不栽樹

【方案二】在小路的兩邊種樹

［情況1］路的兩端都要栽樹：（20÷5 ＋1）×2 ＝10（棵）

［情況2］路的兩端都不栽樹：（20÷5－1）×2 ＝6（棵）

［情況3］路的一端栽樹，一端不栽樹：20÷5×2 ＝8（棵）

最后，在學生利用數形結合與分類討論數學思想方法對“植樹問題”進行充分且深入探討分析后，教師就可組織各小組的代表在課堂中展示自己的小組學習成果，并與其他小組圍繞不同的植樹方案展開爭辯，從而在有效活躍學生數學學習思維，增強學生數學學習自信的同時，促使學生在開放、民主的學習情境中更好地感知到數學學科的魅力和積極思考的樂趣，進而生成濃厚且強烈的數學學習興趣，驅動自身創新思維的進一步發展。

在這一過程中，學生不但通過對數學思想方法的靈活運用得到了數學解題思路的開闊與問題解決能力的鍛煉，其在組內探討、組間交流的過程中也在潛移默化之中實現了思維的有效碰撞與潛力潛能的充分開發。這不僅加速了學生植樹方案的完善，同時也為其創新思維的發展提供了源源不斷的內驅力。

三、鼓勵大膽想象，為創新思維的發展創造條件

學生具有想象力豐富的年齡特點，而想象力恰恰便是學生發展創新思維的重要來源。［4］因此，教師在培養學生創新思維的過程中，就必須要尊重學生的這一天性，并要有意識地引導學生對數學知識、數學內容、數學問題展開有益聯想與大膽想象，以此來更好地推動學生的個性化發展與全面發展，為學生創新思維的提升創造優良條件。

例如，在教學人教版小學數學二年級下冊教材《100 以內的加法和減法（二）》一課后，教師就可在學生充分掌握100 以內整數的加法和減法計算方法后，為學生設置如下數學思考題：

小光的奶奶有六十元人民幣，她在一家超市花十元購買了一袋瓜子，那么收銀員應該找回小光奶奶多少錢？

該題與學生的生活實際有著密切聯系，不僅考驗著學生數學加減計算能力，同時也考查著小學二年級學生對人民幣的面值的認識。在思考與探究本題的解決方案的過程中，多數學生會受到定式思維的影響限制而用小光奶奶所有的60 元直接減去購買商品的10 元得出60－10 ＝50（元）的結論。對此，教師在引導學生進行釋疑時，便可向學生提出具有引導性的教學問題“在我們現實生活中，家長在購物后多會采用怎樣的支付方式付款？人民幣的面值大小共有幾種？”來引發學生對社會現實生活經驗的回憶，進而主動發散思維展開想象說出：“有現金支付、微信支付、支付寶支付與銀行卡支付四種支付方法；人民幣有硬幣與紙幣之分，硬幣有一角、五角、一元三種面值；紙幣有一元、五元、十元、二十元、五十元與一百元六種面值。”

待學生的想象力在問題的啟發下得到充分激活后，教師就可鼓勵學生從生活實際出發對上述問題展開討論。

【解答一】小光奶奶用現金支付

1．假設小光奶奶有十元紙幣與五十元紙幣，一袋瓜子的價格是十元，小光奶奶直接付給收銀員十元，不用找錢；

2．假設小光奶奶有三張二十元紙幣，一袋瓜子的價格是十元，小光奶奶付給收銀員二十元，收銀員需找回小光奶奶20－10 ＝10（元）；

3．假設小光奶奶為破整付給收銀員五十元，那么收銀員需找回50－40 ＝10（元）。

【解答二】小光奶奶用微信、支付寶、銀行卡線上支付

收銀員直接收取十元，不用找錢。

在教師有意識的引導與啟發下，學生不但對上述簡單的數學加減計算問題展開了大膽想象與積極聯想，而且在充分思考與深度探究的過程中也實現了思維定式的有效突破，認識到了數學知識的生活化本質特征。長此以往，學生的思維便會更加發散與靈活，其創新思維自然也會因學生思維與潛能的充分激活而得到有機發展。

四、尊重學生質疑，為創新思維的進階積蓄能量

質疑批判不僅是學生實現深度學習的必備條件，同樣也是提升學生創新思維，推動學生思維品質進階的重要方法。［5］學生的認知水平正處于具體運算階段，自我意識的持續增強也讓學生對客觀事物、生活現象存有強烈好奇心與探究欲。對此，教師在以提升學生創新思維為導向組織數學教學活動時，便可基于學生的這一認知發展特點鼓勵學生對數學結論、數學原理進行大膽質疑與積極批判，以此來讓學生在求異中實現創新，在探究中實現發展。

例如，在人教版小學三年級上冊《長方形與正方形》一課教學中，教師就可將長方形與正方形的周長計算公式直接出示給學生，并鼓勵學生對既有數學公式進行質疑與批判，以實際測量、實踐操作、合作探究等多種方式對長方形周長公式“C長方形=2×（長＋寬）”與正方形周長公式“C正方形=邊長×4”展開深入探討。學生不但能夠在質疑批判的過程中對長方形與正方形的周長計算公式形成更為深刻的印象，其創新思維與實踐能力也會因親歷“問題發現—問題提出—問題解決—問題分析”的釋疑過程而得到有效強化與穩定提升。

總而言之，學生正處于啟蒙開智的重要發展階段，在義務階段中，通過開發數學課程的育人功能與優勢對學生的創新思維能力進行針對性培養，不但有利于教學質量與效果的提升，對學生的成長與發展也大有裨益。因此，教師在實際的教學實踐過程中就必須要重視對數學學科思維品質培養價值的挖掘，并要緊密結合學生的認知發展規律采取有效手段對數學教學形式進行改革與優化，以此來讓學生的數學核心素養得到全面培養，促使學生通過學習數學學科知識實現茁壯成長、全面發展、持續發展。