生育率與經濟發展

喻勝華 趙盼

［摘 要］ 選取全球150個國家（或地區）的數據，采用兩種不同的分類方法，將樣本劃分為7個不同的子樣本，基于分位數回歸方法探究生育率與經濟發展之間的關系。實證結果表明，只有當經濟發展達到一定水平時，生育率與經濟發展之間才會出現反向“J”型關系，這種關系不僅與經濟發展水平相關，也與生育率水平相關。反向“J”型模式中的斜率雖然為正，但斜率較小。

［關鍵詞］ 生育率；經濟發展；反向“J”型關系；分位數回歸

［中圖分類號］ F063.4 ［文獻標識碼］ Ａ ［文章編號］ 1008—1763（2023）01—0058—08

Fertility Rate and Economic Development

——An Empirical Study Based on Quantile Regression

YU Sheng-hua， ZHAO Pan

（School of Economics and Trade， Hunan University， Changsha 410079， China）

Abstract：The data of 150 countries （or regions） in the world were selected， and the samples were divided into 7 different subsamples by two different classification methods. The relationship between fertility rate and economic development was explored based on the quantile regression method. The empirical results show that only when the economic development reaches a certain level， there will be a reverse “J-shaped” relationship between fertility rate and economic development， which is not only related to the level of economic development， but also to the level of fertility rate. In the reverse “J” pattern， the slope is positive but small.

Key words： fertility rate；economic development；reverse J-shaped relationship；quantile regression

一 引言及文獻綜述

在全球經濟取得空前增長的同時，人類的生育率卻經歷了大幅度的下降。根據世界銀行公開的數據，從1960年到1964年，世界總和生育率經過了短暫的小幅上漲之后持續下降，到2019年已降為2.403，但仍高于更替水平（2.1）。而反觀我國，在1960年，我國的總和生育率為5.756，此時，我國的總和生育率遠高于世界平均水平。從1960年到1965年，我國的總和生育率經歷了小幅上漲，之后迅速下滑，到1992年，我國的總和生育率已跌破更替水平，降至1.977。自1992年以來，我國的總和生育率一直處于更替水平之下。2013年，我國的“單獨二孩”政策正式開放，2016年，“全面二孩”政策開始正式實施。然而，近年來，我國的總和生育率并沒有隨生育政策的放松而顯著提升。經濟迅速發展的同時，伴之而來的似乎是總和生育率的持續下降。

學者們針對生育率與經濟發展之間的關系展開了廣泛的研究，其研究結論大致有如下四種：一是生育率與經濟發展之間存在負相關關系，該結論得到了學界的普遍認同。如Chen J等使用1990年和2000年的中國人口普查數據以及2005年的小型人口普查數據，分析了1975年至2005年間經濟發展和生育政策對廣東省生育率下降的影響，結果表明，經濟發展帶來了城市和農村居住、教育等方面的巨大變化，也極大地促進了廣東省生育率的下降^[1]。Kitaura K和Yakita A認為，在經濟增長過程中，每個孩子的教育成本會增加，生育率會下降^[2]。Zakaria M 等使用1972-2013年的面板數據，分析了孟加拉國、不丹、印度、馬爾代夫、尼泊爾、巴基斯坦和斯里蘭卡7個南亞國家的生育率，認為南亞地區的生育率隨經濟發展水平的提高而下降^[3]。Madsen J B等基于92個發展中國家1960-2014年間的數據，發現人均收入的增加是發展中國家生育率下降的重要決定因素之一^[4]。Gtmark F和Andersson M分析了歐洲東部、歐洲西部、阿拉伯國家等全球6個區域141個國家的相關數據，發現生育率與人均GDP呈負相關關系^[5]。二是生育率與經濟發展之間的負相關關系在不同的經濟發展階段存在異質性。比如，Furuoka F采用閾值回歸方法分別研究了總和生育率與人均GDP之間的關系以及生育率和人類發展指數之間的關系，研究表明，當收入水平低于閾值時，總和生育率與人均GDP之間存在顯著的負相關關系，當收入水平超過閾值時，總和生育率與人均GDP之間的負相關關系也不會逆轉為正相關關系。在人類發展指數較低的國家，生育率和人類發展指數之間存在強烈的負相關關系，在人類發展指數較高的國家，生育率和人類發展指數之間雖然也存在負相關關系，但這種負相關關系相對較弱^[6-7]。三是生育率與經濟發展之間存在正相關關系，該結論只是個別學者的觀點。如Brueckner M和Schwandt H基于1960-2007年間139個國家的面板數據，通過控制國家和時間固定效應，研究了人均GDP與人口增長率之間的關系，結果表明，人均GDP每增加1個百分點，各國的人口增長率就會增加約0.1個百分點^[8]。四是在不同經濟發展階段、不同地區，生育率與經濟發展之間存在完全相反的相關關系。Myrskyl? M等率先發現之前被學者們廣泛接受的總和生育率和人類發展指數之間的負相關關系發生了變化，即在人類發展指數處于低、中水平時，總和生育率隨著人類發展指數的增加而下降，當人類發展指數處于高水平時，進一步的發展可以扭轉總和生育率下降的趨勢，此時，總和生育率隨著發展水平的提高反而開始上升^[9]。該研究結論引發了學者們的熱烈討論：之前被廣泛接受的總和生育率與發展水平之間的負相關關系是否變成了反向“J”型關系？Dominiak P等使用1970-2011年間18個國家的面板數據分析了總和生育率與經濟增長之間的關系，認為總和生育率先隨著經濟增長而下降，而后會隨經濟增長而上升^[10]。Luci-Greulich A和Thévenon O研究了1960-2007年間OECD國家的經濟發展對生育率的影響，結果表明，總和生育率與經濟發展之間的強負相關關系不再成立，相反，當經濟發展到某一臨界水平時，這種強負相關關系會變成正相關關系^[11]。Ohinata A和Varvarigos D研究了人口轉型與經濟發展中的生育率反彈，認為當經濟發展到后期階段，經濟增長過程會產生足夠的資源，使每個家庭可以撫養更多的孩子，同時也能為每個孩子提供理想的教育投資，從而會出現生育率反彈^[12]。Fox J等通過調查1990-2012年間歐洲256個地區的數據發現，在許多地區內，生育率與經濟發展之間的負相關關系正在減弱，而在一些地區中可以觀察到負相關關系逆轉的趨勢^[13]。

現有研究多是對部分國家或部分地區的生育率與經濟發展之間的關系進行分析，鮮有從全球視角出發，對不同發展水平國家的總和生育率與經濟發展之間的關系進行深入探討；另一方面，從研究方法來看，現有研究多使用傳統的均值回歸方法及其相關的最小二乘估計，該方法所能反映的信息量往往是相對有限和狹隘的，且其假設條件在實際應用中經常無法滿足。為此，本文主要做了如下工作：一方面，試圖從全球視角出發，選取了全球150個國家（或地區）的數據，并使用更深入、更詳細、更均勻的分類方式，將150個國家（或地區）的相關數據分為7個子樣本，在此基礎上研究生育率與經濟發展之間的關系；另一方面，在基準回歸模型的基礎上，引入了分位數回歸模型，探索生育率與經濟發展之間是否存在反向“J”型關系。如果二者之間存在反向“J”型關系，則進一步探索二者之間的反向“J”型關系是否與生育率水平相關。

二 機理分析

（一）生育率和經濟發展負相關的經濟學解釋

Becker G S和Barro R J提出了一種分析生育率的理論框架^[14-15]，該理論框架被稱為“新家庭經濟學理論”，它為解釋生育率和經濟發展之間存在負相關關系提供了主要的理論依據。該理論將孩子視為一種正常品，認為生育需求的收入效應和替代效應的權衡決定了生育率的高低。隨著經濟的發展，女性的收入增加，進而會促使更多女性參與勞動。在不能將工作和養育孩子平衡時，如果待在家里照顧孩子，則意味著女性工資的損失，這種損失是女性生育孩子的間接成本。因此，女性就業和生育率之間為替代效應。基于該理論，Sprague A認為，女性勞動參與度的提高以及女性工資的提升使得生育的影子價格提升，從而導致了生育率的下降^[16]。

Becker G S等基于新家庭經濟學理論，從孩子數量和質量之間相互作用的角度解釋了生育率的下降。他們研究了在家庭收入不變的約束下，在孩子數量和孩子質量之間進行權衡，以實現家庭效用函數的最大化^[17]。在現代社會中，隨著經濟的發展，為了應對新的經濟現實和社會需求，父母會更注重提高孩子的質量。對于父母而言，孩子質量的提高需要付出更多的成本，所以會傾向于減少孩子的數量，進而導致了生育率的下降。

（二）生育率和經濟發展負相關關系逆轉的理論分析

生育率與經濟發展之間的關系在理論和實證上仍是不明確的，雖然它們之間的負相關關系被多數學者所接受，但也受到了一些學者的質疑，認為二者之間的負相關關系并不總是會保持，而是可能會發生逆轉，甚至會表現為正相關關系。

根據新家庭經濟學理論，在家庭中，當女性不得不在參加工作和撫養孩子之間做出選擇時，才會導致生育率下降。但是，如果女性能進入工作崗位，同時也能兼顧撫養孩子，隨著經濟的發展，女性的工資也會隨之增加，高工資使之更容易負擔撫養孩子的成本，此時女性的工資不僅僅為替代效應，其收入效應可能開始占主導地位，經濟發展和女性就業對生育率的負向影響可能會減弱^[18]。

最近幾年，在一些發達國家中，偏向技能的技術變革增加了技能溢價，因此降低了兒童保育服務的相對價格，而女性平均工資的增加使育兒成本變得更容易承受。因此，經濟發展和女性工資對生育率的影響可能會由負向逆轉為正向^[19]。Luci-Greulich A和Thévenon O進一步指出，在一些高度發達的國家，如果能提高女性就業和生育的兼容性，則經濟發展和生育率之間的負相關關系會出現逆轉，表現為反向“J”型關系。但如果經濟發展過程中，沒有相應的制度變革，以提高父母把工作和家庭生活結合起來的可能性，那么生育率增長的可能性將很小^[11]。

近幾十年來，不少發達國家實施了不盡相同的家庭政策，雖然各國實施的家庭政策不盡相同，但鼓勵生育是其中的一個重要目標。很多政策均有助于降低家庭撫養孩子的機會成本，也有助于兒童保育。比如，家庭政策中的育兒假計劃可以保證父母在休假一段時間后返回到以前的工作崗位，減少了未來職業選擇的不確定性；家庭政策中，公共兒童保育服務的改善可以解決父母忙于工作而無法撫養孩子的后顧之憂，提高父母工作和生育的兼容性，從而降低了父母生育孩子的機會成本。還有一些家庭政策會給予育兒補貼或減免稅收等。這些家庭政策均不同程度地降低了家庭生育孩子的機會成本，有助于削弱生育率和經濟發展之間的負相關關系，甚至有可能將兩者之間的負相關關系扭轉為正相關。

互聯網技術的飛速發展為人們創造了比之前更靈活的工作安排，在這種情況下，員工不需要在所有工作時間都在正常工作場所出現。隨著經濟的發展，技術進步正改變著21世紀經濟活動的空間組織。在此過程中，相對靈活的工作安排可以將撫養孩子和工作相結合，這對家庭的生育決定產生了積極的影響，有助于逆轉經濟發展與生育率之間的負相關關系^[20]。除經濟因素外，也有學者從移民等其他角度解釋了生育率逆轉。

三 研究設計

（一）樣本分類方法

總和生育率（TFR）反映了女性一生中生育孩子的總數，是最重要的人口指標之一。本文使用總和生育率作為生育率的指標，其數據來源于世界銀行公開數據。經濟發展用人均GDP（GDPpc）來衡量，其數據來自賓夕法尼亞大學世界表（Penn World Table，PWT）。鑒于有些國家（或地區）某些年份的數據不完整，我們選取了全球150個國家（或地區）1970-2010年的數據。

本文根據2010年各國人均國民收入，將150個國家（或地區）分為高收入國家、中上收入國家、中下收入國家、低收入國家4個子樣本，然后分別研究這4個子樣本中不同國家的總和生育率與經濟發展之間是否存在反向“J”型關系。此外，將樣本按照人均GDP的不同均等地分為低、中、高3個子樣本，分別用GDPpc-low、GDPpc-middle、GDPpc-high表示。值得注意的是，在該分類中，同一個國家在不同時期可能屬于不同的子樣本。以我國為例，1970年，我國的人均GDP是361美元，屬于GDPpc-low這一子樣本，然而，2010年我國的人均GDP達到了4628美元，屬于GDPpc-middle這一子樣本。

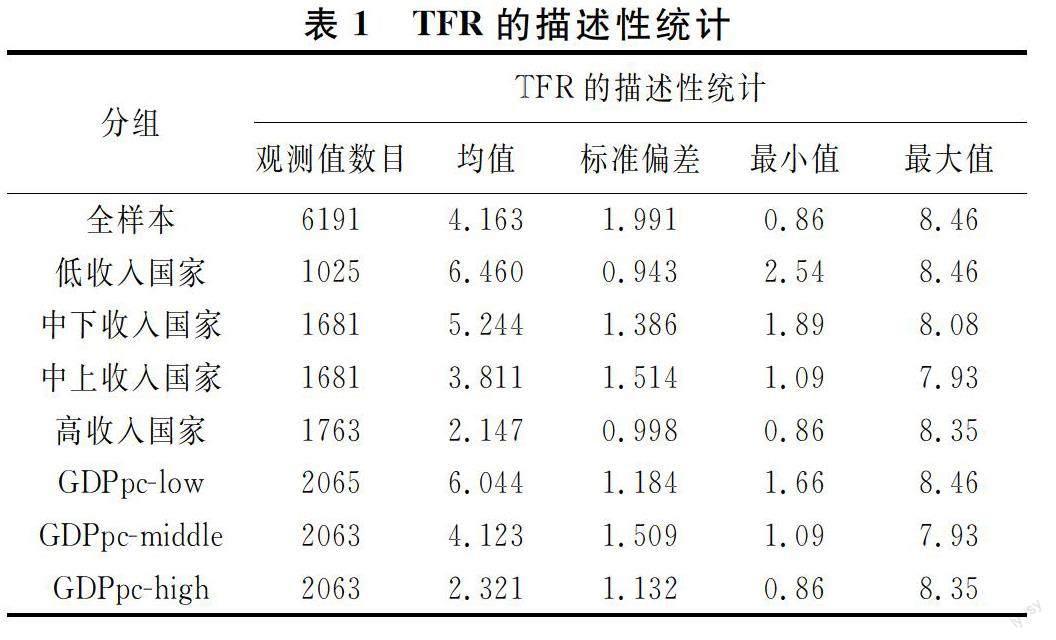
（二）變量的描述性統計

表1和表2分別報告了全樣本和7個子樣本的描述性統計結果。

（三）模型設置

由于數據中GDPpc和TFR差距很大，所以，模型中對GDPpc取自然對數。本文使用如下基準回歸模型：

其中，αi表示不隨時間而變化的個體特征，β0是常數項，ut表示時間效應，εit表示隨機誤差項。

模型（1）中包含了二次項，如果二次項的系數估計值顯著為正，而一次項的系數估計值顯著為負，則可以初步認為總和生育率與人均GDP之間的關系在人均GDP達到閾值前是負相關關系，超過該閾值后，它們之間的關系會發生逆轉，變為正相關關系，即總和生育率和經濟發展之間存在反向“J”型關系。

為了更深入地探索總和生育率與人均GDP之間的反向“J”型關系是否與生育率水平相關，除了使用基準回歸模型（1）外，也在基準回歸模型（1）的基礎上，引入了線性分位數回歸模型，如式（2）所示：

其中，QTFRitτln GDPpcit表示總和生育率的條件分位數，模型（2）中的系數會隨著分位數τ的不同而發生變化，即為τ的函數。

（四）模型估計方法

首先，針對基準回歸模型（1）使用最小二乘法，分別研究全樣本以及高收入國家、中上收入國家、中下收入國家、低收入國家、GDPpc-low、GDPpc-middle、GDPpc-high 7個子樣本，探討總和生育率和經濟發展之間是否存在反向“J”型關系。

與最小二乘法不同，分位數回歸可以通過被解釋變量的不同分位數對解釋變量進行回歸，從而得到被解釋變量不同分位數下的回歸結果。分位數回歸可以提供多條不同的回歸曲線，從而對被解釋變量在整體分布上的回歸做出更清楚的闡釋，挖掘的信息量也更加豐富。分位數回歸對于變量間的統計關系能描述得更詳細、更全面。為此，除了使用基準回歸模型外，本文也針對線性分位數回歸模型（2），使用分位數回歸技術，以進一步探討生育率和經濟發展之間的反向“J”型關系以及反向“J”型關系是否與生育率水平相關。

四 實證結果與分析

（一）基準回歸結果與分析

表3給出了基準回歸模型（1）的最小二乘回歸結果。

由表3易知，對于低收入國家、中下收入國家、中上收入國家、GDPpc-low、GDPpc-middle這5個子樣本而言，總和生育率和經濟發展之間不存在反向“J”型關系。

對于全樣本以及高收入國家和GDPpc-high這2個子樣本而言，lnGDPpcit的系數β1的估計值是負的，且在0.01水平下顯著。同時，其二次項系數β2的估計值是正的，且在0.01水平下顯著，可初步認為，總和生育率和經濟發展之間的負相關關系發生了逆轉。

為了更準確地判斷總和生育率和經濟發展之間的關系，我們不僅使用模型（1）的系數β1和β2的估計值，同時也考慮變量的邊際效應，即

邊際效應的下界、上界及閾值如表4所示。其中，下界和上界是分別根據lnGDPpcit的最小值和最大值計算得到的，而閾值則通過令式（3）的右邊等于零計算得到。

由表4易知，對于全樣本以及高收入國家和GDPpc-high這2個子樣本而言，下界處的邊際效應分別為-2.006、-1.376、-0.626，這表明在下界處，總和生育率和經濟發展之間存在負相關關系，而上界處的邊際效應分別為2.009、2.127、3.365，此時，總和生育率和經濟發展之間存在正相關關系。從下界到閾值，總和生育率和經濟發展之間是負相關關系，而當GDPpc超過閾值后，它們之間的關系發生了逆轉，二者之間的關系轉變為正相關關系。可以認為，在全樣本以及高收入國家和GDPpc-high這2個子樣本中，總和生育率與經濟發展之間存在反向“J”型關系。高收入國家和GDPpc-high這2個子樣本中TFR和GDPpc的散點圖及擬合線分別如圖1和圖2（太陽花散點圖）所示。圖中的1個小圓圈代表1個觀測值，1朵太陽花代表多個觀測值，擬合線是使用局部加權回歸散點平滑法得到的。

在圖1中，1朵淺色太陽花的每片花瓣代表1個觀測值，1朵深色太陽花的每片花瓣代表4個觀測值。在圖2中，1朵淺色太陽花的每片花瓣代表1個觀測值，1朵深色太陽花的每片花瓣代表5個觀測值。

根據表3的基準回歸結果，并結合表4邊際效應的下界、上界以及閾值，可以認為在高收入國家和GDPpc-high這2個子樣本中，總和生育率和經濟發展之間存在反向“J”型關系，圖1和圖2進一步證實了這一點。此外，在圖1和圖2中，絕大多數的淺

色太陽花和深色太陽花分布在反向“J”型圖案負斜率的部分，而僅有少部分的小圓圈分布在反向“J”型圖案正斜率的部分。也就是說，對于多數觀測值而言，TFR和GDPpc之間存在負相關關系，僅有少部分觀測值的TFR是隨著GDPpc的增加而增加。另一方面，在斜率為正的部分，擬合線傾斜程度較小。這說明，雖然TFR是隨著GDPpc的增加而增加，但增加的幅度較小。

（二）分位數回歸結果與分析

前面的結論表明，當人均國民收入達到高收入水平或者當人均GDP較高時，總和生育率與經濟發展之間的關系才會發生逆轉，即二者之間的反向“J”型關系與經濟發展水平相關。為此，我們進一步探討總和生育率與經濟發展之間的反向“J”型關系是否與生育率水平相關。

當被解釋變量的分布函數是非正態分布時，最小二乘估計不再是一個好的估計。此時，分位數回歸技術是一種很好的替代方法，它可以提供一種更穩健的估計。首先對高收入國家和GDPpc-high這2個子樣本的總和生育率進行正態性檢驗，表5給出了相應的檢驗結果。

由表5可知，高收入國家和GDPpc-high這2個子樣本的總和生育率均不服從正態分布。為此，我們針對這2個子樣本以及線性分位數回歸模型（2），進一步探討總和生育率與經濟發展之間存在的反向“J”型關系以及其反向“J”型關系是否與生育率水平相關。

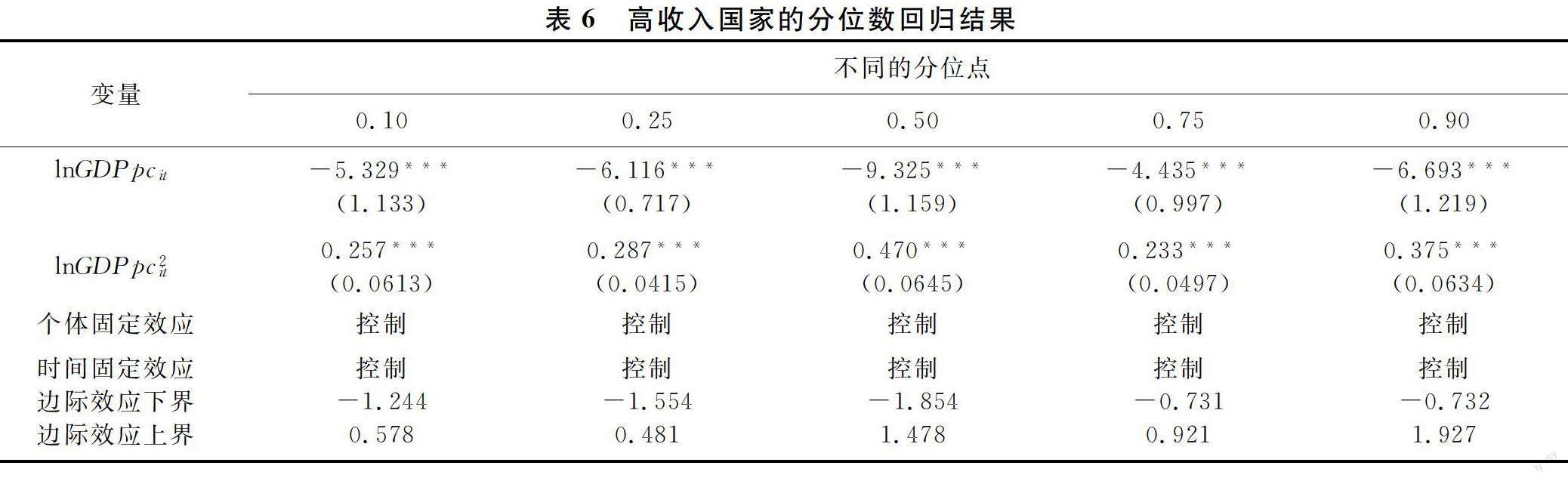
表6和表7分別給出了針對高收入國家和GDPpc-high這2個子樣本的分位數回歸結果。其中，0.10表示低分位數，0.25表示中低分位數，0.50表示中分位數，0.75表示中高分位數，0.90表示高分位數。除了給出分位數回歸結果外，表6和表7還給出了邊際效應的下界和上界。

表6和表7中分位數回歸結果括號內的數字為采用MCMC方法得到的估計標準誤。“*”“^**”和“^***”分別表示對應系數在0.1、0.05、0.01水平上顯著。

由表6和表7可知，對高收入國家和GDPpc-high這2個子樣本而言，在5個分位數處，邊際效應的下界均為負值，這意味著，此時總和生育率與經濟發展之間存在負相關關系。而邊際效應的上界在5個分位數處的值都為正，這意味著，此時總和生育率與經濟發展之間的負相關關系已經發生了逆轉，轉變為正相關關系，即總和生育率與經濟發展之間存在反向“J”型關系，這與基準回歸的結果是一致的。此外，lnGDPpcit和lnGDPpc2it 在5個分位點處的回歸系數的估計值各不相同，這表明在不同的分位點處，總和生育率和經濟發展之間的反向“J”型關系是不同的。

表6和表7中的0.10和0.25分別表示低生育水平的國家和較低生育水平的國家，而0.75和0.90分別表示較高生育水平的國家和高生育水平的國家。為了更準確地檢驗不同生育水平下的反向“J”型關系是否顯著不同，表8給出了高收入國家和GDPpc-high這2個子樣本的分位數回歸系數顯著性差異的Wald檢驗。

由表8易知，與生育水平相對較低的國家（0.10和0.25）相比，在生育水平較高的國家（0.90和0.75）中，經濟發展對總和生育率的影響是顯著不同的。也就是說，在不同的生育水平下，總和生育率和經濟發展之間的反向“J”型關系是顯著不同的。進一步可以看出，反向“J”型關系的負斜率和正斜率均隨生育率的不同而不同。對正斜率而言，GDPpc的增加，將導致TFR增加的量隨生育率的不同而不同。對負斜率而言，GDPpc的增加，將導致TFR減少的量隨生育率的不同而不同。這表明，除了GDPpc外還有其他因素影響總和生育率，這些因素中可能包括家庭政策、女性就業等。

在高收入國家和GDPpc-high這2個子樣本中，生育率與經濟發展之間存在反向“J”型關系，這可能是因為在這些發達的國家（或地區），偏向技能的技術變革增加了技能溢價，從而降低了兒童保育服務的相對價格。也可能是因為這些發達的國家實施了鼓勵生育的家庭政策，從而降低了父母生育孩子的機會成本。此外，在不同生育水平的國家，經濟發展與總和生育率之間的反向“J”型關系是不同的。也就是說，生育率與經濟發展之間的反向“J”型關系不僅取決于經濟發展水平，也與生育率有關。這可能是因為不同的發達國家其生育率不同，實施的家庭政策也不盡相同等。

五 政策建議

自改革開放以來，我國經濟取得了快速的發展，到2021年，人均GDP已接近世界平均水平。在經濟快速發展的同時，我國的總和生育率卻經歷了大幅度下降。甚至有專家認為，我國已經掉入了“低生育率陷阱”。我國第七次人口普查的數據顯示，我國的總和生育率已跌至1.3，已經低于國際上通常認為的 “高度敏感警戒線”。在世界范圍內，總和生育率低于1.3的國家（或地區）僅有韓國，新加坡，中國的香港、澳門等少數幾個國家（或地區）。基于前面的實證分析結果，就如何改變當前我國生育率極低的現狀提出如下政策建議：

首先，實證分析結果表明，在高收入國家和GDPpc-high這2個子樣本中，生育率與經濟發展之間存在反向“J”型關系。而在低收入國家、中下收入國家、中上收入國家、GDPpc-low、GDPpc-middle這5個子樣本中，沒有觀測到總和生育率與經濟發展之間存在反向“J”型關系。也就是說，只有當經濟發展到一定階段后，總和生育率才有可能回升。所以，我國應該通過技術創新和產業升級等，尋求新的經濟增長點，進而提高經濟發展水平。

其次，建議借鑒國外的經驗，并結合目前我國的國情，出臺有助于提高我國生育率的家庭政策。例如，降低住房價格、養育孩子的成本、教育的費用等，進而緩解年輕人生育孩子的壓力。

再次，需要意識到的是，雖然在高收入國家和GDPpc-high這2個子樣本中，總和生育率與經濟發展之間存在反向“J”型關系，但圖1和圖2進一步表明：對多數觀測值而言，TFR和GDPpc之間存在負相關關系，僅有少部分觀測值的TFR是隨著GDPpc的增加而增加。另外，斜率為正的部分，擬合線傾斜程度較小。也就是說，雖然TFR隨著GDPpc的增加而增加，但增加幅度較小。盡管很多發達國家為了逆轉TFR，采取了不盡相同的政策，但TFR增加的幅度依舊不大。這意味著，對現階段生育率極低的我國而言，只有最大限度地實施“鼓勵生育”的政策，才有可能使我國的生育率緩慢回升。

［參 考 文 獻］

［1］

Chen J， Retherford R D， Choe M K， et al. Effects of population policy and economic reform on the trend in fertility in Guangdong province， China， 1975–2005[J]. Population Studies， 2010（1）： 43-60.

［2］ Kitaura K， Yakita A. School education， learning by doing， and fertility in economic development[J]. Review of Development Economics， 2010（4）： 736-749.

［3］ Zakaria M， Fida B A， Janjua S Y， et al. Fertility and financial development in South Asia[J]. Social Indicators Research， 2017（2）： 645-668.

［4］ Madsen J B， Moslehi S， Wang C. What has driven the great fertility decline in developing countries since 1960？[J]. The Journal of Development Studies， 2018（4）： 738-757.

［5］ Gtmark F， Andersson M. Human fertility in relation to education， economy， religion， contraception， and family planning programs[J]. BMC Public Health， 2020（1）： 1-17

［6］ Furuoka F. Total fertility rate and per capita income： new empirical findings from France[J]. Actual Problems of Economics， 2012 （3）： 469-479.

［7］ Furuoka F. Is there a reversal in fertility decline？ An economic analysis of the “fertility J-curve”[J]. Transformations in Business and Economics， 2013（2）：44-57.

［8］ Brueckner M， Schwandt H. Income and population growth[J]. The Economic Journal， 2015（589）： 1653-1676.

［9］ Myrskyl? M， Kohler H P， Billari F C. Advances in development reverse fertility declines[J]. Nature， 2009（7256）：741-743.

［10］Dominiak P， Lechman E， Okonowicz A. Fertility rebound and economic growth： New evidence for 18 countries over the period 1970-2011[J]. Equilibrium-Quarterly Journal of Economics and Economic Policy， 2015（1）： 91-112.

［11］Luci-Greulich A， Thévenon O. Does economic advancement ‘cause a re-increase in fertility？ An empirical analysis for OECD countries （1960–2007）[J]. European Journal of Population， 2014（2）： 187-221.

［12］Ohinata A， Varvarigos D. Demographic transition and fertility rebound in economic development[J]. The Scandinavian Journal of Economics， 2020（4）： 1640-1670.

［13］Fox J， Klüsener S， Myrskyl? M. Is a positive relationship between fertility and economic development emerging at the sub-national regional level？ Theoretical considerations and evidence from Europe[J]. European Journal of Population， 2019（3）： 487-518.

［14］Becker G S， Barro R J. A reformulation of the economic theory of fertility[J]. The Quarterly Journal of Economics， 1988（1）： 1-25.

［15］Barro R J， Becker G S. Fertility choice in a model of economic growth[J]. Econometrica， 1989（2）： 481-501.

［16］Sprague A. Post-war fertility and female labour force participation rates[J]. The Economic Journal， 1988（392）：682-700.

［17］Becker G S， Lewis H G. On the interaction between the quantity and quality of children[J]. Journal of Political Economy， 1973（2）： 279-288.

［18］Day C. The dynamics of fertility and growth： Baby boom， bust and bounce-back[J]. The B.E. Journal of Macroeconomics， 2004（1）： 114-132.

［19］Martínez D F， Iza A. Skill premium effects on fertility and female labor force supply[J]. Journal of Population Economics， 2004（1）： 1-16.

［20］Begall K， Mills M. The impact of subjective work control， job strain and work–family conflict on fertility intentions： A European comparison[J]. European Journal of Population， 2011（4）： 433-456.