基于特征諧波的地鐵直流饋線保護方法

蘇 煜,湯士明,張子揚

(1.合肥軌道交通集團有限公司,安徽 合肥 230000;2.南京南瑞繼保電氣有限公司,江蘇 南京 210000;3.天津大學智能電網教育部重點實驗室,天津 300072)

0 引言

地鐵作為公共交通的重要組成部分,因高效、快捷、載客量大等優點成為了緩解城市交通的有效工具。直流牽引供電系統的安全運行是地鐵運行的重要保障,一旦直流牽引供電系統中的饋線發生故障,不僅造成地鐵停運而且威脅人身以及設備安全。因此,研究地鐵直流饋線的保護新原理具有重要價值。

常規的地鐵直流饋線保護主要包括:大電流脫扣保護、電流上升率及電流增量保護、定時限過流保護、框架保護等[1]。大電流脫扣保護[2]是開關自帶的保護,反應饋線出口近端發生的嚴重短路,在短路電流還未達到峰值以前即可切除故障,其迅速跳閘功能可避免故障對饋線及設備造成更大損害。電流上升率及電流增量保護[3]分瞬時動作段和延時動作段,既滿足了在饋線出口近端至中點之間發生故障的快速切除,也可實現遠端故障時延時跳閘的功能。定時限過流保護[4]持續監測電流幅值,當電流幅值大于整定值的時間超過整定延時時動作,因其延時較長不能迅速切除故障而常作為電流上升率及電流增量保護的后備保護,用于切除饋線遠端故障。框架保護[5]主要反應絕緣損壞等情況下直流設備正極對地產生的接地電流增大而動作,起到對人身以及設備安全的保護作用。

近幾年針對直流饋線保護,學者們也提出了一些新的保護原理。文獻[6]提出一種基于Mexh小波變換的城市軌道交通直流饋線保護方案,通過使用Mexh小波變換提取時間常數變化特征來區分饋線遠端故障和機車恒轉矩運行狀態,解決了機車恒轉矩狀態下電流上升率大可能引起保護誤動作的問題,該方案缺點是小波變換需要時間,影響保護動作的快速性。文獻[7]提出一種地鐵直流饋線電流上升率及電流增量保護的改進方法,該方法針對傳統電流上升率及電流增量保護難以區分低頻振蕩信號的問題,指出可以利用多尺度能量分析法識別并剔除低頻振蕩信號,避免了保護誤動作。

本文提出一種基于24次特征諧波電流幅值的地鐵直流饋線保護方法,依據故障后特征諧波電流增大的原理識別故障,MATLAB/Simulink仿真證明了該方法的有效性。該方法針對故障前有無車輛行駛設置了不同的保護判據,與傳統保護相比有效避免在升弓和過分段絕緣情況下誤動作。

1 直流饋線故障前后24次特征諧波的變化規律

1.1 24次諧波產生原因

24脈波整流能有效減小直流牽引網上的諧波,并減小了整流器工作對交流電網的干擾,因此在地鐵牽引系統中得到廣泛使用[8]。24脈波整流系統接線示意見圖1,其由2 臺網側分別移相±7.5°的等容量整流變壓器以及4組三相整流橋并聯組成,其中,網側移相+7.5°的變壓器連接組別為Dy11d0,網側移相-7.5°的變壓器連接組別為Dy1d2[9]。為了使網側電壓移相7.5°,整流變壓器網側采用了延邊三角形接法。整流變壓器的延邊三角形接線以及對應的相量見圖2,可見電源電壓UAB、UBC和UCA分別滯后網側繞組的輸出電壓UA0B、UB0C和UC0A一個角度,該角度被稱為延邊三角形接法變壓器的移相角,滯后為負、超前為正。只要調整好延邊匝數占繞組總匝數的比例即能保證UAB、UBC和UCA移相-7.5°。

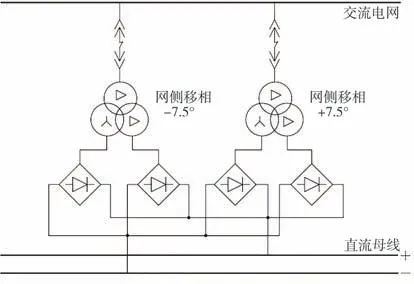
圖1 24脈波整流系統接線示意

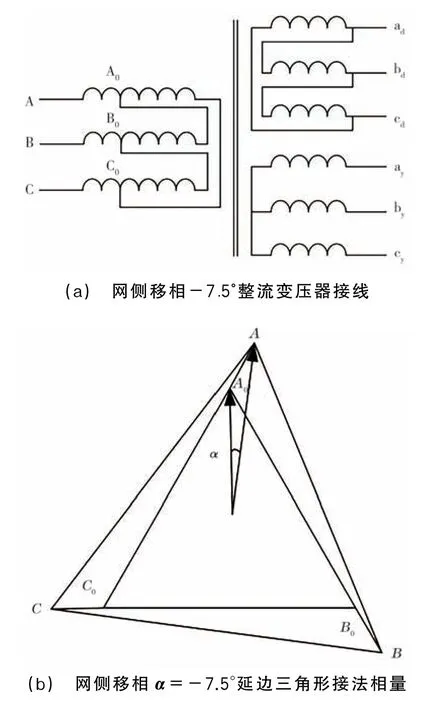
圖2 整流變壓器接線及相量

由整流變壓器的接線方式分析得到其閥側線電壓相量見圖3。圖中電壓下角標x ij表示整流變壓器的閥側端子,其中:x=a,b,c表示三相端子;i=1,2表示變壓器編號,網側移相+7.5°的整流變壓器編號為1,網側移相-7.5°的整流變壓器編號為2;j=y或d,表示閥側繞組連接方式。因此,a1y和b1y分別表示網側移相+7.5°的整流變壓器閥側星接繞組的a相和b相端子;ua1yb1y則表示端子a1y和b1y間的電壓,圖3中其他線電壓同理。

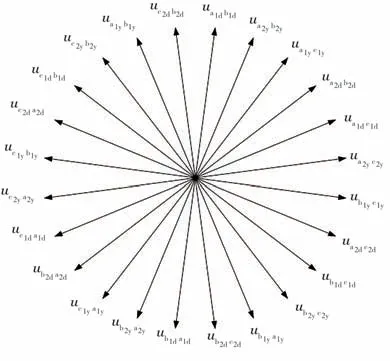
圖3 整流變壓器閥側線電壓相量

由圖3可以看出,整流變壓器閥側24個線電壓相量(ua1yb1y,uc2db2d,…)均與其相鄰的兩線電壓相量之間互差15°。閥側線電壓經4組三相整流橋整流后并聯,構成輸出24脈波直流的直流電源。

24脈波整流輸出電壓在其一個周期內的表達式為

式中:Udm為整流變壓器輸出線電壓的峰值;m∈Z;ω=2πf0為工頻角頻率。

對24脈波整流輸出電壓u d在全時域上進行傅里葉變換,得到傅里葉系數項a0,a n和b n

式中:n=24k;k=1,2,…;T為24脈波整流輸出電壓的周期,T=1/24f0。

因此,ud可以用傅里葉級數的形式表達為

其中的24次諧波電壓為

由式(5)可以看出:24脈波整流輸出電壓的主成分為直流分量,還包含24k次諧波分量。諧波中,24次諧波幅值最大,隨著k的增大,對應的諧波幅值越來越小。24k次電壓諧波分量將在直流牽引網上產生24k次諧波電流,由于24次諧波幅值最大,故障后增大最明顯,因此本文中將24次諧波作為特征諧波。

1.2 故障前后24次特征諧波電流幅值的變化規律

地鐵直流牽引網的供電回路主要由接觸網以及鋼軌構成。接觸網可分為架空式和接觸軌式,其中剛性架空式接觸網由匯流排和接觸線組成,下文以此種接觸網為例進行分析。隨著電流頻率的升高,趨膚效應會愈加顯著,本文在分析24次諧波電流時考慮了趨膚效應的影響。

導體的電感分為磁場在導體內部形成的內電感和磁場在導體外部形成的外電感2部分,其中,內電感與導體內部的電流分布相關,而導體在趨膚效應的作用下電流趨向于在表面流動,因此導體截面周長對其內電感數值的影響較大。在頻率較高時,通常使用等周長圓柱截面代替不規則導體截面計算內阻抗[10],因此本文計算匯流排、接觸線和鋼軌的內阻抗時,將3者均等效為等周長半徑的實心圓柱體。

使用文獻[11]中給出的近似計算方法,根據匯流排(PAC110)、接觸線(CTHA- 120)和鋼軌(P60)的參數,可以計算得到考慮趨膚效應時地鐵24次諧波流通路徑的內阻抗,見表1。其中剛性懸掛的參數為匯流排和接觸線并聯后的結果,鋼軌的參數為2條鋼軌并聯后的結果。

表1 24次諧波內阻抗 Ω/km

導體的外電感與導體的位置以及周圍環境有關,采用剛性架空式接觸網的地鐵供電回路其值為0.78 m H/km[12]。

由于24次諧波頻率較高,因此地鐵供電回路的外電抗值遠大于內阻抗,故在后續原理分析中忽略電阻以及剛性懸掛的內電感,僅保留外電感以及鋼軌內電感。

正常運行時,直流牽引系統的電路如圖4所示。圖4中LT表示整流變壓器以及交流系統的等值電感,Le表示牽引網的外電感,Lr表示鋼軌電感,Ls表示地鐵車輛上裝設的濾波電感,C表示地鐵車輛上裝設的支撐電容,R表示負載,n由地鐵車輛的編組方式決定,VD1-VD6組成4組三相整流橋中的1組。24次諧波的流通路徑如圖4中箭頭所示。因為支撐電容C對高頻分量具有濾除作用,所以流過直流接觸網和負荷的電流主要是直流電流,而數值較小的諧波分量通過支撐電容C流回系統。

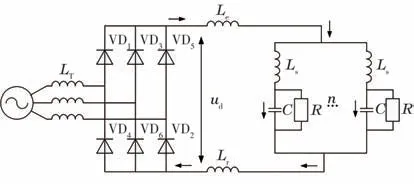
圖4 正常運行時的電路

由于24次諧波頻率較高,對其起阻礙作用的主要為牽引網外電感Le、鋼軌電感Lr以及濾波電感Ls,因此忽略支撐電容C以及負載R,并令n=6,可以得到簡化后的24次諧波電流流通路徑如圖5所示,ud24表示24次諧波電壓源,Lss=Ls/6表示地鐵車輛電感。

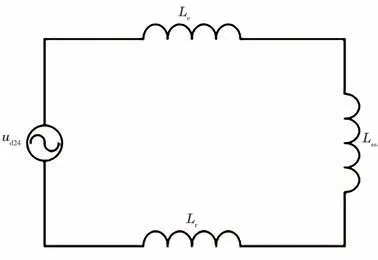
圖5 正常運行時的簡化電路

根據圖5寫出24次諧波電流流通路徑上的阻抗為

當直流接觸網上發生短路后,故障附加網絡見圖6,-u′為24次諧波電壓源,其數值上等于故障點正常運行電壓的負值;i24f為24次諧波電流的故障分量;Le1和Lr1表示整流橋出口至短路點的牽引網外電感和鋼軌電感,Le2和Lr2表示短路點至地鐵車輛之間的牽引網外電感和鋼軌電感,則Le=Le1+Le2,Lr=Lr1+Lr2。

圖6 故障分量電路

由圖6得出24次諧波電壓源為

式中:ud24由式(6)給出。因此,24 次諧波電流的故障分量為

根據疊加原理,故障后測得直流饋線上的24次諧波電流為

其幅值為

式(12)與式(8)比較可見,故障發生后測得的直流饋線24次諧波電流的幅值明顯增大。根據這一特性即可設計基于24次特征諧波的地鐵直流饋線保護方法。

2 基于24次特征諧波電流幅值的地鐵直流饋線保護方法

本文提出的保護方法采用直流電流變化率大于定值作為啟動判據。啟動判據如下

式中:ΔI Z是啟動判據的整定值。

保護啟動后,依據故障后24次特征諧波電流幅值增大的特征反應饋線故障,具體判據如下

式中:判據①用于故障前本段牽引網上無車輛行駛情況;判據②用于有車輛行駛情況,判據滿足則判定為直流饋線發生故障;I t+ΔtP為故障后延時ΔtP的24次諧波電流幅值;ΔtP按照躲過升弓、過分段絕緣的時間來取值;I ZN和I Zmax為整定值。

判定有無車輛行駛的判據如下

該保護整定值的選取原則如下。

對于啟動判據,取其整定值ΔI Z=KSID/ms,ID為本段牽引網正常運行時的直流電流值;可靠系數KS=0.05~0.1。

對于保護判據,令I24min和I24max分別為地鐵車輛在本段牽引網上正常運行時的24次諧波電流最小幅值和最大幅值,可以在實際運行中測量得到;I24為故障前的24次諧波電流幅值,則保護判據中的整定值按照如下原則整定

式中:K1、K2和K3為可靠系數,取值為K1=0.6~0.8,K2=1.1~1.2,K3=1.1~1.2。

保護方法的流程如圖7所示,具體實現步驟如下。

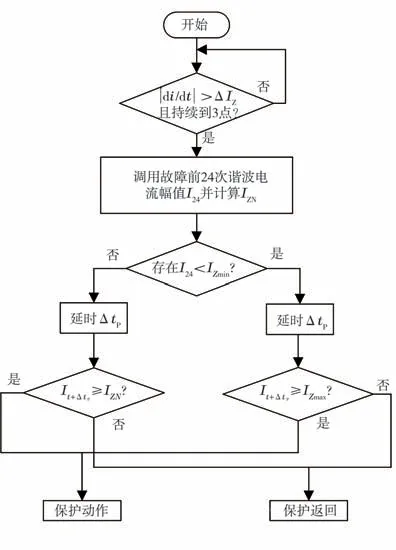
圖7 保護方法流程

1)若啟動判據動作,將電流變化率|di/dt|大于整定值的第1個點作為故障起始點;

2)調用故障前全波傅里葉算法求得的24次諧波電流幅值I24。

為避免地鐵車輛在升弓以及過分段絕緣時引起電流突變而導致保護誤動作,需根據I24的大小判斷故障前是否有地鐵車輛行駛。

若滿足

則判故障前本段牽引網上無地鐵車輛行駛。

若滿足

則判故障前本段牽引網上有地鐵車輛行駛。

3)使用全波傅里葉算法計算故障后延時ΔtP的24次諧波電流幅值I t+ΔtP。

故障前牽引網上無地鐵車輛行駛,則利用式(14)的保護判據①判斷直流饋線上是否有故障發生;故障前牽引網上有地鐵車輛行駛,則利用式(14)的保護判據②判斷直流饋線上是否有故障發生。

3 仿真分析

3.1 仿真模型

在MATLAB/Simulink中建立如圖8所示的地鐵牽引系統仿真模型。主變壓器、整流變壓器以及整流橋參數參照文獻[13]設置。地鐵車輛模型內部結構與圖4中地鐵車輛電路一致,濾波電感Ls=8 m H,支撐電容C=4 m F[14],負載R的大小根據地鐵列車的取流情況調整。考慮趨膚效應對接觸網和鋼軌24次諧波阻抗的影響,采用圖9的線路等效方式。其中,Le為牽引網外電感;取Rline=0.013 5Ω/km,Rr=0.013 7Ω/km 為接觸網和鋼軌的直流電阻[12-13];R1、R2以及L1、L2則通過計算得到,使得Rline、R1和L1以及Rr、R2和L2組成的串并聯電路的阻抗分別等于表1中剛性懸掛和鋼軌的內阻抗。牽引網全長4 km,共設置16組如圖9所示模型,即每組0.25 km。

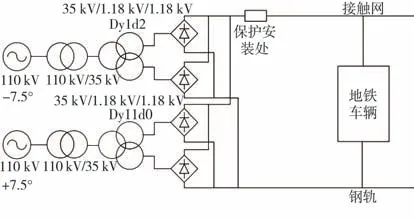
圖8 地鐵牽引系統仿真模型

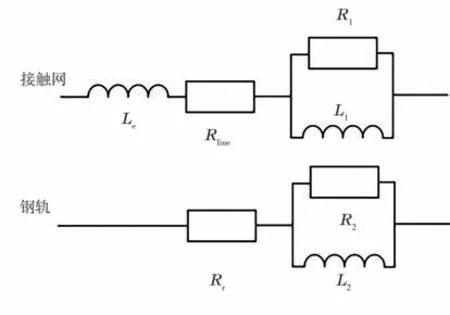
圖9 接觸網和鋼軌模型

采樣頻率設定為7 200 Hz,則24次諧波一周期有6個采樣點。基于所搭建模型及給定參數仿真可得正常運行時直流電流在2 500~3 000 A,本文取ID=3 000 A,故啟動判據的整定值ΔI Z=KSID/ms=180 A/ms。仿真得到I24max=3.18 A和I24min=0.91 A,取K1=0.6,K2=1.1,K3=1.2,因此由式(16)求得的保護整定值I Zmax=3.498 A、I Zmin=0.546 A。仿真中取ΔtP=0.2 s,地鐵車輛位置ls和故障發生位置lf分別指車輛以及饋線上的故障點到保護安裝處距離。

3.2 仿真結果分析

地鐵車輛正常運行至ls=2 km 時的饋線電流以及24次諧波電流幅值如圖10所示,正常運行時饋線電流中包含的24次諧波幅值較小。

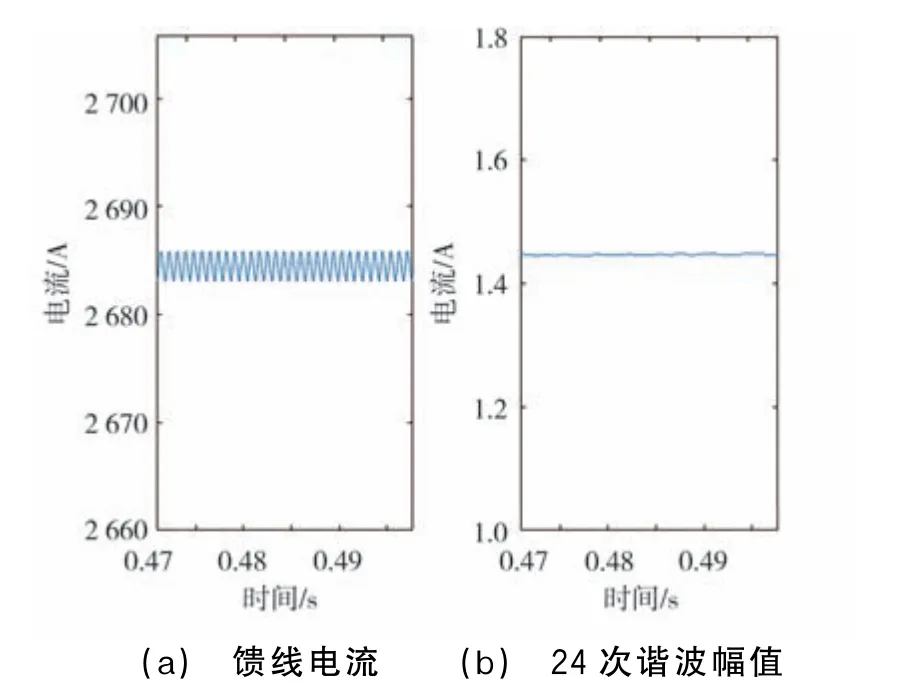
圖10 正常運行時饋線電流以及24次諧波電流幅值

地鐵車輛運行至ls=2 km 處時,在lf=0 km處發生故障時饋線電流的變化情況如圖11所示。故障發生的時刻為0.5 s。可以看出故障發生時刻饋線電流突然增長,故障起始時電流增長率為19 005.8 A/ms,遠大于ΔI Z=180 A/ms,啟動判據式(13)滿足,啟動元件動作。

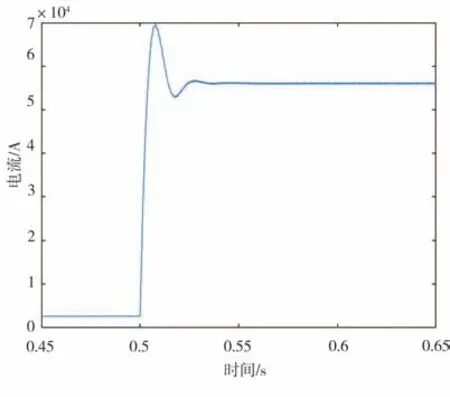
圖11 故障時饋線電流

由圖10 可知故障前24 次諧波電流幅值為I24=1.447 A,顯然I24>I Zmin。根據式(15)判定故障前有車輛行駛,保護應該用式(14)判據②且I ZN=K3I24=1.2×1.447 A=1.736 A。故障發生后延時ΔtP的24次諧波電流幅值見圖12,可以看出I t+ΔtP明顯大于I ZN,滿足式(14)判據②,保護動作。

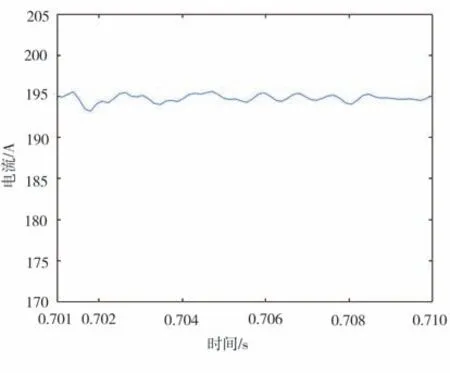
圖12 故障后24次諧波電流幅值

地鐵車輛于0.5 s時在ls=2 km 處升弓前后24次諧波電流的幅值如圖13所示。升弓時電流增長率為593.0 A/ms,該值遠大于啟動元件整定值ΔI Z=KSID/ms=180 A/ms,啟動元件動作。由于升弓前24次諧波電流幅值幾乎為零,根據式(15)判定為故障前無車輛行駛,保護應該用式(14)判據①。仿真結果如圖13所示,延時ΔtP后的24次諧波電流幅值I t+ΔtP遠小于I Zmax=3.498 A,不滿足判據①,保護不動作。

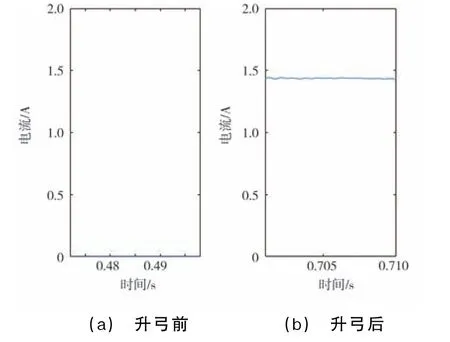
圖13 升弓前后24次諧波電流幅值

表2給出了不同故障情況下,故障前后24次諧波電流幅值以及保護的動作情況,均正確動作。

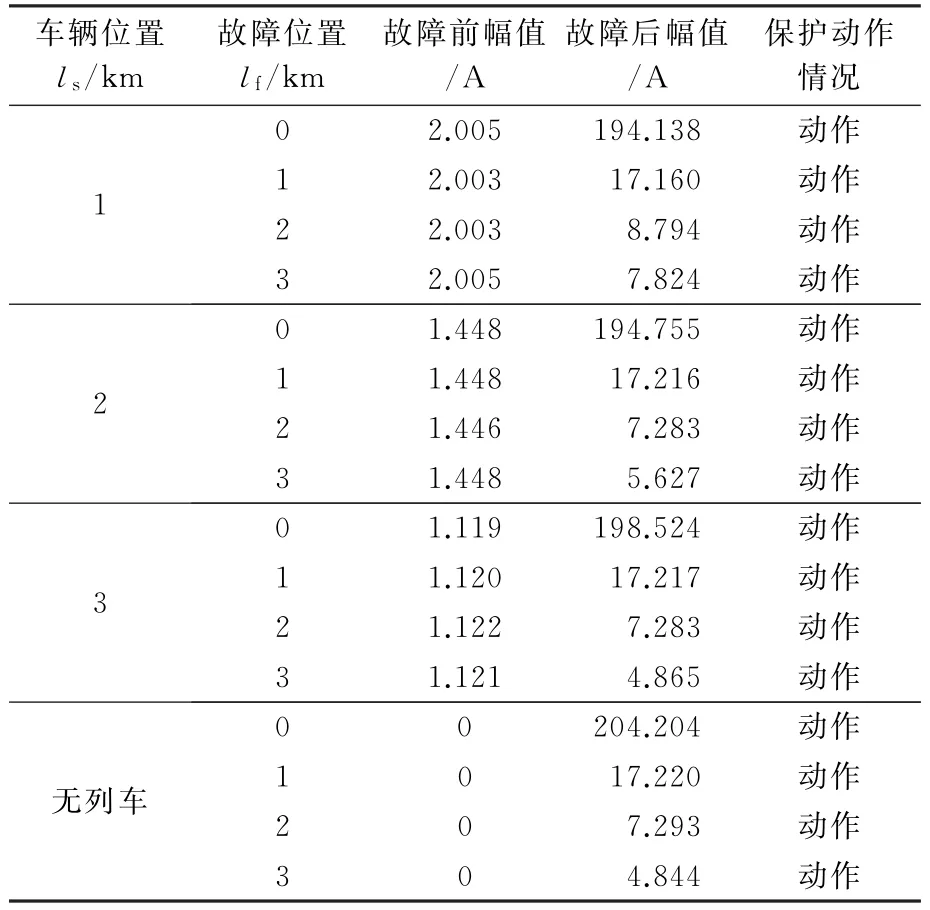
表2 不同故障情況下24次諧波電流幅值與動作情況

4 結論

本文分析了地鐵直流饋線上24次諧波的產生原因以及故障前后24次諧波電流的幅值變化情況,提出一種基于24次諧波電流幅值的地鐵直流饋線保護方案,可以作為直流饋線的后備保護。該方案具有原理清晰、易于實現的特點,不僅按照故障前有無車輛行駛情況設置保護動作判據,而且考慮了躲過升弓、過分段絕緣的影響,使得保護不會在這些情況下因電流變化而誤動作。