插層熔噴非織造材料的性能控制

尹堯夔,姜 蔚,劉嘉偉,常 亮

(西藏大學,拉薩 850000)

0 引言

熔噴非織造材料是口罩生產的重要原材料,具有較好的過濾性,成本低,質量輕,生產工藝簡單,受到了廣泛關注。但纖維使用過程中常因壓縮回彈性差而導致無法保證性能,故在聚丙烯熔噴制備過程中將滌綸短纖等纖維插入熔噴纖維流中,制備出了“Z型”結構的插層熔噴非織造材料。如果能夠分別建立工藝參數與結構變量、結構變量與產品性能之間的關系模型,將有助于建立產品性能調控機制。

研究工藝參數與結構變量之間的關系通常采用BP神經網絡算法對結構變量進行預測[1],運用信號的正向傳播輸入相關變量,使變量在輸入層上發揮作用,再進行隱層處理,進入誤差逆向傳遞階段,將傳遞誤差信息通過隱層向輸入層面逐級返回,獲得每層信息單元輸出產生的誤差信號,將誤差信號值作為修改各信息層信息單元權值的依據。建立一個三層的BP神經網絡模型,通過不斷輸入數據進行線性或非線性關系傳輸[2],對權重進行調整,重復循環,用輸出層的誤差調整輸出層權矩陣。建立工藝參數與結構變量之間的關系,預測固定數值的結構變量。

對數據進行預處理,將數據分為插層前與插層后,分別研究工藝參數與結構變量之間的關系。對數據進行擬合,比較優劣性,選擇最優數據。利用神經網絡模型中單層與多層神經網絡模式結構,將多個簡單變量并聯起來,形成神經元層。對數據之間的關系進行處理,通過BP神經網絡對數據進行反復訓練[3],建立函數進行數據擬合,對結構變量數值進行預測。

1 方案測試

輸入數據16個,即p=1,…,16;對應16個輸出,建立數學模型確定輸入層、中間層、輸出層及各層元素的數值,建立神經網絡系統。

設兩個權重系數矩陣為:

其中,wi(j,3)=θi(j)為閾值。

分析如下:

u1(1)=w1(1,1)a0(1)+w1(1,2)a0(2)+w1(1,3)a0(3)-θ1(1)

u2(1)=w1(2,1)a0(1)+w1(2,2)a0(2)+w1(2,3)a0(3)-θ1(2)

u3(1)=w1(3,1)a0(1)+w1(3,2)a0(2)+w1(3,3)a0(3)-θ1(3)

u4(1)=w1(4,1)a0(1)+w1(4,2)a0(2)+w1(4,3)a0(3)-θ1(4)

u5(1)=w1(5,1)a0(1)+w1(5,2)a0(2)+w1(5,3)a0(3)-θ1(5)

a1(1)=f[u1(1)]

a1(2)=f[u1(2)]

a1(3)=f[u1(3)]

a1(4)=f[u1(4)]

a1(5)=f[u1(5)]

將這兩個權重系數矩陣的分析結果作為第一層輸出,同時第二層的輸入為第一層輸出。其中,θi為閾值,f為激勵函數。若令a0(0)=-1(作為一固定輸入),w1(j,5)=θj,j=1,2,3,4,5(閾值作為固定輸入神經元相應的權系數),則有:

具體算法如下:令p=0

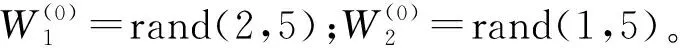
第二步:根據輸入數據,利用公式算出神經網絡的輸出:

第三步:計算:因為

δ2(1)=(t(1)-a2(1))f(u2(1))=(t(1)-a2(1))exp(-u2(1))/(1+exp(-u2(1)))2

第四步:取η=0.1(η>0),計算:

i,j=1,2,3,4,5

第六步:p=p+1,轉第二步。

注:僅計算一圈(p=1,2,…,15)會導致結果誤差較大、不準確,需直到各權重變化很小時再停止計算。

表1 BP神經網絡模型預測結果Tab.1 Prediction results of BP neural network model

2 結果檢驗和分析

神經網絡模型訓練結束后再次進行模擬檢驗,驗證模型預測結論的精確性[4]。以數據集的80%作為測試樣本,將所有測試數據樣本隨機輸入一個已初步訓練設定好參數的神經網絡模型數據庫中進行網絡實時仿真,對比數據真實輸出值及模型輸出真值之間的誤差,檢驗計算機網絡性能。研究表明,當BP神經網絡預測模型結果與實際結果的相對誤差小于0.05時,模型預測計算精度為良好。令數據集的80%作為訓練集,20%作為測試的屬性值集,計算屬性值集的中位數,利用中位數計算填充缺失部分的屬性值(注:中位數可通過訓練集的數據進行計算)。由于測試集只能作為模型間對于泛化誤差的一種近似,因此需要訓練好后在測試集上近似估計模型的泛化能力。驗證集要在選完合適的模型后逐一計算,利用人工驗證集確定神經網絡層數與神經元個數確定網絡模型經正則化驗證后的參數,通過測試集上的誤差來調節參數。

每次訓練都是隨機進行網絡初始化,數據誤差與訓練后的權值均存在數據差異,故每次訓練結束后產生的結果也存在誤差,無法達到100%的精確。將神經網絡預測與擬合方程得到的數據進行對比發現,方程擬合效果與預期值不匹配,神經網絡預測的結果更加理想,預測效果更加精確有效。

BP算法的改進可采取增加訓練集與測試集的方法,避免輸入層訓練過程中出現過擬合現象,使用智能啟發式算法優化神經網絡結構及權值閡值[5]增加訓練次數,盡量多進行訓練,降低網絡訓練失敗率。

3 最大過濾效率

過濾效率是產品性能評判的標準之一,且產品性能與結構變量有著密不可分的關系,故需研究結構變量與產品能之間的關系及結構變量之間、產品性能之間的關系,找到某工藝參數條件下的最大過濾效率。由于部分變量數據相差較大,對大數據進行降維再繪圖,可直觀看出各變量之間的關系。為了避免出現較大的誤差,建立求解關系的回歸模型,當函數做回歸分析計算有兩個變量及兩個以上的自變量函數時,回歸分析結果可稱為函數多元回歸[6],需研究產品過濾效率與工藝參數之間的最值問題,利用自變量的最優組合進行預測,結果要比一般的單變量估計預測更符合實際。

Y=β0+β1x+β2x2+…+βpxp+ε構建的關于變量x,Y的線性回歸模型中,p是已知的參數,βi(i=1,2,…,p)是未知參數,ε服從正態分布N(0,σ2)。

3.1 計算機實現與計算方法設計

對部分數據進行降維,通過Excel對各個變量關系進行繪圖。通過SPSS 25.0進行關系驗證。將數據排序處理,再導入MATLAB中,利用rstool函數判斷多元二項式回歸方程的顯著性[7]。將數據代入方程求解β0,β1,β2,β3,β4。通過數據處理得到工藝參數與結構變量之間的可移動關系,其他變量關系也由此推出。

3.2 方案測試結果

通過Excel對各個變量的關系進行繪圖,如圖1所示。

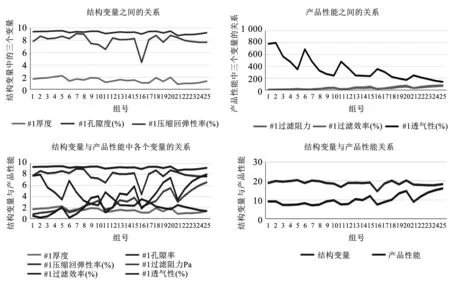
圖1 各變量關系Fig.1 Relationship between variables

由圖1分析各個變量之間的關系如下:結構變量與產品性能變化趨勢基本一致,只有部分數據稍有差異,但并不影響二者的關系。結構變量中厚度與孔隙度相關性較高,變化幅度基本一致,壓縮回彈性率與二者的相關性不高,壓縮回彈性變化幅度較大,而厚度與孔隙度變化幅度較小。產品性能中過濾效率與透氣性相關性高,二者變化幅度基本一致,過濾阻力與二者沒有明顯關系,但是過濾阻力的變化具有周期性變化,符合先增后減的規律。

通過SPSS 25.0對各個變量之間的關系進行驗證,結果如下:結構變量與產品性能相關性較高,符合前面總結的基本關系[8]。厚度與孔隙率的雙尾系數為0.000 0,相關性并不顯著。厚度與壓縮回彈性率的雙尾系數為0.048,接近0.05,相關性顯著。孔隙率與壓縮回彈性率的雙尾系數為0.053,接近0.05,相關性顯著。由此可知,可視化分析的基本關系稍有偏差,厚度與壓縮回彈性率的相關性高,孔隙率與壓縮回彈性高,而厚度和孔隙度之間相關性不顯著。

過濾阻力與過濾效率呈正相關關系,過濾阻力與透氣性呈負相關關系,過濾效率與透氣性呈負相關關系,這與可視化分析得到的基本關系有輕微偏差。

通過MATLAB得到工藝參數與結構變量之間的回歸模型:

將數據代入上述回歸模型,得到周期函數,如圖2所示。

圖2 周期函數Fig.2 Periodic function graph

結果分析:接受距離為實驗時溶液噴射點到接收噴射過來的溶液位置的距離大于零,由圖像可得周期函數為n個遞減函數,當接受距離取3 cm、熱風速度取980 r/min時,達到最高效率。但是當接受距離太小時布脆強力會下降,需結合熱風速度等其他參數進行共同調整。實驗表明,當接受距離為30 cm、熱風速度為910 r/min時,產品過濾效率達到最高。

3.3 結果檢驗

線性模型和回歸系數的檢驗回歸方程:

Y=β0+β1x+β2x2+…+βkxk

假設H0:β0=β1=β2…βk=0。常見的檢驗方法包括F檢驗法和r檢驗法,其中F檢驗法通常需要計算回歸平方和與殘差平方和,r檢驗法通常使用等效的方法進行檢驗。

3.4 模型優化

利用逐步回歸分析法的數學思想[9]建立回歸模型,通過自變量Y值對回歸作用影響程度進行排序,按照從大到小的順序依次建立相應的回歸方程。引入每一個自變量時都會使被引入后面的所有變量出現不太顯著的結果,需要將變量與對應結果刪掉,不計入方程中。逐步回歸分析法的關鍵是令某一個自變量重新引入或重新刪除,不斷循環這個過程,從而引出回歸方程[10]。本模型從多方面進行改進,從多個變量同時分析對變量Y的顯著程度,可避免單個變量對結果的誤差影響[11],但是操作較困難。

4 結束語

對熔噴非織造材料建立了工藝參數與結構變量、結構變量與產品性能之間的關系模型,數據及模擬較為準確。利用MATLAB進行數學建模,可幫助理解計算模型及相應的數據統計分析,具有一定的推廣價值。