基于數字巖石物理技術的裂隙方向對地震波速度影響規律研究

許可 高啟 楊俊杰 朱偉 郝龍

摘 要：【目的】研究裂隙方向對地震波傳播速度的影響。【方法】基于數字巖石物理技術，建立含裂隙數字巖心，并變化裂隙方向，計算縱、橫波速度；研究裂隙為水飽和與干燥時數字巖心的縱、橫波速度與裂隙方向之間的關系。【結果】數值模擬研究發現，即使裂隙含量較小的情況下，裂隙方向的變化對地震波的傳播速度具有較大的影響。【結論】研究成果對裂隙發育區的地震資料解釋具有重要指導意義。

關鍵詞：數字巖心；裂隙；各向異性；速度

中圖分類號：P631.4? ? ? ? 文獻標志碼：A? ? ? ? 文章編號：1003-5168（2023）10-0114-04

DOI：10.19968/j.cnki.hnkj.1003-5168.2023.010.024

Abstract： [Purposes] The influence of fracture direction on seismic wave propagation velocity is studied. [Methods] Based on the digital rock physics technology， the digital core with fracture was established， and the fracture direction was changed to calculate the longitudinal and transverse wave velocities. The relationship between the P-wave and S-wave velocities of the digital core and the fracture direction whether the fracture is saturated by water or just dry is studied. [Findings] The numerical simulation result shows that even if the crack volume is small， the change of crack-direction has a great influence on the seismic velocity. [Conclusions] The result has important guiding significance for seismic data interpretation in areas with cracked formations.

Keywords： digital rock; crack; anisotropy; velocity

0 引言

裂隙在地殼淺處的地層巖石中普遍存在。裂隙和裂隙、裂隙和孔隙相互連通，是油、氣和水在地下運移的通道。裂隙對油氣開采至關重要，儲集體往往需要人工壓裂生成裂隙網絡，便于油氣向井孔方向流動，實現高產穩產。

裂隙的體積小、延伸范圍廣，對地震波的傳播速度可能存在較大影響。無論是縱波還是橫波，傳播方向和裂隙方向之間的夾角發生變化時，波的傳播速度可能會發生明顯改變。裂隙可能使橫波產生橫波分裂現象。當橫波平行裂隙面傳播時，若偏振方向與裂隙面斜交，橫波可分解為兩個傳播速度不同的橫波。偏振方向平行裂隙面的橫波傳播速度快，偏振方向垂直裂隙面的橫波傳播速度慢［1］。裂隙排列引起的地層彈性的各向異性和橫波分裂現象是發現高滲儲層的重要指示。

由于裂隙在油氣勘探和開發中的重要作用，研究裂隙方向變化對地震波傳播速度的影響具有重要意義。現有研究方法包括物理試驗、理論計算和數字巖石物理。物理試驗的周期長、成本高、技術難度大［2-3］。理論計算的假設和限制條件較多［4-6］。數字巖石物理技術可以靈活地設計相當數量的數字巖心，計算彈性參數，統計彈性參數與裂隙參數之間的關系［7-10］。鑒于數字巖石物理技術的優勢，本研究采用該技術研究裂隙方向變化對縱、橫波速度的影響規律。

1 數字巖石物理技術的基本原理

數字巖心是由像素構成的，每一個像素均是一個立方體網格。不同的像素可以表示不同的物質，如石英礦物、孔隙液體和氣體等。當研究孔隙尺度的結構非均勻性引起的數字巖心的宏觀各向異性時，每個像素的彈性性質都是各向同性的。數字巖心宏觀彈性性質可利用有限元靜力學方法計算，其基本原理是在數字巖心的表面加載應變（位移）邊界條件，計算初始彈性勢能，通過共軛梯度法求解最小彈性勢能對應的應力與應變狀態，計算平均應變張量和平均應力張量，反推數字巖心的彈性模量［7-9］。

當設置了初始條件和邊界條件，數值迭代結束后可以統計出數字巖心的6個平均應力分量ε11，ε22，ε33，ε12，ε23，ε31和6個平均應變分量ε11，ε22，ε33，ε12，ε23，ε31。此處有如下對應關系：[1?x，2?y，3?z]。[x，y]和[z]表示直角坐標系中的三個坐標軸。由于是對應變進行了設置，故最終統計的6個平均應變分量的值就是模擬設置的值。改變初始條件和邊界條件，可以計算相應的彈性模量。

當計算了彈性模量，縱、橫波速度的公式計算見式（7）、式（8）。

2 數字巖心及其模擬結果

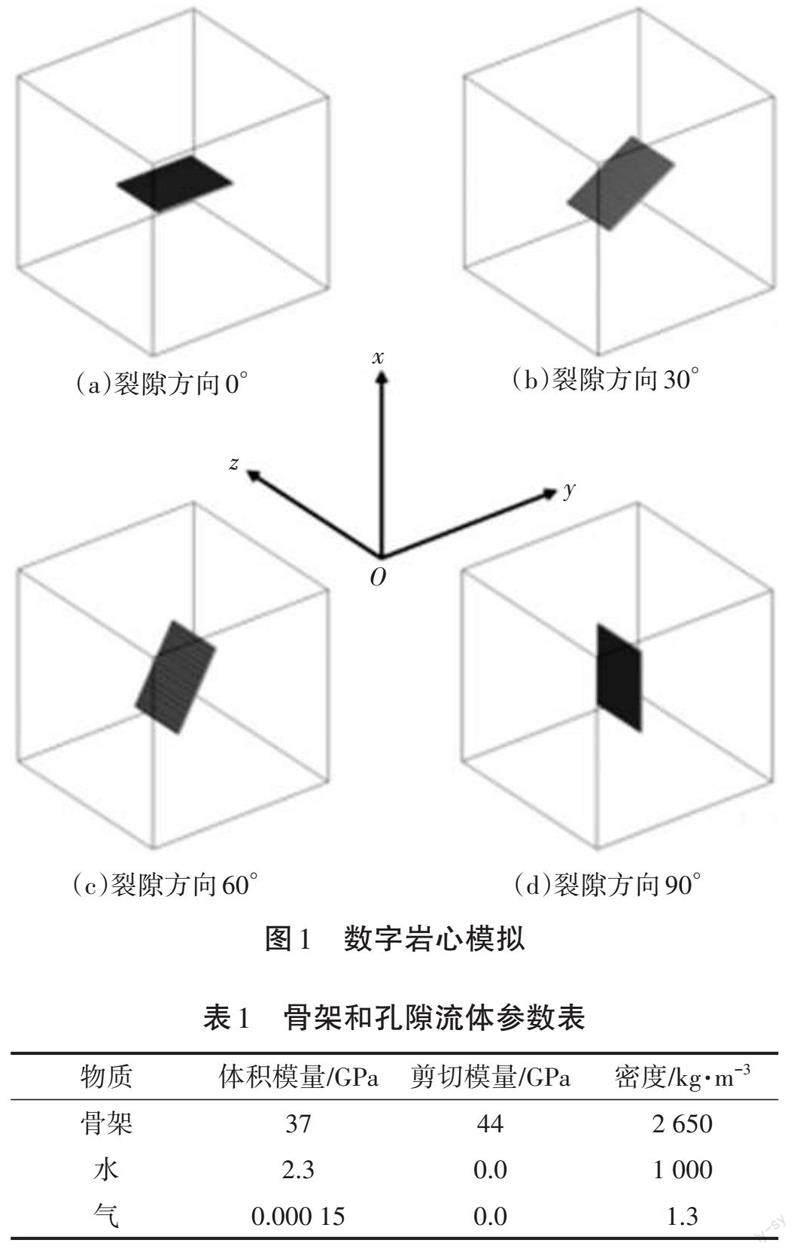
數字巖心模擬如圖1所示，大小均為280×280×280像素，包含一個平面矩形裂隙。從圖1（a）至圖1（d），裂隙面的法方向與x軸的夾角分別是0°、30°、60°和90°，下文稱之為裂隙方向（角度）；數字巖心的孔隙度分別是0.195 2%、0.192 7%、0.192 7%和0.195 2%。

數值模擬中，令裂隙飽和水或氣，分別計算出水飽和和氣飽和數字巖心的彈性模量。數字巖心的骨架和孔隙流體的參數見表1。

數值模擬結果如圖2所示。圖中的橫坐標crack angle為裂隙角度。圖例中saturated表示裂隙為水飽和，dry表示裂隙為氣飽和。由于氣體的體積模量和密度極小，可認為數字巖心為干燥。

在圖2（a）中，沿z方向傳播的縱波速度[VPz]與裂隙角度無關。因為縱波傳播方向始終與裂隙面平行。裂隙流體充填情況對縱波速度的影響極小。

在圖2（b）中，沿y方向傳播的縱波速度[VPy]隨裂隙角度的增大而減小。裂隙角度為0°時，縱波傳播方向與裂隙面平行，故速度最大。裂隙角度為90°時，縱波傳播方向與裂隙面垂直，故速度最小。裂隙角度越大，干燥和飽和數字巖心的縱波速度差異越大，且干燥的縱波速度小于飽和的縱波速度。

在圖2（c）中，x方向傳播的縱波速度[VPx]隨著裂隙角度的增大而增大。裂隙角度為0°時，縱波傳播方向與裂隙面垂直，故速度最小。裂隙角度為90°時，縱波傳播方向與裂隙面平行，故速度最大。裂隙角度越小，干燥和飽和數字巖心的縱波速度差異越大，且干燥的縱波速度小于飽和的縱波速度。

在圖2（d）中，[VSxy]表示沿x（y）方向傳播，偏振方向沿y（x）方向的橫波速度。當裂隙方向為0°和90°時，表示橫波傳播方向垂直裂隙面，偏振方向平行裂隙面；或橫波傳播方向平行裂隙面，偏振方向垂直裂隙面，故橫波速度為最小值。當裂隙為30°和60°時，橫波速度稍稍增大。水飽和數字巖心的橫波速度變化大于干燥數字巖心的橫波速度變化。

在圖2（e）中，[VSyz]表示沿y（z）方向傳播，偏振方向沿z（y）方向的橫波速度。橫波速度隨著裂隙角度的增大而減小。當裂隙角度為0°時，橫波的傳播方向和偏振方向均平行裂隙面，故橫波速度最大。當裂隙角度為90°時，表示橫波傳播方向垂直裂隙面，偏振方向平行裂隙面；或橫波傳播方向平行裂隙面，偏振方向垂直裂隙面，故橫波速度最小。干燥和水飽和的數字巖心的橫波速度差異極小，干燥的速度稍大。

在圖2（f）中，[VSzx]表示沿z（x）方向傳播，偏振方向沿x（z）方向的橫波速度。橫波速度隨著裂隙角度的增大而增大。當裂隙角度為0°時，表示橫波傳播方向垂直裂隙面，偏振方向平行裂隙面；或橫波傳播方向平行裂隙面，偏振方向垂直裂隙面，故橫波速度最小。當裂隙角度為90°時，橫波的傳播方向和偏振方向均平行裂隙面，故橫波速度最大。干燥和水飽和的數字巖心的橫波速度差異極小，干燥的速度稍大。

由于裂隙方向平行xoy平面，沿x方向和沿y方向傳播的縱波速度具有互補關系；[VSyz] —裂隙角度的關系和[VSzx] —裂隙角度的關系具有互補關系。

3 結論

本研究建立了4個包含平面裂隙的數字巖心，采用各向異性的有限元靜力學數值模擬方法，分別計算3個方向的縱波模量和3個方向的橫波（剪切）模量。當變化裂隙的方向時，縱波速度和橫波速度對裂隙方向均有明顯的反應，并且與裂隙中流體的類型有關。研究結論對裂隙發育地區的地震資料解釋具有重要指導作用。

參考文獻：

［1］丁文龍，姚佳利，何建華，等.非常規油氣儲層裂縫識別方法與表征［M］.北京：地質出版社，2015.12.

［2］GUO J X， SHUAI D，WEI J X，et al. P-wave dispersion and attenuation due to scattering by aligned fluid saturated fractures with finite thickness： theory and experiment. Geophysical Journal Internationa［J］. 2018.215（3）：2114-2133.

［3］丁拼搏，秦菽苑，劉海浩，等.單裂縫不同傳播方向Krauklis波振幅變化的實驗研究［J］.地球物理學報，2019，62（12）：4794-4804.

［4］MAVKO G， MUKERJI T， DVORKIN J. The rock physics handbook： Tools for seismic analysis of porous media［M］. Cambridge： Cambridge University Press，2009.

［5］Guo JX，GUREVICHB，SHUAI D，Frequencydependent P-wave anisotropy due to scattering in rocks with alignedfractures. Geophysics［J］. 2020.85（2）：MR97-MR105.

［6］郭俊鑫，方鑫定.含平行裂縫儲層中地震波頻散，衰減及頻變各向異性［J］.應用聲學，2020，39（1）：11.

［7］GARBOCZI E J. Finite element and finite difference programs for computing the linear electric and linear elastic properties of digital images of random materials［R］. National Institute of Standards and Technology，1998.

［8］ARNS C H， KNACKSTEDT M A， PINCZEWSKI W V， et al. Computation of linear elastic properties from microtomographic images： Methodology and agreement between theory and experiment［J］. Geophysics， 2002，67（5）：1396-1405.

［9］朱偉，於文輝.CPU-GPU異構并行計算在數字巖心線彈性靜力學有限元模擬中的應用［J］.地球物理學進展，2016（4）：6.

［10］趙建國，潘建國，胡洋銘，等.基于數字巖心的碳酸鹽巖孔隙結構對彈性性質的影響研究（上篇）：圖像處理與彈性模擬［J］.地球物理學報，2021，64（2）：656-669.

收稿日期：2023-02-13

作者簡介：許可（1998—），男，碩士生，研究方向：數字巖心。