旋轉部件熱套緊量選取及仿真驗證

肖 雷

（東方電氣集團東方電機有限公司，四川 德陽 618000）

1 旋轉部件離心力分析

1.1 集電環套筒離心應力和位移

集電環也稱滑環，是同步電機的關鍵部件之一，與刷架、電刷、轉子繞組和軸配合完成同步電機轉子電能的輸入，并提供轉子旋轉磁場。目前的同步電機集電環普遍為集電環套筒整體套裝在軸上，然后在集電環套筒上包扎、固化絕緣，加工后將集電環套裝到包有絕緣的集電環套筒上。其中，集電環、絕緣套筒和轉軸之間都是典型的過盈配合結構，即熱套結構。

該文以某同步電動機集電環套筒為例，并在超速工況下計算、討論旋轉部件熱套緊量的選取問題。其中集電環套筒材料為Q235 鋼，軸材料為高質量合金鋼。集電環套筒外形如圖1 所示，具體尺寸見表1。

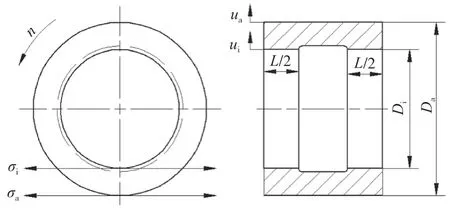
圖1 集電環套筒

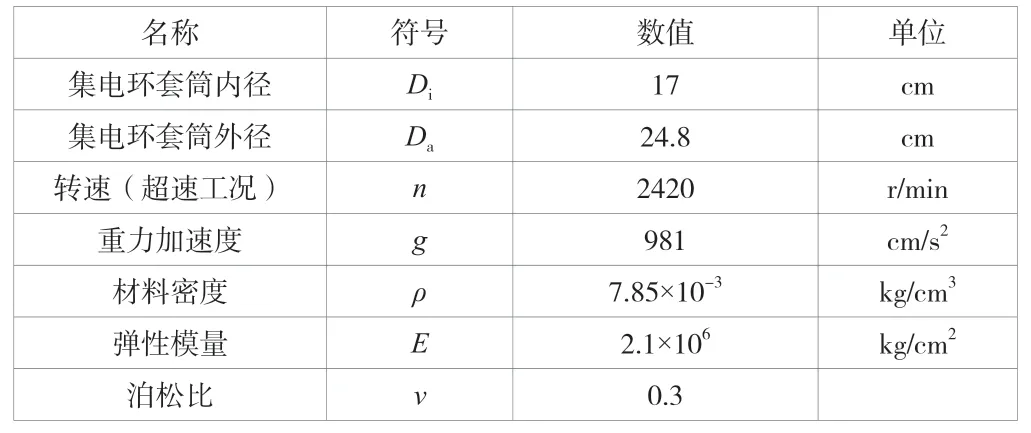
表1 集電環套筒數據

集電環套筒承受離心力時的計算如公式（1）～公式（3）所示。

集電環套筒外圓表面徑向位移如公式（5）所示。

集電環套筒內圓表面切應力如公式（6）所示。

從公式（1）到公式（7）可以看出，旋轉部件應力、位移僅與材料密度和轉速有關，與熱套接觸長度無關，即增大熱套接觸尺寸不能改善集電環套筒熱套強度。熱套長度會影響傳遞力矩的大小及拆卸難度，后文將詳細論述。

在集電環套筒內圓確定的情況下，k越大，內圓與外圓尺寸越相近，內外圓應力、位移也越接近，材料的利用率也就越高。考慮既要滿足材料應力要求，又要提高材料利用率，一般取k＞0.6，部分大型電機甚至取k＞0.8。

由于接觸尺寸長度與圓環強度無關，因此取集電環套筒部分切面進行有限元分析，計算結果見表2。

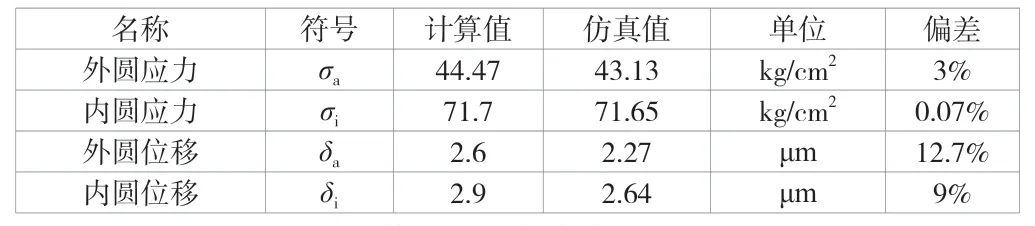
表2 集電環套計算結果與仿真結果對比

1.2 與集電環配合的軸面離心應力和位移

與集電環套筒離心力應力和位移計算方法相同。與集電環配合的軸如圖2 所示。

圖2 與集電環配合的軸

軸外圓表面切應力及外表面徑向位移如公式（8）、公式（9）所示。

公式（8）～公式（9）的計算結果與仿真結果對比見表3。

表3 軸計算結果與仿真合應力結果對比

1.3 最小過盈量

采用溫差法進行裝配時，配合表面微觀不平度被擦平得較少，可忽略不計，因此單邊最小實際過盈量如公式（10）所示。

采用壓入法進行裝配時，配合表面微觀不平度的波峰總會被擦傷或壓平一部分，壓平部分通常取兩配合表面粗糙度RZ的60%，即在半徑上增加0.6（Rzi+Rzo），因此單邊最小實際過盈量如公式（11）所示。

該例中，集電環套筒與軸之間采用熱套裝配，因此最終集電環套筒配合面取?170H7（+0.040），軸配合面取?170r6（+0.093+0.068），單邊最小過盈量δmin為（1.4×10-3）cm，單邊最大過盈量δmax為（4.65×10-3）cm。

2 熱套后應力分析

熱套結束后，集電環套筒與軸之間的相互作用力如圖3 所示，配合面為最大過盈量時的接觸壓力如公式（12）所示。

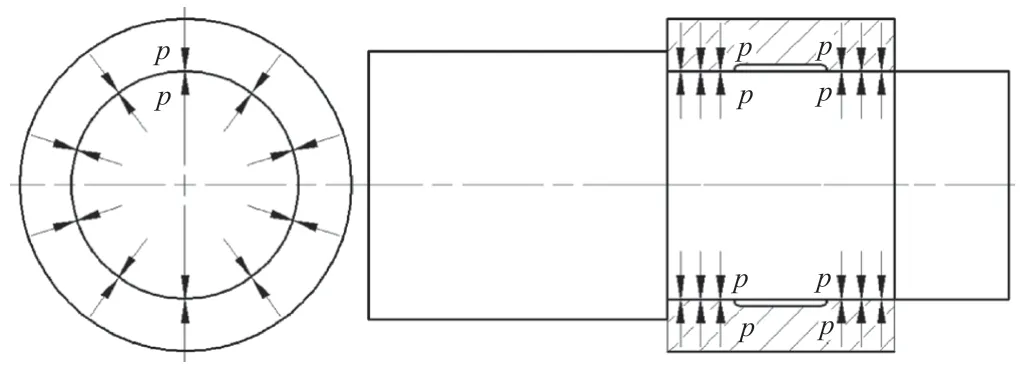
圖3 過盈配合

該公式僅適用于轉軸為實心的情況。

集電環套筒配合面切向應力如公式（13）所示。

軸配合面切向應力如公式（14）所示。

式中：負號代表壓應力。

同理可求得最小過盈量切徑向應力，見表4。

表4 熱套后應力（單位：kg/cm2）

過盈配合仿真模型及應力結果如圖4 所示。圖4 的仿真是基于內應力的仿真，取的是集電環套筒及軸部分切面，仿真結果和理論結果相差不大。現實中由于邊界的存在，因此結果會有所差異。

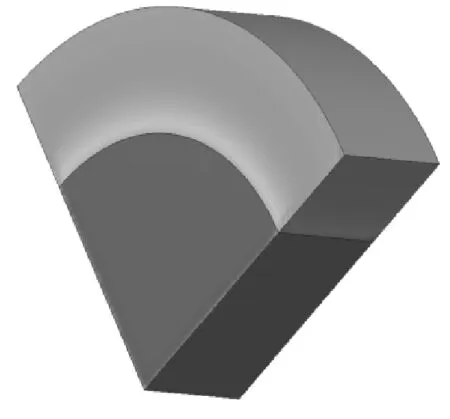
圖4 過盈配合仿真模型及應力結果

在實際工程應用中，為了降低拆裝難度，會采取集電環套筒與軸兩端配合且中間不接觸的設計。這種結構在裝配完成后，在配合面和非配合面的交界處會出現應力集中的情況。配合長度越長，配合段中部的壓強值越接近理論計算值。配合長度越小，應力集中峰值就越大，其變化規律近似于線性關系。配合長度越短，配合段內的接觸壓力平均值就越高。

該文所講示例的最小過盈量、最大過盈量仿真結果見表5、表6。其中接觸壓力是作用在接觸面上的作用力與反作用力，因此套筒配合面與軸配合面接觸壓力本應相等。由于集電環套筒中間段不與軸配合，接觸面上應力分布不均，存在由接觸引起的邊緣應力集中，因此仿真結果中套筒配合面與軸配合面的平均接觸壓力出現了差別。

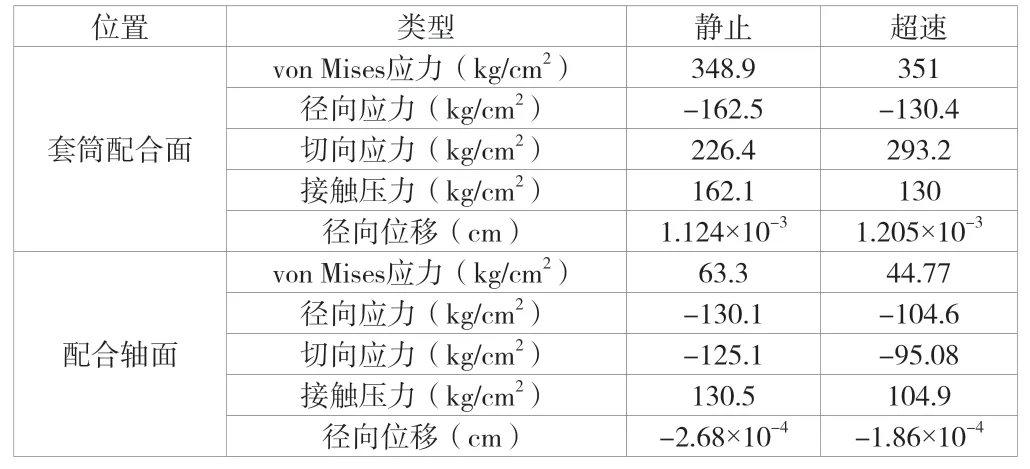
表5 最小過盈量仿真結果（接觸面平均值）

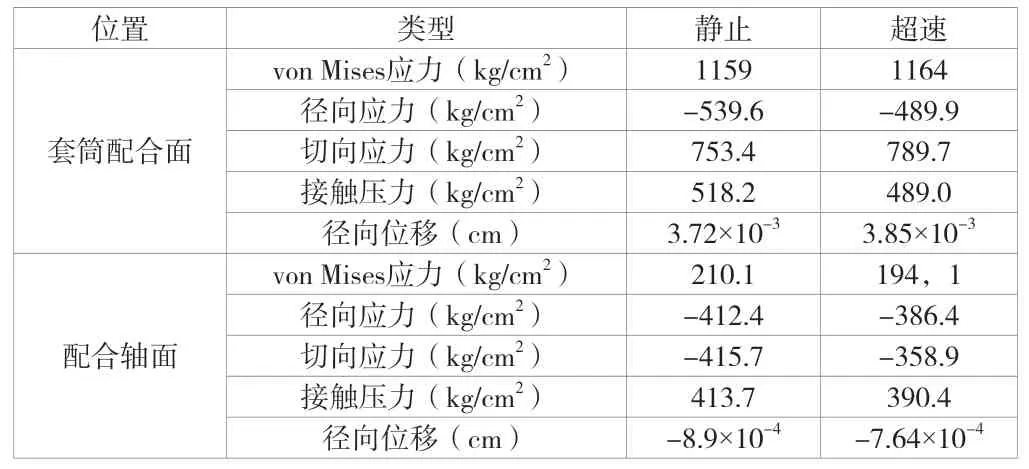
表6 最大過盈量仿真結果（接觸面平均值）

另外從有限元仿真可以看出，集電環套筒和軸的過盈聯接存在邊緣效應，邊緣應力的值大大高于彈性力學的解。基于彈性力學理論獲得的應力結果沒有考慮集電環套筒接觸邊緣的變化引起的應力集中，具有一定的局限性，特別是壽命計算會與實際情況偏差較大。彈性力學獲得的解析解只能與有限元的平均值進行比較。目前經典力學尚無法求解包容件邊緣應力的變化，而邊緣應力集中將直接影響聯接的強度和壽命。解析法與有限元法應結合使用，才是精確分析集電環套筒的應力及疲勞的有效方法。

如果集電環套筒邊緣應力集中系數較大，應采取開卸載槽的措施，減少應力集中，并提高聯接的可靠性和疲勞壽命。

3 集電環套筒裝配

溫差裝配法是利用材料熱脹冷縮的性能加熱包容件或冷卻被包容件，或二者同時進行的方法。配合件在溫差條件下失去過盈量，從而實現自由裝配，待溫差消失后即形成緊配合[1]。裝配溫度計算如公式（15）所示。

式中：t為裝配時包容件加熱溫度；t0為環境溫度；δ為實測最大過盈量；δ0為熱套單邊最小間隙，取0.1mm；α為包容件線漲系數；dk為包容件線內徑。

4 集電環套筒拆卸

過盈聯接的裝配方法按原理不同可分為壓入法、脹縮法和油壓法[2]。不同的裝壓方法摩擦系數不同，導致拆裝力也不同。由于影響摩擦系數的因素較多，如聯接件材料、裝配方式、潤滑油、粗糙度和過盈量等，因此會導致摩擦系數變化范圍很寬，獲得精確摩擦系數的難度也較大。在非精準計算的情況下，不同材料過盈聯接接觸面摩擦系數見表7。

過盈聯接件因本身結構特性，拆卸時存在較大困難，工作表面易被劃傷，甚至因無法拆卸而只能破壞性拆除。拆卸集電環套筒時一般使用千斤頂。如果千斤頂就位，集電環套筒仍無松動跡象，需要加熱集電環套筒。但加熱時間不得太長，不得讓熱傳至主軸。拆卸時需要的最大壓出應力（最大過盈量）如公式（16）所示。

式中：L為有效配合面長度，單位cm。

拆卸時需要的最小壓出應力（最小過盈量）如公式（17）所示。

該文所講示例的拆卸力見表8、表9。

表8 最大過盈量時集電環套筒拆卸力

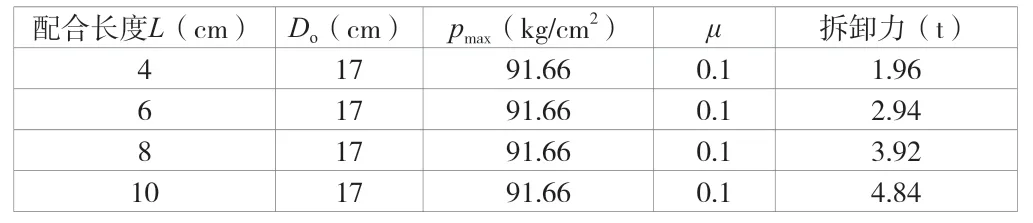
表9 最小過盈量時集電環套筒拆卸力

從表8、表9 可以看出，配合長度L雖與集電環套筒應力無關，但對集電環套筒的拆卸有極大影響。

真實模型有限元仿真結果如圖5 所示。從圖5 可以看出，集電環套筒及配合軸面應力主要集中在配合面邊線上，兩邊線之間部分較小，所以配合長度L的取值不需要很大。

圖5 真實模型仿真應力

5 轉遞載荷所需最小接觸壓力

過盈部件僅傳遞軸向力Fa時所需的最小接觸壓力如公式（18）所示。

過盈部件僅傳遞力矩M時所需的最小接觸壓力如公式（19）所示。

過盈部件同時傳遞軸向力Fa和力矩M時所需的最小接觸壓力如公式（20）所示。

從公式（18）～公式（20）可以看出，接觸長度L在極大程度上會影響過盈部件傳遞力及力矩的大小。集電環套筒設計時還需要考慮所裝配的集電環力矩的大小。

6 結語

該文通過解析法和有限元法，以集電環套筒熱套緊量的選取為例，介紹了旋轉部件離心力的計算、熱套緊量的選取、配合面應力計算、拆卸力以及傳遞載荷等情況，為旋轉部件熱套尺寸的選取提出了建議。該文通過解析法和有限元法對比，得出經典力學求解的理論值只能與有限元的平局值相對應的結論，經典力學在處理邊緣效應上具有一定的局限性。可以將經典力學的結果作為設計參考，同時還需要配合有限元法核算應力和疲勞。在應力集中系數較大的情況下，需要開卸載槽來緩解應力集中。另外，溫度分布不均勻會影響過盈量大小，零件內部產生熱應力、工作環境溫度過高、裝配溫度間有差異、材料線彈性系數不同也會影響過盈聯接的性能。該文例子中集電環套筒材料與軸材料線脹系數相差不大，因此熱應力的影響可以忽略。