桑樹坪井田構(gòu)造復(fù)雜程度預(yù)測
——以未采區(qū)3#煤層為例
羅偉強(qiáng) 魯 琪
(1.中煤西安設(shè)計(jì)工程有限責(zé)任公司,陜西 西安 710054;2.陜西煤田地質(zhì)勘查研究院有限公司,陜西 西安 710021)
煤炭開采過程中,復(fù)雜的地質(zhì)構(gòu)造是影響高效合理采煤的重要因素之一[1]。研究者主要運(yùn)用了熵函數(shù)法、灰色模糊綜合評(píng)價(jià)法[2-3]對(duì)地質(zhì)構(gòu)造復(fù)雜程度做了大量研究,但這些方法過多局限使用于地質(zhì)條件已知或半已知區(qū),而未采區(qū)構(gòu)造規(guī)律不清,科學(xué)預(yù)測難度較大。為解決這一問題,該文以桑樹坪井田未采區(qū)3#煤為研究對(duì)象,應(yīng)用了熵函數(shù)與模糊綜合評(píng)判相結(jié)合的方法,預(yù)測了未采區(qū)構(gòu)造復(fù)雜程度,旨在為礦井提供合理的采掘建議和理論指導(dǎo)。
1 地質(zhì)概況
韓城礦區(qū)桑樹坪井田位于祁呂賀山字型構(gòu)造前弧東翼邊緣和秦嶺陰山2 個(gè)構(gòu)造帶之間,地質(zhì)構(gòu)造復(fù)雜,3#煤層已揭露斷裂構(gòu)造高到63 條,主要以df1、df2、df3為主,局部斷層小且密集,主要分布在井田中東部及東南部位置。在整個(gè)井田范圍內(nèi),褶皺構(gòu)造發(fā)育,從南向北依次排列f1向斜、f2背斜、f3向斜、f4背斜、f5向斜,斷裂構(gòu)造多沿褶皺軸部地區(qū)展布,也是造成本區(qū)構(gòu)造復(fù)雜化的主要原因之一[4-5]。
2 已采區(qū)3#煤層熵值計(jì)算
基于熵函數(shù)法對(duì)3#煤層已采區(qū)進(jìn)行熵值計(jì)算,基本流程:等性網(wǎng)格劃分→網(wǎng)格單元地學(xué)信息統(tǒng)計(jì)→網(wǎng)格單元賦值→網(wǎng)格單元熵函數(shù)計(jì)算。
2.1 網(wǎng)格單元?jiǎng)澐?/h3>
結(jié)合3#煤層綜采的要求、煤層的賦存規(guī)律,及研究區(qū)域內(nèi)構(gòu)造線走向,確定了網(wǎng)格單元的布置形式及尺寸:200m×200m。全井田范圍內(nèi)共劃分塊網(wǎng)格單元1322 個(gè)。已采區(qū)占318 個(gè)網(wǎng)格單元,如圖1 所示。
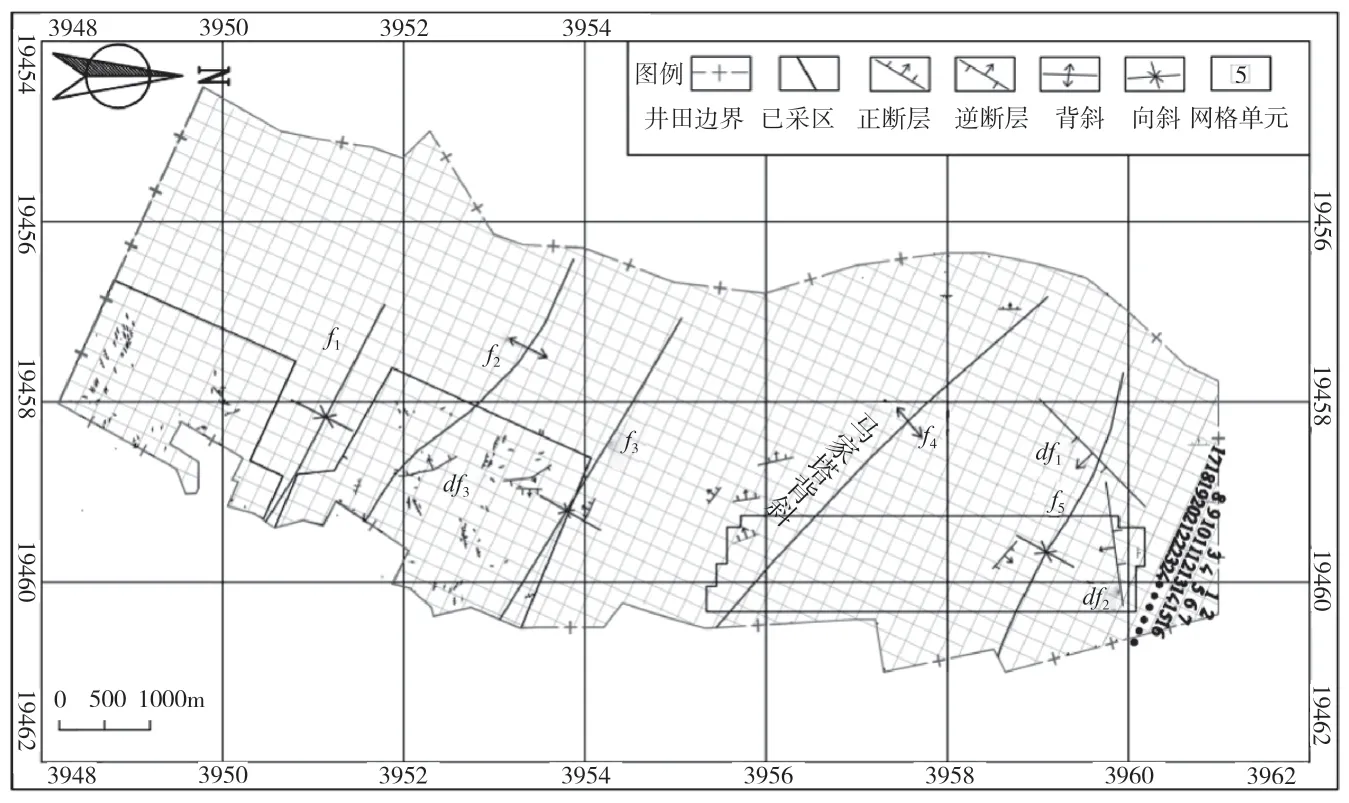
圖1 網(wǎng)格單元?jiǎng)澐?/p>
2.2 熵值計(jì)算
熵函數(shù),自從玻耳茲曼(L.Boltzmann)提出以后,已在生物學(xué)、氣象學(xué)等領(lǐng)域得到廣泛應(yīng)用[5]。
熵函數(shù)通常用公式(1)表示。
式中:S為系統(tǒng)的熵;Pi為系統(tǒng)中i狀態(tài)出現(xiàn)的概率;N為系統(tǒng)中狀態(tài)數(shù)。
為了消除系統(tǒng)狀態(tài)不同對(duì)系統(tǒng)熵的影響,引入相對(duì)熵的概念,如公式(2)所示。
式中:S′為系統(tǒng)的相對(duì)熵;Smax為系統(tǒng)的最大熵值。
在信息理論中,信息熵是指信息在傳播中的不確定性,高信息度的信息熵是很低的,所以,可認(rèn)為熵函數(shù)的熵值越小構(gòu)造越復(fù)雜,熵值越大構(gòu)造越簡單。
3#煤層已采區(qū)熵值的計(jì)算應(yīng)遵循斷層和褶皺規(guī)模越大其賦值越大的原則,見表1[6]。根據(jù)熵值計(jì)算公式(1)、公式(2)對(duì)各個(gè)網(wǎng)格單元的相對(duì)熵值進(jìn)行計(jì)算,部分熵值結(jié)果見表2,熵值等值線圖如圖2 所示。
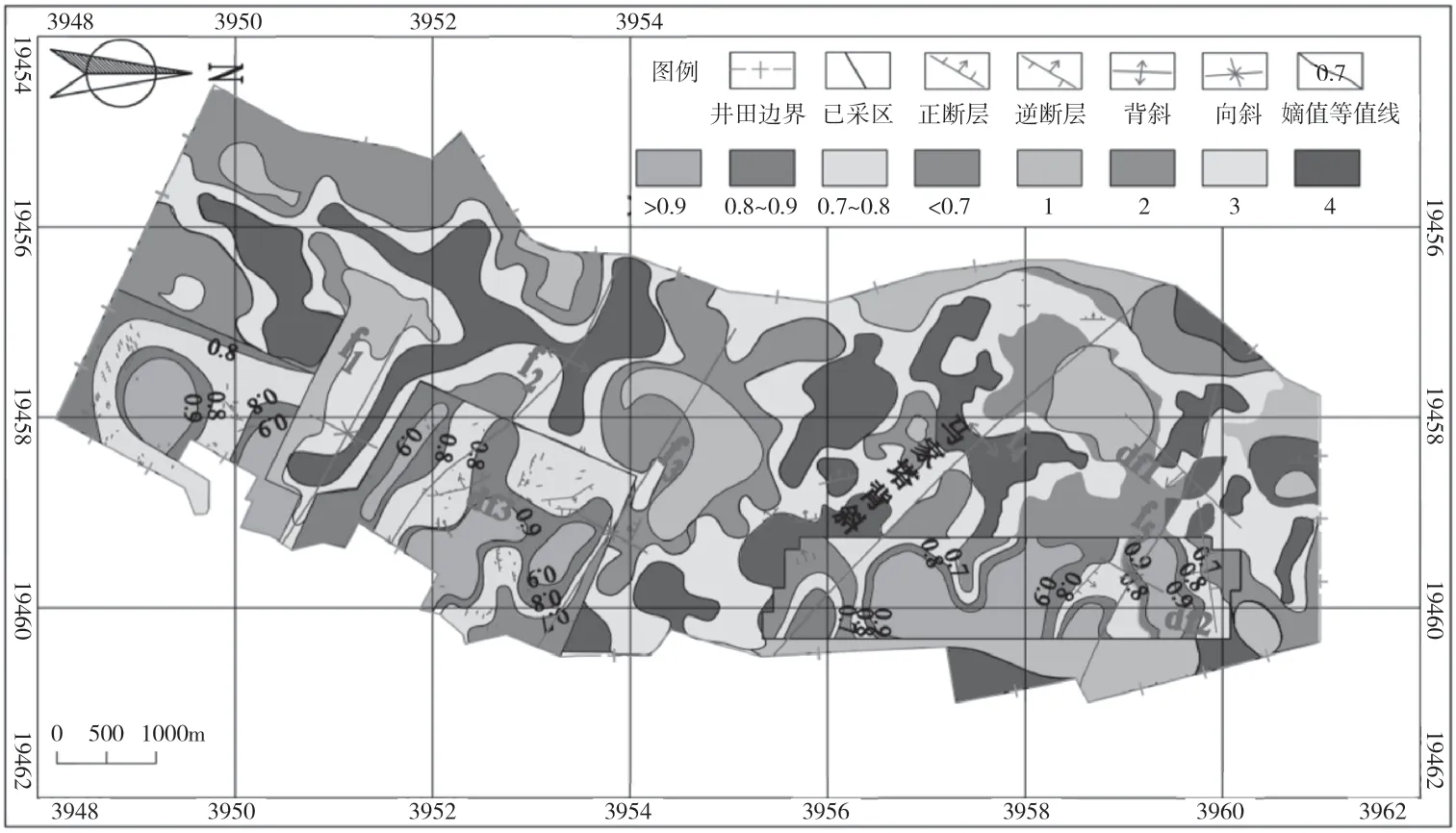
圖2 3#煤層未采區(qū)預(yù)測及已采區(qū)熵值等值線

表1 熵值計(jì)算賦值原則
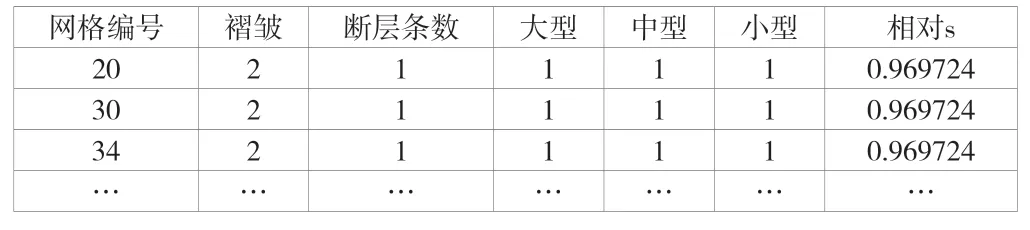
表2 3#煤層已采區(qū)相對(duì)熵值部分結(jié)果
3 未采區(qū)3#煤層復(fù)雜程度預(yù)測
基于回歸分析與模糊綜合評(píng)判相結(jié)合的方法,對(duì)該井田未采區(qū)3#煤層構(gòu)造復(fù)雜程度進(jìn)行預(yù)測,其主要步驟如下[8]:應(yīng)用回歸分析法擬選m 個(gè)評(píng)判指標(biāo),構(gòu)成評(píng)判因素集,U={U1,U2,…,Um};確定每個(gè)因素在評(píng)價(jià)過程中相應(yīng)的權(quán)重系數(shù),構(gòu)成因素集U上的權(quán)重集:A={a1,a2,…,an},=1;確定評(píng)判對(duì)象的評(píng)語論域,構(gòu)建評(píng)語集:V={V1,V2,…,Vn};建立各評(píng)語論域里的隸屬度函數(shù),R=(fjk)m×n;選擇恰當(dāng)?shù)哪:铣伤阕樱M(jìn)行模糊運(yùn)算:S=A·R;按照最大隸屬度原則,得到模糊綜合評(píng)判結(jié)果。
3.1 回歸分析篩選評(píng)價(jià)指標(biāo)評(píng)價(jià)
指標(biāo)的選取直接關(guān)系到未采區(qū)構(gòu)造復(fù)雜程度預(yù)測的精準(zhǔn)程度,然而未采區(qū)構(gòu)造發(fā)育尚未查明,因此以已采區(qū)資料為基礎(chǔ),通過回歸分析法,從擬選的影響構(gòu)造復(fù)雜程度8 個(gè)因素中(煤層厚度di、煤層厚度變異系數(shù)Vi、上覆砂巖厚度(50m 內(nèi))Zi、上覆砂巖變異系數(shù)γi、煤層底板標(biāo)高Hi、煤層底板標(biāo)高變異系數(shù)ξi、頂板巖性Qi和等高線條數(shù)Ni)篩選出與相對(duì)熵值Si相關(guān)性較高的4 個(gè)變量,合理地建立未采區(qū)評(píng)語集,同時(shí)也確立相對(duì)熵值Si回歸方程,為計(jì)算出未采區(qū)相對(duì)熵值Si提供理論基礎(chǔ)。
3.1.1 煤層厚度di(m)、煤層厚度變異系數(shù)Vi
在褶皺和斷層較為發(fā)育的地區(qū),煤層厚度變化較大,會(huì)出現(xiàn)增厚、變薄、尖滅等現(xiàn)象,對(duì)同一個(gè)礦區(qū)來講地質(zhì)構(gòu)造對(duì)煤層厚度變化影響的基本規(guī)律不變,因此可以根據(jù)已采區(qū)煤層厚度變化來推測未開采區(qū)域的構(gòu)造特征。煤層變異系數(shù)Vi 是衡量資料中煤層厚度離散程度的一個(gè)統(tǒng)計(jì)量,客觀反映了煤層厚度變化規(guī)律,消除了不同度量單位對(duì)多個(gè)因素變異程度比較的影響,如公式(3)和公式(4)所示。
式中:di為第i個(gè)網(wǎng)格單元煤層厚度;d為煤層平均厚度;n為統(tǒng)計(jì)點(diǎn)數(shù)。
3.1.2 上覆砂巖厚度(50 m 內(nèi))Zi(m)、上覆砂巖變異系數(shù)ηi
3#煤層形成于山西組第一個(gè)旋回時(shí)期,砂巖地層上覆于3#煤層頂板。在構(gòu)造復(fù)雜地區(qū)局部發(fā)育有砂巖陷落空洞,導(dǎo)致上覆砂巖厚度發(fā)生變化。可以采用上覆砂巖厚度(50 m 內(nèi))反映該地區(qū)的構(gòu)造復(fù)雜性。上覆砂巖變異系數(shù)類與煤層厚度變異系數(shù)相同。
3.1.3 煤層底板標(biāo)高Hi(m)、煤層底板標(biāo)高變異系數(shù)ξi
研究發(fā)現(xiàn)在構(gòu)造復(fù)雜區(qū),會(huì)出現(xiàn)煤層底板標(biāo)高突變的現(xiàn)象[8]。一般在褶皺地區(qū),下伏含煤地層的底板標(biāo)高會(huì)隨褶皺形態(tài)發(fā)生改變,在斷裂構(gòu)造發(fā)育區(qū)域,因斷層的兩盤發(fā)生錯(cuò)動(dòng),使兩盤中的含煤地層發(fā)生錯(cuò)位,導(dǎo)致底板標(biāo)高發(fā)生變化。其中煤層底板標(biāo)高變異系數(shù)類同于煤層厚度變異系數(shù)。
3.1.4 頂板巖性Qi
頂板巖性往往會(huì)影響構(gòu)造發(fā)育的類型,如脆性巖體受構(gòu)造應(yīng)力作用,易產(chǎn)生斷裂,形成斷層,而塑性巖體,易發(fā)生彎曲變形,形成褶曲。根據(jù)3#煤層頂板巖性的類型,分別賦予頂板巖性相應(yīng)的量化數(shù)值,見表3[6]。
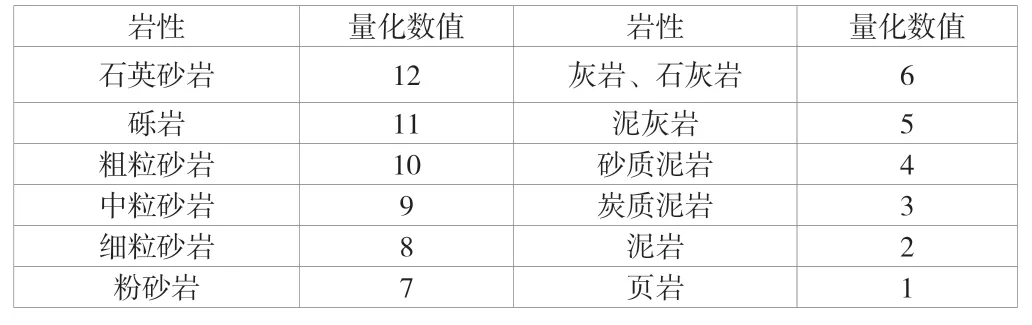
表3 3#煤層頂板巖性量化數(shù)值統(tǒng)計(jì)表
3.1.5 等高線條數(shù)Ni
研究發(fā)現(xiàn)褶皺的形態(tài)會(huì)影響研究區(qū)域的地形變化,而網(wǎng)格單元中等高線條數(shù)反應(yīng)了該地區(qū)地形變化情況,因此擬選等高線條數(shù)為影響因素之一。
3.1.6 多元回歸分析
基于SPSS 軟件多元回歸分析功能,以已采區(qū)相對(duì)熵為因變量,上述8 個(gè)因素為自變量,篩選了與相對(duì)熵值相關(guān)性較高的4 個(gè)變量,從而建立未采區(qū)評(píng)語集。SPSS 數(shù)據(jù)導(dǎo)入、處理過程及結(jié)果見表4。
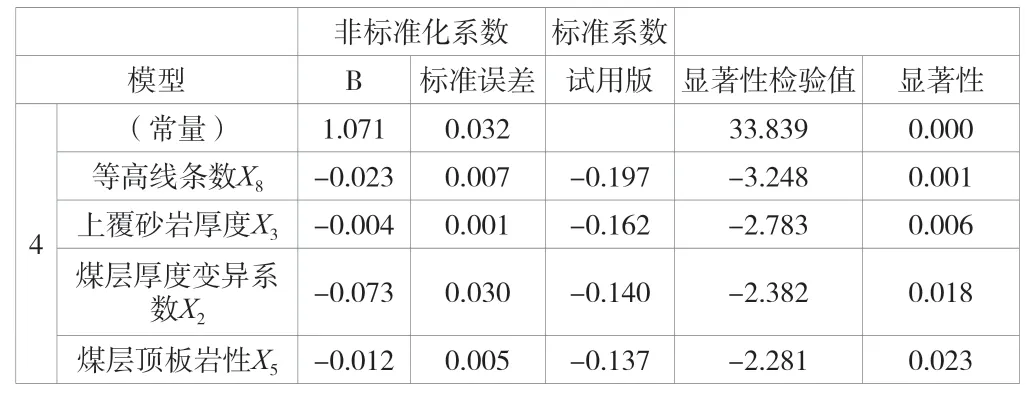
表4 模型4 回歸系數(shù)
通過回歸分析,建立相對(duì)熵值線性方程,為未采區(qū)熵值計(jì)算提供科學(xué)依據(jù),同時(shí)篩選了與相對(duì)熵值Si相關(guān)性較高的4個(gè)影響因素,最終確立了評(píng)語集:U=(Si,Ni,Zi,Vi,Qi)。
3.2 評(píng)語等級(jí)劃分標(biāo)準(zhǔn)
基于《煤礦地質(zhì)工作規(guī)定》有關(guān)地質(zhì)構(gòu)造的4 類劃分法,確定評(píng)語等級(jí)標(biāo)準(zhǔn),將3#煤層未采區(qū)構(gòu)造復(fù)雜程度劃分為4種等級(jí),V={V1,V2,V3,V4},V1簡單,V2中等,V3較復(fù)雜,V4復(fù)雜。根據(jù)數(shù)理統(tǒng)計(jì)方法,并結(jié)合井田地質(zhì)特點(diǎn),得到各評(píng)價(jià)指標(biāo)造復(fù)雜程度分類標(biāo)準(zhǔn),見表5。
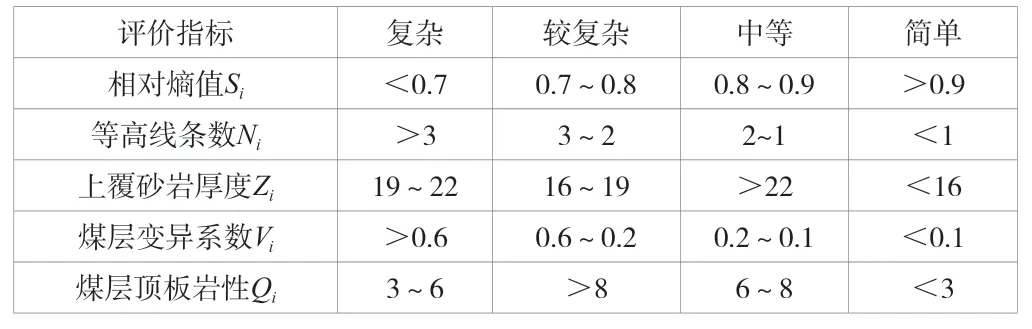
表5 3#煤層各評(píng)價(jià)指標(biāo)造復(fù)雜程度分類標(biāo)準(zhǔn)
3.3 權(quán)重
權(quán)重是決定評(píng)價(jià)指標(biāo)對(duì)評(píng)價(jià)結(jié)果影響的主要因素,利用灰色關(guān)聯(lián)的分析法確定各個(gè)評(píng)價(jià)指標(biāo)的權(quán)重值。在各評(píng)價(jià)指標(biāo)中,相對(duì)熵值Si綜合反應(yīng)了構(gòu)造復(fù)雜程度,因此以相對(duì)熵值Si為參考數(shù)據(jù)列,其他4 個(gè)評(píng)價(jià)指標(biāo)作為比較數(shù)據(jù)列,再進(jìn)行權(quán)重計(jì)算。具體做法:評(píng)價(jià)指標(biāo)的原始數(shù)據(jù)初始化、均值化處理→各比數(shù)據(jù)較列與參考數(shù)據(jù)列絕對(duì)誤差值計(jì)算→確定最大和最小絕對(duì)差值→關(guān)聯(lián)系數(shù)和關(guān)聯(lián)度計(jì)算→歸一化處理→得出權(quán)重系數(shù)。各評(píng)價(jià)指標(biāo)關(guān)聯(lián)度和權(quán)重系數(shù)計(jì)算結(jié)果具體見表6。
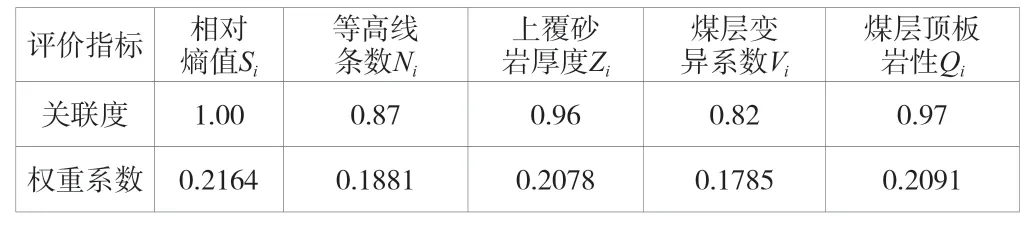
表6 評(píng)價(jià)指標(biāo)關(guān)聯(lián)度和權(quán)重系數(shù)
3.4 隸屬度函數(shù)
結(jié)合表5 構(gòu)造復(fù)雜程度與各個(gè)影響因素之間的關(guān)系,3#煤層采用“降半梯形”建立隸屬度函數(shù)結(jié)果如下[1,5],以等高線為例構(gòu)造隸屬度函數(shù),構(gòu)造簡單(f11(x))、構(gòu)造中等(f12(x))、構(gòu)造較復(fù)雜(f13(x))、構(gòu)造復(fù)雜(f14(x))的函數(shù)具體形式如公式(5)所示。
3.5 模糊運(yùn)算
某網(wǎng)格單元關(guān)于構(gòu)造復(fù)雜程度等級(jí)j的聚類系數(shù)如公式(6)所示。
式中:fij(x)為單元格第i個(gè)參數(shù)屬于第j類的函數(shù);ηi為單元格第i個(gè)參數(shù)的權(quán)重值;σij為網(wǎng)絡(luò)單元格聚類系數(shù)。
通過計(jì)算網(wǎng)格單元的聚類系數(shù),得到每個(gè)單元格的構(gòu)造復(fù)雜程度隸屬度。根據(jù)網(wǎng)絡(luò)單元的4 個(gè)評(píng)語集別的隸屬度關(guān)系確定網(wǎng)格單元的構(gòu)造復(fù)雜程度級(jí)別。遵循最大隸屬度原則,確定網(wǎng)格單元最終評(píng)價(jià)結(jié)果。根據(jù)評(píng)價(jià)結(jié)果繪制出3#煤層未采區(qū)構(gòu)造復(fù)雜程度預(yù)測結(jié)果圖,并統(tǒng)計(jì)出各個(gè)預(yù)測等級(jí)所占的百分比。
3.6 未采區(qū)3#煤層預(yù)測
根據(jù)圖2 和表7 可知,較復(fù)雜及復(fù)雜區(qū)塊占未采區(qū)的67.61%,所處位置主要集中在已采區(qū)3#煤層的中南部、北部區(qū)域及f1向斜、f2背斜、f4背斜、f5向斜所在區(qū)域。基本簡單、中等的區(qū)塊分布雜亂,主要集中在中部、南部少數(shù)區(qū)域及北部邊緣地帶。

表7 未采區(qū) 3#煤層構(gòu)造等級(jí)百分比
4 結(jié)論
3#煤層整體分析表明復(fù)雜區(qū)塊主要集中在北區(qū)df1斷裂構(gòu)造區(qū)域、中區(qū)f4背斜區(qū)域、南區(qū)f1向斜與f2背斜之間區(qū)域。其中,已采區(qū)相對(duì)熵值小于0.7 的構(gòu)造復(fù)雜區(qū)塊主要分布在南區(qū)、中區(qū)局部區(qū)域內(nèi)。未采區(qū)構(gòu)造復(fù)雜區(qū)塊主要集中在中南部、北部區(qū)域及f1向斜、f2背斜、f4背斜、f5向斜所在區(qū)域,簡單、中等的區(qū)塊分布雜亂,主要集中在中部、南部少數(shù)區(qū)域及北部邊緣地帶。
3#煤層未采預(yù)測結(jié)果與實(shí)際鉆孔揭露情況吻合度較高,預(yù)測結(jié)果明確了各構(gòu)造等級(jí)的分布區(qū)域,為煤礦生產(chǎn)部署提供一定參數(shù)。

