基于層次聚類的橋梁模態參數自動識別及異常診斷

馬新穎

(天津城建設計院有限公司,天津 300122)

橋梁運營模態參數一般通過分析健康監測系統加速度數據獲得,大量長期的模態參數是評估橋梁-環境相關性和結構整體性能演化過程的重要基礎[2]。傳統橋梁監測的加速度數據的分析依靠商業模態分析軟件,但是商業軟件每次只能分析一次數據,得到一組模態參數。為了獲得大量模態參數,模態參數自動識別方法逐漸得到重視,研究最多的是基于穩定圖識別的模態參數自動識別[3-6]。

許多研究人員將聚類算法引入穩定圖自動識別,如譜系聚類[5]、圖論聚類[4]、模糊聚類和層次聚類[3]等,其中譜系聚類、圖論聚類和層次聚類雖然從聚類方法屬于不同的方法分支,但從識別過程上來說,具有相同的原理,都學要設定合適的閾值來實現聚類,而現有方法基本都采用固定閾值[5,6]。固定閾值通常基于經驗獲得,實際情況中,不同的結構需要不同的閾值,因此,固定閾值識別得到的模態參數通常不是很準確,要想得到精確的模態參數,必須尋求其它方法。

為解決現有模態參數識別結果的精度問題,本文提出基于兩階段層次聚類的模態參數自動識別及基于箱形圖的異常值診斷方法。通過對原始層次聚類方法進行改進,分頻率和振型兩階段分別進行聚類,識別穩定軸;然后將基于箱形圖的異常值檢測算法引入模態參數識別,檢測穩定軸數據中的異常值,剔除異常值,得到精確的模態參數識別結果。

1 基本理論

1.1 層次聚類

層次聚類算法主要用在大數據分析和圖像識別領域,層次聚類是基于某項指標對待分析數據按照相似性歸類的過程,將小于指標的數人為具有相似性,歸為一類,否則單獨成一類。層次聚類首先假定數據集中的每一個數據都是一個小類,計算每個小類之間的距離,形成距離矩陣;然后將距離小于聚類指標的數據合并成一類,形成新類;最后再計算每個新類之間的距離,將距離小于聚類指標的類再合并成一類。按上述過程不斷循環,直至所有類之間的距離大于聚類指標,則停止聚類,得到最終聚類結果。

為反應樣本整體數據特性,本文采用每個類的平均值之間的間距作為類間距離。

1.2 基于箱形圖的異常值檢測

箱形圖于1977年由美國著名統計學家約翰·圖基首先提出,是一種用來顯示數據分散情況的統計圖,通過箱形圖能夠顯示待統計數據的最大值、最小值、中位數、及上下四分位數,可以分析數據長期變化及多組數據的不同。箱形圖的分位數的計算完全基于樣本數據本身,不依賴任何數據特征的假設,因此箱形圖的分位數能夠反映樣本本身的固有數據特征。

基于箱形圖的異常檢測指一組數據中小于Q1-1.5IQR或大于Q3+1.5IQR的值,其中Q1表示上四分位,Q3表示下四分位,IQR表示四分位間距。基于箱形圖的異常值檢測從已有數據的本身特性出發,不對樣本數據進行任何分布假設,因此能夠最合理的識別異常值。

基于箱形圖的異常值檢測方法相比于其他異常值檢測方法具有更好的耐抗性,該方法以樣本數據的四分位數和四分位距為指標,而四分位數具有較強的抗噪性,即使含噪樣本有多個異常值也不會很大的擾動樣本的四分位數,所以異常值不能對這個標準施加影響,箱形圖識別異常值的結果比較客觀。

2 基于兩階段層次聚類的模態參數自動識別及異常診斷

2.1 兩階段的層次聚類法

聚類過程實際上是具有相似特征的數據的歸類過程,通過設定歸類指標,將小于該指標的數據歸為一類。

在穩定圖理論中,穩定軸的基本判別指標是識別結果的連續性,在識別結果的所有物理指標中,頻率的穩定性占首要位置。傳統聚類算法將頻率和MAC的聚類指標強行合并,容易將非穩定點識別為穩定點,由此造成識別結果不準確。

為了避免將非穩定點識別為穩定點,對傳統聚類算法進行改進。首先基于層次聚類算法,以頻率差為聚類指標,將頻率穩定點進行聚類,識別頻率穩定軸,并剔除穩定點較少的軸,頻率穩定點較少說明在頻率上不穩定,頻率不穩定的點一定是虛假識別結果;然后,再次運用層次聚類法,以MAC值為聚類指標,將識別的頻率穩定軸中的識別結果按MAC指標進行聚類,并剔除MAC穩定點較少的類,保留穩定點較大的類作為最終識別結果。

兩階段聚類過程分別在聚類的兩個階段將頻率和MAC作為聚類參數指標,有效克服了傳統聚類算法可能將非穩定點納入穩定軸的缺點。

2.2 迭代的箱形圖異常值診斷

穩定圖中不同階的穩定軸具有不同的數據離散特性,現有聚類算法(包括本文方法)都采用固定的聚類指標進行穩定軸識別,這種根據工程經驗確定的聚類指標一般都偏大,導致識別結果中存在一些異常值。

為準確評估識別結果的合理性,剔除識別結果中的離散值,識別得到更準確的模態參數,引入基于箱形圖異常值診斷方法的迭代的異常值剔除過程,通過對識別的穩定軸中的頻率、MAC及阻尼比等指標進行異常檢測,剔除異常識別結果,得到最終穩定軸識別結果。傳統采用頻率和MAC聯合指標的聚類過程得到穩定軸后無法判別阻尼比等物理參數的合理性,因此很容易引入阻尼比異常的識別結果,提出的箱形圖異常值檢測方法能夠檢測識別結果中任何物理指標的合理性,保證識別結果的精確性。

基于箱形圖的迭代的異常值診斷過程如下。

(1)首先計算識別結果中的某物理參數的箱形圖分位值,并計算異常值診斷指標。

(2)然后,剔除位于箱形圖之外的異常數據。

(3)最后,以剩余的識別結果為樣本,重復(1)(2),直至沒有異常值被檢測出,停止計算。

2.3 基于兩階段層次聚類的模態參數自動識別及異常值診斷流程

通過對聚類過程的改進,并引入基于箱形圖的異常值診斷過程,實現穩定軸自動精確識別。

3 工程實例

3.1 橋梁概況

橋梁為576.2+1418+481.8=2 476(m)的雙塔三跨連續鋼箱梁懸索橋,大橋建成之初便安裝了健康監測系統,其中主梁共安裝26個豎向傳感器,上下游對稱布置。本文采用2014年11月1日零時的監測數據進行分析,驗證所提算法的合理性。

3.2 模態參數識別

基于SSI法識別模態參數,系統階次設定為2～100。識別得到的所有模態參數如圖1。從圖1上雖然能夠看到穩定軸,但也存在大量的非穩定點。

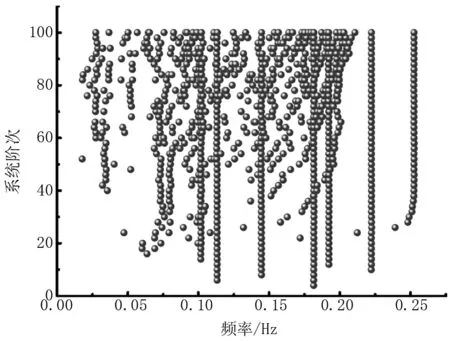
圖1 全部識別結果

3.3 基于兩階段層次聚類的穩定軸自動識別

將聚類指標設為頻率差1%,MAC差2%,分兩階段對識別結果進行聚類分析,將穩定點數量小于20的軸視為虛假軸并剔除。圖2和圖3分別表示第一階段基于頻率的穩定軸識別結果和第二階段基于MAC的識別結果。

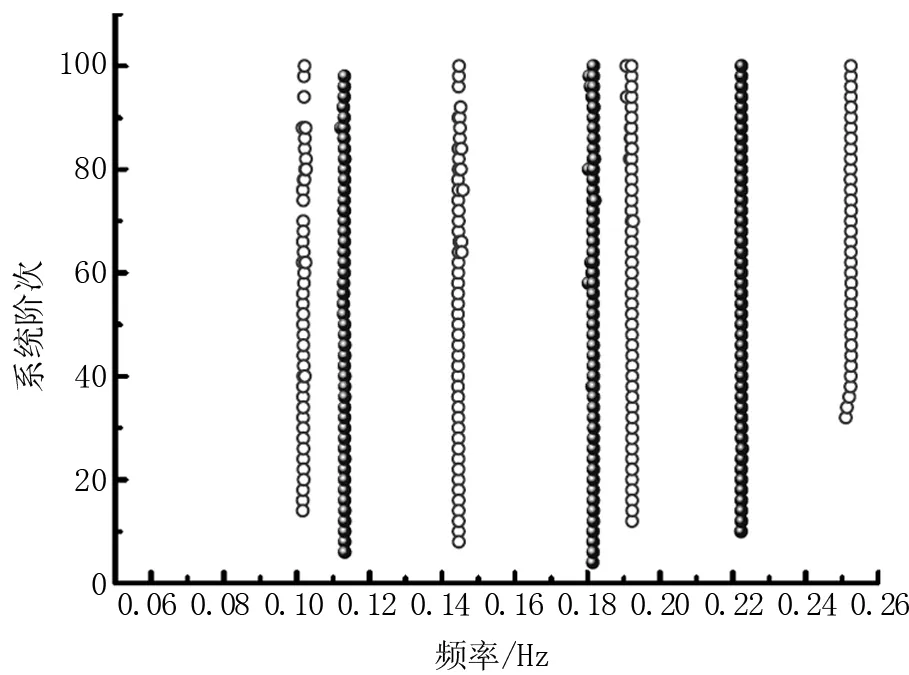
圖2 一階段基于頻率的識別結果

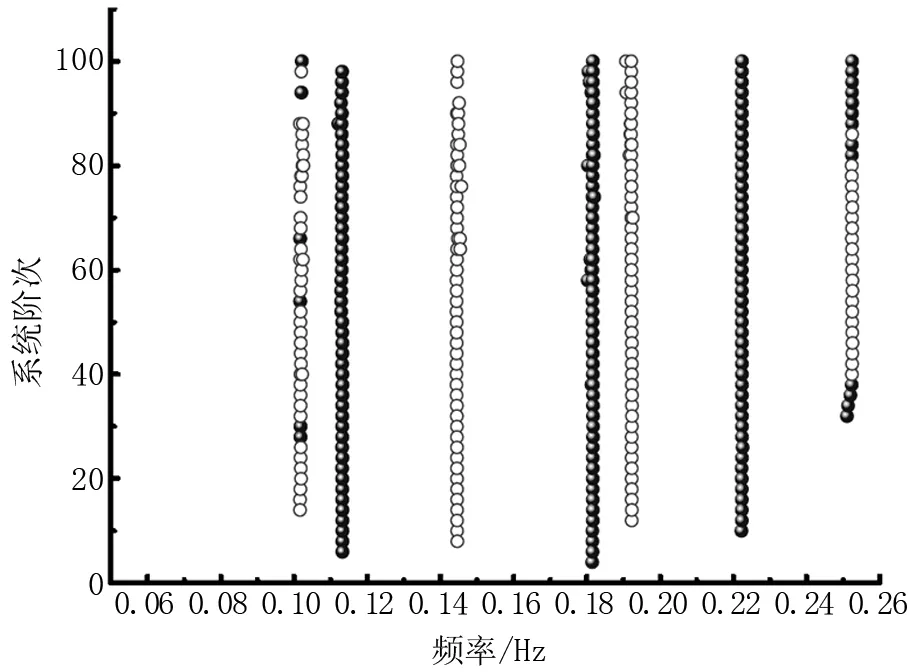
圖3 二階段基于MAC的識別結果

從圖2可以看到,第一階段基于頻率的穩定軸自動識別過程準確識別得到穩定軸,并剔除了其他虛假模態軸,第一階段的聚類過程只以頻率作為聚類指標,因此穩定軸在穩定圖上相對連續。

從圖3可以看到,基于MAC的二次聚類過程將第一階段識別的穩定軸中的第一階和第七階穩定軸又劃分成多個類,這說明,第一階段基于頻率的聚類過程識別得到的第一和第七階頻率穩定軸在振型上并不連續,存在振型識別結果異常點。第二～第六階識別結果沒有出現MAC異常點,說明第二～第六階識別結果在頻率和振型上都比較穩定。將第一和第七階識別結果中振型不穩定點剔除將第二階段聚類得到的每一類中數據量較少的類剔除,剩余的結果即聚類識別得到的穩定軸。

3.4 迭代的箱形圖異常值檢測

將兩階段聚類得到的穩定軸內的數據進行箱形圖異常值檢測。圖4、圖5、圖6分別表示對一階頻率、一階振型MAC和一階阻尼比的箱形圖檢測結果。

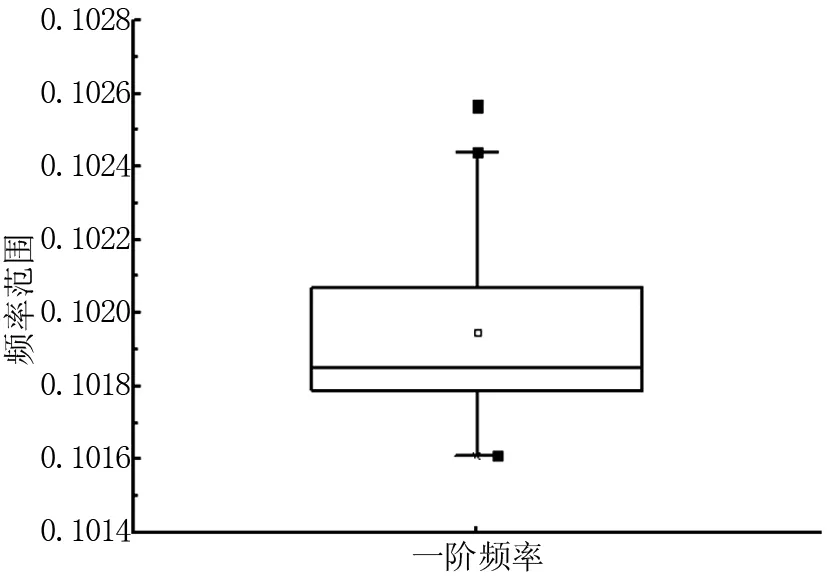
圖4 一階頻率異常值檢測

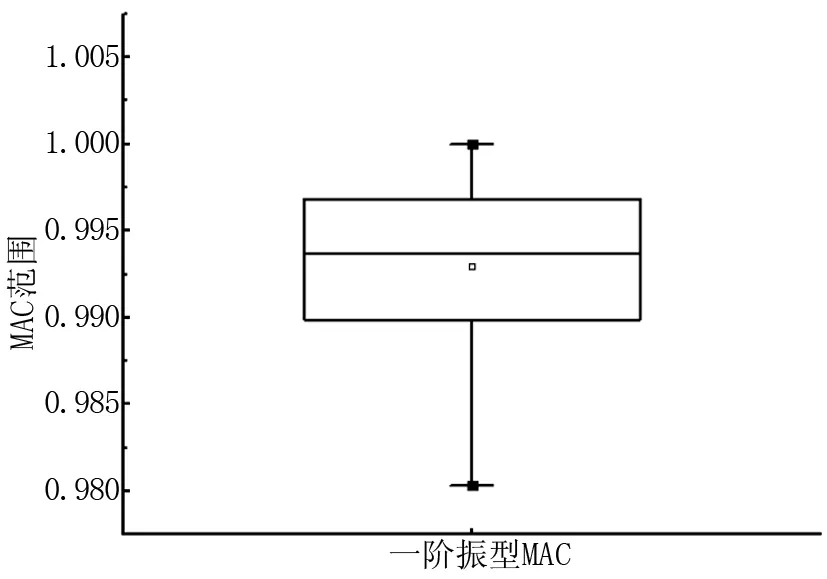
圖5 一階振型MAC異常值檢測

圖6 一階阻尼比異常值檢測

從圖4可以看到,盡管兩階段聚類過程識別得到頻率和振型都穩定的穩定軸,但是頻率仍然存在異常值,說明針對背景橋梁,基于經驗確定的頻率聚類指標偏大。圖5表明振型MAC值沒有出現異常值,說明基于經驗選取的MAC聚類指標合理。圖6結果表明一階阻尼比識別得到較多的異常值,說明僅僅依靠頻率和振型MAC指標的聚類結果不能得到合理的阻尼比識別結果。篇幅限制,其它階穩定軸識別結果不再列出。

采用迭代的異常值剔除過程,對一階識別結果進行異常值剔除,頻率經過4次異常值剔除后不能檢測到異常值,得到最終識別結果。振型由于原本不存在異常值,所以只進行對應的刪除過程。識別阻尼比經過6次異常值剔除得到最終識別結果,在對頻率和阻尼比剔除的過程中,同時剔除對應的其它識別結果。

以上過程說明,兩階段的聚類過程和基于箱形圖的異常值診斷能夠實現穩定軸自動識別,相較于原始聚類算法,能識別得到更準確的聚類結果。

4 結 論

(1)基于頻率的聚類方法能夠自動識別得到穩定軸,但識別結果中包含振型非穩定點。

(2)基于MAC的二次聚類過程能夠剔除頻率穩定軸中的振型非穩定點,得到頻率和振型都穩定的識別結果。

(3)基于箱形圖的異常值診斷方法識別得到較多的阻尼比異常值,解決傳統聚類算法不能判別阻尼比識別結果可靠性的缺點。

(4)基于箱形圖的異常值檢測方法能夠識別并剔除穩定軸中的異常值,提高基于固定指標的聚類結果的識別精度。