考慮車輛交互信息的高速匝道合流區車輛加減速行為研究

車 鑫

(重慶交通大學,重慶 400074)

0 引 言

匝道合流區作為匝道車輛與主路車輛交匯的區域,在匝道車輛進行強制換道操作時容易出現交通流紊亂的現象,Kondyli[1]等人得出的研究表明,匝道影響區從匝道鼻端上游120 m處開始并于鼻端下游260 m處結束,而這種現象的出現會影響交通效率并帶來安全性問題。因此該區域一直是學者及相關技術人士研究的重點。張鑫[2]等以效率-交通沖突率作為評價指標,分析了加速車道幾何參數對合流區交通環境的影響;李巧茹[3]等提出了基于可變限速和換道控制的合流區協同控制模型;Kusuma[4]等人發現91%的臨近匝道車道行駛的駕駛員會在加速車道前方進行減速,且48%的匝道合流車輛會在前25%的交通區段進行換道操作;Beinum[5]等研究了匝道合流區的駕駛行為。以上文獻從人、車、路、環境四個角度對合流區交通環境進行了分析與改善。然而當前的文獻資料,大多集中在匝道車輛合流行為及區域交通效率提升等方面,討論主路及匝道車輛間微觀交通參數與車輛加減速行為關系的資料相對較少。而在匝道合流區,車輛交互行為(如車輛換道)會比其它路段更多,當保持多車跟馳狀態或匝道來車時,駕駛員可能會出現無法正確判斷前方車輛運行狀態的情況,從而提高車輛運行風險并降低通行效率。而車輛周圍環境的變化往往會影響駕駛人的意圖,進而影響駕駛員之后的決策行為,所以通過車輛交互信息來預判前車運行狀態很有必要。在信息技術不斷發展的今天,隨著路端設備或車載傳感器的部署,我們可以很容易的獲取到這些車輛的自身信息與交互信息,使預判前方車輛行駛狀態成為可能。因此本文討論了速度、車輛間距、速度差等微觀運行參數與車輛加減速行為的關系,并借助以上參數利用聚類分析的方式預判車輛未來短期的運行狀態。

1 各場景下影響車加減速行為的主要因素

1.1 數據集的選取與處理

本次研究選取了清華大學蘇州汽車研究院提供的Mirror-Traffic數據集,該數據集記錄了某市高速公路匯入路口的車輛軌跡數據,記錄時長為30 min。該數據集包含760輛車共計14.3萬余條數據。數據的采樣幀率為25 Hz,包含車輛編號、位置、速度、加速度等車輛運行信息。數據集所選區域為雙向四車道的匝道合流區,匝道連接方式為平行式,限速80 km/h。在下面的研究中,將遠離匝道一側的主路記作主路一,靠近匝道一側的主路記為主路二,合流區示意圖如圖1所示。

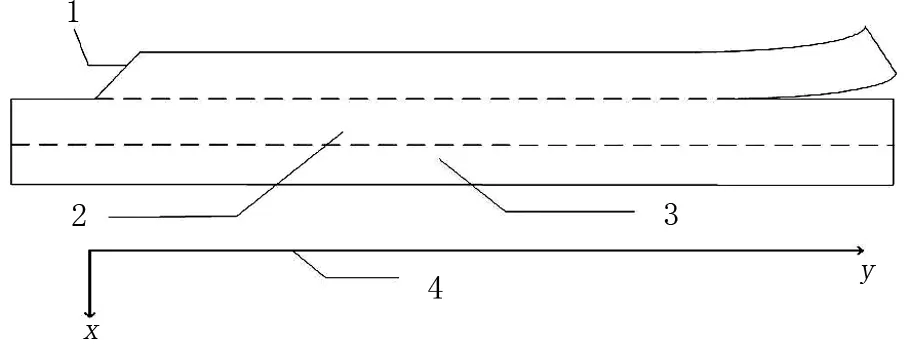
1—加速車道;2—主路二車道;3—主路一車道;4—x-y坐標軸:車輛點位坐標(x,y)對應的基準坐標軸。圖1 平行式匝道合流區示意圖

在分析數據前需對其進行簡單處理。首先處理匝道車輛數據,匝道車輛軌跡圖如圖2所示?？梢钥吹?匝道車輛最早在縱向點位y=160 m處左右開始出現平行于主路車道的軌跡,因此匝道合流車輛僅采集縱向點位前160 m處的車輛數據;在提取車輛間距信息時,兩車縱向間距最大值設置為70 m,同時由于加速度數據波動較大,所以對其進行了卡爾曼濾波處理。

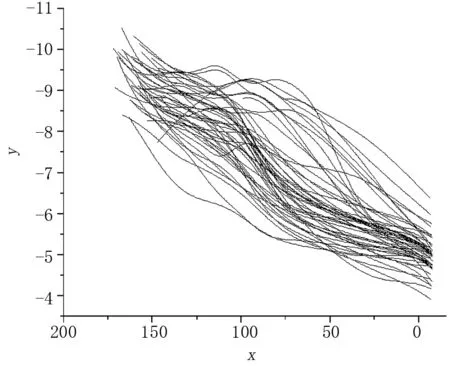
注:將每輛車在各采樣點位的坐標(x,y)按采樣時間順序進行連接,形成匝道車輛行駛軌跡。圖2 匝道車輛行駛軌跡圖(單位:m)

1.2 各場景間的差異性分析

由于車輛的運行特性受所在車道、匝道是否有來車等因素影響,所以將合流區分為六個場景,分別為匝道來車時,主路一與主路二車輛運行場景、匝道無來車時,主路一與主路二車輛運行場景以及加速車道車輛行駛時,斜前方與斜后方(位于主路二)有車的場景。為敘述方便,將上述場景以此記為場景一到場景六。其中場景一到場景四所選的參數為自車速度、前后兩車間的速度差、縱向間距、車頭時距,場景五和場景六所選參數為自車速度、速度差、橫向及縱向間距。以上所選參數經驗證均服從正態分布。

為了驗證各個場景間的差異性,這里采用獨立樣本t檢驗的方法來判斷。由于各樣本間的數量級不一致,會影響獨立樣本t檢驗得出的結論,故利用smote過采樣算法將各個樣本擴容。擴容后利用SPSS軟件求出的相應結果如表1、表2所示。盡管場景一和場景二、場景三和場景四之間各有一個參數差異性不顯著,但場景間其他三個參數均存在明顯的差異,因此從整體上看六個場景間存在差異。接下來研究各場景對應的參數與車輛運行狀態即車輛加速度之間的關系。

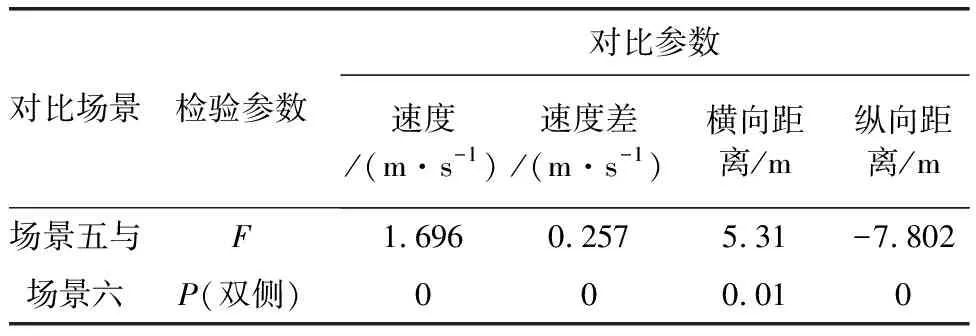
表2 匝道場景差異性分析

1.3 車輛微觀交通參數與車輛運行狀態間的關系

為研究各參數與車量加速度間的關系,采用皮爾遜相關系數r來判別二者的相關性

(1)

式中:x、y為需要判別相關性的兩個樣本,Cov(x,y)為x與y的協方差;Var(x)、Var(y)分別為x與y的方差。

各場景參數與加速度的相關系數如表3、表4所示。

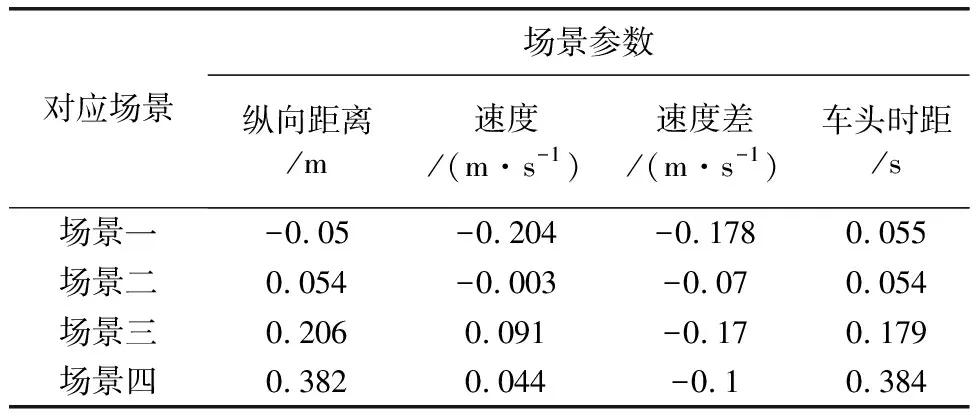
表3 各主路場景參數與加速度的相關系數

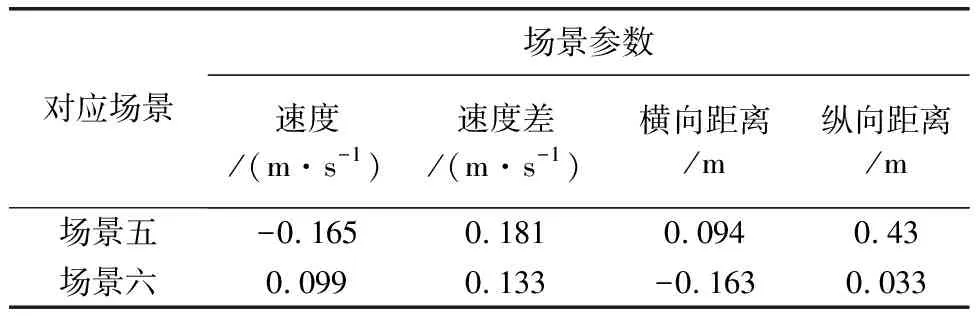
表4 各匝道場景參數與加速度的相關系數

分析包含兩條主路的場景,可以看到不同場景的參數與加速度的相關程度是存在差異的,這里以場景一和場景四為例,場景一中速度和速度差與加速度相關性高,而場景四中縱向距離與車頭時距與加速度相關性高。同時也可以發現不同場景下各參數與加速度的正負相關性、相關的的顯著性也存在著部分差異,這也側面驗證了場景之間的差異性。再分析另外兩個場景,可以看到,場景五的整體相關性水平、相關的顯著性均強于場景六,說明加速車道車輛行駛狀態受前方車輛影響更大。

根據相關性分析結果,選取相關性最強的系數所對應的場景作為案例進行聚類分析,因此這里以場景四和場景五作為案例進行分析。

2 車輛運行狀態聚類方法研究

在常規聚類方法中k-means算法憑借著其操作簡單,收斂速度快而備受廣大研究者青睞,如張建波[6]等利用k-means算法分析了駕駛員的急減速特征;蘇小會[7]等利用了改進的k-means算法對車輛油耗進行了分析。但由于k-means方法偏向于對球形簇進行聚類,再加上簇之間容易發生交疊現象,聚類結果在有些情況下可能會不盡人意。而高斯混合模型(GMM)作為K-means模型的優化,它可以試圖找到多維高斯模型概率分布的混合表示,從而擬合出任意形狀的數據分布,而該模型也廣泛地運用在聚類方法的研究中,吳堅[8]等基于高斯混合模型對駕駛員的特征進行了辨識;張建波[9]等利用該模型對不同交通條件下的駕駛員進行了特征聚類。由于樣本數據服從高斯分布,符合GMM的應用條件,因此這里可以選擇GMM聚類的方法對車輛運行狀態進行分類。在這里,將車輛的運行狀態分為加速態、平穩行駛態、減速態三類,并對K-means和GMM兩種聚類算法的效果進行了對比。

2.1 GMM與k-means算法的基本原理

k-means算法是通過在確定k個聚類個數的情況下隨機確立k個聚類中心,分別計算第i個樣本點到各個聚類中心的距離rij

rij=‖xi-μj‖2(j=1,2,…,kandi=1,2,…,N)

(2)

式中:xi為第i個樣本點,μj為第j個聚類中心,k為聚類中心個數,N為聚類樣本總個數。

GMM算法則通過多個正態分布的加權和來表示一個隨機變量的概率分布,其對應的高斯混合分布可表示為

(0≤ωi≤1)

(3)

式中:m為高斯函數混合個數;ωi為混合系數;μi為第i個高斯混合分布的均值;σi為第i個高斯混合分布的標準差。

而利用GMM聚類過程即先劃分k個聚類簇,之后利用包含多元參數的訓練集來訓練該模型,形成k種不同的多元高斯分布圖(簇),最后將需要聚類的樣本(測試集)導入訓練好的模型,求出該樣本在k個不同分布圖中的概率,選取概率最大的簇作為結果進行輸出。

在樣本訓練的過程中,首先對混合系數αi,均值向量μi以及協方差矩陣∑i進行初始化,之后利用隱變量確定樣本來源于某一類,接下來計算該類中產生該樣本的概率,從而求出對應的對數似然函數

(4)

式中:PM(xj)為樣本xj的后驗概率;m為樣本個數;k為聚類簇個數;αi為混合系數;μi與∑i分別為對應的均值向量與協方差矩陣。

2.2 車輛運行狀態的聚類分析

聚類分析前需要對聚類參數進行合理的選取,這里以參數與加速度的相關性和聚類參數之間的相關性兩個方面進行評判。在場景四中,由于車輛間距與車頭時距兩個參數間的相關系數高達0.918,因此利用表3得出的結論選取車頭時距與速度差作為聚類參數;在場景五中,各參數間相關性并不高,所以根據表4得出的結果選取速度差、縱向間距、速度作為聚類參數。

為了更好地展現聚類效果,需對上述兩種場景的樣本進行降維處理,即對同一輛車,每十幀數據做一次均值,得到聚類樣本數據,之后對該樣本數據進行聚類,通過聚類結果與實際運行情況進行對比的方式來評判聚類效果,其中實際運行情況分別通過前述兩種聚類方式進行了量化分級。場景四、場景五所對應的車輛運行趨勢的k-means算法聚類結果如圖3、圖4所示,GMM算法聚類結果如圖5、圖6所示。從聚類結果來看GMM算法均優于K-means算法,但在場景四、場景五所對應的兩算法的預判正確率卻僅為52.2%,40.74%與45.2%,43.1%。其正確率較低的原因主要歸結為以下3點。

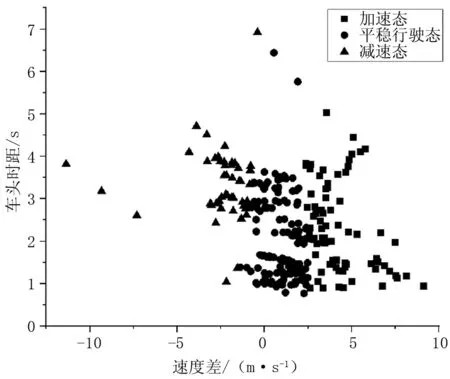
圖3 場景四車輛運行趨勢k-means算法聚類圖

圖4 場景五車輛運行趨勢k-means算法聚類圖

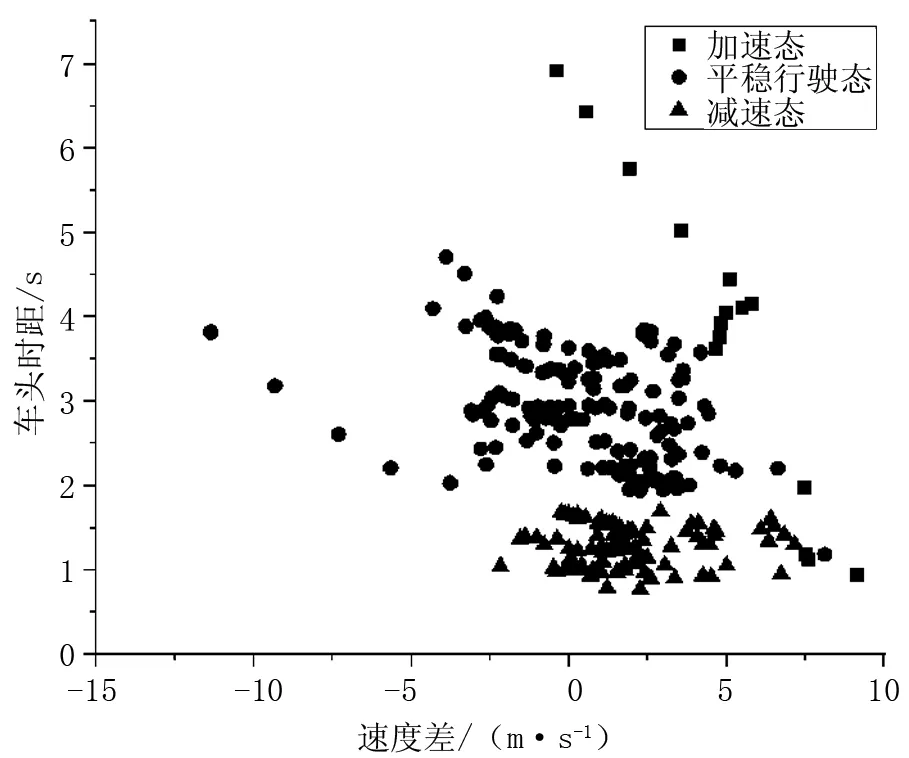
圖5 場景四車輛運行趨勢GMM算法聚類圖

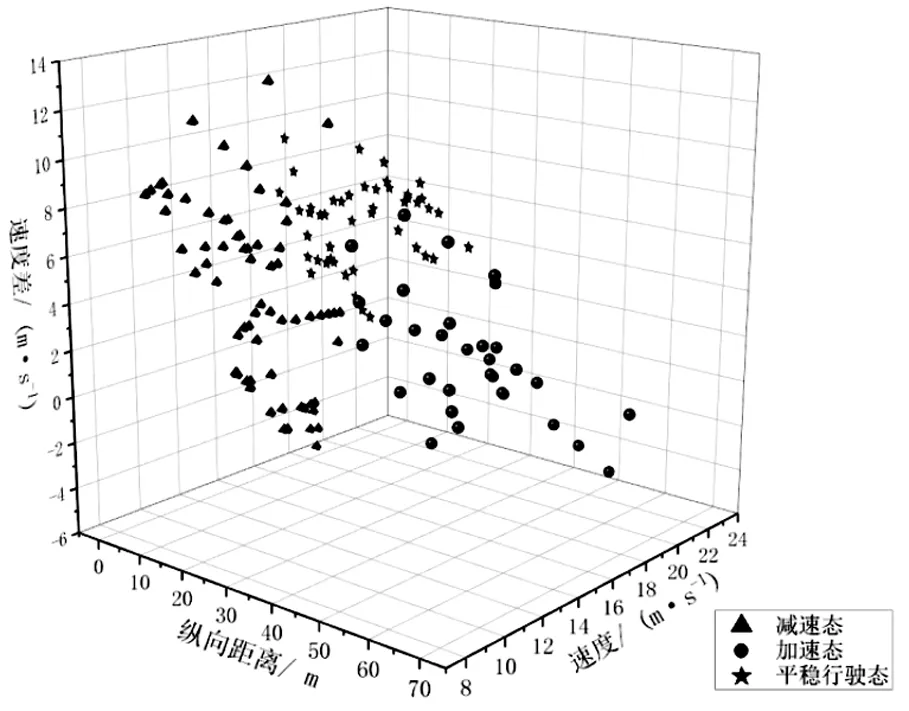
圖6 場景五車輛運行趨勢GMM算法聚類圖

(1)在該場景下微觀交通參數與加速度之間的相關性依然較低。

(2)該區域交通環境復雜,受駕駛員心理因素(駕駛風格)的影響相對于常規場景更大。比如在場景四中,就出現了在較低的車頭時距中依然有車輛加速行駛的情況。

(3)應該考慮車道占有率等相對宏觀的交通信息。

綜上所述,在該區域進行車輛運行狀態預測時應該強化對駕駛員駕駛風格的辨識,在車輛運行狀態預判時應該將駕駛風格進行量化,將其作為參數與其他相關交通參數一同作為預判依據,從而減少誤判的可能。

3 結 論

著重分析了車輛交互信息與車輛加減速行為的關系,其中靠近匝道側的主路車輛運行狀態與車頭時距、車輛間距相關性強。而匝道車輛運行狀態受臨近車道前車影響更大,與其縱向距離相關性強。根據聚類的分析結果說明僅依靠車輛交互信息及自身速度并不能完全把握車輛運行狀態,還需要考慮駕駛員自身特性等因素。本次研究所得出的結論為車輛行駛狀態預測參數的提取提供了依據。