考慮諧波電流的驅動電機振動噪聲優化
戴佳錢,曾發林,徐求福,王佳圣
(江蘇大學 汽車工程研究院, 江蘇 鎮江 212013)
0 引言
電動汽車驅動電機的振動噪聲是整車振動噪聲的主要組成部分[1]。驅動電機的振動噪聲特性與傳統內燃機有較大差別,除空氣動力噪聲與機械噪聲外,由電機永磁體磁密與電樞磁密相互作用產生的具有階次特性的徑向電磁力是引起電機殼體振動并輻射產生噪聲的主要原因[2]。通過優化電機徑向電磁力改善電機振動噪聲具有十分重要的意義。
國內外研究對電機徑向電磁力的優化方法主要涉及結構優化與電流諧波優化。文獻[3]分析總結了不同極槽配合和繞組層數電機的最低徑向力波階數,并指出力波階數小的極槽配合更易引起較大的振動。文獻[4]推導了轉子分段斜極的徑向力波解析式并通過調整分段數降低了電機的振動噪聲。然而結構優化一般在電機本體設計階段進行考慮,并且無法動態優化徑向電磁力。優化諧波電流可以針對性地調整徑向電磁力的時空分布,文獻[5]提出了一種電機電磁振動噪聲半解析模型,并分析了諧波電流對電機振動噪聲的影響,為針對諧波電流的優化提供了參考。文獻[6]分析了注入諧波電流優化徑向電磁力的原理,并推導出了永磁同步電機徑向電磁力波的諧波電流補償模型。文獻[7]基于多倍頻電流注入法的徑向振動抑制模型,設計優化算法實現了各頻次徑向振動的綜合抑制。文獻[8]針對分數槽電機中的低模數電磁力諧波,采用注入補償電流的方式降低了電機的電磁振動。文獻[9]分析指出對整數槽永磁同步電機振動噪聲影響最大的是空間0階次徑向電磁力波。文獻[10]分析了某車用永磁同步電機0階徑向電磁力波的主要來源,通過注入13次諧波電流的方法削弱了72階次噪聲。
本文以某8極48槽永磁同步驅動電機為研究對象,采用優化電機電流諧波的方式降低振動噪聲。采集電機噪聲信號并分析各階次徑向電磁力在不同轉速下對電機振動噪聲的影響,選擇3 000 r/min轉速為研究工況,使用實驗噪聲信號驗證建立的磁固聲耦合仿真模型。建立考慮電流諧波的徑向電磁力解析模型,基于實驗采樣電流分析各部分徑向電磁力時空特征。通過有限元方法仿真計算各定子齒至測點處的噪聲傳遞函數,同時采用柯特斯公式計算各部分徑向電磁力波作用于各定子齒的集中力,結合噪聲傳遞函數與集中力基于線性疊加法得到測點處噪聲預測模型。考慮諧波電流對轉矩脈動的影響,將噪聲預測模型代入遺傳算法對擬注入諧波電流的幅值與相位進行尋優。仿真結果表明:優化后的諧波電流能夠在不加劇轉矩脈動的前提下有效降低電機的振動噪聲。
1 驅動電機振動噪聲信號采集及分析
1.1 實驗設計與實施
本文研究對象為某永磁同步驅動電機,其主要性能參數如表1所示。在半消聲室中將被測電機聯接至測功機,并如圖1所示在距離電機外包絡面0.5 m測量面上布置傳聲器。采集電機在50%負載下從100 r/min勻加速至6 000 r/min時的瞬態振動噪聲信號,以及電機在各穩態轉速工況下的振動噪聲信號,穩態轉速以1 000 r/min為間隔選取1 000~6 000 r/min中的相應轉速。

表1 驅動電機主要性能參數

圖1 驅動電機噪聲信號采集測點布置
1.2 實驗數據處理與分析
對勻加速工況下各振動噪聲信號進行處理,得到全轉速振動噪聲信號頻譜圖,各測點的振動噪聲信號在頻譜圖上表現出相似的特征,圖2所示為Front測點全轉速噪聲信號頻譜圖。
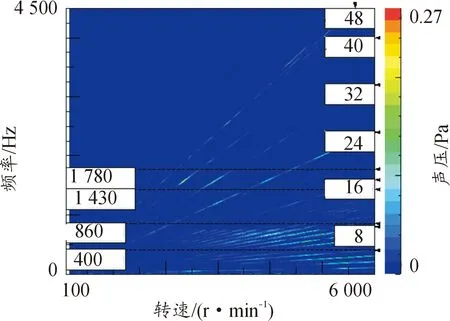
圖2 Front采集點噪聲信號頻譜圖
電機噪聲存在明顯的階次特征,對于本文所研究的8極48槽驅動電機,徑向電磁力的主要階次等于極數的整數倍次,而8階次作為最低階次,主要由永磁體基波磁場作用產生[3],較難采用優化諧波電流的方式減小,所以這種情況不予考慮。由于電機本身的模態特性,在頻譜圖上可以看到存在400~860 Hz和1 430~1 780 Hz 2個明顯的共振帶,較低頻的共振帶處于機械噪聲與較低階次的徑向電磁力活躍的頻段內,而在較高頻率的共振帶區間內,24、32、40階次的徑向電磁力所引起的噪聲有明顯的加強。根據各階次徑向電磁力的影響嚴重程度,本文選擇比較具有代表性的3 000 r/min轉速作為優化研究工況。
1.3 磁固聲仿真平臺建立與驗證
測點處的電機噪聲需要經過磁固聲耦合仿真計算得到,本文的仿真流程如圖3所示。將 3 000 r/min轉速工況下采樣得到的電流輸入二維電機模型中計算得到徑向電磁力,施加由節點力法計算得到的集中力至電機定子齒,將得到的電機殼體響應代入聲腔邊界元模型中計算得到測點噪聲。
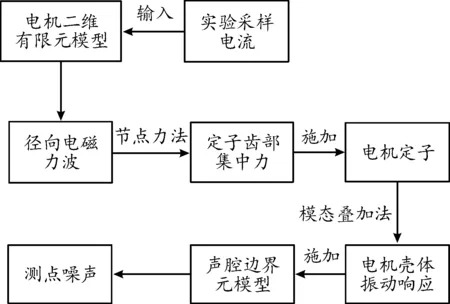
圖3 磁固聲仿真流程
其中,二維電機有限元模型根據表1參數建立,如圖4(a)所示,電機殼體聲腔模型如圖4(b)所示。
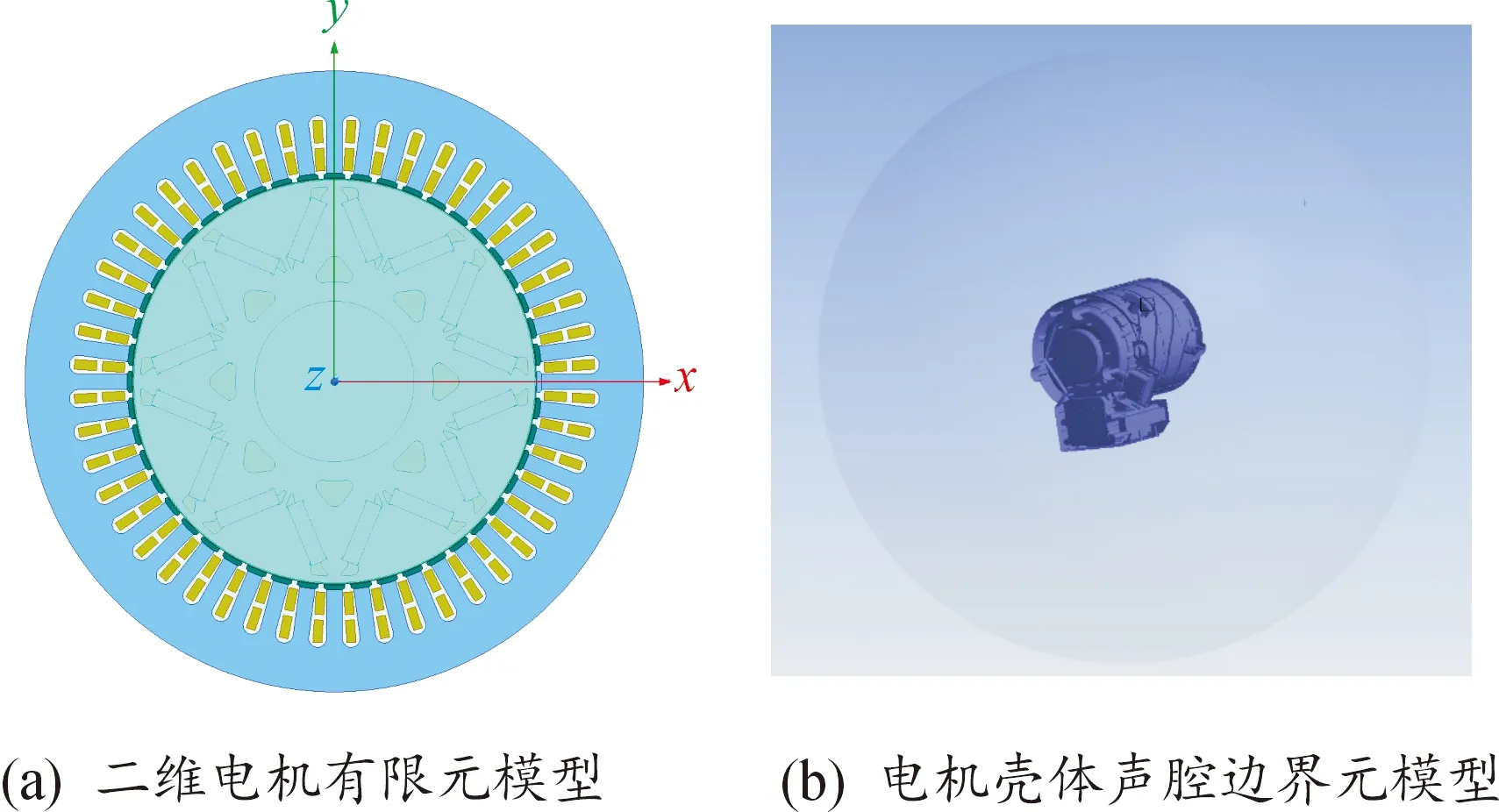
圖4 電機有限元及殼體聲腔邊界元模型示意圖
將仿真計算得到的噪聲信號與實驗采集得到的噪聲信號進行對比,如圖5所示。仿真信號在0~800 Hz之間的低頻段與實驗信號存在較大差異,因為該頻段的噪聲主要由軸承滾珠沖擊和電機轉子偏心等機械原因引起,對于研究所關注的低階次徑向電磁力所引起的噪聲,仿真信號與實驗信號保持了較高的一致性,說明該磁固聲仿真模型具有較高的準確性,可用于后續研究。
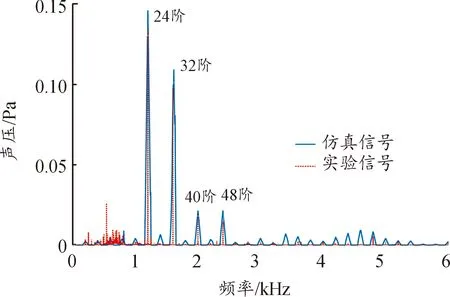
圖5 Front測點處噪聲仿真信號與實驗信號
2 徑向電磁力解析模型建立與階次分析
2.1 徑向電磁力解析模型
磁勢磁導法是電機主要的解析建模方法之一[11]。本文研究的驅動電機為永磁同步電機,其磁動勢由永磁體與繞組電流電樞反應兩部分疊加得來,永磁體與單相繞組電樞反應所引起磁動勢的解析式可以由式(1)、式(2)分別表示。永磁體與單相繞組電樞反應磁場產生的磁動勢均含有空間2k-1次諧波,并且永磁體所引起磁動勢的時間諧波來源于轉子運動時空間諧波的變化,而電樞反應引起磁動勢的時間諧波來源于繞組輸入諧波電流隨時間的變化,這使得電樞反應所引起磁動勢的時間屬性獨立于空間屬性。
(1)
(2)
u,v=2k-1,k=0,1,2,3,…
(3)
永磁體與電樞反應所引起磁動勢的各階次幅值可由式(4)與式(5)分別表示
(4)
(5)
式中:δ為氣隙長度;Br為永磁體剩磁;τm為極弧角;μ0為真空磁導率;kdv為繞組分布因數;kpv為節距因數;c為繞組層數;p為極對數;q為每極相槽數;N為線圈匝數;a為并聯支路數;m為電機相數。
為將電樞反應所引起磁勢的時間與空間屬性解耦,聯立式(2)(5)兩式并改寫如式(6)。式(6)將電樞反應所引起的磁動勢理解為繞組中通入的電流與單位電流下繞組產生的各空間階次磁動勢之積。
[Fhv_unitcos(vpα+φv)]
(6)
式中,Fhv_unit為單位電流作用下單相繞組產生的各空間階次磁動勢幅值。
氣隙磁密由磁動勢與氣隙磁導如式(7)所示相乘得到,而計算定子開槽后的氣隙磁動勢較為復雜[12],為獲得較為精確的考慮定子開槽的磁動勢幅值,本文施加單位電流至有限元模型中計算獲得單相繞組產生的各空間階次磁密。而三相繞組產生的磁密疊加后的表達式如式(8)所示。
(7)
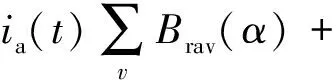
(8)
不同于繞組的靜態分布,永磁體磁動勢隨轉子轉動,所以需要計算氣隙比磁導以得到各轉動角度位置的永磁體磁密分布[13]。本文參考文獻[5]中提出的考慮徑向與切向磁密相互貢獻,通過有限元方法計算得到開槽前后的徑向與切向磁密空間分布,根據式(9)計算得到徑向比磁導。忽略切向磁密的貢獻,永磁體所引起的徑向磁密可由式(10)表示。
(9)
Brp(α,t)=Brps(α,t)λr(α)
(10)
式中:λr為徑向比磁導;Btp為開槽后切向磁密;Brps為未開槽時的徑向磁密;Btps為未開槽時的切向磁密。
根據麥克斯韋張量法,當不考慮幅值較小的氣隙磁密切向分量時,徑向電磁力波的表達式如式(11)所示。
(11)
將采樣電流分別輸入解析模型計算徑向電磁力,圖6為計算得到的氣隙徑向電磁力時空分布圖。將解析模型計算得到的結果與有限元模型進行時間與空間2個維度上的對比,如圖7所示。可以看到,解析模型計算結果與有限元模型相近,證明了解析模型的準確性。
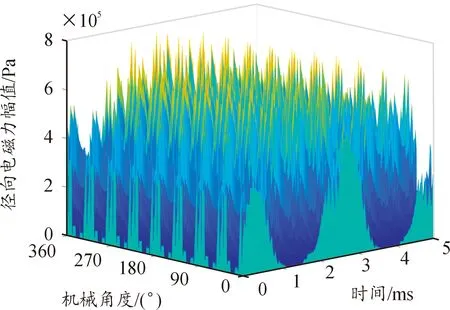
圖6 解析模型計算所得徑向電磁力時空分布圖

圖7 空間與時間維度下解析模型與 有限元模型徑向電磁力
2.2諧波電流對徑向電磁力貢獻分析
諧波電流通過影響電樞反應磁場影響電機徑向電磁力。為清楚地表示諧波電流引起的各時空階次磁場如何作用產生相應時空階次的徑向電磁力,將式(1)與式(2)代入式(11),并將諧波電流能夠影響的徑向電磁力來源列出得到式(12)所示的電樞反應磁場相互作用表達式,及式(13)所示電樞反應磁場與永磁體磁場相互作用表達式。
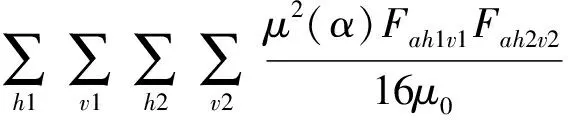
{cos((h1+h2)ω0t?(v1+v2)pα+
(φh1+φh2)?(φv1+φv2))+
cos((h1-h2)ω0t?(v1-v2)pθ+
(φh1-φh2)?(φv1-φv2))+
2cos((h1+h2)ω0t+(v1-v2)pθ+
φh1+φh2+φv1-φv2)+
2cos((h1-h2)ω0t+(v1+v2)pθ+
φh1-φh2+φv1+φv2)}
(12)

{cos((h+u)ω0t?(v+u)pθ+
(φh+φu)?(φv+φu))+
cos((h-u)ω0t?(v-u)pθ+
(φh-φu)?(φv-φu))+
cos((h+u)ω0t?(v-u)pθ+
(φh+φu)?(φv-φu))+
cos((h+u)ω0t+(u-v)pθ+
(φh+φu)+(φv-φu))+
cos((h-u)ω0t+(u-v)pθ+
(φh+φu)+(φv-φu))}
(13)
歸納得到如表2所示基波與諧波電流引起的磁動勢對各時間階次徑向電磁力的貢獻情況,需要注意的是,由于幅值較小,這里沒有考慮諧波電流引起的磁動勢之間相互作用的部分。在本文所研究的3 000 r/min轉速工況下,對測點噪聲影響最大的是8p及6p階次徑向電磁力,其主要由5次與7次諧波電流引起。

表2 各磁動勢分量對各階次徑向電磁力貢獻
圖8為3 000 r/min穩態轉速工況下電機采樣電流FFT分析頻譜圖,可以發現電機的主要諧波電流為5、7、11次,表3為三相電流中5、7次諧波的幅值與相位。
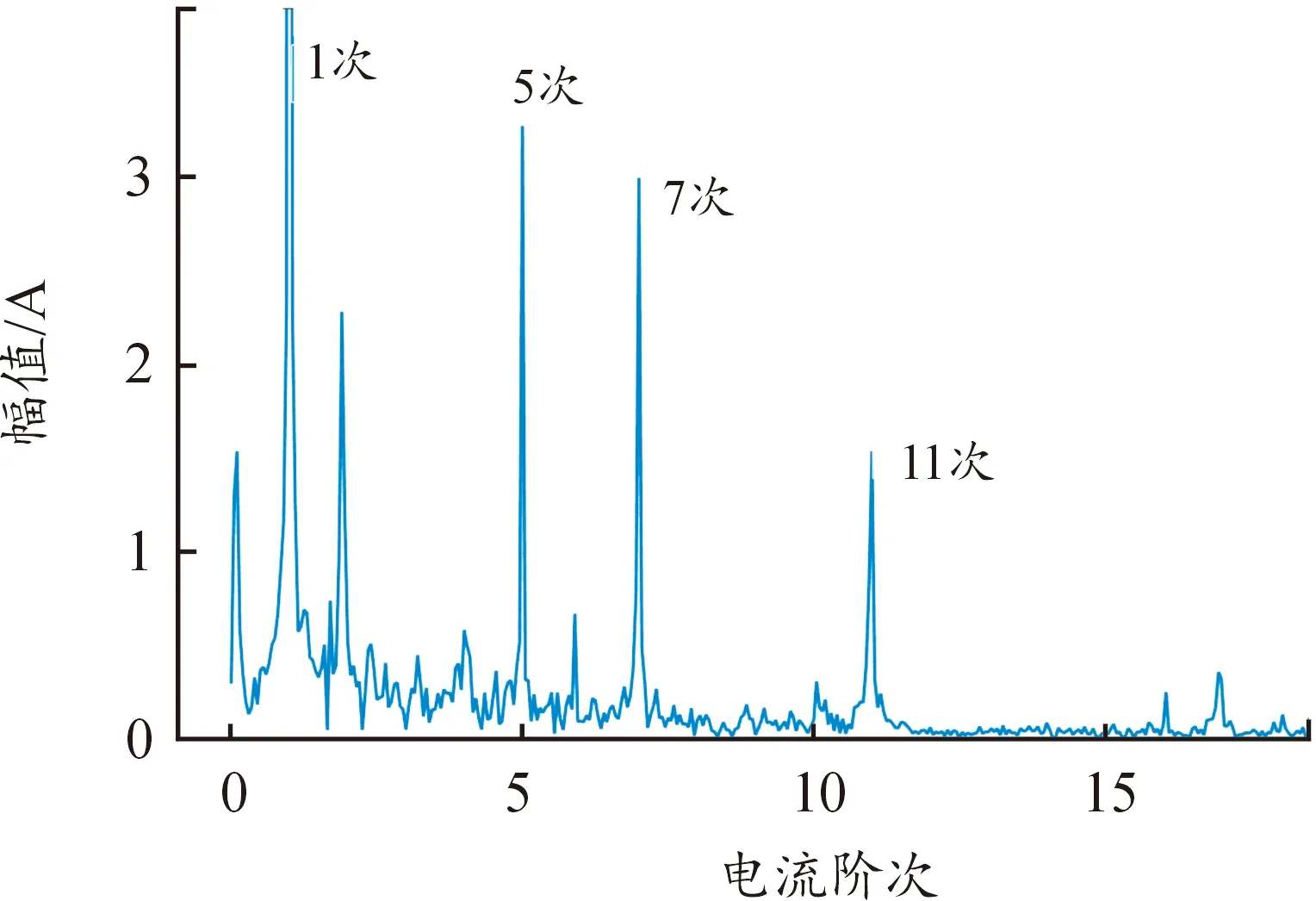
圖8 3 000 r/min下PMSM A相電流頻譜
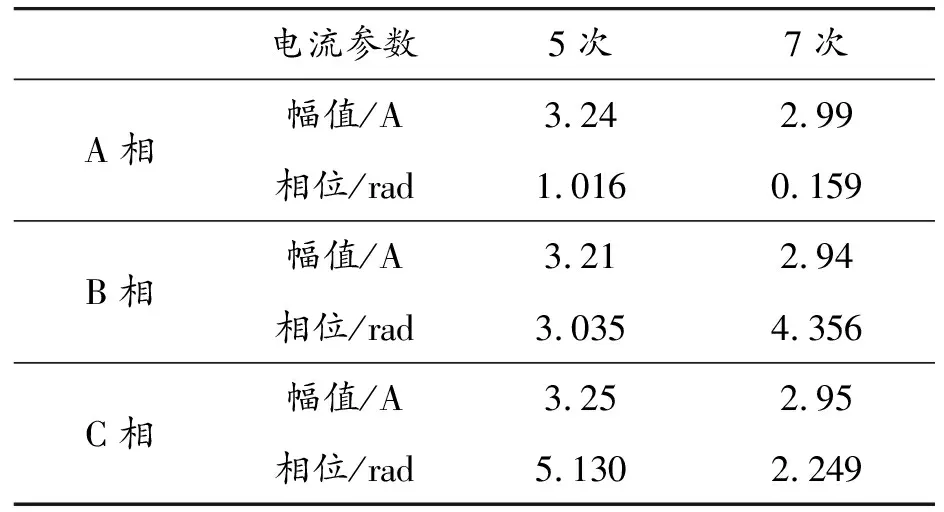
表3 三相電流各階次諧波參數
使用解析模型分別計算各磁動勢產生的8p與6p時間階次徑向電磁力,并表示在極坐標系上,如圖9所示。對于6p時間階次的徑向電磁力,其空間構成較為豐富,包括0、8與24空間階次,并且各階次均有相當的含量,其中由諧波電流引起的部分包括Fa1vFa5v、Fa5vFp1、Fa1vFa7v與Fa7vFp1。而對于8p時間階次的徑向電磁力,主要包含Fa1vFa7v與Fa7vFp1產生的8空間階次分量與Fp1Fp7、Fp1Fp9、Fa1vFp7、Fa1vFp9產生的32空間階次分量階次,并且由于是由永磁體磁勢或基波電流磁勢作用產生,這部分徑向電磁力無法通過調節諧波電流的方法進行改善。
結合徑向電磁力的極坐標分布,可以由2個角度對其優化,一是減小電流幅值以減小徑向電磁力幅值,二是調節諧波電流相位以優化各徑向電磁力之間的時間相位關系。
3 測點噪聲預測模型與貢獻量分析
3.1 定子齒部至噪聲測點傳遞函數分析
徑向電磁力波是作用在定轉子單位面積上的壓力,而作用于定子齒部的徑向電磁力對于電機的振動有決定性的影響[12],這部分徑向電磁力可以等效為作用在各齒冠面上的離散力,如圖10所示[14]。
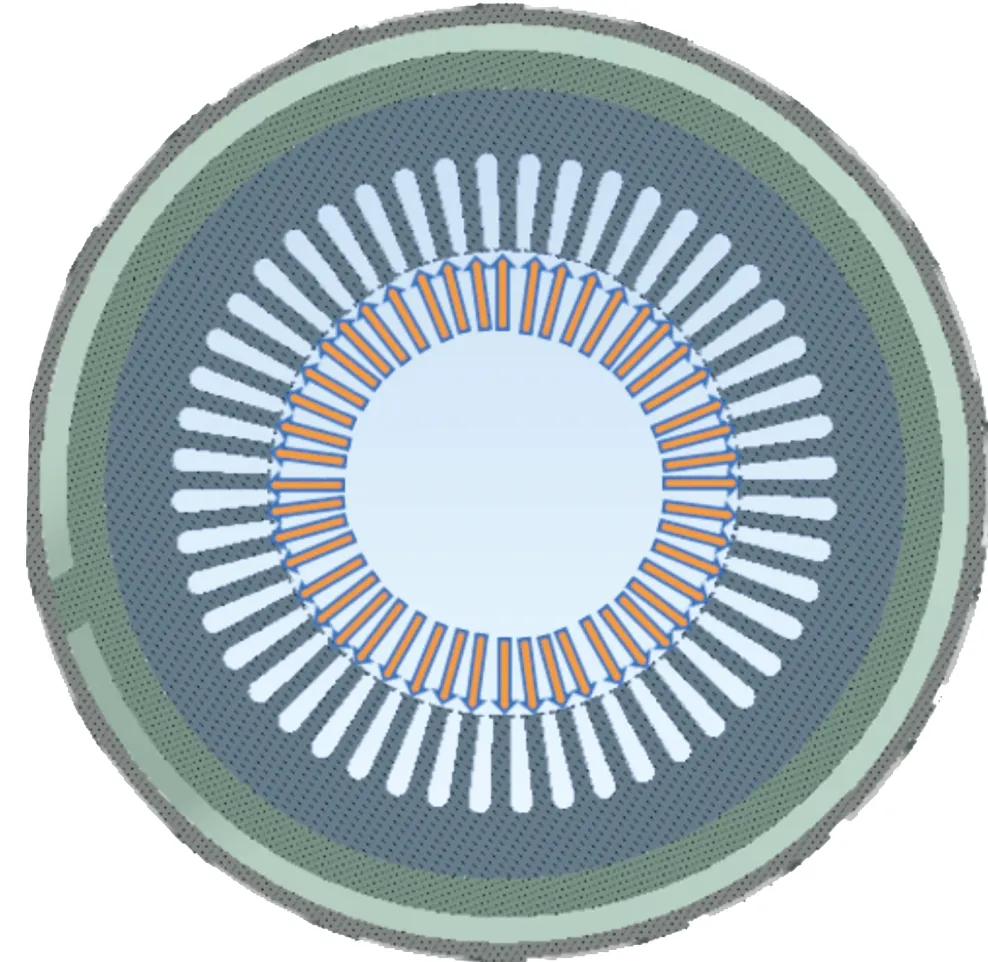
圖10 徑向電磁力作用于定子齒部示意圖
電機殼體的振動在一定振幅范圍內可以視作各定子齒上作用徑向電磁力所引起振動的線性疊加,如式(14)所示,而測點處的噪聲響應即疊加后所引起振動的輻射噪聲在測點處的響應,如式(15)所示。于是,各齒部激勵至測點處噪聲傳遞函數可以表示為式(16),為獲得測點處響應對于各定子齒處激勵的傳遞函數,分別將單位掃頻激勵作用于各定子齒,圖11為在某定子齒處施加單位掃頻激勵時測點噪聲傳遞函數曲線。
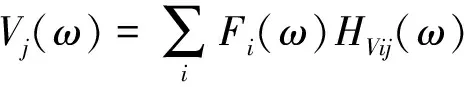
(14)
(15)
(16)
式中:Fi(ω)為各定子齒上的集中力,i=1,2,…,48;HVij(ω)為殼體某點處的振動響應對于定子齒處激勵的傳遞函數;HNj(ω)為噪聲測點處響應對于殼體各點處振動輻射的傳遞函數。
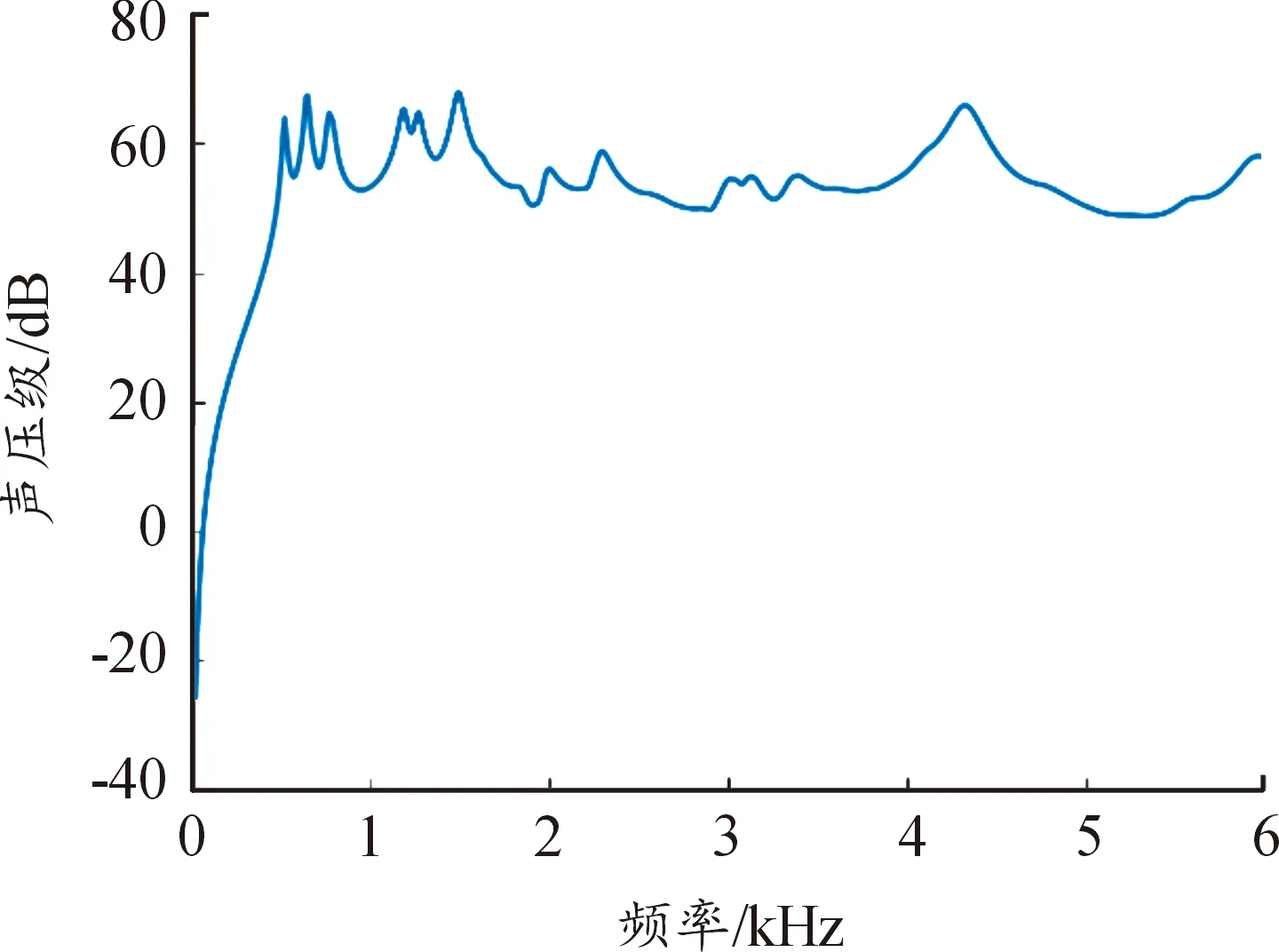
圖11 某一定子齒至測點處噪聲傳遞函數曲線
結合求得的48個齒部至噪聲測點傳遞函數,測點處噪聲預測模型由式(17)表示。
(17)
3.2 各時空階次徑向電磁力噪聲貢獻量分析
節點分布力法與面集中力加載法是計算徑向電磁力波對定子齒部作用力的2種方法,本文采用文獻[2]提及的面集中力加載法實現定子齒部集中力的計算。將每一個齒面的角度區間[α1,α2]四等分,并在每一個四分之一區間[βi,βi+1](i=0,1,2,3,4)應用柯特斯公式求解徑向電磁力波在齒面上的定積分,得到的復合柯特斯公式近似解如式(18)所示。
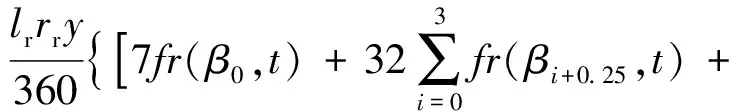
(18)
式中:lr為定子軸向長度;rr為定子中心至定子齒冠半徑;y為所求定子齒面在周向上的角度;βi+0.25=0.75βi+0.25βi+1;βi+0.5=0.5βi+0.5βi+1;βi+0.25=0.25βi+0.75βi+1。
將各磁動勢分量產生的6p與8p時間階次徑向電磁力波代入上式中進行計算,得到如圖12所示的各時空階次徑向電磁力在某一時刻作用于各齒部的集中力。根據奈奎斯特采樣定理,本文所研究的48槽定子對于24及以下的空間階次具有低通濾波效應[14],所以對于0、8、24空間階次的徑向電磁力波分量產生的作用于定子齒上的集中力能夠反映出空間階次特征,而對于32空間階次的徑向電磁力波,其產生的集中力的空間階次表現為16階次。

圖12 各磁動勢分量產生的集中力在各定子齒的分布
將各部分集中力代入噪聲預測模型中計算,得到表4所示各部分徑向電磁力對于測點聲壓對應頻率的貢獻量。由于測點聲壓是由各分量引起的噪聲疊加而成,所以表中部分分量引起的聲壓幅值大于總聲壓幅值。各階次噪聲的主要分量均由較低空間階次的分量引起,對于6p階次,0空間階次分量影響最大,而對于8p階次,并不存在0空間階次含量,但此頻率接近定子共振頻率,故8空間階次所引起的噪聲聲壓也較大。
4 基于遺傳算法的尋優與仿真驗證
諧波電流注入是一種抵消因逆變器非線性等原因而產生的固有諧波電流的重要方法,在抑制轉矩脈動等應用中具有廣泛的實踐經驗[15]。由于諧波電流對各時空階次徑向電磁力的影響較為復雜且相互之間存在耦合,采用遺傳算法對注入諧波電流的幅值與相位進行尋優。優化思路如圖13所示,將徑向電磁力解析模型與噪聲預測模型代入遺傳算法中參與尋優,同時考慮諧波電流對電機轉矩脈動的影響。
4.1 轉矩脈動的解析模型
電機的轉矩輸出可以視作齒槽轉矩tcog以及由電流與磁鏈相互作用產生的電磁轉矩te的線性疊加。齒槽轉矩不受諧波電流影響,且主要成分為電流頻率的12與24階次[16],可表示為式(19)所示的傅里葉級數。
t=te+tcog
(19)
tcog=Tcog12cos(12ω0t+φcog12)+
Tv24cos(24ω0t+φcog24)
(20)
式中:Tcog12、Tcog24分別是12階與24階齒槽轉矩的幅值;φcog12、φcog24分別是12階與24階齒槽轉矩的相位。
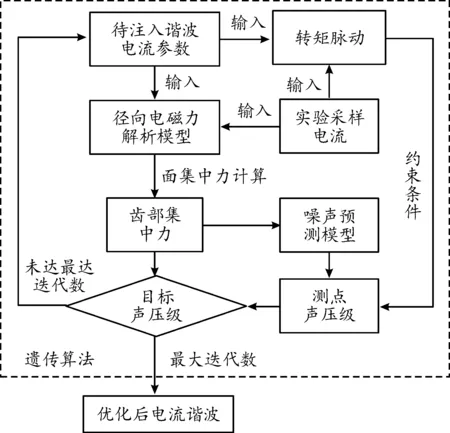
圖13 注入諧波電流參數優化思路
對于電磁轉矩,如式(21)所示,電流基波與磁鏈基波產生恒定轉矩,脈動轉矩部分主要由電流諧波與磁鏈基波,電流基波與磁鏈諧波以及電流諧波與磁鏈諧波3部分作用產生[17]。
te=1.5P(LdqIdq0+Λdq0)T×Idq0+
1.5P((LdqIdq0+Λdq0)T×idqh+
(21)
Λdq0= [Λ00]T
(22)
Idq0= [Id0Iq0]T
(23)
(24)
(25)
式中:Ldq為交直軸電感幅值;Λdq0為交直軸基波電流幅值;idqh為交直軸諧波電流;Λdq0為交直軸基波磁鏈幅值;λdqh為交直軸諧波磁鏈。
對比轉矩解析模型與有限元計算結果,如圖14所示,兩者在轉矩脈動特征上十分相似,最大脈動幅值均在21.1 N·m左右,精度足夠,可以代入尋優算法中進行計算。

圖14 轉矩輸出解析模型與有限元計算結果曲線
4.2 基于遺傳算法諧波電流參數尋優
由于3 000 r/min工況下對噪聲聲壓影響最大的是24階次與32階次所在頻率即1 200 Hz與1 600 Hz,于是,遺傳算法的適應度函數表示如下:
F=P(1 200)+P(1 600)
(26)
式中,P(f)表示某一頻率處的聲壓。
能夠對24階及32階噪聲產生影響的是5、7次諧波電流,所以優化參數為5、7次諧波電流的幅值與相位。
D=[Ia5,Ib5,Ic5,Ia7,Ib7,Ic7,
φa5,φb5,φc5,φa7,φb7,φc7]
(27)
參數之間滿足以下關系:
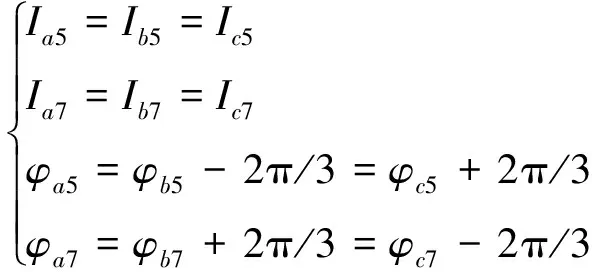
(28)
三相電流5、7次諧波可通過Park變換轉換至d-q軸坐標系上的6次諧波,注入的電流在d-q坐標系下可表示如下:
(29)
注入諧波電流與原有電流共同產生的轉矩輸出為:
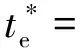
(30)
于是,為抑制轉矩脈動增大而設計的約束條件表示如下:
(31)
圖15所示為以測點聲壓為優化目標,基于遺傳算法對注入諧波電流幅值相位參數進行尋優得到的適應度函數。最終由遺傳算法計算得到的5、7次A相諧波電流的參數如表5所示,B、C相諧波電流可由式(28)計算得到。
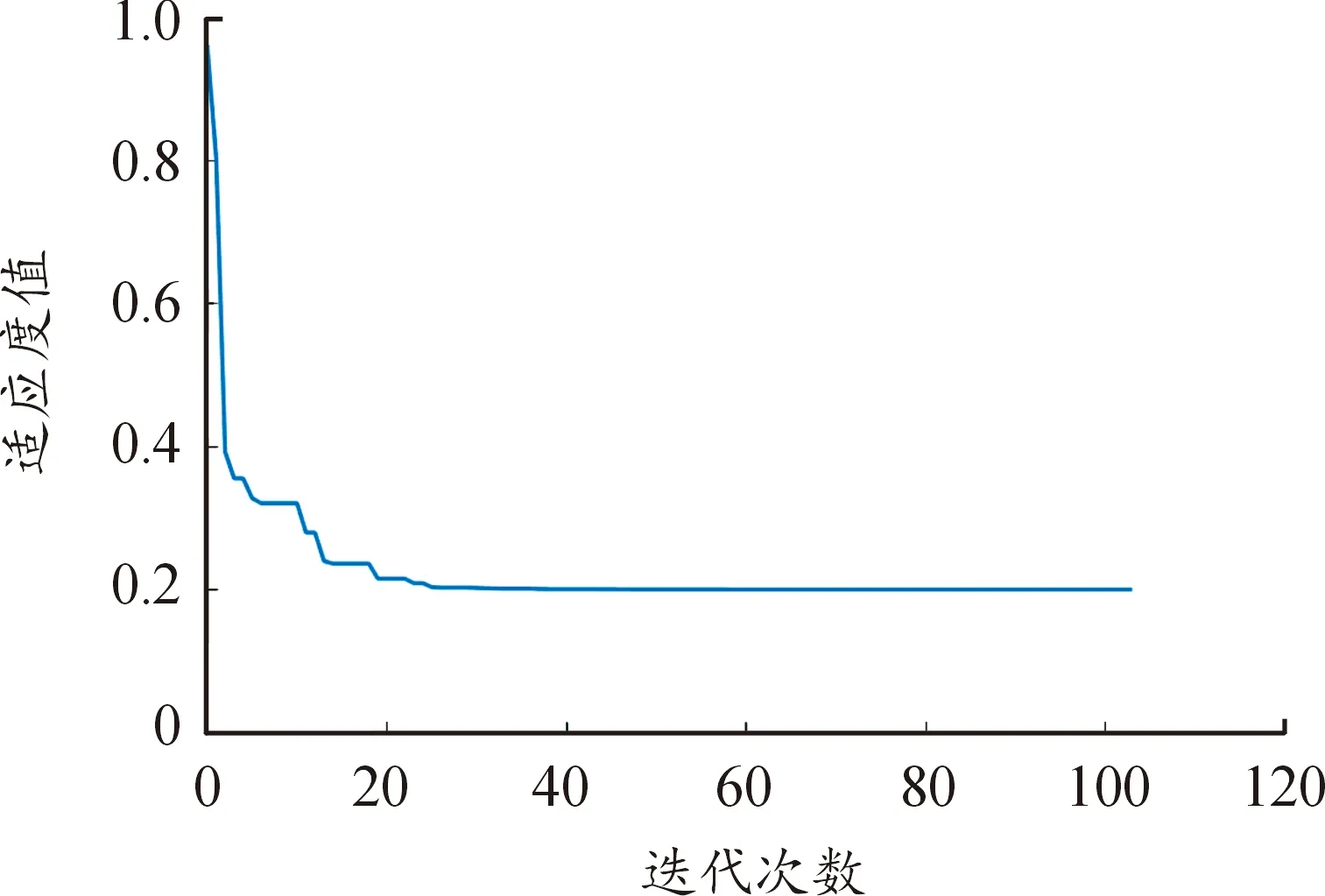
圖15 遺傳算法尋優諧波電流參數適應度變化曲線
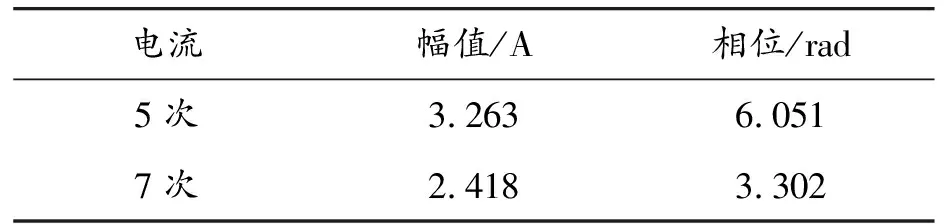
表5 注入A相諧波電流最優參數
4.3 基于磁固聲仿真平臺的驗證
為驗證注入優化后諧波電流對各階次噪聲及轉矩脈動的影響,將上述優化后的諧波電流與采樣電流疊加后代入已建立的磁固聲仿真平臺中,計算得到測點處聲壓與此時的轉矩輸出,分別如圖16—17所示。
表6歸納了各關注對象的優化效果,可以看到,本文重點關注的6p與8p階次噪聲在注入優化后的諧波電流后有明顯的降低,與此同時,電機的轉矩脈動也得到了有效的控制,沒有因為諧波電流的改變而惡化。
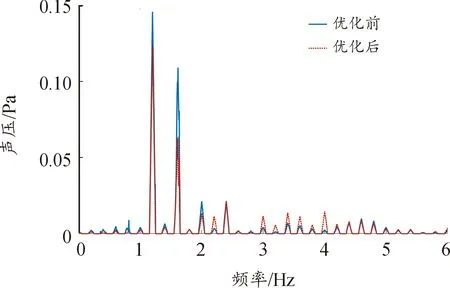
圖16 測點處響應曲線
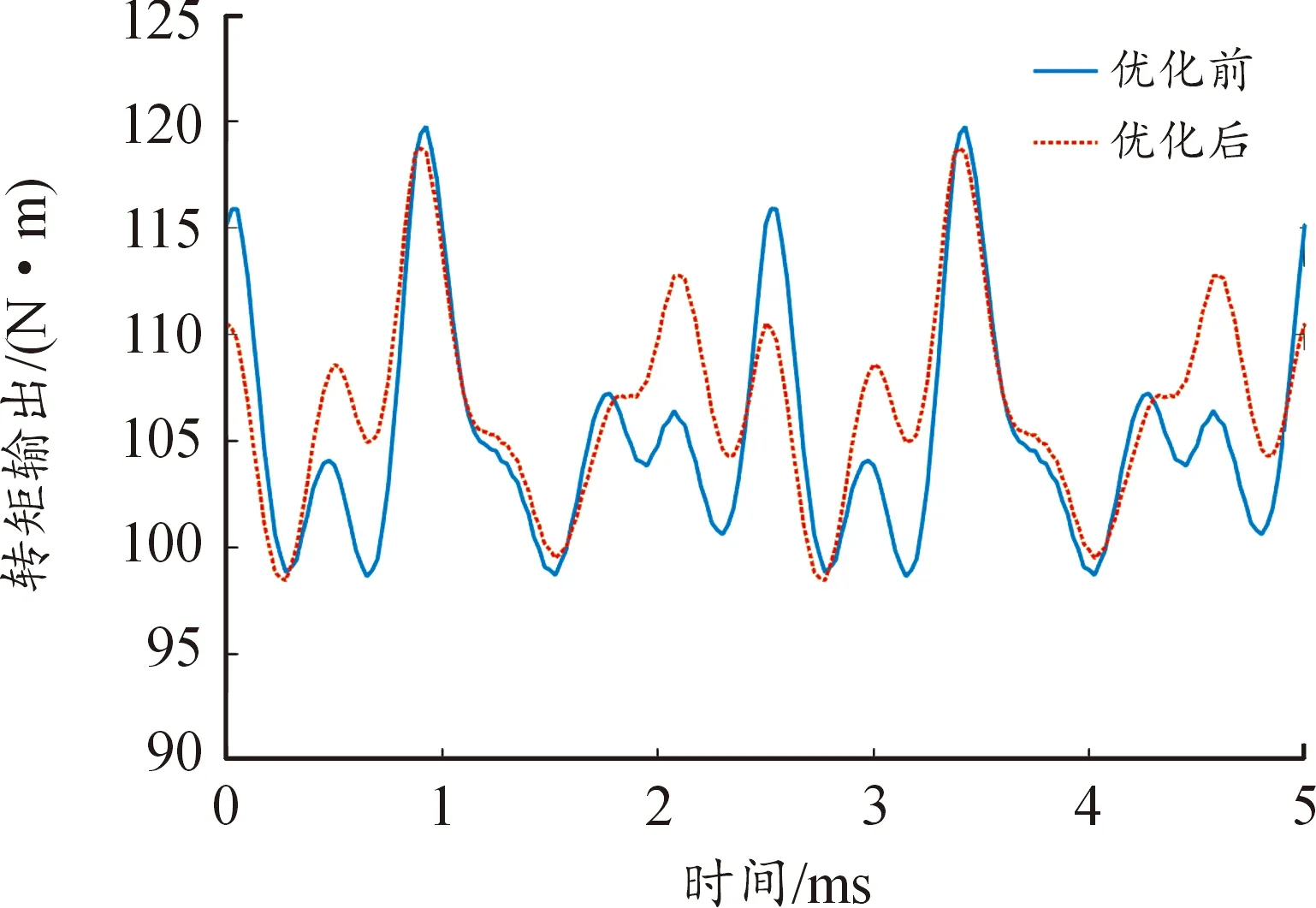
圖17 諧波電流優化前后轉矩輸出曲線
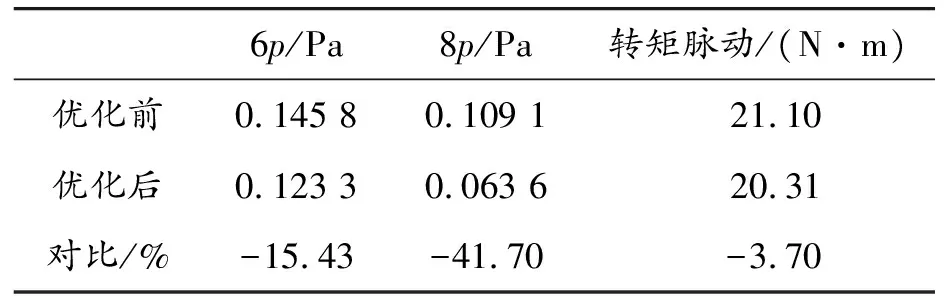
表6 諧波電流注入前后聲壓級與轉矩脈動
5 結論
1) 采集了某驅動電機的噪聲信號,分析噪聲信號的階次特征并認為6p與8p時間階次對噪聲聲壓影響最大。選擇3 000 r/min為研究工況,建立了磁固聲仿真模型并驗證了其在階次特征上與實驗信號一致。
2) 基于磁勢磁導法建立了徑向電磁力解析模型,通過與有限元模型計算結果的對比驗證了其準確性。根據諧波電流的階次特征分析各時空階次徑向電磁力的組成成分,并代入解析模型中計算得到各階次徑向電磁力分量的時空分布。
3) 基于線性疊加法通過有限元方法得到定子齒至噪聲測點傳遞函數,采用柯特斯公式計算各徑向電磁力分量作用于定子齒的集中力,實現各分量對噪聲測點聲壓的預測。基于預測模型,分析了各徑向電磁力分量對測點噪聲聲壓的貢獻量,確定了5、7次諧波電流對主要階次噪聲的影響最大。
4) 將徑向電磁力解析模型與噪聲預測模型代入遺傳算法中,在不增大電機轉矩脈動的前提下對擬注入的5、7次諧波電流參數進行尋優。仿真結果顯示,優化后的諧波電流能夠在避免惡化轉矩脈動的同時,有效減小主要階次噪聲。

