基于雙種群優化算法的艦載無人機任務規劃

樂健驛, 宋業新, 陳 洋

(海軍工程大學,湖北 武漢 430033)

0 引言

無人機(Unmanned Aerial Vehicle,UAV)自問世以來,在各個領域中都得到了廣泛的應用。在軍事應用方面,無人機以其具有的無生命危險性、大過載、高機動性和經濟可承受性等優點,使其備受青睞。軍用無人機也經歷了從任務簡單的靶機,到具備綜合偵察監控、空域巡邏、火力定位、實施精確打擊能力的察打一體無人機的發展。自上世紀九十年代以來,無人機在世界上各局部戰爭中使用的頻次逐步增多,尤其是近幾年爆發的敘利亞戰爭、納卡地區戰爭中,無人機群大量投入使用。因此,無人機協同任務規劃也成為各國學者研究的熱點問題之一[1～8]。在算法創新方面,文獻1針對多無人機協同搜索攻擊任務規劃問題,提出了智能自組織算法,將全局優化問題分解為多個局部優化問題,再通過無人機之間的信息交換,對整個系統做出最優決策。在應用背景與模型創新方面,文獻2根據多機場起降,多種偵查設備掛載的背景模型,利用改進的遺傳算法對最優偵查效率的問題進行了求解;文獻3,4考慮了各個任務的時間約束,分別采用了市場分布式拍賣算法與遺傳算法進行了求解。在任務規劃的魯棒性研究方面,文獻4～7分別以凸函數差分算法、魯棒過濾嵌入式任務分配算法、計算不確定多屬性決策問題的權值向量等方法,對不確定環境下多無人機協同任務規劃問題進行了求解。

從無人機任務規劃的應用背景來看,現有研究大多建立在陸基起降的無人機基礎之上,而艦載無人機的任務規劃有其自身特點。一方面,陸基起降的無人機,其放飛、著陸地點均為固定地點,而艦艇為移動平臺,其放飛點與著艦點均不固定,增加了問題求解的復雜度。另一方面,艦艇在海面航行過程中,不同海域的海洋環境不同,過大的海浪會導致艦體大幅度橫搖、縱搖、垂蕩,對無人機的離艦、著艦構成安全威脅,因此在任務區域內,只有部分海域適合無人機起降,而艦艇在適合無人機起降的海域內活動的時間有限,因此無人機起降存在時間約束。本文以艦載多無人機協同對海面目標攻擊的任務為背景,綜合考慮存在多個適合無人機起降海域的情況下,結合起降平臺的時間約束,對該任務規劃問題進行討論。

1 多艦載無人機協同海上目標攻擊問題的描述

1.1 問題的描述

設有一艘水面艦艇,艦艇上載有n架艦載無人機,對已知的海上m個固定目標進行協同攻擊。艦艇依次航行至適合無人機起降的海域,組織無人機放飛、著艦等活動。艦艇在組織無人機放飛、著艦的時候,會在該海域逗留一段時間,稱為窗口時間。無人機放飛以后,可以選擇不同路徑依次對目標進行攻擊,任務完成以后返回艦艇。為方便起見,將適合無人機起降的海域抽象為二維平面上的坐標點,稱為起降點。

無人機一共有兩個裝備外掛點,分別為武器外掛點以及電子干擾吊艙外掛點。武器外掛點可以選擇不同的裝備掛載,不同的武器對不同的目標能造成不同的損毀程度。而電子干擾吊艙外掛點只能選擇一種電子干擾吊艙掛載。電子干擾吊艙能有效對攻擊目標的反擊進行干擾,提高無人機的存活概率。而不同的裝備掛載選擇,使無人機產生的油耗不同,從而有不同的空中續航時間。因此要求無人機選擇合適的掛載裝備,起飛、著艦點,以及攻擊路徑,使得攻擊收益最高,而損毀概率最小。

1.2 基本假設與說明

1)無人機掛載武器攻擊距離有限,只有飛行至固定目標節點附近時,才能對該節點的目標進行攻擊,此時飛行距離近似為兩節點之間的距離。另外,無人機可以依次對不同目標進行攻擊,一架無人機對同一目標只攻擊一次。

2)無人機對目標的攻擊能瞬時完成,攻擊不額外耗費空中續航時間。

3)任務前需對任務海域內的海底暗礁、淺灘、水雷等威脅艦艇航行安全的因素進行綜合評估,艦艇航跡由任務前制定的航行計劃確定,每個起降點的時間窗口唯一。

4)無人機若不能在空中續航時間內順利返回艦艇,則因燃料耗盡而墜毀。

5)無人機返航后需要例行機械檢查,做日常保養維護,因此在任務期間,各無人機最多只能放飛一次。

2 無人機任務規劃模型的建立

2.1 符號描述

U={ui|1≤i≤n}為艦載無人機集合。

VS={vi|1≤i≤p}為起降點集合。

VT={vi|p+1≤i≤p+m}為攻擊的目標節點集合。

V=VS∪VT為所有節點集合。

T={tv|v∈VS}為艦艇在各個起降點對應的時間窗口集合。集合T中所有元素均為時間軸上的連續閉區間。

W={wi|1≤i≤l}為無人機所有可選擇掛載的武器集合。

cij,i,j∈V為無人機在該路徑上飛行所耗費的空中時間。無人機在該路徑上飛行所耗費空中時間與其飛行方向無關,即cij=cji。

ak表示第k個無人機在的總的造價成本,包括無人機自身造價成本與該無人機所有掛載裝備的造價成本。

Pk表示第k個無人機在任務路徑航行時被對方部署的防空武器造成毀傷概率的總和。

β∈(0,1)表示電子干擾吊艙的干擾效率。無人機未掛載電子干擾吊艙時,遭到反擊的毀傷概率為P,掛載以后的毀傷概率為P(1-β)。

τ(w,y),w∈W,y∈{0,1}表示無人機空中續航時間。該參數依賴于無人機掛載裝備的決策,其中w表示無人機掛載武器的選擇,y=0表示未掛載電子干擾吊艙,y=1表示掛載了電子干擾吊艙。

2.2 決策變量的描述

2.3 目標函數及約束條件

2.3.1 攻擊收益目標函數

無人機按照任務決策,依次對選定目標進行攻擊。因此該目標函數為全體無人機對所有目標的攻擊收益之和,要使其最大化。即:

(1)

(1)式中,目標節點j受到無人機攻擊造成毀傷概率總和為:

2.3.2 無人機損毀目標函數

無人機依照任務安排,在對目標進行依次攻擊時,在各路徑上將遇到對方防空火力的攻擊。該目標函數為全體無人機在路徑上損傷概率之和,要使其最小化,即:

(2)式中,單個無人機任務路徑航行時被對方部署的防空武器造成毀傷概率的總和為:

2.3.3 約束條件

約束條件(3)保證無人機在各路徑航行所耗費的空中續航時間要小于掛載裝備以后的最大續航時間,使其能在續航時間內完成預定的任務。

(4)

約束(4)表明無人機只能選擇一種武器掛載。

約束條件(5)表明無人機從任務起始節點出發,經歷任務所需時間以后,艦艇要處于其著艦點的窗口時間內,保證了無人機完成任務后能在預定時間內返回艦艇。

(6)

(7)

(8)

約束(6)、(7)、(8)保證無人機對每個任務目標只攻擊一次,且不會困在某一個任務節點中。

(9)

約束(9)保證無人機從艦艇出發,任務結束要回到艦艇。

3 利用雙種群優化算法求解

多無人機協同攻擊任務規劃問題是典型的NP-hard問題。和傳統的多無人機協同攻擊任務規劃相比,多艦載無人機協同海上目標攻擊任務規劃,存在無人機放飛點、返航著艦點的選擇不唯一,且放飛、返航著艦點都存在窗口時間,因此該問題的約束條件更強。以傳統的方法求解,算法很容易陷入收斂停滯,Pareto前沿的可行解更難以求得。本文采用雙種群算法[8](Double Population Optimization Algorithm,DPOA)對其進行求解。其步驟為:

第一步:初始化系統,設置可行解種群規模大小、不可行解種群規模大小、交叉概率、變異概率以及最大迭代次數。

第二步:隨機產生初始解,并按照約束條件,生成初代可行解種群,不可行解種群。

第三步:判斷迭代循環條件,若達到最大迭代次數則退出運算;若不滿足,進入第四步。

第四步:將可行解種群、不可行解種群分別依照預設概率進行交叉、變異,并對可行解種群、不可行解種群分別進行更新。

第五步:自增迭代次數,跳轉至第三步。

3.1 基因編碼及種群的更新

單無人機染色體編碼仍采用經典的編碼方式,以m+4維整數向量的編碼方式進行編碼,如式(10)所示:

(10)

其中,固定第一位染色體編碼為起降點VS中隨機一個元素,作為無人機放飛的起降點。第二位至第m+2位染色體,則為攻擊目標集VT與起降點集合VS中隨機的一個元素并集,并對其進行隨機排序,代表該無人機對各節點的依次訪問順序。當第i位編碼(1≤i≤m+2)為起降點集合VS中的元素時,表明該無人機已經規劃出從艦艇出發,返回艦艇著艦的簡單路徑,i+1～m+2位染色體標識的節點不再進行訪問。第m+3位染色體為0-1決策變量yk,標記該無人機是否掛載電子干擾吊艙,第m+4位染色體表示為掛載的武器編號。艦載無人機的全體染色體編碼,形成一個n×(m+4)的矩陣,便為一個完整的任務規劃方案。

由于染色體編碼為單個無人機的染色體向量組合而成的整數矩陣編碼,因此遺傳操作將矩陣編碼拆分為染色體向量,對應染色體向量進行交叉、變異再進行合并。染色體向量的遺傳操作與經典遺傳算法相同,本文的交叉算子采取部分映射交叉法,變異算子采取兩點互換變異[9]。

3.2 種群的更新

(11)

計算最劣Pareto等級個體的擁擠密度,刪除擁擠密度較小的個體,直到滿足種群規模要求。

不可行解種群的更新與可行解種群更新類似。若不可行解種群大小超過預設種群大小,則保留部分目標空間較優的個體,剔除目標空間劣勢個體。式(11)中dii為個體i與個體j在目標函數空間上的歐式距離,N為預設種群規模。

4 仿真實驗

4.1 參數的比較實驗

以3架艦載無人機協同對6個海上目標進行攻擊為例。仿真中主要參數設置如表1～表7所示。給定無人機造價成本為80。表1中,v0～v2為無人機起降點,v3～v8為攻擊目標節點。

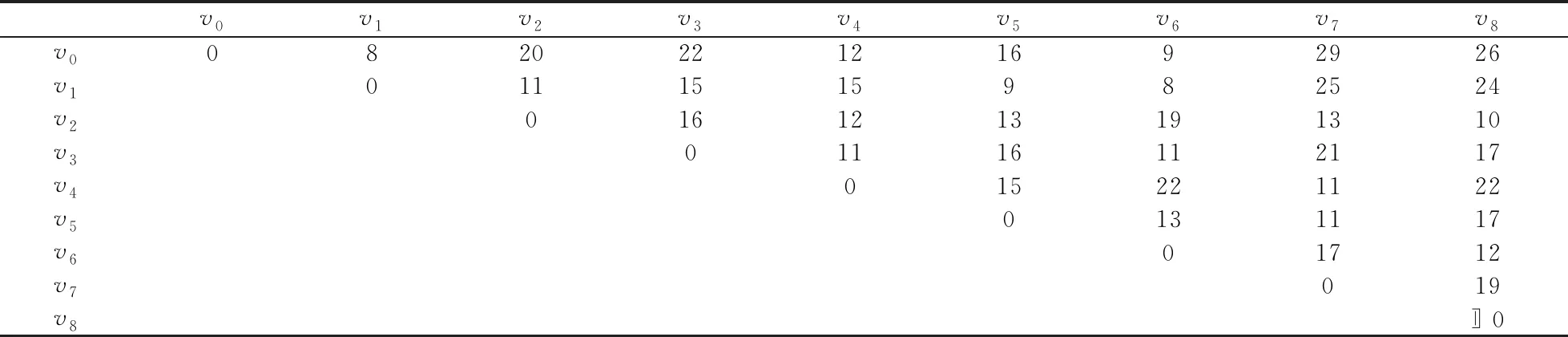
表1 無人機在各任務節點航行所耗費空中時間

表2 攻擊目標價值屬性

表3 各武器對目標的毀傷概率

表4 無人機空中續航時間

表5 無人機在各路徑航行被毀傷概率

表6 無人機掛載武器造價

表7 艦艇在各起降點的時間窗口

為驗證不同參數下算法的可行性與有效性,分別對部分參數進行調整進行縱向對比實驗。

算例1電子干擾吊艙造價成本為10,干擾吊艙的效率為0.8。

算例2電子干擾吊艙造價成本為80,干擾吊艙的效率為0.4。

算例3電子干擾吊艙造價成本為80,干擾吊艙的效率為0.8。

表8 算例1仿真結果

表9 算例2仿真結果

表10 算例3仿真結果

從仿真結果來看,各組解均為可行解。其中算例1、算例3中,電子干擾吊艙干擾效率較高,因此規劃結果中,各無人機均選擇掛載電子干擾吊艙。而算例2中,電子干擾吊艙干擾效率顯著下降,且造價提高,因此都沒選擇掛載電子干擾吊艙。在武器選擇方面,大多數都選擇對目標毀傷度較高的2號、3號攻擊武器,實驗結果符合客觀事實,任務規劃能達到預期效果。

4.2 算法性能的比較實驗

采取以經典的NSGA-2與SPEA2等多目標算法進行橫向對比實驗。為保證公平性,所有算法均采用相同的交叉、變異算子,交叉概率、變異概率和最大迭代次數均相同,分別為0.7、0.3、500。NSGA-2的最大種群規模為160;SPEA2初始種群規模為100,外部歸檔集種群規模為60,選擇策略為錦標賽選擇法。DPOA設置可行解種群為100,不可行解種群為60。

三種算法分別對4.1中的三個算例各進行80次實驗,并對實驗結果進行比較。實驗編程方法、運行環境與4.1相同。

為了定量評估算法的求解性能,采用文獻11中建議的反轉世代距離(Inverted Generational Distance,IGD)進行測試評估。其基本計算公式為:

(12)

式(12)中,P為給定算法在目標空間獲得的一個解集,P*為目標空間均勻分布的真實Pareto解集。d(z*,P*)為真實Pareto前沿上的點z*∈P*與P的最小歐氏距離,|P*|為P*的基數。由于本算例中真實Pareto解集為未知,因此P*取三種算法80次實驗結果并集的非支配解集進行近似替代。反轉世代距離越小,表示算法收斂性和解集的分布越好。

圖1～圖3分別為三個算例中各算法80次實驗全體解集的分布圖,表11為三個算例中各算法80次實驗的平均反轉世代距離以及平均計算耗時。

圖1 算例1中各算法解集的分布圖

圖2 算例2中各算法解集的分布圖

圖3 算例3中各算法解集的分布圖

表11 各算法的平均反轉世代距離與耗時

從圖1～圖3中可以看到,三種算法都收斂,但雙種群優化算法在本文算例中解集的分布與收斂情況更好。采用Wilcoxon秩和檢驗對各組反轉世代距離的實驗數據進行了顯著性比較,顯著性水平設置為0.05,雙種群優化算法顯著優于其他兩種算法。本文算例中,因存在時間窗口、以及空中續航時間的約束,可行解基因經過遺傳變異操作以后,可能變成不可行解,而不可行解基因經過遺傳變異操作以后,可能成為可行解。雙種群進化算法避免將可行解與不可行解進行直接比較,將可行解、不可行解同時迭代進化,從而能保留不可行解中的優秀基因片段,使算法有效避免陷入局部最優。

5 小結

本文研究了一種復雜海洋環境下移動起降平臺的艦載多無人機任務規劃問題,在這一問題的背景下,建立了多目標任務規劃模型。針對該模型約束條件強,傳統進化算法難以求解的特點,采用了雙種群進化算法,仿真結果驗證了該算法的可行性。但在算法方面,Harmonic距離要計算個體到種群中其他所有個體的目標空間歐式距離,計算量大,與其他經典優化算法相比,耗時更多。如何減少計算量,提高算法穩定性,還需要進一步深入探討。