考慮地震沖擊的自動化立體倉庫貨位分配方法

張水旺, 付林萍, 王 銳, 邵靈芝

(安徽工業大學 管理科學與工程學院,安徽 馬鞍山 243032)

0 引言

據中國地震臺網統計,自2019年1月1日至2021年5月1日,累計發生2524起地震事件,其中,震級5級以上1016起、6級以上259起、7級以上26起。地震發生會帶來許多損害,如,2018年初,沙二社區工業園的萬福隆購物商場,正常營業商場的倉庫夾層某貨架發生坍塌,引發“多米諾骨牌效應”,相鄰數排貨架相繼坍塌,導致員工、顧客被砸。同年,吉林松原市寧江區突發地震,某倉庫貨架受到地震影響全面坍塌,貨架發生連續倒塌。在地震沖擊下,倉儲中心是否能經得起地震考驗正常運營、能否避免巨大財產損失、為工作人員降低生命安全隱患,成為有現實意義的問題。因此,在貨位分配時有必要考慮貨架的抗震性,提高貨架的穩定性。

貨位分配[1]根據一些特定因素和原則,如貨架受力情況、周轉速度、響應效率、存儲空間、能耗節約等,對貨物的擺放位置進行指派的過程,科學的貨位分配方法可以縮短揀貨距離、降低搜尋時間、提高倉庫揀貨效率[2]。HAUSMAN[3]最早提出定位存儲、隨機存儲和分類存儲三種基本的貨位分配策略,之后的文獻分別根據不同的優化目標(如出入庫頻率[4]、貨架穩定性[5]、商品相關性[6]、空間利用率[7]等)對不同布局(如魚骨型[8]、Flying-V型[9]、多巷道式[10]等)的自動化倉庫貨位分配問題進行了廣泛深入的研究。

傳統研究貨位穩定性僅僅以三維空間中垂直方向的整體重心最低為優化目標,很少考慮由于突發自然災害等外力造成貨架坍塌的情況。在日常生產過程中,貨架并非一直處于滿載狀態,此時,貨物的分布方式也直接影響貨架結構的受力與安全[11]。因此,本文參考震區倉庫貨位分配策略[12]、自動化立體倉庫貨位分配[13]的研究成果,以地震力作用在整個貨架上的特性為基礎,研究貨物重力產生的力矩與地震水平方向的分力產生的力矩之間的關系以及它們對貨架穩定性的影響,同時綜合貨物出入庫能耗、關聯性等因素,構建多目標優化模型,采用FP-Tree和人工魚群算法(AFSA)[14,15]進行求解,并分析算法的優化性能。

1 問題描述及參數設置

1.1 問題描述

立體貨架,如圖1所示,由背靠背貨架和通道構成。目前大多企業采用隨機存儲策略,在訂單揀選過程中,經常發生錯揀、漏揀、延遲等情況,導致不能及時和準確發貨。貨位分配時若考慮貨物關聯規則,能有效降低貨物出入庫能耗,但堆放的位置不合理,極有可能造成貨架受力不均,地震發生時,地震產生的力矩對貨架產生作用,從而發生傾覆事故。因此,為了降低貨架坍塌的風險,本文在常用優化目標的基礎上,考慮地震沖擊,對立體貨架貨位分配問題進行研究。

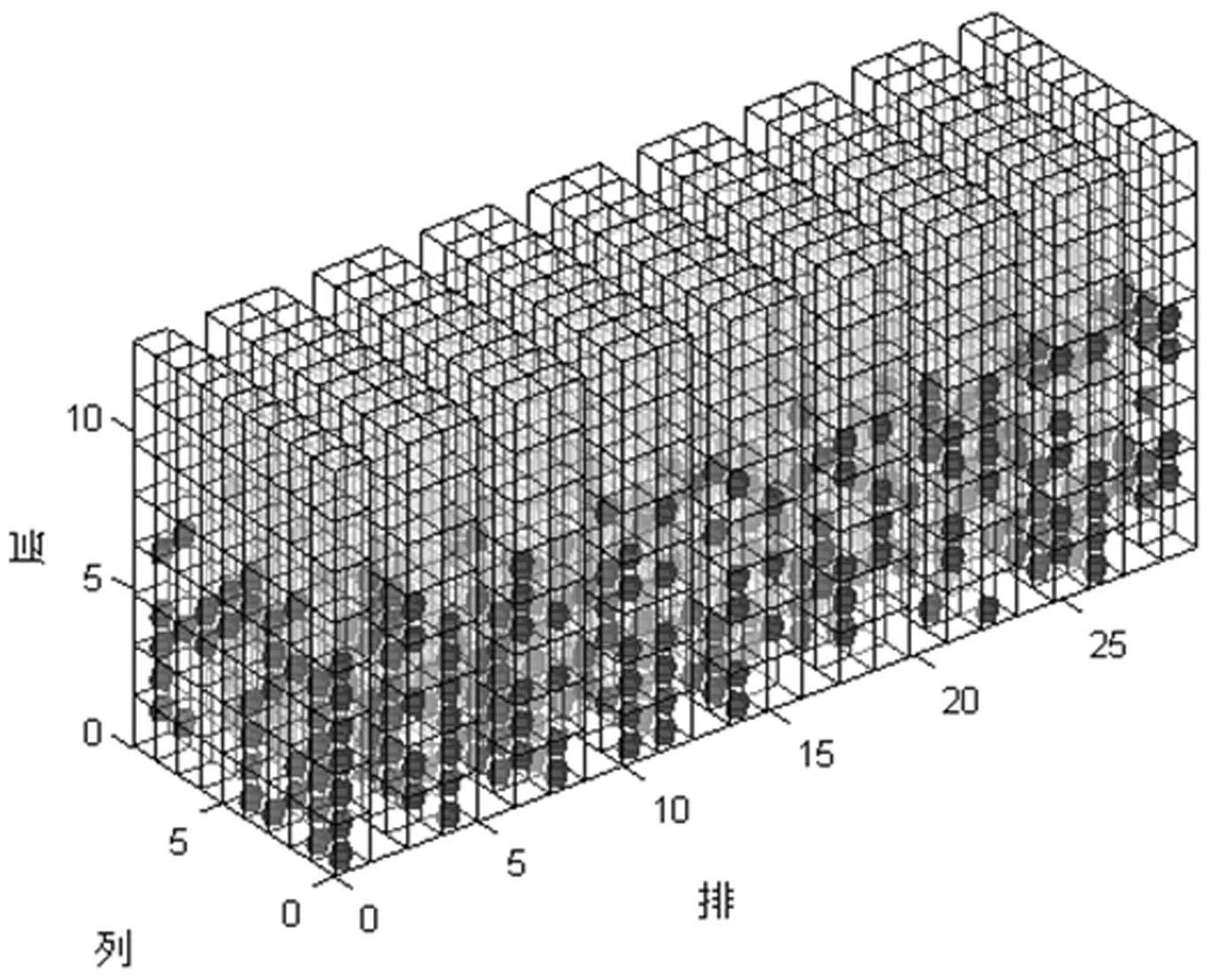
圖1 立體貨架示意圖

1.2 參數設置

φ:水平地震影響系數;

λ:結構等效總重力荷載系數;

μ:摩擦系數;

g:重力加速度;

r:表示第r排貨架,且r∈{1,2,…,R},R為貨架總排數;

s:表示第s列貨架,且s∈{1,2,…,S},S為貨架總列數;

l:表示第l層貨架,且l∈{1,2,…,L},L為貨架總層數;

m:質量,mrsl表示r排s列l層貨位上貨物的質量;

h,d,w:貨位的高度、深度和寬度;

T:背靠背相鄰貨架縫隙的連接長度;

ersl:從原點到貨位(r,s,l)的單位能耗;

D:相鄰兩通道之間的距離;

Dr:貨位原點至指定貨位r方向的距離;

J:獲取頻繁項集的數量;

pj:頻繁集對應的支持度,作為貨物的出入庫頻率;

I:每頻繁項集包含的商品品類數。

Mg:表示重力作用產生的力矩;

Msx:表示地震沖擊力作用產生的力矩。

2 模型構建

2.1 基本假設

假設1商品與貨位的尺寸相適應,一個貨位只能存放一品貨物,貨物以整箱為單位存儲在貨位上;

假設2貨位規格相同,且在模型中將貨位處理成三維坐標的點;

假設3貨物出入庫距離參考貨位與貨架原點的直線距離。定義原點坐標為(0,0,0)。

2.2 多目標模型

2.2.1 貨物出入庫能耗

為減少貨物出入庫能耗,常用的方法是在靠近倉庫出入口的位置儲存那些出入庫頻率高的貨物。基于此,用出入庫頻率和耗能作為衡量標準,建立貨物出入庫能耗的數學模型:

ersl=μ×g×Dr×D+μ×g×w×(s-1/2)+

g×(l-1/2)×h

(1)

(2)

其中,i=1,2,…,I,j=1,2,…,j。當r為奇數時,Dr=r·D/2;當r為偶數時,Dr=(r-1)·D/2。

2.2.2 貨架穩定性

由于大多數倉儲中心貨架都是固定的,不會發生貨架整體滑動的情況,在此僅考慮貨架發生靜摩擦的情況。根據對貨架存儲的貨物進行受力分析,可知Msx≤Mg才能保證貨架穩定性。為方便對多目標函數進行歸一化處理,在構造貨架穩定性目標函數時求其最小值,即Msx-Mg的值越小最好,由此構建貨架穩定性數學模型:

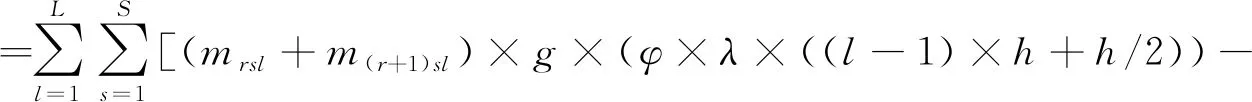
(mrsl×d/2+m(r+1)sl×(T+3d/2)×g)]

(3)

其中,r為偶數。

2.2.3 頻繁項就近存儲

依據貨物之間的關聯規則,對頻繁項集中的頻繁項就近存儲。參考文獻14,建立數學模型:

(4)

其中,|mi-m(i+1)|≤min{mi,m(i+1)}。

2.3 目標函數變形

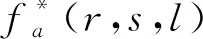
3 算法設計

3.1 人工魚群算法(AFSA)步驟

(1)參數設置;

(2)對問題進行編碼。在本問題中,每條染色體代表一品貨位分配方式;

(3)初始化。利用zeros函數隨機產生初始種群;

(4)計算適應度函數值。在適應度函數中代入每個解,求得染色體的適應度函數值,選擇最優的人工魚狀態,賦予公告牌;

(5)個體選擇。每條人工魚在評價后,自行選擇聚群、覓食或追尾行為;

(6)更新個體及適應度;

(7)算法終止。若滿足終止條件,算法終止,否則,返回第三步。

3.2 編碼及編號設計

依據評價目標函數將貨物重新分配到貨位,貨物是以整箱為單位存儲在貨架,貨位與貨物存在一一對應關系,因此,適合采用實數編碼,一條人工魚代表一種貨位分配方式,其中w為需要分配貨位的貨物數量。

(1)編號由一維轉化為三維。貨架里的貨位從左至右、自下而上順序編號,如圖2所示,用u(w)表示第w號貨物對應的一維編號。利用式(6)將u(w)轉化為三維向量(x,y,z)。

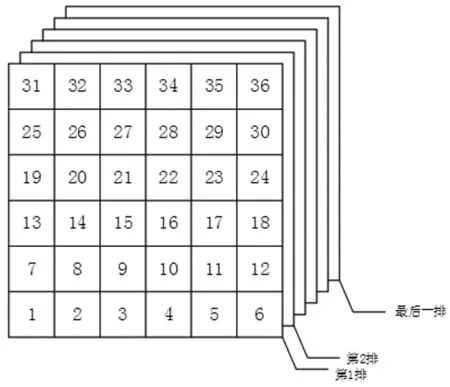
圖2 貨位編號順序

(2)編號由三維轉化為一維。導入初始信息,如出入庫頻率、重量、初始三維坐標等,將貨物的三維貨位編號(r,s,l)通過式(7)轉化為貨物的一維貨位編號u(w)。

u(w)=(r-1)×s×l+s+(l+1)×s

(7)

(3)同層背靠背貨位編號。三維倉庫模型中同層背靠背貨位編號之間的關系如圖3所示,例如,第2排第1層第1列的貨位編號為67,第3排第1層第1列的貨位編號為108,由此可知編號67貨位相鄰排同層貨位的編號為108,其他同層背靠背貨位之間的關系依此類推。

總結分析得出式(8),可求出對應的同層背靠背貨位編號。

u(w)=[(x-1)×s×l+y+(z-1)×s]+

[(s-1)×l+1]+2×(l-y)

(8)

4 仿真實驗

4.1 數據準備

通過對某電商倉進行數據調研,獲取了670品貨物的初始信息和1660條樣本訂單信息,包括編號、重量和原始坐標(貨位)等。同時獲得模型參數如下:h,d,w依次為1.2米、1米和1.6米;r,s,l分別為16、9、8;D為3.7米;μ和g分別為0.5和10;λ、φ、T分別為0.85、0.08、0.5米。運用FP-Tree算法對樣本訂單進行挖掘。

(1)導入初始信息;

(2)累加樣本訂單中貨物出現的次數,得到貨物的出入庫次數,作為出入庫頻率;

(3)將閾值設置為150,如果I1?I2的支持度大于150,那意味著I1?I2是頻繁項集;

(4)運行FP-Tree算法程序,獲得初始頻繁項集,從中篩選出二項頻繁項集。

(5)為保證貨架局部穩定性,設置頻繁項貨物重量差滿足式(9)約束:

|mi-m(i+1)|≤min{mi,m(i+1)}

(9)

(6)獲取頻繁項集。

4.2 適應度函數確定

4.3 算例求解

為驗證本文算法解決該問題及模型的有效性,將670品貨物分配至1152個貨位,求優化后的貨位分配方式,同時生成1660條客戶訂單,計算訂單揀選總距離。

參照文獻14、15對AFSA參數與優化結果關系的研究,設置人工魚數量為60、視野為100、擁擠度因子為0.8、最大試探次數為200、最大迭代次數為3500。通過仿真模擬,得到優化后的貨位分配結果,如圖4所示。此時,總目標值為0.5375,相比優化前的4.5821降低了88.2696%;優化后方案對應訂單的揀選距離為12474米,相比初始揀選距離16140米降低了22.7138%。

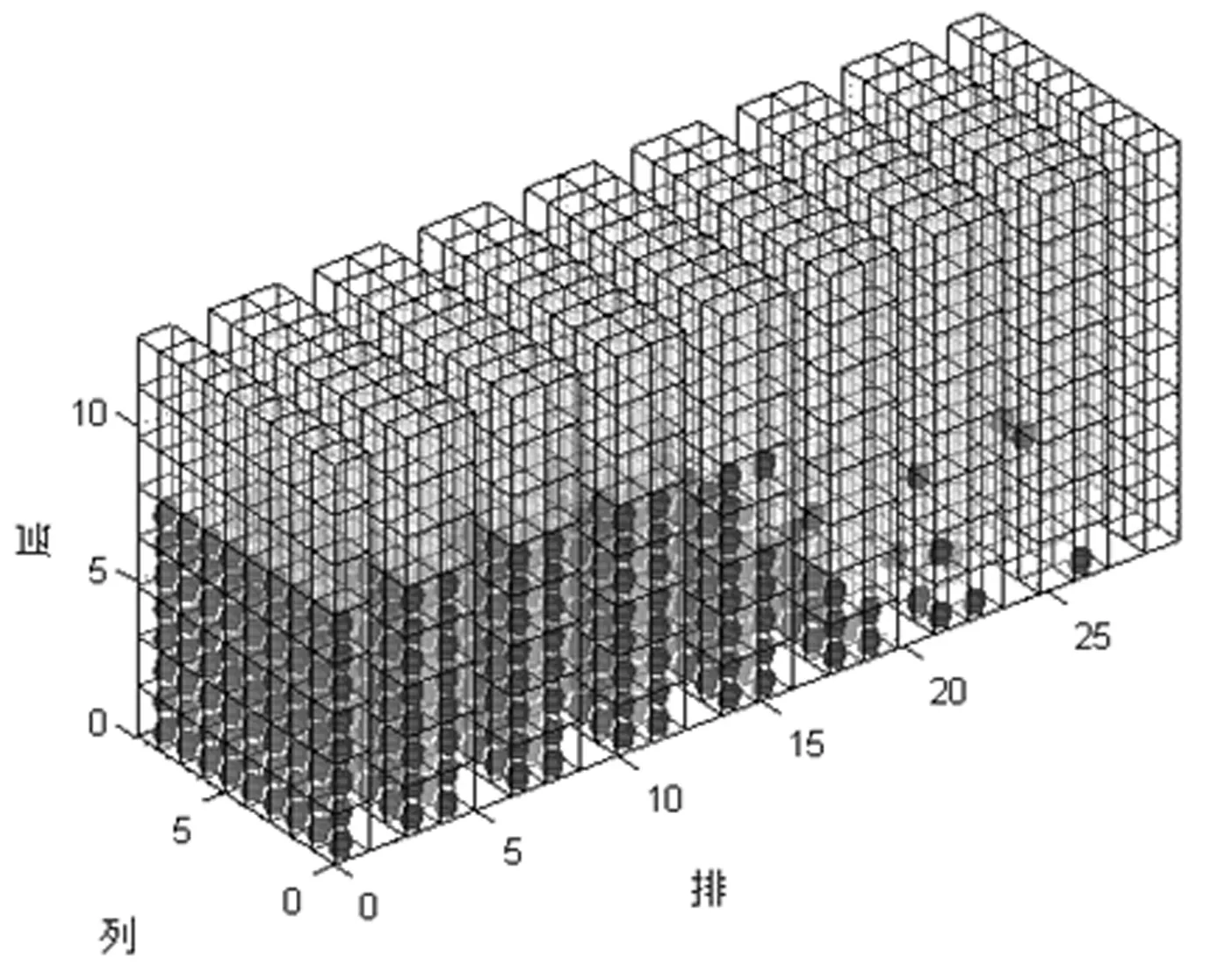
圖4 優化后貨物存儲圖

4.4 結果分析

4.4.1 考慮地震沖擊對求解結果的影響

結合前述的貨架穩定性原理,當目標函數二的求解結果小于零時,其結果取絕對值后越大,則說明該貨位分配方案的貨架穩定性更高,因此,為了更加清晰地比較貨架穩定性高低,當求解結果小于零時,取優化后結果的絕對值作為評價貨架穩定性高低的依據。用情形1和情形2依次表示未考慮地震沖擊的貨位分配優化方法和考慮地震沖擊的貨位分配優化方法,結果如表1所示。

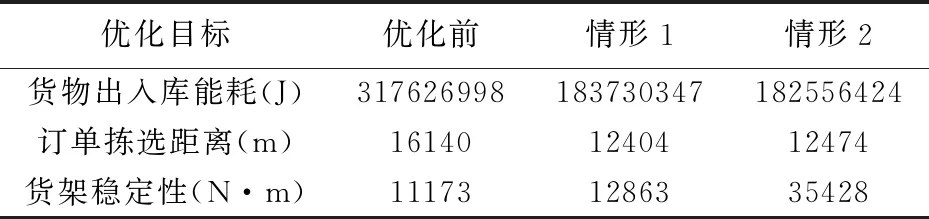
表1 不同情形下各目標優化結果

未考慮地震沖擊的貨位分配方案中貨物出入庫能耗較優化前降低了42.1553%,而考慮地震沖擊的貨位分配方案中貨物出入庫能耗較優化前降低了42.5249%;情形1優化后訂單的揀選距離比優化前揀選距離降低了23.1475%,而情形2優化后訂單的揀選距離降低了22.7138%;情形1優化后貨架穩定性比優化前的貨架整體穩定性提高了15.1257%,而情形2優化后貨架穩定性提高了217.0858%。

貨物出入庫能耗和訂單揀選距離在兩種情形下的優化效果基本相同,但情形2優化后貨架穩定性比情形1優化后貨架穩定性更強,因此考慮地震沖擊的貨位分配方案在未降低貨物出入庫能耗和訂單揀選效率優化效果的基礎上,提高了貨架的整體穩定性,增強了貨架抵御地震沖擊的能力。

4.4.2φ對求解結果的影響

根據《抗震規范》(GB50011-2010)可得不同地震烈度對應的水平地震影響系數,如表2所示。改變φ,其他變量均保持不變,分析φ對求解結果的影響。

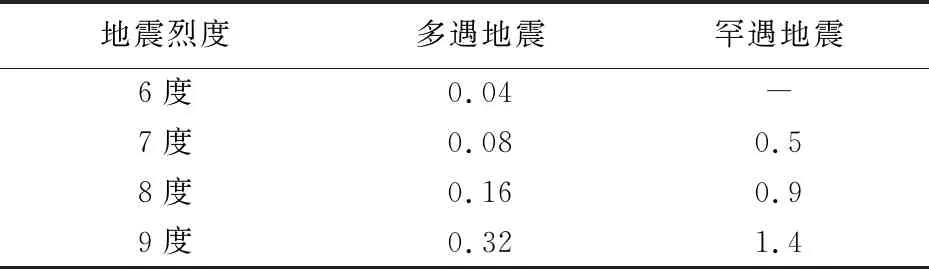
表2 水平地震影響系數

在多遇地震地區的不同地震烈度情況下,本文方法都能使總目標值優化效果達到87%以上,說明該算法對于不同烈度地區的倉庫貨位優化問題都具有適用性,能降低倉庫貨物出入庫能耗、提高貨架穩定性。需要說明的是,在多遇地震地區,水平地震影響系數小于0.24,即地震烈度低于8度時,隨著水平地震系數的擴大,總目標的優化效果越明顯,當水平地震影響系數到達0.32,即地震烈度為9度時,更多的不確定因素出現,優化效果有所下降,如圖5所示。

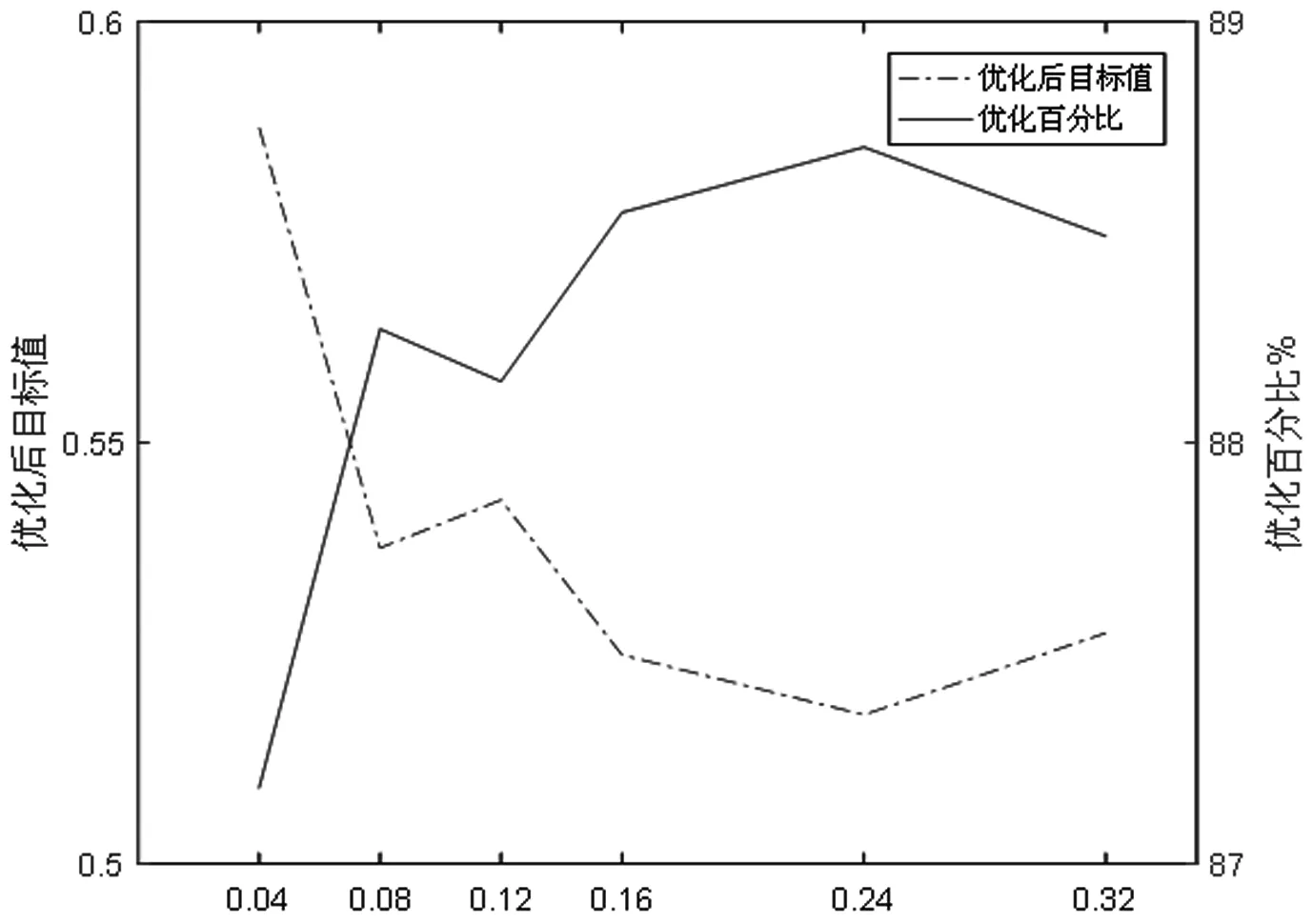
圖5 多遇地震地區φ求解結果的影響

在罕遇地震地區的不同地震烈度情況下,本文提出的模型和算法都能使總目標值優化效果達到88%以上,如圖6所示。說明該算法對于不同烈度地區的倉庫貨位優化問題都具有適用性,能降低倉庫貨物出入庫能耗、提高貨架穩定性。

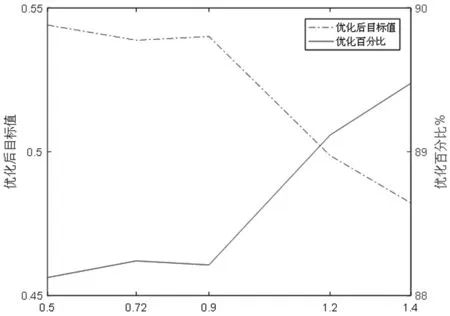
圖6 罕遇地震地區φ求解結果的影響

4.4.3 不同算法對求解結果的影響

本文算法選擇和遺傳算法(GA)、粒子群算法(PSO)進行對比,三種算法運行結果如圖7所示。

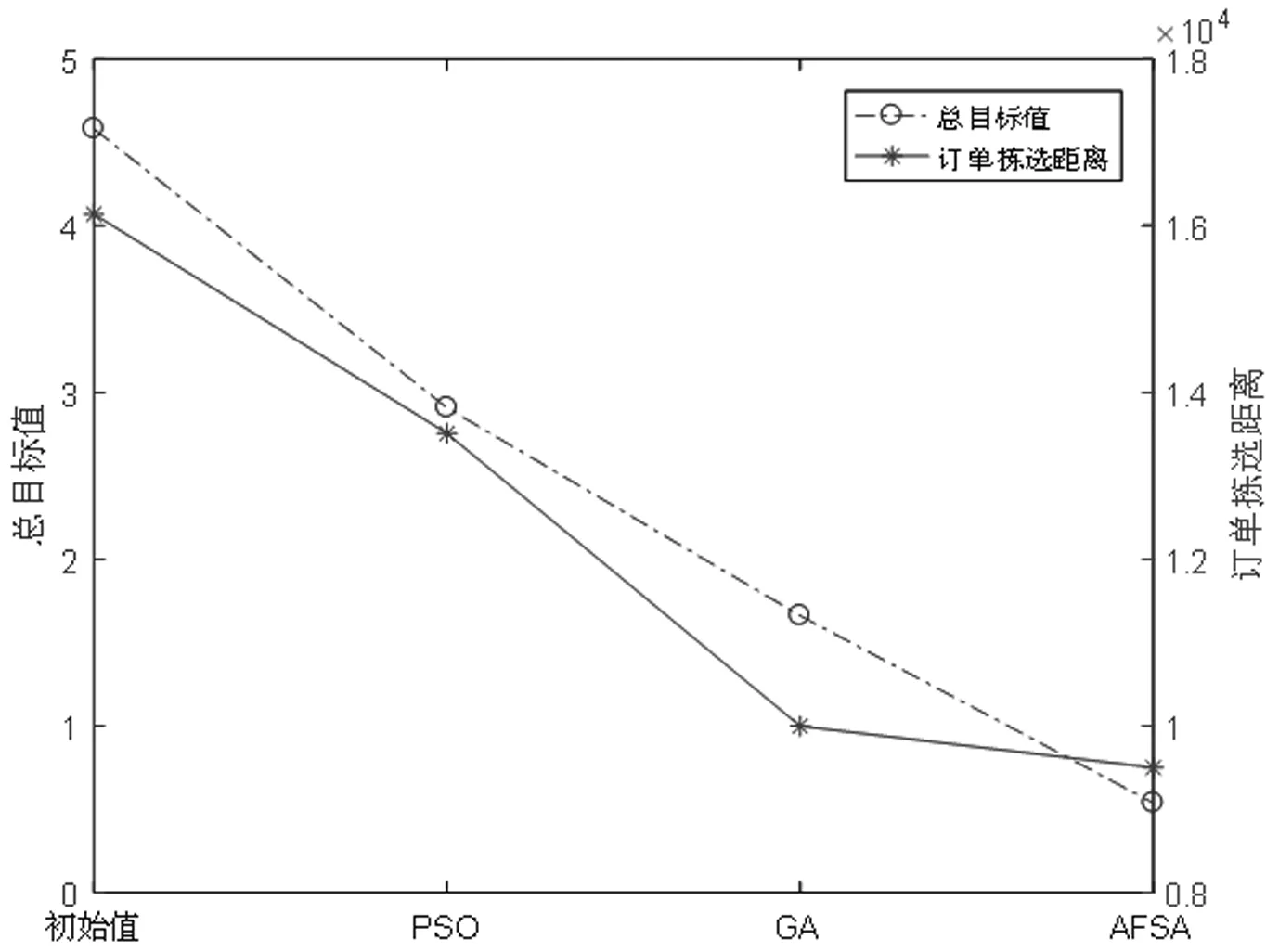
圖7 不同算法結果對比圖

PSO、GA對總目標的優化效果分別為36.5356%、63.7481%,訂單揀選距離依次為13510、9996,優化效果依次為16.2949%、38.0669%,而AFSA無論從總目標值,還是從訂單揀選距離來說,優化效果都要好。

PSO的優化速度在三個算法中優化速度最慢,且優化效果最差;GA在前100次迭代中,最優值的下降速度很快,但在迭代1000次后,問題的解并沒有進一步優化,該算法收斂速度較快,但容易陷入局部最優;AFSA的優化效果較前兩者的優化效果更為顯著,如圖8所示。

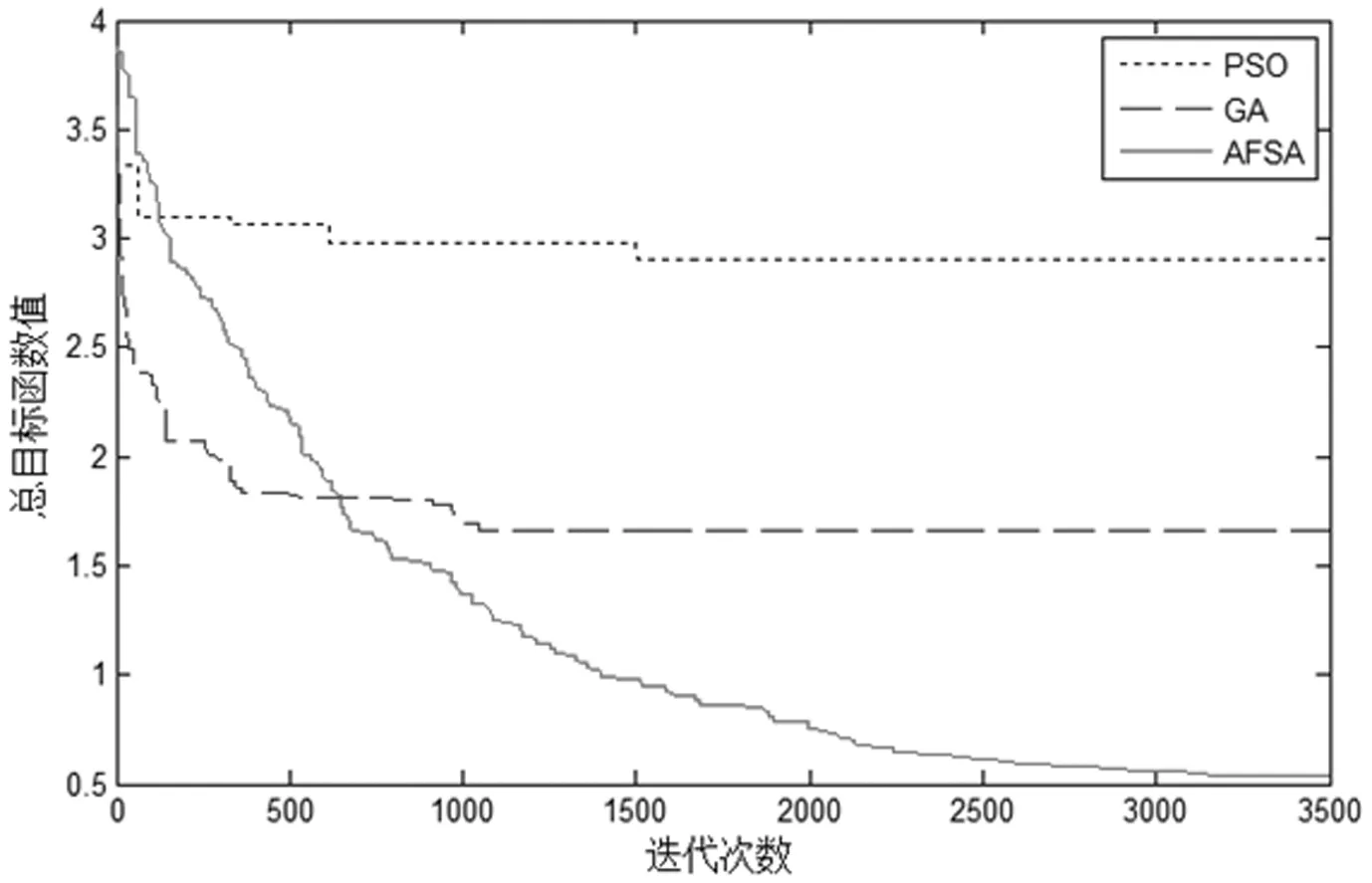
圖8 算法收斂曲線對比圖

5 結論

本文在考慮地震沖擊的情況下,建立了以貨物出入庫能耗、貨架穩定性及頻繁項距離最小化的多目標優化模型,并設計AFSA對算例進行求解,運行了多組仿真實驗。結果表明,考慮地震沖擊的貨位分配方法不僅不會使分配結果保守,而且還提高了貨架的穩定性,同時減少客戶訂單的揀選距離,從而提高倉儲作業效率。