GM(1,N)模型的病態(tài)性研究及其在生態(tài)創(chuàng)新中的應用

熊萍萍, 李田田, 檀成偉, 武彧睿

(1.南京信息工程大學 風險治理與應急決策研究院,江蘇 南京 210044; 2.南京信息工程大學 氣象災害預報預警與評估協(xié)同創(chuàng)新中心,江蘇 南京 210044; 3.南京信息工程大學 管理工程學院,江蘇 南京 210044; 4.南京信息工程大學 數學與統(tǒng)計學院,江蘇 南京 210044)

0 引言

習近平總書記在二十大報告中明確指出,“創(chuàng)新是第一動力,創(chuàng)新驅動發(fā)展戰(zhàn)略,堅持創(chuàng)新在我國現代化建設全局中的核心地位”,同時要推動綠色發(fā)展,促進人與自然和諧共生,表明了國家對綠色發(fā)展、生態(tài)文明建設的堅定信念。工業(yè)企業(yè)是實施技術創(chuàng)新向生態(tài)創(chuàng)新轉化的最主要行動者。由于生態(tài)創(chuàng)新多投入和短期效果不明顯,嚴重阻礙了生態(tài)創(chuàng)新的發(fā)展。因此,生態(tài)創(chuàng)新相關指標的數據量有限,企業(yè)生態(tài)創(chuàng)新系統(tǒng)結構復雜,具有一定的不確定性、貧信息等特征。

鄧聚龍教授針對小樣本數據特征創(chuàng)立了灰色系統(tǒng)理論。其中離散GM(1,1)模型建模時的病態(tài)性會導致模型的不穩(wěn)定性,便運用向量的數乘和旋轉變換將矩陣轉化為良態(tài)矩陣[1]。針對病態(tài)性問題的研究還有利用數乘變換解決了引入累積法對模型參數估計時產生的病態(tài)問題[2],以矩陣譜條件數研究灰色Verhulst擴展模型的病態(tài)性[3],基于矩陣求逆的條件數探討GM(1,1)冪模型的病態(tài)性[4]。

GM(1,N)模型包含一個系統(tǒng)特征變量和N-1個影響因素變量,但該模型在建模機理、參數求解和模型結構方面存在缺陷,故學者對GM(1,N)進行了優(yōu)化。對具有卷積積分的GM(1,N)模型賦予新的權重,提出新信息優(yōu)先積累方法改變模型結構[5];考慮系統(tǒng)行為變量和相關變量可能存在非線性關系,引入非線性參數,如基于核函數提出的非線性KGM(1,N)模型[6],基于伯努利方程提出的灰色伯努利NGBM(1,1,k,c)模型[7]等,這些模型的基本思想都是引入非線性公式,將其轉化為線性形式,再建立多元灰色模型。參數求解方面,在GM(1,N)模型的驅動項上引用冪指數,建立了GM(1,N)冪模型,采用智能優(yōu)化算法求解冪指數和對模型進行參數估計[8]。此后也將GM(1,N)模型從實數序列拓展到灰數序列用于預測[9]。

GM(1,N)模型在進行建模時,需要滿足各影響因素之間相互獨立才能確保模型的建模效果合理。然而在實際應用中,影響因素之間多存在一定的相關性,導致在利用普通最小二乘法對模型進行求解時,協(xié)方差矩陣因接近奇異而使得模型的解出現過擬合的現象。這種情況下,我們將它認為模型出現了病態(tài)性。然而在現有的研究中,針對GM(1,N)模型病態(tài)性問題的改進仍存在不足。本文由此提出基于L2范數的最小二乘法,對模型的參數估計進行優(yōu)化,以此解決模型求解時面臨的病態(tài)性問題。為了彌補參數缺陷,由差分方程直接進行參數估計和求解時間響應式,從而確保參數應用的同源性。對GM(1,N)模型的建模進行優(yōu)化以后,進行案例分析,將該模型應用到工業(yè)企業(yè)專利數的預測中,通過實例分析,進一步驗證本文優(yōu)化模型的合理性和有效性。

1 GM(1,N)模型

(1)

為GM(1,N)模型。

2 帶L2正則項的GM(1,N)模型的建模機理

由于灰色預測模型GM(1,N)針對小樣本數據進行擬合,在面臨變量個數多于樣本個數問題或者影響因素間存在強關聯(lián)性時,使用最小二乘法進行參數求解,可能會出現矩陣BTB奇異化,導致參數列解的不穩(wěn)定。所以本文提出引入L2正則項的最小二乘法進行參數估計,其算法原理是在殘差平方和函數上增加L2正則項,通過最小化所有系數達到目的,以此解決模型求解的病態(tài)性問題。

2.1 基于優(yōu)化算法的GM(1,N)模型的參數估計

2.1.1 帶L2正則項的最小二乘法

2.1.2 帶L2正則項的最小二乘法的性質

探討引入L2正則項的最小二乘法對GM(1,N)模型進行參數估計的性質。

從性質1至性質3出發(fā)可以得到,模型的參數估計雖然失去了普通最小二乘法的無偏性,但合適的正則項系數能夠有效的解決模型參數估計時均方誤差較大的問題,使得模型的估計更加的穩(wěn)定、合理。同時也驗證了基于L2范數約束的最小二乘法,能夠解決模型估計時存在的病態(tài)性問題。

2.2 帶L2正則項的GM(1,N)模型的解

本文將直接通過構造模型的方程來得到參數估計和時間響應式,這樣就可以確保參數估計與參數應用的同源性。

定理3GM(1,N)模型如式(1)所述,則

(i)當k=2,3,…,n時,模型的時間響應式為

(ii)當k=2,3,…,n時,模型的累減還原式為

(4)

2.3 參數λ的確定

2.4 模型的精度檢驗

(5)

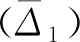
(6)

(7)

模型擬合和預測的精度高低是衡量所構建模型好壞的重要標準,規(guī)定當模型平均相對擬合誤差和平均相對預測誤差均小于10%,則稱構建的模型通過誤差檢驗。

3 實例分析

3.1 江蘇省工業(yè)企業(yè)專利數預測

3.1.1 變量的選取

本文采用工業(yè)企業(yè)專利數作為生態(tài)創(chuàng)新的衡量指標[11]。由于生態(tài)創(chuàng)新的發(fā)展受到經濟發(fā)展水平[12]、政策扶持力度[13]等多方面的影響,因此考慮了多個因素對其產生的影響,以期能更好地預測工業(yè)企業(yè)專利數。

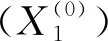
3.1.2 模型的建立

步驟1根據選定的數據,計算系統(tǒng)行為變量與影響因素變量之間的灰色絕對關聯(lián)度,結果如下:

ε12=0.68,ε13=0.69,ε14=0.62,ε15=0.67,ε16=0.64

步驟3構建GM(1,6)模型。根據定理3,得到GM(1,6)模型為

步驟4計算優(yōu)化模型與對比模型的模擬值和平均相對誤差,結果如表1。

表1 灰色模型比較

由表1可以看出優(yōu)化的GM(1,6)模型的平均相對模擬誤差是6.412%,平均相對預測誤差是6.445%,且均小于10%,說明模型的模擬精度和預測精度都高,模型建立合理。

3.1.3 模型比較

(1)優(yōu)化灰色預測模型與其他灰色預測模型比較

將不同算法的灰色模型進行比較,三種方法的預測結果,如圖1所示。

圖1 預測模型比較

通過圖1看出傳統(tǒng)算法的GM(1,6)模型預測結果與真實值相差過大。 GM(1,1)模型的平均相對模擬誤差和平均相對預測誤差分別為3.59%和12.887%。三種預測方法中,雖然GM(1,1)模型的模擬效果比改進算法的模型好,但是預測誤差大于10%,其次GM(1,1)模型只根據工業(yè)企業(yè)有效發(fā)明專利數這個指標進行模擬預測,沒有充分考慮其他因素對其產生的影響,而優(yōu)化算法的GM(1,6)模型無論是模擬誤差還是預測誤差均低于10%,且將各方面的影響因素考慮進其中。

(2)優(yōu)化模型與統(tǒng)計模型比較

將江蘇省規(guī)模以上工業(yè)企業(yè)有效發(fā)明專利數(件)作為因變量,規(guī)模以上工業(yè)企業(yè)開發(fā)新產品經費(萬元)、地方財政科學技術支出(億元)、城市污水日處理能力(萬立方米)、地區(qū)生產總值(億元)和規(guī)模以上工業(yè)企業(yè)流動資產合計(億元)作為自變量,建立多元回歸模型。由R軟件得出的回歸結果知:這五個自變量與規(guī)模以上工業(yè)企業(yè)有效發(fā)明專利數之間的相關系數都大于0.9,由此認為它們之間存在高度相關,說明自變量對因變量存在影響,故建立多元線性回歸模型。

選取我院2016年1月～2018年1月收治的100例冠心病患者，所有患者年齡均超過60周歲，分介入組和藥物組，各50例。藥物組：男24例、女26例，年齡62～80歲，平均72.8±5.4歲；介入組：男26例、女24例，年齡60～78歲，平均70.8±6.4歲。兩組患者的一般資料，無統(tǒng)計學差異性。

在顯著性水平α=0.05下,得到F值為77.75,大于臨界值Fα(5,4)=6.26,通過顯著性檢驗,說明因變量與自變量之間存在線性關系。接著對各回歸系數分別進行t檢驗,以判斷每個自變量對因變量的影響是否顯著。所有的自變量均未通過檢驗,說明多元回歸建立是不合理的。計算得自變量的方差擴大因子VIF大于10,說明多元回歸模型存在嚴重的多重共線性,故使用嶺回歸建模。

嶺回歸結果顯示,當k值較小時,參數列的值很不穩(wěn)定,當k值逐漸增大時,各參數趨于零,此時選擇k值為0.04,各參數值基本上都能相對穩(wěn)定。并將模擬結果和預測結果與灰色預測模型比較,比較結果如表2所示。

表2 灰色預測模型與統(tǒng)計模型比較

由表2得出嶺回歸模型的平均相對模擬誤差為4.795%,平均相對預測誤差為7.346%。它的模擬效果優(yōu)于基于優(yōu)化算法的GM(1,6)模型,但是預測效果不及基于優(yōu)化算法的GM(1,6)模型。而且生態(tài)創(chuàng)新具有樣本量少,影響因素結構復雜導致不確定性等灰色特征,故使用灰色預測模型進行模擬預測更具有實際意義。

由此可以看出灰色模型預測效果更好。統(tǒng)計模型是基于概率統(tǒng)計基礎上進行回歸預測的,一般來說,樣本數量越大,得到的預測效果越好,而針對于小樣本數據,統(tǒng)計模型獲得的有用信息少,所以導致預測效果不好,此時更適合選擇灰色模型進行預測。根據基于優(yōu)化算法的GM(1,6)模型的結果來看,江蘇省規(guī)模以上工業(yè)企業(yè)有效發(fā)明專利數呈指數遞增趨勢,其中地方財政科學技術支出和規(guī)模以上工業(yè)企業(yè)流動資產合計對生態(tài)創(chuàng)新的發(fā)展起到了更重要的影響作用。

3.2 華北地區(qū)工業(yè)企業(yè)專利數預測

3.2.1 變量的選取

本實例選取來自國家統(tǒng)計局2011～2019年的華北五省工業(yè)企業(yè)有效發(fā)明專利數,采用華北地區(qū)規(guī)模以上工業(yè)企業(yè)有效發(fā)明專利數(件)作為系統(tǒng)行為變量。以規(guī)模以上工業(yè)企業(yè)單位數(個)、供水綜合生產能力(萬立方米/日)、城市污水日處理能力(萬立方米)、工業(yè)污染治理完成投資(萬元)和規(guī)模以上工業(yè)企業(yè)R&D人員全時當量(人年)為相關影響因素指標,將2011～2017年的數據為訓練集,2018～2019年數據為測試集。

3.2.2 模型的結果比較

基于優(yōu)化算法的GM(1,6)模型的平均相對模擬誤差是7.598%,平均相對預測誤差是1.778%。說明模型的模擬和預測精度都高,模型建立合理。將基于優(yōu)化算法的GM(1,6)模型與傳統(tǒng)算法的GM(1,6)模型、GM(1,1)模型和嶺回歸模型進行比較,為了更加直觀描述各個模型的建模效果,對比結果如圖2所示。

圖2 模型結果比較

從圖2可以得出GM(1,6)傳統(tǒng)算法的解不穩(wěn)定,其模擬和預測效果都偏離真實值,與原序列的發(fā)展趨勢相違背,從而驗證了若模型求解存在病態(tài)性,使用傳統(tǒng)算法求解的結果并不具備參考價值。預測模型GM(1,1)的平均相對模擬誤差為2.906%,平均相對預測誤差為15.770%,雖然模擬效果較好,但是預測誤差大于10%,沒有通過模型的誤差檢驗。而基于優(yōu)化算法的GM(1,6)模型,無論從模擬效果還是預測效果,都通過了誤差檢驗,并且得出的解具有穩(wěn)定性,解決了模型求解的病態(tài)性問題。統(tǒng)計模型嶺回歸的平均相對模擬誤差為15.025%,平均相對預測誤差為35.059%,模擬和預測效果都不如本文提出的灰色預測模型效果好,這也證實了對于具有灰色特征的數據,使用灰色模型進行預測,效果更好。

4 結論

傳統(tǒng)算法的GM(1,N)模型具有參數應用缺陷和病態(tài)性問題,本文通過引入L2正則項的最小二乘法進行參數估計,有效的解決了病態(tài)性問題。由模型的差分方程直接得到時間響應式和參數求解,從而保證了參數來源的統(tǒng)一性,避免了參數缺陷。將優(yōu)化算法的模型運用到生態(tài)創(chuàng)新數據中,并將結果與其它灰色預測模型和統(tǒng)計模型進行比較,結果表明,優(yōu)化算法后的模型模擬和預測誤差通過精度檢驗,且預測結果具有參考價值。在小樣本數據下,灰色模型的預測性能優(yōu)于回歸模型,從而驗證了灰色模型適用于小樣本、具有灰色特點的數據,能夠更好地進行預測。這不僅豐富了灰色預測模型的理論體系,也為生態(tài)創(chuàng)新相關指標預測提供了新的方法。

本文仍存在一定的不足之處。在對正則項系數進行確定時,本文偏好性地利用了粒子群算法在擬合誤差最小的條件下確定了相對最優(yōu)的正則項系數值,使得模型的參數估計更加合理,以此消除了模型的病態(tài)性問題。但在該算法下確定正則項系數未必對所有的實際應用都可行,可能出現建模效果不佳。因此,讀者還可以從均方誤差最小準則或者絕對誤差最小準則出發(fā),選擇其它優(yōu)化算法找到模型的相對最優(yōu)正則項系數值,以解決模型的病態(tài)性問題。