基于組合模型的股指價格短期預測

關永鋒, 喻 敏

(1.武漢科技大學 冶金工業過程系統科學湖北省重點實驗室,湖北 武漢 430081; 2.武漢科技大學 理學院,湖北 武漢 430065)

0 引言

作為反映一個國家宏觀經濟狀況的“晴雨表”,股指價格的變化直接影響金融市場的穩定以及國民經濟的發展。準確的預測模型可以為金融市場的決策提供依據,但是,受經濟、政治等因素的影響,股指數據呈現出高度波動的特征,因此,在金融市場中找到一個穩健的股指價格預測方案是一項困難和具有挑戰性的任務[1～3]。

目前,常用的預測方法包括時間序列分析模型[4,5]、神經網絡算法[6,7]、支持向量機[8,9]等。時間序列分析常用模型為自回歸移動平均模型(Auto-Regressive Moving Average model, ARMA),其使用前提是序列必須為平穩的,強行將其用于不平穩數據的預測往往會出現“偽回歸”現象;反向傳播神經網絡(Back Propagation network, BP)運用誤差反向傳播的思想,彌補了多層神經網絡參數學習問題,但容易陷入局部最優;支持向量機模型常用于小樣本建模預測,能較好的獲取全局最優,但是該算法需要設定的參數過多,缺少使得多個參數同時達到最優的選擇方案。

股指價格數據具有非線性、非平穩的特征,在對其進行預測前常常需要經過平穩化、線性化處理,常用的預處理手段包括小波分解[10]、經驗模態分解[11,12]等。小波分解算法需面臨小波基函數的選擇問題,目前尚無統一的選擇標準可供參考;經驗模態分解算法則從數據自身出發進行自適應分解,無需進行參數的選擇,但當原始數據含有較多噪音時,其分解出來的分量會出現模態混疊現象,使EMD分解結果無法表示真實的物理過程。

針對上述問題,本文從兩方面入手改進,在預處理手段上,采用改進的經驗模態分解算法(HF-EMD)對股指數據進行自適應分解,該算法在信號分解、故障檢測[13,14]等領域的應用中取得了良好的效果,能有效改善EMD算法所產生的模態混疊現象;在預測模型的選擇上,采用粒子群優化后的極限學習機模型(PSO-ELM)對分解后的各子序列進行預測,與傳統的人工神經網絡模型相比,ELM模型具有更快的學習速度,在非線性含噪數據的擬合中有較好的效果,在引入PSO算法進行優化后,模型整體的預測精度與魯棒性也得到了進一步提高。最后,將各分量的預測值進行等權加和獲得最終的預測值。以上證指數、日經225指數、恒生指數、標普500指數為代表的四組國內外股指數據進行的仿真實驗表明,該組合模型在股指價格短期預測中具有較好的效果。

1 算法與模型

1.1 EMD算法

經驗模態分解是由HUANG等[15]提出的一種用于處理非線性非平穩信號的方法,不同于傅里葉變換、小波變換等傳統的時頻分析方法,它不需進行基函數的選擇,而是從信號自身出發進行自適應分解,具有很好的時頻聚集性。

EMD算法可以將原始信號分解為一組本征模態函數(Intrinsic Mode Functions, IMF),每一個IMF反映了不同的頻率特征。本征模態函數需要滿足以下兩個特征:

1)在IMF定義域中,極值點個數與零點個數要相等,或二者相差值不超過1;

2)由局部極大值和局部極小值形成的上下包絡函數的和要恒為0。

當原始信號為x(t)時,EMD算法的分解流程如下:

1)由x(t)確定全部的局部極大值和局部極小值;

2)用三次樣條曲線分別連接所有極大值和極小值,形成上包絡線xu(t)和下包絡線xd(t);二者的均值為m1(t);令差值為h1(t)=x(t)-m1(t),驗證h1(t)是否滿足IMF的兩個條件。若滿足,則h1(t)為第一個IMF分量;若不滿足,則用h1(t)替代原始信號x(t),并重復上述步驟,直到滿足IMF的兩個條件,得到第一個IMF分量;

3)令余項為r1(t)=x(t)-h1(t),用r1(t)替換掉原始信號x(t),對上述三個步驟進行迭代,得到后續的分量,直到最后一個分量hn(t)產生的余項rn(t)小于某一特定值或為一個單調函數時,EMD分解過程結束。

最終,原始信號x(t)可以表示為各IMF分量及余項rn(t)的等權加和。

1.2 改進的EMD算法

EMD算法的分解過程很大程度依賴于原始信號極值點的選取,而股指數據受外界各種因素的影響常常會出現極為強烈的波動,導致其極值點分布不均勻,若強行對其進行EMD分解,會出現模態混疊的現象,大大降低分解效果。但是,在股指價格的預測當中,前人大都直接使用EMD分解方法對股指數據進行分解[11,12]。在此,本文首次將高頻諧波抑制EMD算法模態混疊現象的方法應用到股指數據的預處理過程當中。該算法的思路是在EMD分解之前往原始信號中注入適當的高頻信號,改變原始信號的極值分布,減弱或“淹沒”引起模態混疊現象的高頻短時擾動成份,從而使信號包絡更自然,減小分解誤差,優化EMD算法的分解效果。

對股指價格數據進行實驗測試后,發現加入高頻正弦諧波信號的頻率為原始信號采樣頻率的1/3倍時,EMD分解出來的IMF分量更平穩,且頻率尺度較低的分量的軸對稱也更明顯,能有效減少模態混疊現象。因此,本文選取幅值為未加入高頻信號EMD分解的第一層分量IMF1的平均幅值,頻率為1000Hz的正弦諧波信號。具體地,將該高頻信號注入上證指數日收盤價序列后進行EMD分解,從分解出來的第一層分量中減掉高頻諧波,分解結果如圖1所示。未加入高頻信號的EMD分解結果如圖2所示。圖中HF-EMD分解出來的IMF6與EMD分解出來的IMF7相對應,可看出注入高頻諧波的EMD分解結果更平穩,并且該分量軸對稱性也更明顯。其他的分量也存在類似的改善。此外,HF-EMD的分解層數也減少了一層,這有利于減少預測模型的計算量,加快預測速度。

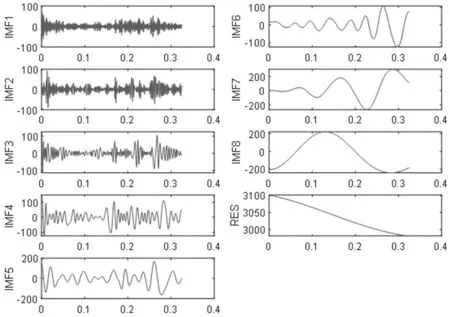
圖2 EMD算法的分解結果

1.3 粒子群優化的極限學習機模型

神經網絡模型對非線性數據具有較好的擬合效果,常用于股指價格的預測當中[6,7]。極限學習機是基于單隱含層前饋神經網絡的一種改進算法,具有學習速度快、泛化能力較好等優點,能克服傳統神經網絡模型訓練速度慢、易陷入局部最優等缺點。

設有M個不同的隨機樣本(xi,yi)∈Rn。若網絡的隱含層神經元個數為L,激活函數為g(x),隱含層第i個節點的輸入權值向量為wi,偏置值為bi,輸出權值向量為βi,于是SLFN模型可表示為:

(1)

式中,j=1,2,…,M。

依據零誤差逼近原則,上述模型能無限逼近M個訓練樣本,存在βi、wi和bi使得下式成立

(2)

式中,j=1,2,…,M。

對應的矩陣形式為:

Hβ=YT

(3)

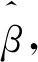
式中,H+為隱含層輸出矩陣H的Moore-Penrose廣義逆矩陣。

粒子群優化算法是一種群智能優化算法,基于“種群”和“進化”的概念,通過個體間的協作與競爭,實現復雜空間最優解的搜索。而ELM模型初始的輸入層與隱含層間的連接權值w,隱含層的偏置值b是隨機產生的,為減小初始的隨機設定所帶來的偏差,增加ELM網絡的穩定性,本文提出采用粒子群算法優化ELM的初始權值和偏置值。以上證指數日收盤價數據為例對該算法具體步驟的說明如下:

1)確定PSO-ELM模型的拓補結構。采用迭代尋優的方法確定網絡的隱含層神經元個數,而網絡的輸出維數為1,激活函數選擇的是Sigmoid函數;

2)粒子群的初始化及更新。本文的種群由ELM的輸入層-隱含層的權值w,隱含層的偏置值b組成,群體規模N為10,最大迭代次數為50,粒子維數D為39;粒子速度最大值為1,最小值為-1;粒子位置最大值為5,最小值為-5;學習因子c1、c2均為1.5;以ELM訓練集的輸出誤差作為適度值函數,計算出每個粒子的適度值fiti;將每個粒子的適度值fiti分別與個體極值pbest、全局極值gbest作比較,若適度值fiti更小,則可用其替換掉個體極值pbest和全局極值gbest;而后,通過迭代來更新每個粒子的速度和位置;

3)判斷是否達到最大迭代次數或最小誤差,若達到則停止,否則繼續。

1.4 基于HF-EMD-PSO-ELM的短期預測組合模型

由于股指價格是一類具有非平穩性、非線性性的數據,使用單一模型對其進行預測很難捕獲隱藏在原始數據中的所有信息,缺乏數據平穩化處理的過程,而采用多尺度分解算法與單一模型相結合的組合預測[16,17]能獲得更好的效果。組合預測模型的思想是從不同角度獲取數據的變化信息,集成單一預測模型的優點,避免單一模型預測過程中的誤差累積。本文遵循“分解-組合”的思想,提出一種基于HF-EMD以PSO-ELM的股指數據預測模型,如圖3所示,該模型的預測流程如下:

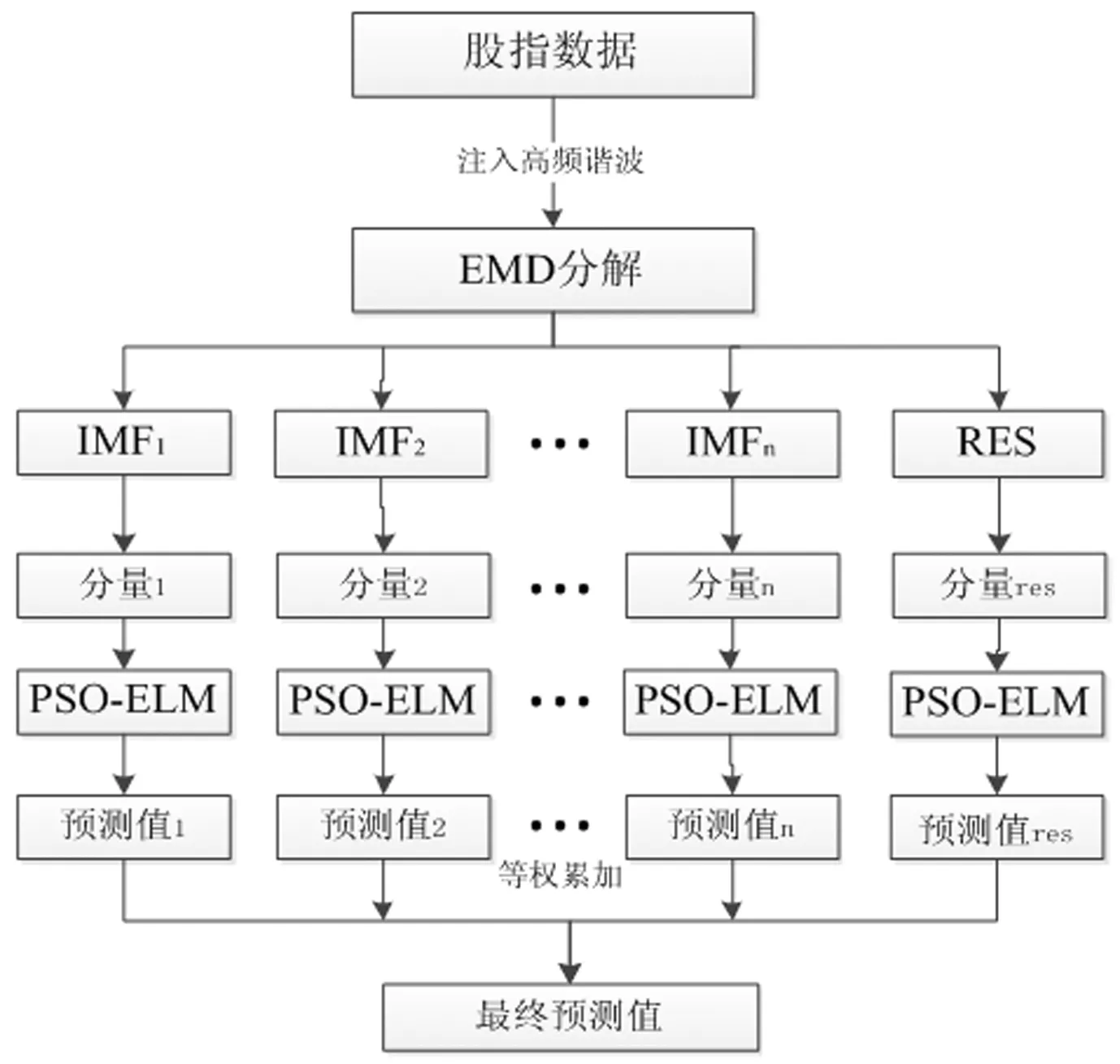
圖3 本文模型的預測流程

1)向股指價格數據中注入高頻諧波,利用EMD算法對其進行分解,獲得若干個含不同頻率成分的IMF分量,對每個分量數據區分訓練集和測試集,并進行歸一化處理;

2)對各IMF分量采用PSO-ELM模型依次進行預測,獲得各分量預測值;

3)等權累加各分量的預測值獲得最終的股指價格預測值。

1.5 指標評價及模型檢驗

為說明本文模型對于股指價格的預測效果,選取平均絕對誤差(Mean Squared Error,MAE)平均絕對百分比誤差(Mean Absolute Percentage Error, MAPE)、均方根誤差(Root Mean Square Error, RMSE)這三個指標對模型的預測性能進行評價。計算公式如下:

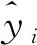
同時,引入Diebold-Mariano(DM)檢驗用于測試每個模型的殘差序列間是否存在顯著差異。

2 實證分析

2.1 樣本選取和評價指標

本文選取2016.01.01～2019.12.31期間,以上證指數、日經225指數、恒生指數、標普500指數為代表的四組國內外股指指數的日收盤價進行實驗分析。由于各國對于股指數據的統計方法存在差異,因此所獲取的四組數據的樣本數據量不盡相同,在此取各組數據的后100個數據作為測試樣本,剩余的數據作為訓練樣本。圖4給出了四支股票日收盤價的走勢圖,可看出這些序列存在明顯的非線性性及波動性。

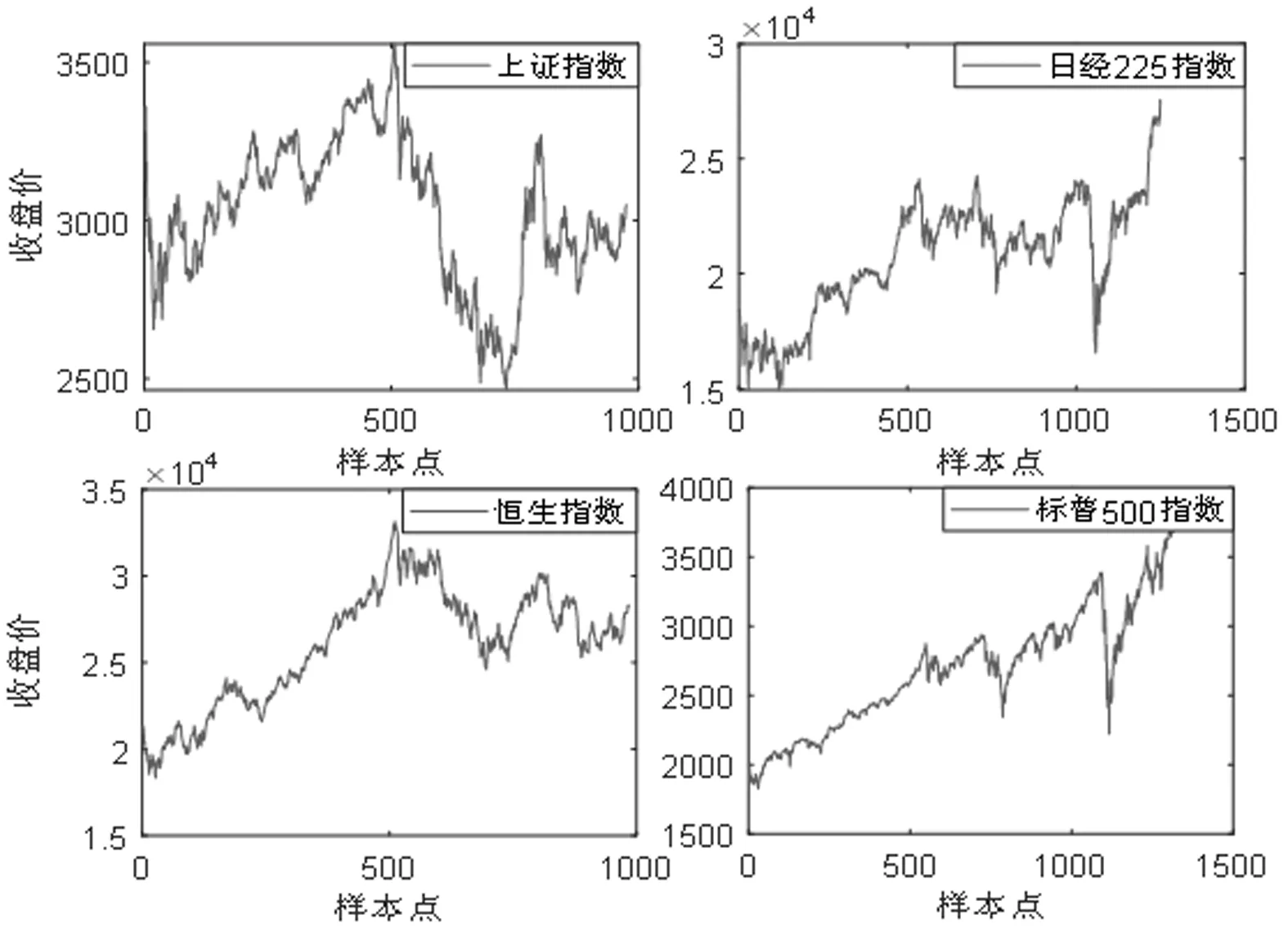
圖4 各支股票收盤價走勢

2.2 實驗分析及對比

為說明本文所提組合模型的預測效果,選取ARMA、BP、ELM、PSO-ELM為單一基準模型,EMD-PSO-ELM為組合基準模型,與本文模型進行對比。各模型預測結果如圖5～圖8所示,表1為各模型評價指標的結果。

表1 各模型預測結果比較

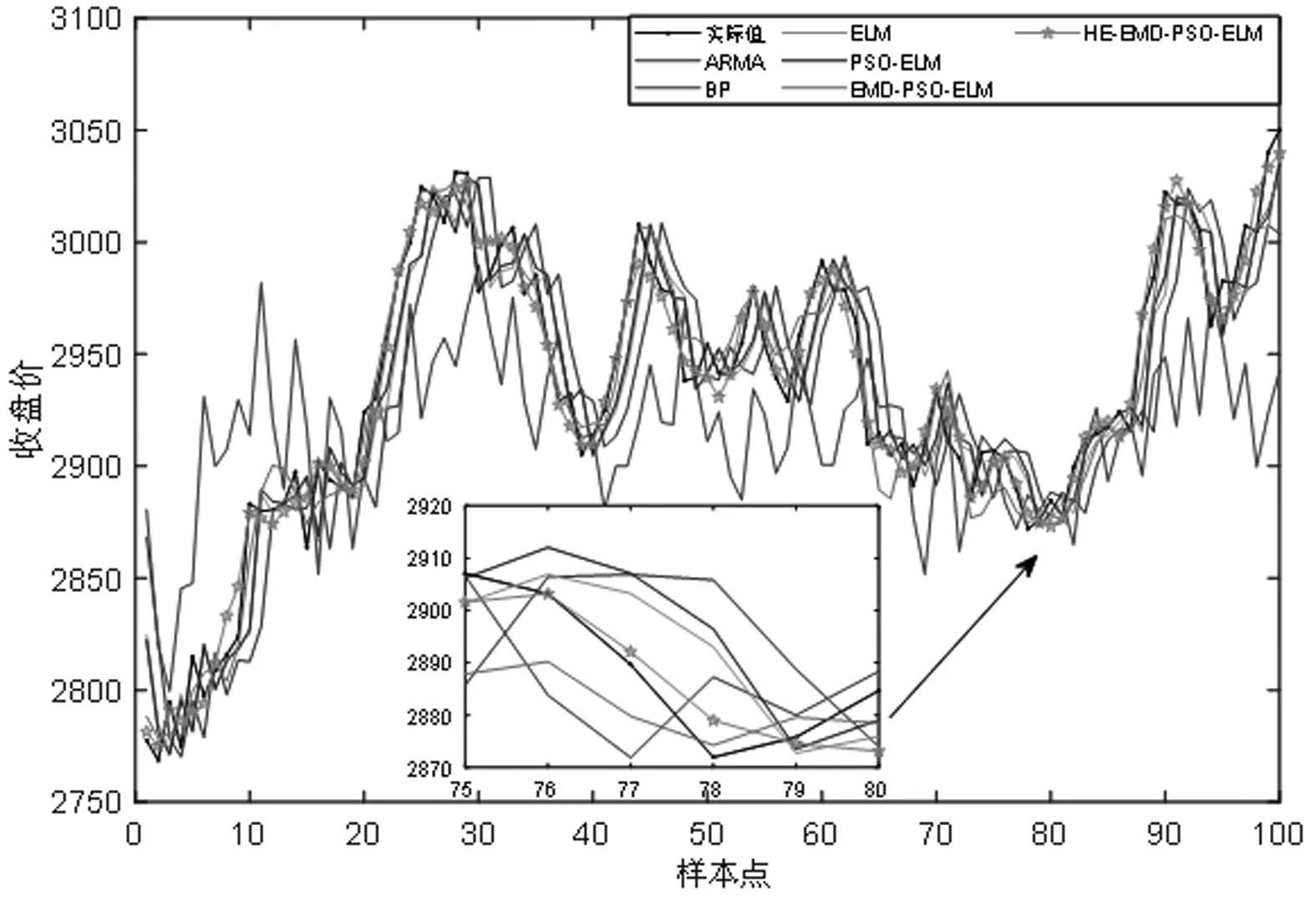
圖5 上證指數各模型預測效果

圖6 日經225指數各模型預測效果

圖7 恒生指數各模型預測效果

圖8 標普500指數各模型預測效果

從單一模型的角度來看,與ARMA、BP、ELM模型相比,PSO-ELM具有更好的預測效果。以上證指數為例,優化后的ELM模型MAE值為16.2377,相較于其他單一模型中預測效果較好的ELM模型而言,降低了3.77%,其他指標MAPE、RMSE也有顯著的改善,這說明結合了ELM模型學習速度快及PSO啟發式全局尋優兩個優點的PSO-ELM模型能有效提高股指價格數據的預測精度。

從組合模型的角度看,本文模型與組合基準模型的預測效果均高于單一基準模型,這說明引入了多尺度分解手段對股指數據進行預處理后,能有效降低數據的非平穩性,顯著提高模型的預測精度。以恒生指數為例,本文模型的MAPE值為35.10%,相較于單一模型中預測性能較好的PSO-ELM模型而言,降低了35.81%,降幅達到了50.50%,其他指標MAE、RMSE也有顯著的改善。進一步比較兩種組合模型的預測精度,可發現HF-EMD-PSO-ELM模型具有更好的預測效果,以標普500指數為例,本文模型的RMSE為16.0382,相較EMD-PSO-ELM模型而言,降低了3.8444,降幅為19.34%,其他指標MAPE、MAE也呈現出相似的結果。可見,在引入了高頻諧波對EMD算法進行改進后,能有效緩解模態混疊現象,有利于把握股指數據的變化規律。

最后,采用Diebold-Mariano檢驗對各模型的有效性進行檢驗,將本文提出的HF-EMD-PSO-ELM模型的殘差序列與其余5類基準模型的殘差序列分別進行DM檢驗,結果如表2所示。由表可知,在1%的置信水平下,本文模型與單一基準模型的預測精度具有明顯差異;在5%的置信水平下,本文模型與組合基準模型的預測精度具有明顯差異。

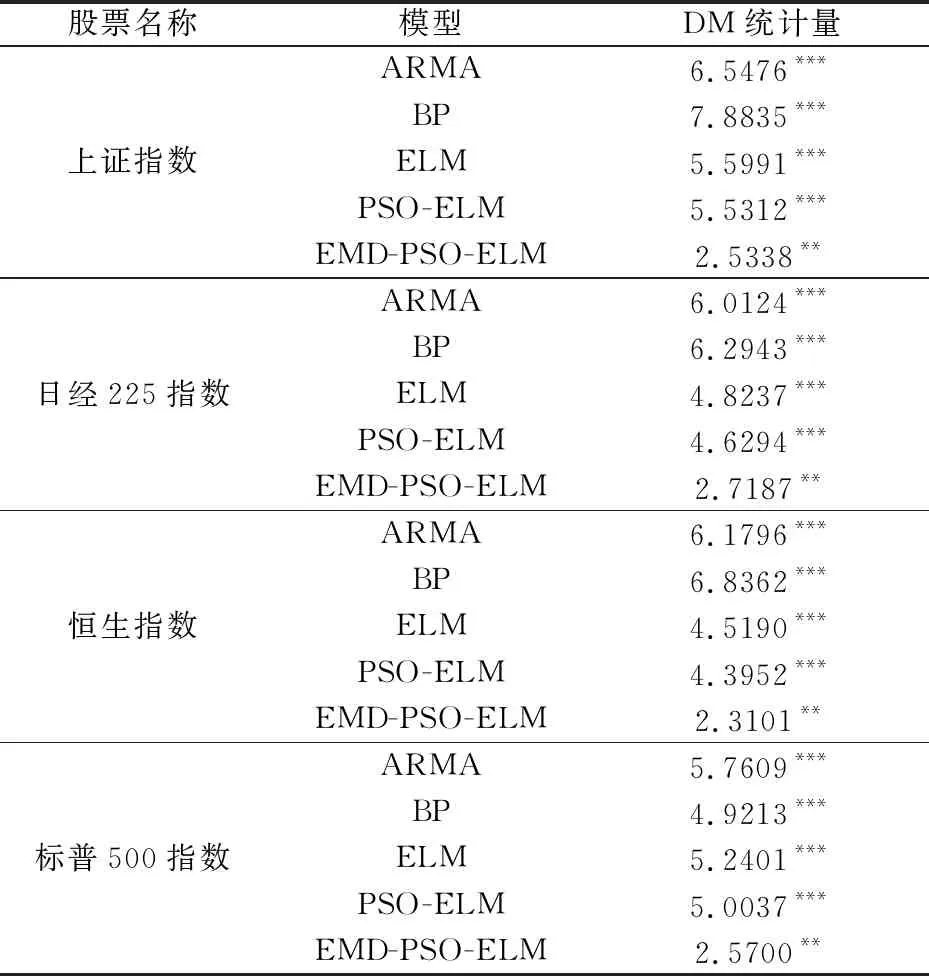
表2 各模型與HF-EMD-PSO-ELM模型的DM檢驗結果

綜上,由于股指價格的波動呈現出復雜的非線性關系,在使用傳統分解方法獲取股指價格的高頻擾動及長期趨勢時會產生模態混疊,利用高頻諧波改變原始股指價格序列的極值分布再進行經驗模態分解,有利于準確提取不同分量的波動特征。同時,利用PSO-ELM模型對各模態分量進行組合預測,能準確反映股指價格的漲跌情況,為投資者的決策提供依據。因此,與傳統預測模型相比,本文所提模型能準確把握股指價格的變化規律,有效提高預測的準確性與魯棒性。

3 結論

本文基于改進的EMD算法和PSO優化的ELM模型,針對股指價格數據非平穩非線性的特征,提出了一種用于股指價格短期預測的組合模型。對近4年國內外四組具有代表性的股指數據進行實證分析,得出以下結論:

1)利用多尺度分解的方法對股指價格數據進行預處理后,能有效提高模型的預測精度。將原數據分解為不同頻帶的分量后,不僅解決了原數據非線性非平穩的問題,而且還豐富了預測數值的經濟含義。同時,將多尺度分解方法與群智能優化算法引入單一模型的改進后,能顯著提高股指價格的預測精度,有效避免單一模型在預測過程中的誤差累積。

2)利用高頻注入法的改進EMD算法(HF-EMD)對股指數據進行分解,能有效改善在僅使用EMD分解時所產生的模態混疊現象,各分量更平穩且軸對稱性更好。同時,注入高頻后,EMD分解的分量個數有所減少,可減少后續預測的計算量。該方法為股指數據預處理提供了一種新的思路。