Filippov系統的邊界平衡點分岔

曹南斌 呂志敏

【摘? ?要】? ?對一類Filippov系統的邊界平衡點分岔進行分析，并證明Filippov系統發生邊界平衡點分岔的條件，最后呈現Filippov系統對應的分岔圖。

【關鍵詞】? ?Filippov系統；邊界平衡點分岔；分岔圖

Boundary Equilibrium Bifurcation of Filippov Systems

Cao Nanbin， Lv Zhimin

（ Hebei GEO University， Shijiazhuang 050031， China）

【Abstract】? ? In this paper， the stability of equilibrium point and boundary equilibrium bifurcation of a class of Filippov systems is studied， and the paper proves the condition for the existence of boundary equilibrium bifurcation of Filippov systems. Finally， the paper presents the corresponding bifurcation diagrams by numerical simulation.

【Key words】? ? ?Filippov systems; boundary equilibrium bifurcation; bifurcation diagram

〔中圖分類號〕? ?O152? ? ? ? ? ? ? ? ?〔文獻標識碼〕? A ? ? ? ? ? ? ?〔文章編號〕 1674 - 3229（2023）01- 0013- 03

2? ? ?分岔圖

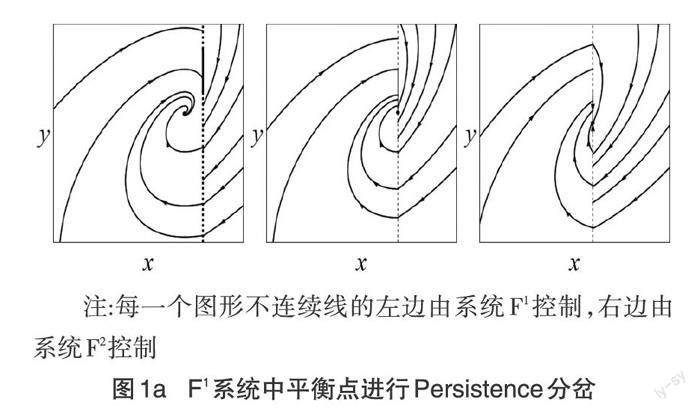
在[p=1，b1=1]情形下對系統（2）進行數值模擬。當[b2=2]時，隨著不連續邊界的移動，可得系統F1的平衡點與不連續邊界發生碰撞，產生偽平衡點，這樣的分岔稱為Persistence分岔，見圖1a。系統F2的平衡點和一個存在的偽平衡點與不連續邊界發生碰撞，最后都消失了，這樣的分岔稱為Non-smooth fold分岔，見圖1b。當[b2=0]時，系統F1與系統F2隨著不連續邊界的移動，出現一族偽平衡點，最后都消失，這樣的分岔稱為退化分岔。在這一部分僅僅給出了系統F1的分岔圖，見圖2。當[b2=-2]時，隨著不連續邊界的移動，系統F1中的平衡點和偽平衡點與不連續邊界發生碰撞，最后兩類平衡點都消失，這樣的分岔稱為Non-smooth fold分岔，見圖3a。系統F2中的平衡點與不連續邊界發生碰撞變成邊界平衡點，最后變成偽平衡點，這樣的分岔稱為 Persistence 分岔，見圖3b。

3? ? ?結語

本文給出了一類具有一條變化不連續邊界的Filippov系統，討論了系統的邊界平衡點分岔。

［參考文獻］

［1］ Giannakopoulos F， Pliete K. Planar systems of piecewise linear differential equations with a line of discontinuity［J］. Nonlinearity， 2001， 14（6）： 1611.

［2］Bernardo M， Budd C， Champneys A R， et al. Piecewise-smooth dynamical systems： theory and applications［M］. Springer Science Business Media， 2008.

［3］ Kuznetsov Y A ， Rinaldi S ， Gragnani A . One-Parameter Bifurcations in Planar Filippov Systems［J］.INTERNATIONAL JOURNAL OF BIFURCATION AND CHAOS，2003， 13（8）：2157-2188.

［4］ Di Bernardo M， Pagano D J， Ponce E. Nonhyperbolic boundary equilibrium bifurcations in planar Filippov systems： a case study approach［J］. International Journal of Bifurcation and chaos， 2008， 18（5）： 1377-1392.