海上火箭回收過程中船舶耦合運動響應分析

王智，劉大輝，王壽軍，滕瑤

(1.哈爾濱工程大學 煙臺研究生院，山東 煙臺 264000；2.中集海洋工程研究院有限公司，山東 煙臺 264670)

0 引言

我國在2019 年于山東煙臺附近海域第一次成功海上火箭發射后，已進行了多次海上火箭發射任務，形成了完整的海上發射體系[1]，為提高商業發射的經濟性，后期將會對發射后的一級火箭進行回收再利用，SpaceX 公司的垂直回收技術使火箭發射成本降低約30%。相比陸地回收，海上火箭回收的經濟性更高，該過程不需供給一級火箭反推回陸地的燃料，可按照火箭的自由運動軌跡進行回收[2]。目前我國海上火箭回收技術處于驗證階段，仍有很多關鍵技術未解決，如回收船舶作業全過程運動響應分析、載荷數值預報技術研究等。

在沖擊載荷作用下的船舶運動響應分析方面，俞俊等[3]基于AQWA 探討了海上火箭冷發射過程中不同工況下平臺的運動問題，將垂向5000 kN 和10000 kN的定常力作為火箭沖擊載荷輸入至Aqwa 中，得出沖擊載荷越大，相同偏心位置下平臺運動極值越大等結論。王建平等[4–5]利用KANE 方法數值求解了在艦載火炮系統橫向力作用下的船舶運動狀態，與實驗數據進行比對，驗證了模型的準確性，并講解了該模型試驗。在火箭海上回收過程中，甲板所受沖擊載荷的動態變化以及系泊系統的耦合作用不可忽略，而上文未考慮此影響。

本文通過建立海上火箭回收過程中船舶的耦合運動分析方法，尋求影響海上火箭回收精度的關鍵因素。以某型火箭發動機及多功能海洋工程駁船為研究對象，基于粘流軟件STAR-CCM+對考慮火箭回落過程的沖擊流場進行模擬，并將所得的沖擊載荷時歷曲線作為輸入導到船舶時域耦合運動方程中。最后，使用勢流軟件Aqwa 在時域上分析不同火箭著陸點對耦合作用下船舶運動響應的影響。

1 理論基礎

1.1 垂直燃氣射流沖擊載荷

對于軸對稱沖擊射流，在火箭燃氣射流動力學[6]里，帶傾角的沖擊載荷計算公式為：

式中：re為噴管出口半徑；pe和pa分別為噴管出口壓力和環境壓力；α為氣流流動對中心線的當地傾角；θ為射流軸線與甲板的傾角；噴管出口面積Ae=比熱比 γ為燃氣流的定壓比熱與定容比熱之比，噴管出口馬赫數Mae為速度與聲速之比，根據3 個參數的定義上式可改寫為：

在海上火箭回收最后的垂直降落階段中，射流與甲板的夾角幾乎為90°，將α=0?及θ=90?代入式（2），最終的垂向沖擊載荷計算公式為：

1.2 時域船舶耦合運動方程

在船舶重心處使用質心動量定理、動量矩定理以及線性水動力理論，得到浮體的六自由度頻域運動方程：

式中：x為船舶的六自由度運動響應；M為船舶的質量矩陣；u為附加質量矩陣；C為靜水回復力系數矩陣；k(t?τ)為延遲函數。方程右端F為作用在重心的外力。根據Cummins 脈沖響應法，將船舶運動及波浪力轉化為一系列脈沖運動響應的疊加，并對頻域上的系數進行傅里葉變換，即得到時域內的延遲函數k(t?τ)等[7]，進一步將上式改寫成時域耦合方程：

右端等式中Fw表示浮體的一階和二階波浪力，運用三維勢流理論和面元法可以求解流場的速度勢，在此基礎上使用伯努利方程并在濕面積下積分即得到波浪力。Fm表示系泊力，由懸鏈線理論求解，FT表示回收過程中甲板受到的沖擊載荷，計算公式見式（3）。在已知這些參數后，求解耦合作用下的浮體時域運動方程。

2 模型描述

2.1 火箭燃氣射流模型

2.1.1 幾何模型

使用的噴管根據我國某型火箭發動機噴管實際尺寸簡化而來，噴管的入口和出口直徑均為1524 mm，喉部直徑為381 mm，喉部到出口長度為1572.2 mm，擴張角為45°。參考Space X 進行的多次海上火箭回收，選取海上回收最后一個階段（垂直降落階段）為研究過程。該過程大約開始于20 m 高空[8]，回收船舶的型寬為40 m，由此確定火箭初始時刻的三維計算域，如圖1(a)所示。燃氣射流從頂部噴管向下噴出，撞擊底部擋板之后沿徑向傳遞擴散，待射流穩定后用底部圓形擋板逐漸靠近頂部噴管的過程模擬火箭回落。為提高計算效率，對三維模型進行優化，簡化后的軸對稱模型如圖1(b)所示。

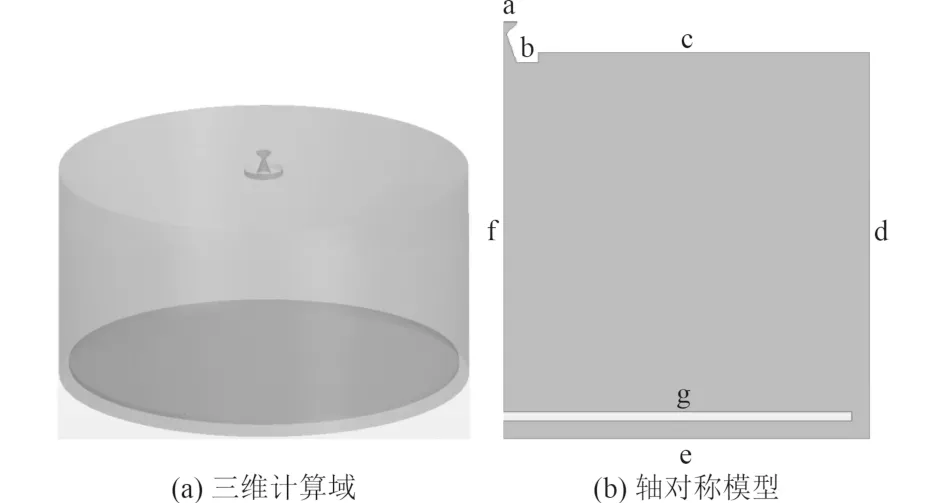
圖1 燃氣射流計算域初始幾何模型Fig.1 Initial geometric model of calculation domain of gas jet

2.1.2 邊界條件

如圖1(b)所示，火箭噴管入口a 采用停滯進口邊界條件。燃燒室總壓為6.08 MPa，入口總溫為3050 K。燃氣射流的出口（用c，d，e 表示）采用壓力出口邊界條件，壓強大小為1 atm，溫度為默認值300 K。與燃氣流相接觸的有甲板面g 和噴管壁面b，均設置為壁面條件，使用標準壁面函數，并采用無滑移絕熱條件。邊界f 設置為軸條件，其他參數設置為默認。

2.1.3 網格條件

模擬過程中對擋板周圍添上重疊網格，并對射流中心區域進行階梯式的網格加密，如圖2所示。劃分后整個流場網格單元數為129984 個，節點數為249542 個，最小體積變化率為0.02，最大體積變化率為1，表面效度為1。

圖2 燃氣射流計算域網格Fig.2 Gas jet computational domain mesh

2.2 海上火箭回收船舶模型

在水動力分析方面，使用的是多功能海洋工程駁船，該船型改良于國內進行過多次海上發射任務的“泰瑞”號，其尺寸滿足實際工程應用的要求。該船的錨泊系統采用多點系泊，為懸鏈線式系泊，系泊系統共有4 根纜繩呈對稱分布，朝著4 個象限的45°方向布置，繩長820 m。船體網格由Aqwa 自動生成，基本網格尺寸為1.6 m，網格總數為13367，船體模型及主要船型如表1 所示。

表1 多功能駁船船體模型及主要參數Tab.1 Hull model and main parameters of multifunctional barge

3 結果與討論

3.1 海上火箭回收過程中燃氣沖擊流場數值模擬

3.1.1 靜態沖擊載荷數值模型驗證

火箭的燃氣沖擊射流是一種高壓、高溫、高速的復雜湍流，包含復雜的流動狀況，對燃氣沖擊射流模擬使用較多的湍流模型是雷諾平均納維-斯托克斯湍流模型(RANS)與大渦模型(LES)，兩者均能反映超音速沖擊射流的主要流動特征[9]。LES 模型更多應用在三維幾何中，RANS 模型則無太多要求。STARCCM+中的RANS 模型有4 種：Spalart-Allmaras 湍流模型對于平面射流和圓柱射流擴散率的計算并不精確；K-Omega 模型對內部流入口邊界條件極端敏感，不適用于高溫高壓入口的燃氣射流模擬。第3 種K-Epsilon 模型則不存在此問題，其中的兩方程Realizablie K-Epsilon 模型是基于標準K-Epsilon 模型的優化，更適合于射流和邊界層流動等。第4 種為雷諾應力傳輸(R S T) 模型，RST 模型因考慮了湍流各向異性和高應變率等影響，對于部分復雜流的模擬可以進行準確預測[10]。

由于參考文獻[11]中并未說明使用的是哪種湍流模型，綜上考慮各個湍流模型的優缺點，選擇RANS模型中的Realizablie K-Epsilon 模型及RST 模型與Nobuyuki Tsuboi等[11]進行的靜態燃氣沖擊射流試驗數據及模擬結果進行比對，試驗使用的噴管尺寸及燃氣參數見文獻[11]。

圖3 為在H=8.74R(H表示噴管出口至地面的距離，R為出口半徑)時，待燃氣射流穩定作用在底面甲板上后，底面甲板徑向上的靜壓比分布(擋板上該點處的靜壓值與環境壓力的比值)曲線。可知，在沖擊射流的中心位置處，Realizable K-Epsilon 模型的結果較其他模型的結果更貼近試驗數據，其在遠離射流中心處的靜壓比分布與試驗結果也貼合得較好。因此在考慮火箭回落過程沖擊載荷的數值模擬中使用Realizable KEpsilon 湍流模型，并將庫朗數設置為自動控制。

圖3 H=8.74R 時擋板上的靜壓比試驗與模擬對比圖Fig.3 Comparison between experiment and simulation of static pressure ratio on baffle when H=8.74R

圖4 H=8.74R 時數值模擬的速度云圖與試驗紋影圖的對比Fig.4 Comparison between simulation velocity contours and experimental schlieren diagram at H=8.74R

3.1.2 火箭垂直降落階段沖擊流場分析

由于在靜態過程中用于試驗的是直徑為16.52 mm的小噴管，這與實際工程中使用的火箭噴管有較大差距。因此在驗證完燃氣射流數值模型的準確性后，進一步考慮火箭的動態著陸過程，并使用更加貼合實際的噴管參數，在分析過程中采用如下假設：

1）火箭燃氣射流為可壓縮的理想氣體，不考慮燃燒、化學反應，忽略熱損失。不考慮多相流，火箭噴管入口的參數為恒定值。

2）假設垂直降落階段火箭以5 m/s 的恒定速度降落，并將火箭降落的速度等價于擋板靠近火箭尾噴管的速度。忽略由于噴出燃氣流所引起的箭體質量減少。

基于STAR-CCM+，該過程的模擬運動過程為2.6649 s，時間步長為60 μs，總迭代步數為44951 步，構建火箭垂直降落階段底部擋板所受沖擊流場的數值計算模型，得到擋板所受沖擊載荷的時歷曲線及擋板上距離射流軸線0 m 和4 m 處總壓的時歷曲線，如圖5所示。

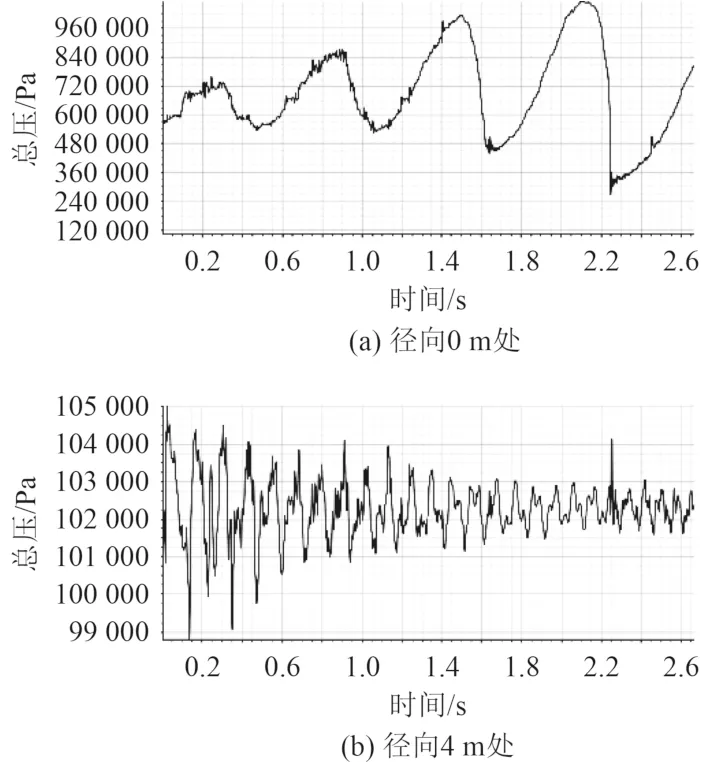
圖5 擋板上距射流軸線不同距離處的總壓隨時歷曲線Fig.5 Variation curve of total pressure with time at 0 m and 4 m from jet axis on baffle

從圖5 可以看出，隨著時間的增加，即火箭逐漸回落至甲板，徑向0 m 處的總壓值呈現震蕩增大的趨勢，總壓每隔大約0.6 s 出現一次極大值，分別在0.3 s時達到極大值730799 Pa，0.9 s 時達到870322 Pa，1.5 s時達到1012910 Pa，2.1 s 時達到1069260 Pa，總壓最大的震蕩幅值可達到794220 Pa。由于超音速射流特有的波系結構，如規律的菱形激波等，使得燃氣射流內的場變量并非均勻分布，因此在擋板逐漸靠近噴管的過程中，徑向0 m 處的總壓出現周期震蕩且逐漸增大的現象。當監測點位于徑向距離4 m 處時，監測點上的總壓呈震蕩收縮的趨勢，總壓最大的波動幅值為6100 Pa。隨后總壓震蕩幅值越來越小，圍繞102250 Pa進行小幅度震蕩，與標準大氣壓較接近，該點處不出現大幅波動增長現象的原因，可能是射流在擋板沿徑向傳播過程中能量耗散較大。

如圖6 所示，在火箭回落過程中，燃氣尾流對回收船舶甲板上的沖擊載荷呈小幅波動且逐漸震蕩收縮的趨勢，并最終維持在20400 kN 左右。由于船舶型寬40 m，同噴管出口直徑1524 mm 相比較大，射流主要是在擋板中心處形成較大的局部壓強，在徑向距離4 m處總壓隨時間的變化就已不明顯，而對比0 m 及4 m處的總壓時歷曲線可知，總壓值的波動隨著徑向距離的變大而變小，所以在擋板沿徑向超過4 m 處的部位，受到的總壓也應是震蕩收縮的，且比4 m 處的波動更小。而移動過程中射流的作用面積在穩定之后就無變化，射流對甲板的沖擊載荷計算可由總壓在作用面積上的積分得到。因此在積分之后，沖擊載荷的大小呈現震蕩收縮的趨勢。

圖6 火箭回收過程中甲板受到的沖擊載荷時歷曲線Fig.6 Time history curve of impact load on deck during rocket recovery

3.1.3 全過程沖擊載荷分析

上文模擬的沖擊載荷為垂直降落階段的結果，由SpaceX 的海上火箭回收流程表2 可知[8]，仍需補充從著陸點火開始至火箭平穩著陸完整過程的沖擊載荷時歷曲線，該過程持續約31 s。氣動控制階段火箭發動機關閉，從480 s開始進行著陸點火，甲板開始受到射流的沖擊載荷。根據關鍵時間點及該點的沖擊載荷大小，定全過程沖擊載荷的表達式，如下式：

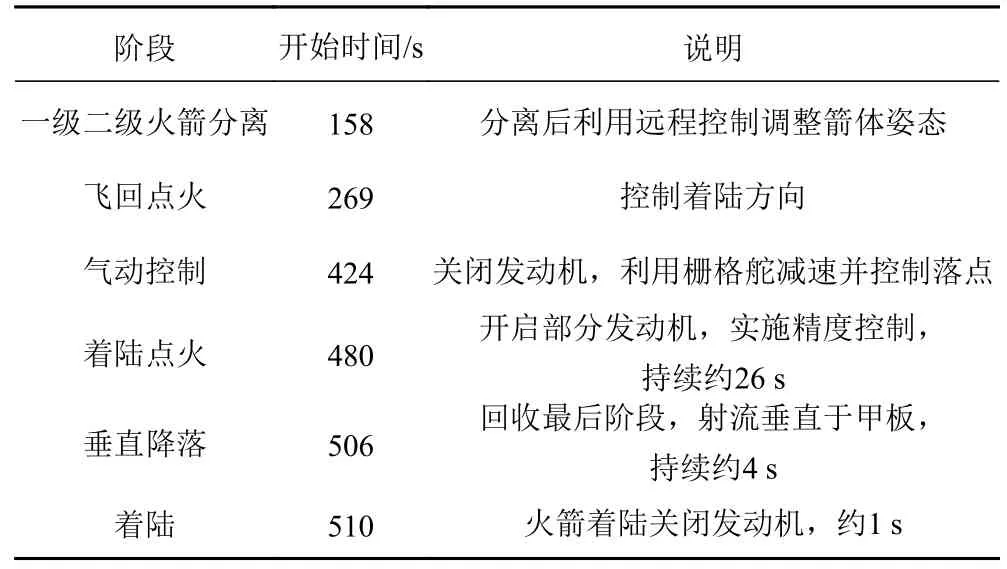
表2 “獵鷹九號”一級火箭回收主要時間節點[8]Tab.2 Main time node of Falcon 9 rocket recovery

其中，t1～t2為著陸點火階段，t1=480 s，t2=506 s。由于此時火箭離甲板較遠并且射流存在著不與甲板垂直的問題，因此假設該階段的沖擊載荷均勻增加；而t2至 t3為垂直降落階段，其中t3為510 s，基于圖6 可以得到5 0 6～5 0 8.6 6 4 9 s 的數值，并可以得到在508.6649～510 s 時間內的沖擊載荷約為20400 kN。t3～t4為火箭著陸關閉發動機甲板面沖擊載荷散去的過程，假設此階段的總時間為1 s，則t4為511 s。

3.2 不同火箭落點對船舶運動響應的影響

海上火箭回收過程中船舶處于運動狀態下，而火箭的落點位置對船舶的運動有很大的影響。Space X 公司海上火箭回收的落點范圍在船中附近，本文沖擊載荷模型的計算域底部是一個直徑為40 m 的圓，類比Space X 公司將該圓的圓心布置在船體重心所對應的甲板位置，如圖7(b)所示。通過以下步驟討論：1）首先考慮靜水條件，在所選范圍內沿船長及左舷方向分別布置7 個回收點(偏心0 m，5 m，10 m，15 m 處)，分析其對沖擊載荷-系泊力耦合作用下船舶水動力性能的影響；2）考慮有波浪作用時不同落點對船舶水動力性能的影響。

圖7 回收落點范圍及具體落點示意圖Fig.7 Specific falling point diagram of recovery

3.2.1 靜水中的船舶運動分析

圖8 為回收船舶在靜水中受沖擊載荷-系泊力耦合作用下不同回收落點的運動時歷曲線。可知，火箭沖擊載荷的作用時間為火箭發射升空后的480～511 s。對落點沿船長分布時的船舶運動對比分析如圖8(a)所示，結果表明，縱搖運動受動態沖擊載荷作用的效果最為明顯，且偏心距離越大，縱搖偏移量也越大，極大值約為0.25°，而橫搖運動的偏移量隨偏心距離的增大而減小，但其幅值較小基本為0，垂蕩運動基本不受落點的影響。如圖8(b)所示當回收落點沿船寬分布時，橫搖的變化最為明顯，且偏心距離越大，橫搖偏移量越大，極大值為2.858°。而縱搖運動幅值隨偏心距離的增加而減小。

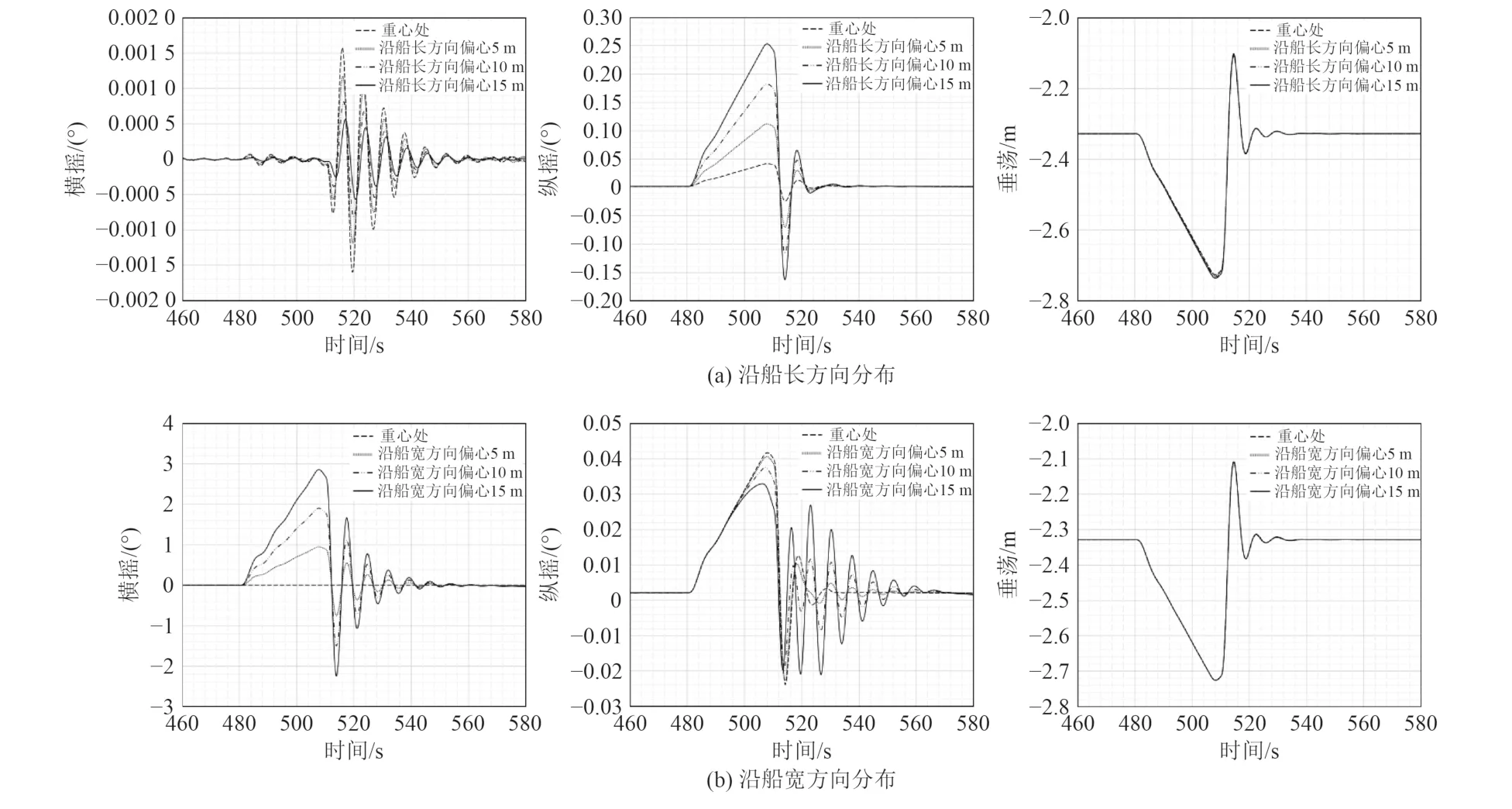
圖8 靜水狀態下不同落點的船舶運動時歷曲線Fig.8 Time history curve of ship motion with different rocket landing points distributed along the bow

3.2.2 波浪下船舶運動分析

針對回收船舶在燃氣射流沖擊載荷-波浪力-系泊力耦合作用下不同回收情況的橫搖、縱搖和垂蕩運動時歷結果展開研究，并以無沖擊載荷時的運動曲線作為對照。回收船舶的設計作業海況為4 級海況，隨機入射波浪應用JONSWAP 譜，譜峰因子為3，有義波高為1.75 m，譜峰周期為4.5 s，浪向為135°。

對于作用點沿船長方向分布的垂向載荷來說，從圖9 可以看出，隨著偏心距的增大，縱搖偏移量明顯增加，極大值為0.267°。該規律與靜水時相似，但波浪力的作用使縱搖幅值增加了0.017°，需注意的是無沖擊載荷作用時的縱搖偏移量要小于有沖擊載荷作用時的結果。而橫搖的運動幅值基本不受沖擊載荷的影響，可能是波浪力和系泊力的耦合作用抵消了沖擊載荷對橫搖的影響。火箭的回收落點位置對垂蕩運動影響并不明顯，但有無沖擊載荷對垂蕩運動影響顯著，前后狀態的差值約有0.41 m。

圖9 沿船長分布的不同落點船舶運動時歷曲線Fig.9 Time history curve of ship motion with different rocket landing points distributed along the bow side

從圖10 可知，當回收落點沿船寬方向分布時，不同的火箭落點對橫搖運動的影響最大。隨著偏心距的增大，橫搖的運動幅度增大，當回收落點沿左舷偏離重心15 m 時，其偏移量最大，此時船舶橫搖運動的極大值為2.898°，較靜水時的橫搖增加了0.04°。另外，無沖擊載荷作用與沖擊載荷作用在重心時的橫搖時歷曲線重合，這是因為沖擊載荷作用在重心時，沒有橫傾力矩產生，所以橫搖的幅值與無載荷作用時相差不大；在縱搖方面，基本滿足隨著偏心距離的增大，縱搖偏移量有所增加，但增幅不明顯；在垂蕩運動方面，偏心距的影響較小。

圖10 沿船寬分布的不同落點船舶運動時歷曲線Fig.10 Time history curve of ship motion with different rocket landing points distributed along the port side

4 結語

通過CFD 計算軟件STAR-CCM+及勢流水動力軟件Aqwa 模擬得到海上火箭回收過程中耦合作用下的船舶運動響應分析模型，分析有無波浪、沖擊載荷以及不同火箭落點對船舶橫搖、縱搖及垂蕩的影響，主要得到以下結論:

1）本文使用的數值模擬方法可用于海上火箭回收全過程中的船舶水動力計算，后續可以應用于不同的火箭、回收船舶或平臺上。

2）對于恒推力的火箭噴管，回落過程中燃氣尾流對甲板的沖擊載荷變化并不明顯，呈震蕩收縮的趨勢，最終維持在20 400 kN 左右；

3）最佳的火箭回收落點位置為船體重心所對應的甲板位置，此時船舶的橫搖縱搖及垂蕩運動偏移量最小，隨著偏心距離的增大，船舶運動幅值也會增大。當落點位于沿船寬偏心15 m 時，橫搖偏移量最大，約為2.898°。當回收落點位于沿船長偏心15 m 時，縱搖偏移量最大，約為0.267°。

4）根據回收船舶在作業海況及靜水狀態下的時歷曲線可知，中低海況波浪力的添加會增大橫搖和縱搖的極值偏移量，但其影響較不同火箭回收落點帶來的變化并不明顯。