基于MMC 的自修復材料結構與微膠囊的協同優化

李 鵬，張昌有，杜藝博，程文濤，占金青，唐 贛

（1.華東交通大學機電與車輛工程學院,江西 南昌 330013；2.華東交通大學載運工具與裝備教育部重點實驗室，江西 南昌，330013）

復合材料因其優異的力學性能，被廣泛應用于航空航天、汽車和電子等領域。然而，作為一種由多種異質/異形組元材料復合而成的新材料，其力學分散性較大，致使材料在生產和服役中易產生各類損傷，尤其是微裂紋的產生和擴展將引起材料力學性能的劣化，導致構件過早失效。損傷自修復[1]概念的提出為解決這一問題提供了有效途徑。

White 等[2]于2001 年首次提出微膠囊型自修復材料，并分析了微膠囊的分散性、幾何形狀與囊壁對修復性能的影響。Yu 等[3]研究了新鮮、短期老化和長期老化瀝青混凝土中微膠囊的形態結構、機械強度、熱穩定性以及愈合水平。Khan 等[4]研究表明，加入小直徑微膠囊的材料彈性模量有輕微減小，但斷裂韌性明顯增強，而隨著微膠囊直徑的增加，材料彈性模量和斷裂韌性均開始減小。Choi 等[5]將3D打印的微膠囊嵌入混凝土復合材料中，研究了微膠囊壁厚和打印方向對混凝土復合材料的影響。Wang等[6]采用分子動力學模擬了沿z 軸進行單軸拉伸的微膠囊自愈合混凝土的力學和界面性能。Han 等[7]提出了一種三維演化的微力學模型來定量解釋了微膠囊對裂紋損傷的自愈合作用。Nassho 等[8]將微膠囊嵌入到層板中，在短梁剪切試件上進行實驗并表明，隨著微膠囊濃度和粒徑的減小，層合板的剛度和表觀層間剪切強度增大但愈合效率也會隨著降低。Chowdhury 等[9]通過偶聯劑改性方法改善顆粒在復合材料中的分布。在化學方法中偶聯劑改性，會增加微膠囊與樹脂界面的黏合力，有利于材料力學性能的提高[10-11]。

在國內，王瑞等[12]通過偶聯劑對微膠囊表面進行改性，研究了微膠囊在材料中的分布以及改性后自修復材料的拉伸性能。郭瑞泉等[13]通過萬能試驗機研究了微膠囊直徑和用量對環氧樹脂力學性能的影響。肖春平等[14]研究了4 種不同粒徑（180，230，280，370 μm）的微膠囊及其體積分數對材料力學性能和自修復性能的影響。賀子騰[15]制備并研究了苯乙酸乙酯微膠囊直徑和體積分數對自修復涂層性能的影響。李鵬等[16]對自修復載體的無壁化設計和分布開展了一些相關研究，并通過實驗研究取得一定程度的成果。

近年來，國內外學者針對微膠囊的體積分數、幾何形狀及分布等內容進行了大量優化研究，然而優化設計的對象僅限于微膠囊載體，對結構宏觀構型與內置微膠囊進行協同優化的研究尚未見報道。研究基于可移動變形組件法，通過自修復材料的結構與微膠囊協同優化，在保證材料與微膠囊力學兼容性的基礎上，實現材料的損傷自修復設計。

1 內置微膠囊的二維組件

為實現結構宏觀構型和內置微膠囊載體的協同優化，研究基于可移動變形組件法，建立內置微膠囊組件的數學模型。以顯式的超橢圓方程描述組件[17]。其表達方式如下

式中：

圖1 是對組件中微膠囊中心點坐標的說明。

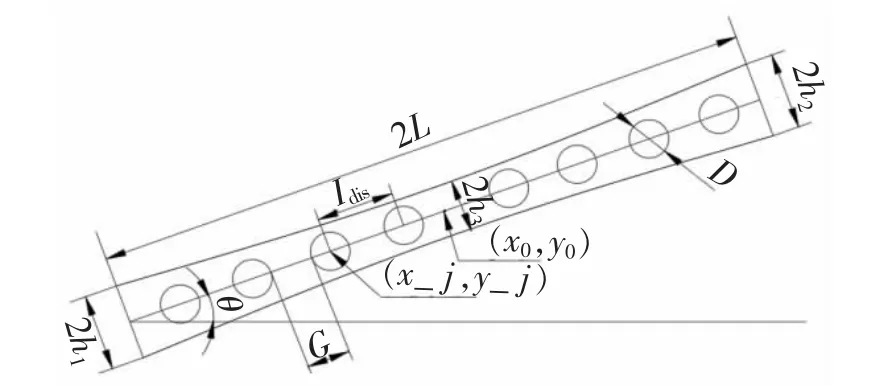
圖1 微膠囊中心點坐標說明Fig.1 The center point coordinates of the microcapsule

在式（1）～式（10）中，χi（x，y）表示內置微膠囊的二維組件；χ0（x，y）表示無膠囊的原始組件，χj（x，y）表示微膠囊；max 表示設計域中有限元節點取值為原始組件與微膠囊在該節點的最大拓撲描述函數值；L 為原始組件在x'方向上的半長；f（x'）表示原始組件在y'方向上的半寬；f（x'）可以根據實際優化的需要改變其參數（h1，h2，h3），表示為均勻寬度、線性變化寬度或二次變化寬度等不同的形式；p 為偶整數，一般取p=6；θ 表示原始組件在二維平面內逆時針方向的角度，內置微膠囊與所在的組件取相同的角度，其中st=sinθ，ct=cosθ；（x0，y0）表示原始組件中心點的坐標；r 表示微膠囊的半徑，由組件縮放而來；a 和G 表示為微膠囊的初始參數，其中G 表示兩個微膠囊之間的間距，a 表示半徑系數，這兩個參數決定了微膠囊的大小與分布；（x″，y″）因每個微膠囊的中心點坐標不同，而擁有不同的形式，（x-j，yj）表示第j 個微膠囊的中心坐標；floor 表示向下取整；Idis表示兩個相鄰微膠囊的中心點長度的距離。圖2 為內置微膠囊二維組件圖。

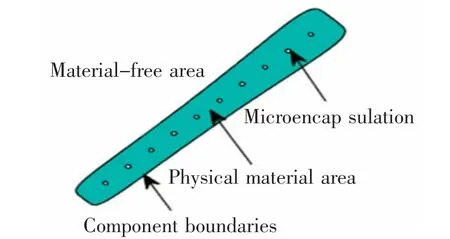
圖2 內置微膠囊組件Fig.2 The built-in microcapsules components

2 內置微膠囊拓撲優化問題列式

研究以結構柔度作為衡量材料與微膠囊力學兼容性的指標，考慮給定體積約束下以結構柔度最小為目標函數的拓撲優化，即求出在規定約束和荷載條件下使結構變形最小的最佳拓撲構型。優化列式如下

在式（11）中，C 為結構柔度；Xi=（，sinθi）,i=1，…，n，為第i 個內置微膠囊組件的設計變量；H 為Heasivide 函數；χ 為整體結構的拓撲描述函數；f 為內置微膠囊的二維組件所受的體積力；u 為結構位移場；t 為Neumann 邊界Γt上的面力；q 為懲罰因子，這里取q=2；E 為四階彈性張量，且其表達式為E=E/（1+v）［Ⅱ+v/（1－2v）δ?δ］，其中E 和v 分別為實體材料的彈性模量和泊松比，Ⅱ和δ 分別為四階單位張量和二階單位張量；ε 為二階線性應變張量；是實體材料的體積上界；v 為定義在實體材料所占區域上滿足Uad=｛v|v∈H1（Ω），v=0 on Γu｝ 的試探函數；UX表示設計變量所屬的可行域；為Dirichlet 邊界Γu上的給定位移，為了簡化分析，文中取=0。

3 數值分析

3.1 二維有限元分析

研究基于MMC 框架的拓撲優化方法，采用“代理材料模型”進行有限元分析，由式（1）計算出每個節點的拓撲描述函數值，則單元格的彈性模量按以下公式插值

式中：為了保證全局剛度矩陣的非奇異性，α 是一個很小的正數；ζ 表示一個正則化參數，其作用是用來控制正則化的寬度。

3.2 靈敏度分析

研究因為基于可移動變形框架的優化方法，因此采用伴隨法可直接推導目標函數C 對內置微膠囊組件各個設計變量的靈敏度，如下

以及約束條件V 內置微膠囊組件各個設計變量的靈敏度，如下

在式（14）～式（15）中，x 表示X=（（X1）T，…，（Xi）T，…，（Xn）T）T中的任意變量；K 表示結構的整體剛度，NE 表示單元格的數量；ke表示單元剛度矩陣。

3.3 優化算法

研究采用移動漸進算法（序列凸規劃法）作為優化求解器用于對拓撲優化問題的求解。移動漸近線算法最初由瑞典數學家Svanberg[18]最早提出，它是將目標函數和約束條件轉化為在當前設計點的一階移動近似子問題，通過梯度法求解子問題的解作為目標函數的近似解。

4 算法流程

自修復材料結構與微膠囊的協同優化流程如下：

1）設定材料的原始參數、設計域大小、微膠囊參數、載荷等；

2）根據設計域大小，設計合理的網格大小、組件初始化參數、MMA 優化參數；

3）根據微膠囊的相關參數計算組件中每個微膠囊的中心點坐標，在求解整體結構的拓撲描述函數值時，微膠囊與組件相交顯示微膠囊；

4）利用有限元求解結構目標函數和約束條件；

5）利用有限差分原理計算目標函數與約束條件的靈敏度；

6）將MMA 作為優化器更新設計變量；

7）判斷是否滿足迭代終止條件：每100 次迭代的目標函數最優值連續10 次未被更新，則終止迭代。

二維協同優化流程圖如圖3 所示。

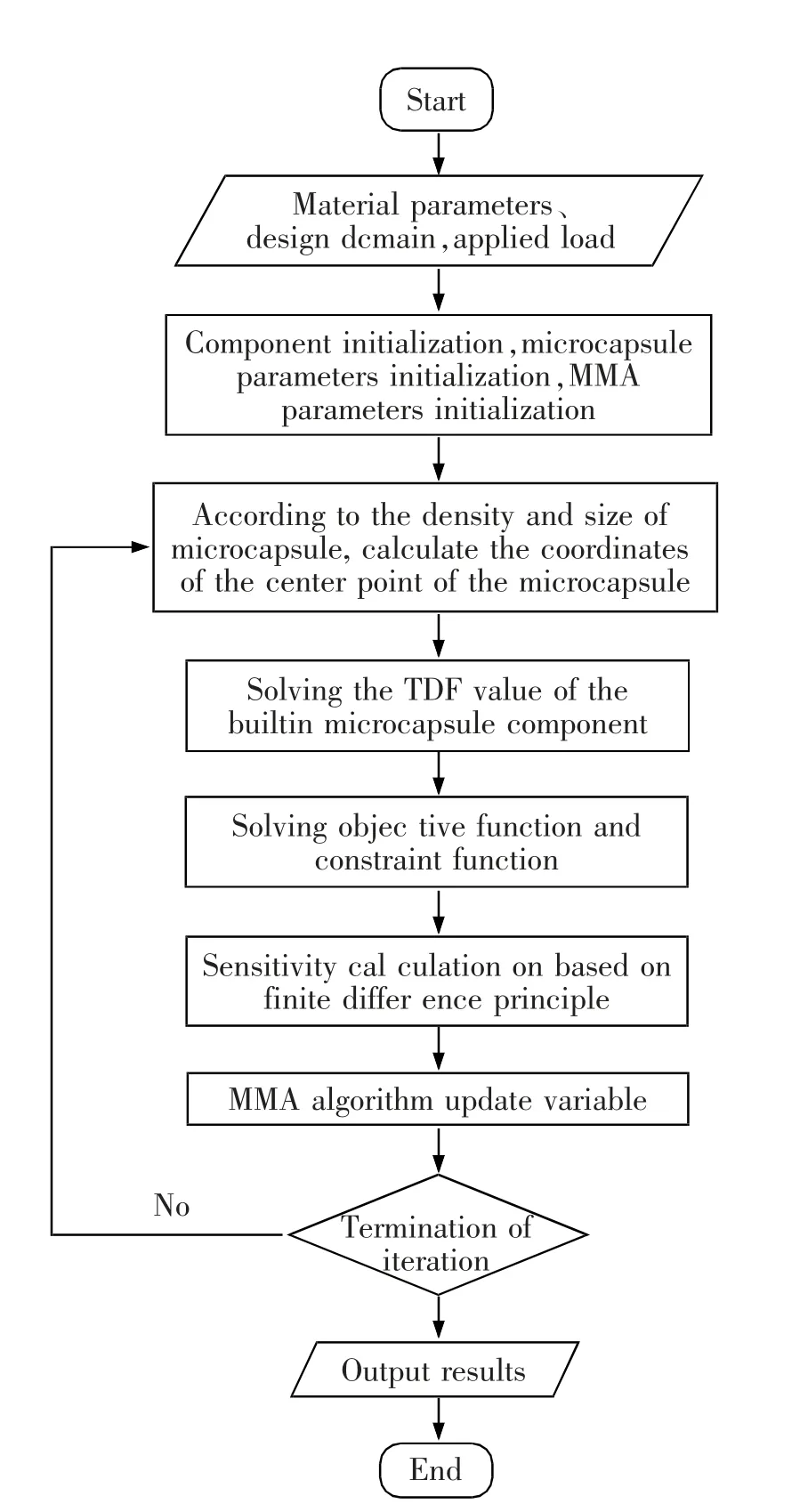
圖3 二維協同優化流程圖Fig.3 2D collaborative optimization flow chart

5 數值算例

為驗證自修復材料結構與微膠囊協同優化的有效性，研究采用二維MBB 梁算例，算例所涉及的彈性模量、材料密度、載荷以及幾何參數等信息均為無量綱，實體材料的彈性模量值設置為E=1，泊松比設置為v=0.3。

如圖4 所示，以MBB 梁的一側為設計域，長寬比為3∶1，設計域離散為450×150 的網格，右下角受滾動鉸鏈約束，左下角固定支撐，左上角受到豎直向下的載荷f=1。由于MBB 梁結構在此工況下具有對稱性，故優化時只取設計域的一側，對應的水平網格劃分和結構受力都減半，以結構柔度最小為目標，給定的面積約束上限為V≤0.3D，D 為設計域面積。

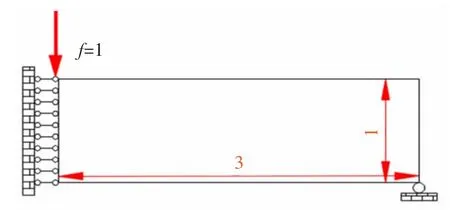
圖4 MBB 梁一側設計域Fig.4 One side of the design domain of MBB beam

圖5 為MBB 梁算例的初始設計，算例中共設計24 個組件。表1 給出了組件與微膠囊的初始設計參數。其中，第一和第二個組件的中心點坐標均為（0.25，0.25），傾角的正弦值分別為0.7 和-0.7。其他組件依次沿著x（或y）方向平移0.5 獲得，各組件中有6 個微膠囊，微膠囊的半徑系數a 為0.1，微膠囊之間的間距G 為0.1。

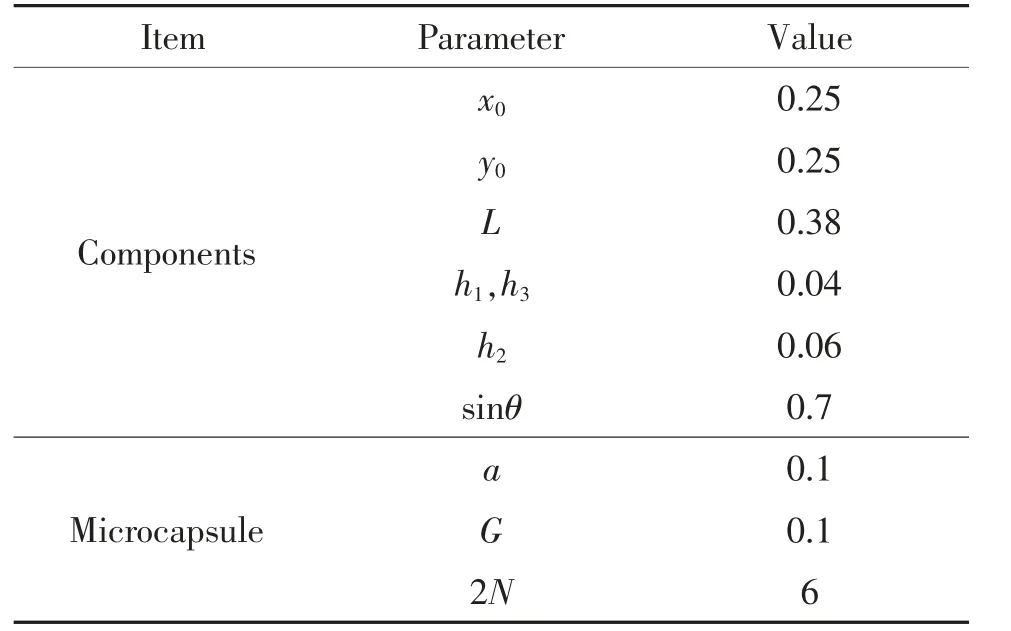
表1 MBB 梁內置微膠囊的組件初始設計Tab.1 Initial design of components with microcapsules in MBB beam

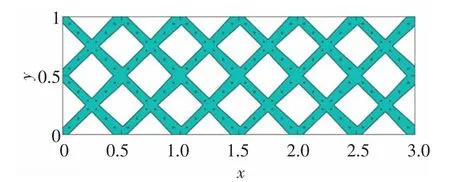
圖5 MBB 梁算例初始設計（a=0.1，G＝0.1）Fig.5 The initial design of MBB beam example（a=0.1，G＝0.1）

圖6 為基于MMC 方法的自修復材料結構與微膠囊協同優化的結果，即“協同優化自修復材料”。

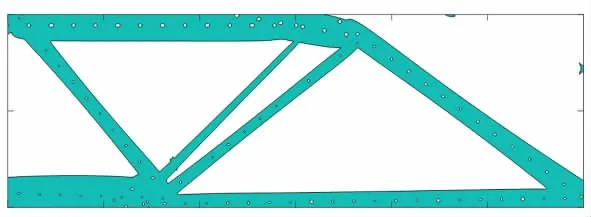
圖6 協同優化自修復材料拓撲優化構型（a=0.1，G=0.1）Fig.6 Optimize topology and configuration of collaborative self-healing materials（a=0.1，G=0.1）

為論證協同優化的效果，研究沿用經典自修復材料的設計方法。首先，基于MMC 方法獲取相同初始條件（如工況、邊界條件等）下無膠囊載體的拓撲優化構型（如圖7 所示，其柔度值為294.6）；其次，根據不同的微膠囊參數，在組件內嵌入微膠囊，設計“經典自修復材料”，并計算相應柔度和微膠囊體積分數（如表2 和圖8 所示），微膠囊體積分數是指拓撲優化構型中全部微膠囊所占的面積比，體積分數的取值范圍為[0，1）。研究結果表明。

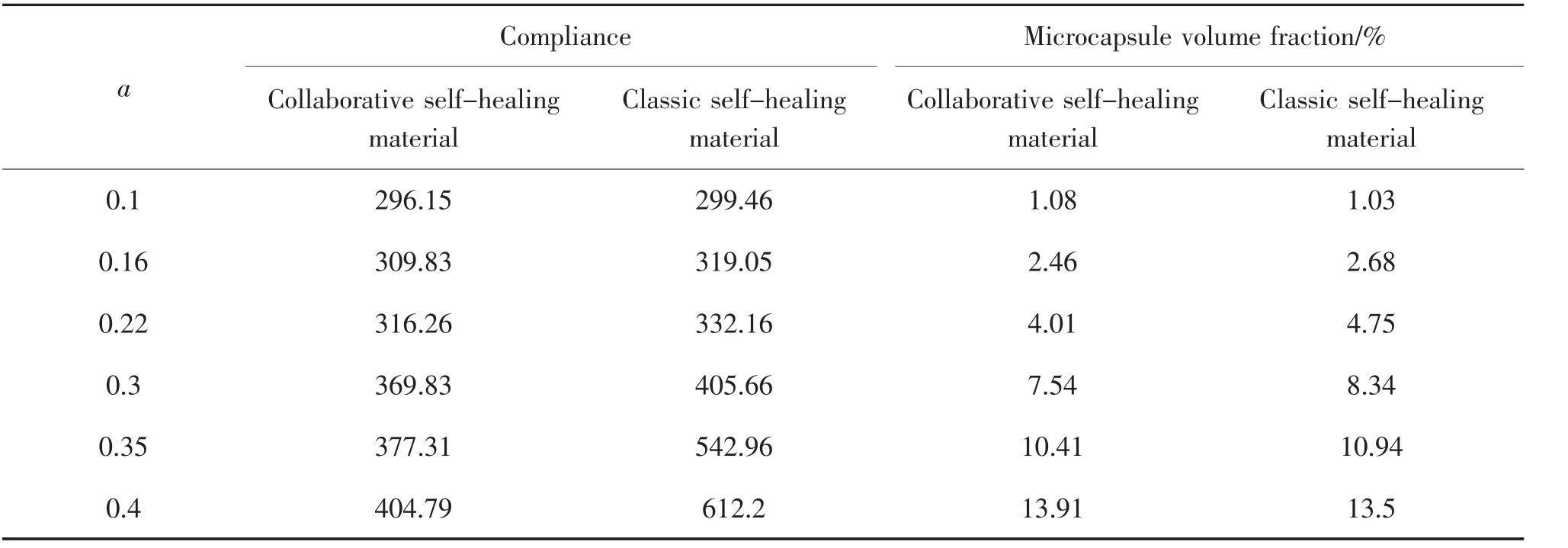
表2 不同微膠囊半徑系數a 下兩類自修復材料的優化結果Tab.2 Optimization results of two kinds of self-healing materials with different radius coefficients a of microcapsules

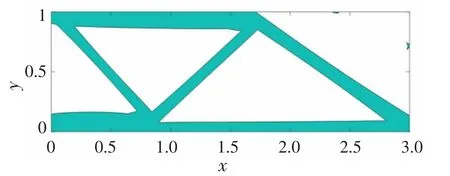
圖7 無膠囊載體拓撲優化構型Fig.7 Carrier topology optimization configuration without capsule

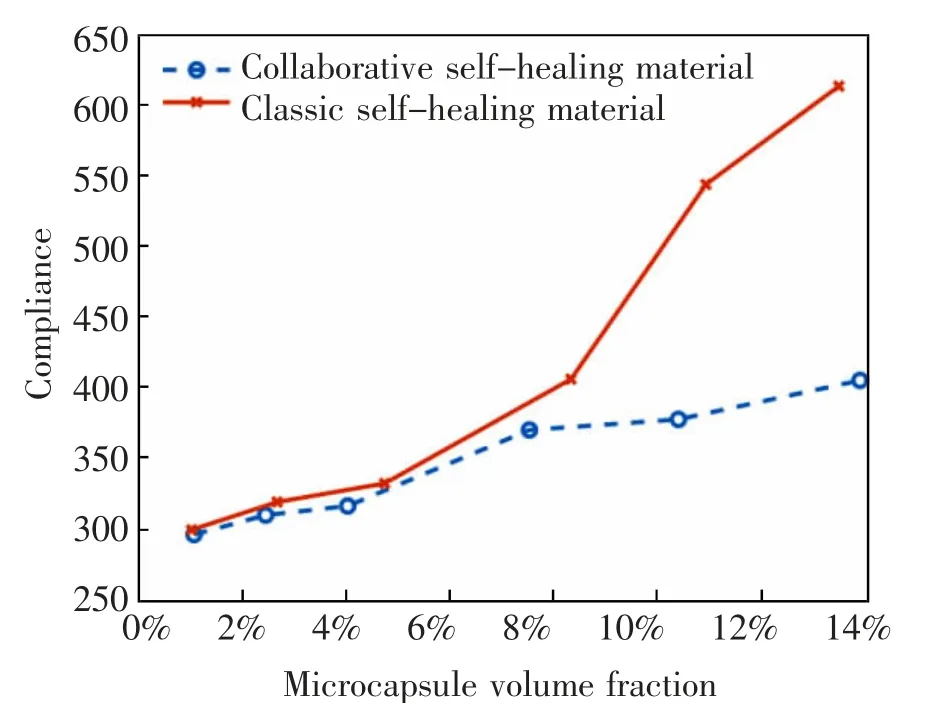
圖8 兩類自修復材料微膠囊體積分數與柔度關系Fig.8 Relationship between microcapsule volume fraction and compliance of two kinds of self-healing materials

1）對比無膠囊載體的MBB 梁優化構型（圖8），協同優化自修復材料（a=0.1，G=0.1）的柔度提高了0.53%，為296.15（表2），且構型具有相似性（圖6）。

2）由表2 可知，微膠囊參數決定了自修復材料載體的體積分數，當微膠囊半徑系數a 由0.1 增至0.4 時，兩類自修復材料的微膠囊體積分數均出現了增加趨勢；

3）由表2 可知，隨著微膠囊體積分數的提高，兩類自修復材料的柔度均出現了增加，然而增加的幅度存在明顯差異，圖8 為兩類自修復材料微膠囊體積分數與柔度關系曲線，顯然協同優化自修復材料的柔度均小于經典自修復材料，而且隨著體積分數的增加（尤其體積分數大于8%時），兩者的差別明顯變大。這說明對于經典自修復材料而言，當微膠囊體積分數大于8%時，微膠囊載體將造成結構力學性能的急劇劣化，而協同優化自修復材料則可減小這一不利影響。

4）通過研究不同微膠囊參數下兩類自修復材料的構型，進一步分析協同優化的效果。表3 給出了微膠囊半徑系數a 分別為0.16 和0.35 的兩類自修復材料構型，顯然相對于經典自修復材料而言，協同優化自修復材料通過宏觀構型的優化有效的減弱了載體對自修復材料力學性能的影響。

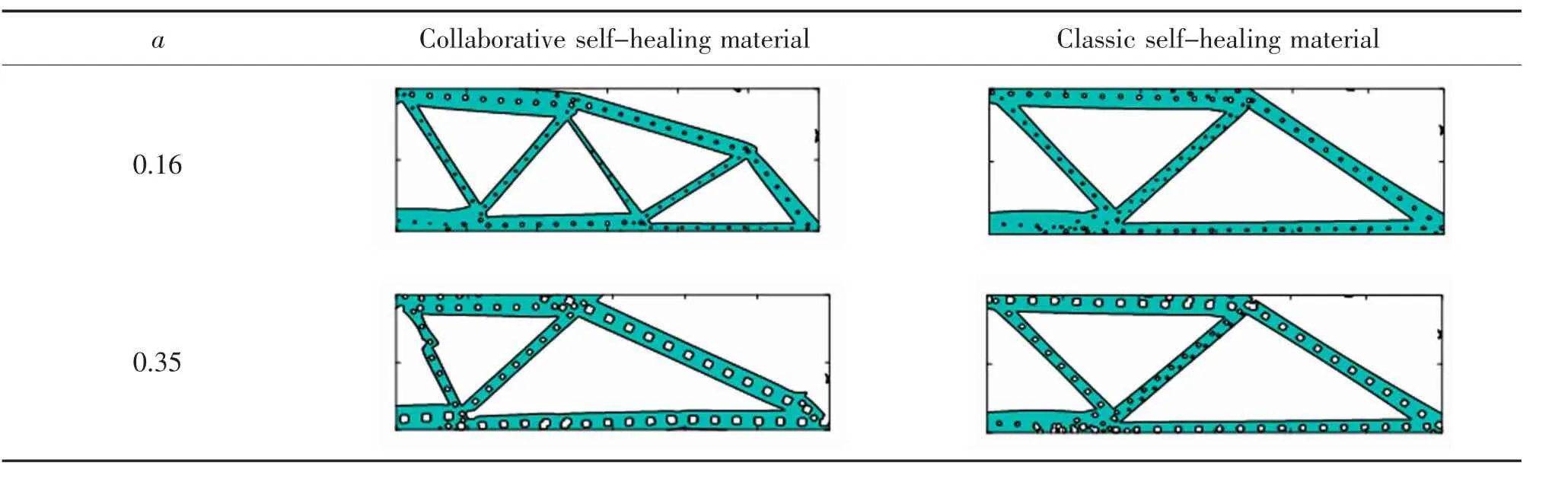
表3 兩類自修復材料拓撲優化構型Tab.3 Topological optimization configuration of two self-healing materials

6 結論

1）將無膠囊的MBB 梁拓撲優化構型與內置微膠囊的MBB 梁拓撲優化構型進行了對比，論證了內置微膠囊的MBB 梁在微膠囊體積分數較低的情況時，可以獲得與無膠囊的MBB 梁相似的拓撲優化構型，證明了引入協同優化方法的有效性。

2）隨著微膠囊體積分數的增加，將會造成兩類自修復材料的柔度增大，力學性能的劣化。

3）當微膠囊體積分數超過8%時，對于經典自修復材料，微膠囊會造成其結構力學性能的急劇劣化，當微膠囊體積分數接近14%時，協同優化自修復材料的柔度值僅為經典自修復材料的66.1%。可見研究提出的協同優化自修復材料，通過引入宏觀構型與微膠囊的并行優化機制，可有效的減小微膠囊體積分數增加對其結構力學性能的不利影響。