次分數(shù)跳-擴散模型下的復合期權(quán)定價
王竟莘,郭志東
(安慶師范大學 數(shù)理學院,安徽 安慶 246133)
期權(quán)在金融市場中扮演著重要的角色,擁有獨特的非線性損益結(jié)構(gòu),相較于其他工具,能夠構(gòu)造出不同的風險和回報組合,從而更好地達到避險保值的目的。期權(quán)定價的經(jīng)典模型是Black-Scholes模型,自1974年被Black和Scholes[1]提出后,學者們由此取得了豐富的研究成果。2004年,Bojdecki[2]等提出次分數(shù)布朗運動,除卻分數(shù)布朗運動擁有的特點以外,次分數(shù)布朗運動具有協(xié)方差隨時間增加而迅速衰減、增量在非重疊區(qū)間內(nèi)相關(guān)性較弱的特點,因此更適用于期權(quán)定價研究。Bian[3]在次分數(shù)基礎上引入模糊集理論并建立基于長期記憶特性的歐式期權(quán)定價模型,分析了不同Hurst 參數(shù)期權(quán)定價的不同。Kuang[4]研究了次分數(shù)下重正化加權(quán)立方變化的收斂性,數(shù)值模擬得到不同Hurst 參數(shù)下的樣本路徑。Li[5]等研究了次分數(shù)驅(qū)動下Vasicek模型的參數(shù)估計問題,對μ,θ兩個未知參數(shù)進行相合性和漸近分布估計,發(fā)現(xiàn)其具有一定的適用性。Araneda[6]等研究了混合次分數(shù)機制下具有CEV模型的歐式看漲價格,發(fā)現(xiàn)所提出的模型能夠捕捉不同期限期權(quán)價格的時間結(jié)構(gòu)。
復合期權(quán)是一種變異期權(quán),能夠有效規(guī)避外匯風險。Geske[7]首次提出復合期權(quán)定價理論,該期權(quán)創(chuàng)新性地將杠桿效應運用進期權(quán)定價,考慮股票收益率方差為股票價格水平的函數(shù),使復合期權(quán)能夠有效地估計公司負債、定價公司資本結(jié)構(gòu)。Hodges[8]發(fā)現(xiàn)復合期權(quán)估值公式是一系列多項式分布函數(shù)總和,給出了任一維數(shù)的多正態(tài)分布和的恒等式,簡化了恒等式積分數(shù)量并使復合期權(quán)估值效率得到提高。Li[9]等引入擴展方差伽馬過程來控制對數(shù)資產(chǎn)價格的偏度和峰度,得到解析式并進行數(shù)值計算。Liu[10]等引入跳-擴散過程,得到定價公式,且數(shù)值結(jié)果發(fā)現(xiàn)若跳躍振幅對數(shù)為雙指數(shù)分布能更好地捕捉非對稱leptokurtic特征和波動率微笑的現(xiàn)象。Wang[11]基于模糊集理論,對復合期權(quán)模型下利率和波動率兩個未知參數(shù)進行模糊,得到復合期權(quán)的模糊價格和模糊概率均值。劉明月[12]等建立多階段因果復合期權(quán),利用動態(tài)無套利均衡分析法得到了該模型下n階段看漲因果復合期權(quán)的定價公式。宮文秀[13]將三叉樹模型引入復合期權(quán)定價問題,利用向后倒退法對該模型進行定價,且由數(shù)值分析發(fā)現(xiàn)不同變量的變化與復合期權(quán)價格呈不同的正負相關(guān)性。王向榮[14]考慮同時將Hull-White利率模型和Ornstein-Uhlenbeck過程引入復合期權(quán),得到了該模型下復合期權(quán)的定價公式。溫小梅[15]研究復合冪期權(quán)定價問題,考慮雙隨機波動率跳-擴散模型并得到了其解析表達式,且數(shù)值分析發(fā)現(xiàn)變量對期權(quán)價格有較大影響。然而,上述研究并未探討次分數(shù)跳-擴散機制下的復合期權(quán)定價問題,基于此,本文將對該問題進行相關(guān)研究。
1 預備知識
1.1 次分數(shù)布朗運動
1.2 次分數(shù)跳-擴散模型
在該模型下,標的資產(chǎn)價格St滿足隨機微分方程
根據(jù)風險中性定價理論,可用無風險利率r(t)替換μ(t),根據(jù)It?公式,可求得方程(1)的解為
2 次分數(shù)跳-擴散模型下的Black-Scholes公式
定理1設標的資產(chǎn)價格St符合公式(2)給出的模型,則歐式看漲期權(quán)價格C(St,t)滿足偏微分方程
證明考慮一個投資組合Π包含一份期權(quán)C(St,t)和Δ份股票,其在t時刻這個投資組合的價格為∏=C-ΔS。假設Δ在時間區(qū)間(t,t+Δt)內(nèi)沒有變化,則選擇合適的Δ,使Π在時間區(qū)間(t,t+dt)內(nèi)無風險。
聯(lián)立公式(4)和公式(5),則定理1得證。
引理1若該期權(quán)到期時間為T,敲定價格為K,且遵循公式(2)和公式(3)給出的模型,則其價格可表示為
且跳-擴散歐式看漲期權(quán)的價格為[16]
即認為該期權(quán)價格為時段內(nèi)B-S 模型價格的加權(quán)平均,權(quán)重服從特征參數(shù)為λ′(T-T0)的泊松分布。公式(8)的為St服從幾何布朗運動的Black-Scholes公式,現(xiàn)假設其服從次分數(shù)布朗運動,對公式(8)進行相應代換并聯(lián)立公式(7),引理1得證,且有
3 次分數(shù)跳-擴散模型下復合期權(quán)定價公式
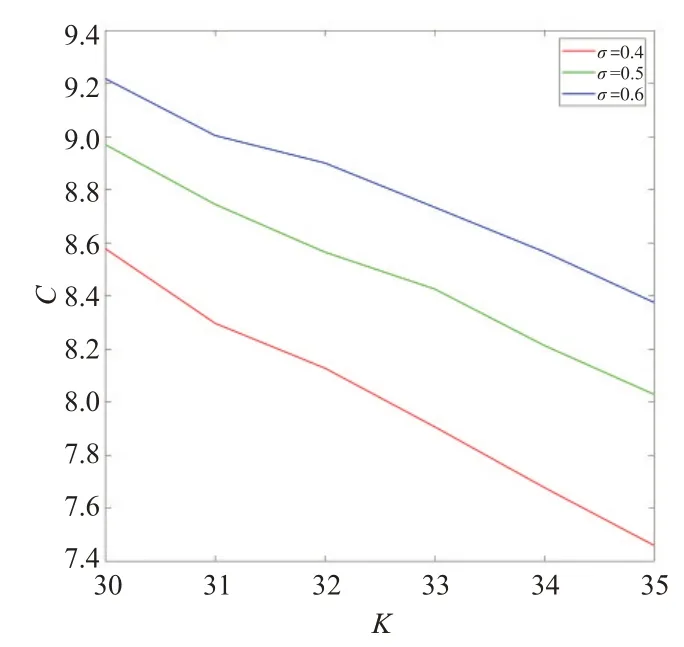
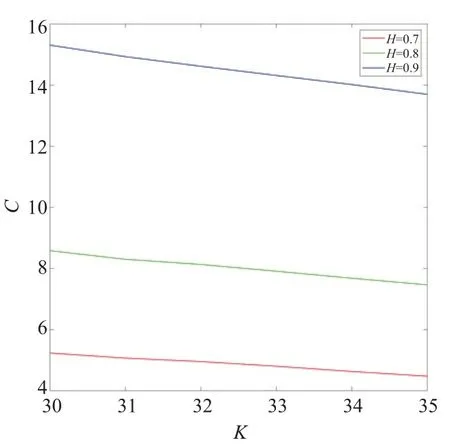
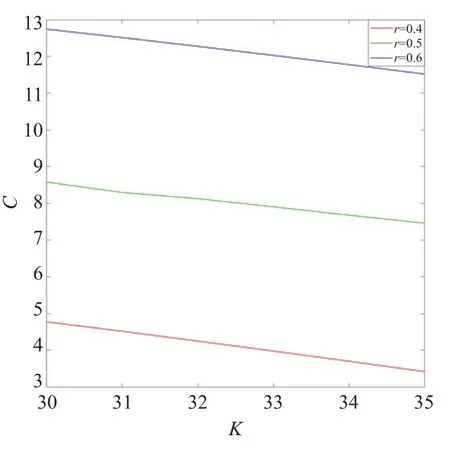
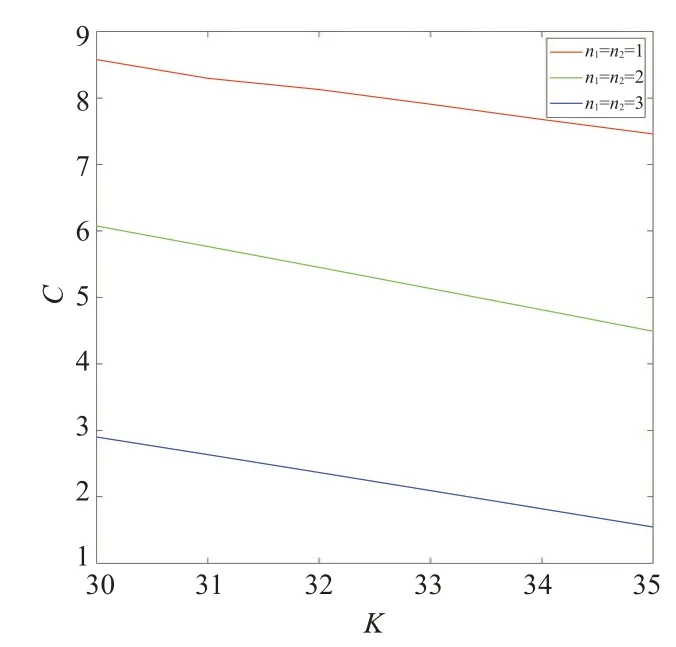
定理2考慮一個看漲期權(quán),到期日為T2,中途有到期時刻T1,其行權(quán)價格為K1,當T1 其中Φ2(a,b,ρ)為二維累計概率分布函數(shù),且有 證明設CC[C(K,T2),K1,T1]為該復合期權(quán),當C(S1,K,T1,T2)>K1時,認為應在T1時刻執(zhí)行該復合期權(quán)。當C(S1,K,T1,T2) 或當ST>K時,該復合期權(quán)可在T2時刻執(zhí)行。由風險中性定價理論,此時復合期權(quán)價格可表示為 由此將目標求解問題等價轉(zhuǎn)化為對兩個期望的求解。并基于泊松過程,根據(jù)[T0,T1]和[T1,T2]區(qū)間上的跳躍數(shù)對期望進行調(diào)節(jié),分別用n1和n2表示兩時段內(nèi)的跳躍次數(shù),且m=n1+n2為[T0,T2]區(qū)間內(nèi)跳躍的總數(shù)。 可將公式(11)第一個期望表示為 則公式(12)第二項的解為 同理,可得公式(12)第一項的解為 綜合公式(14)和公式(15),可得公式(11)第一個期望的值為 同理,可得公式(11)第二個期望的值為 此處a2定義同上公式(17),聯(lián)立公式(13)、公式(16)和公式(18),則定理2得證。 用Matlab編程計算給出了一些本文模型的數(shù)值模擬結(jié)果,并與常用模型進行了比較,模擬采用的參數(shù)(當對某一變量進行分析時,其余變量取值不變):r=0.5,σ=0.4,σJ=0.05,H=0.8,n1=1,n2=1,k=0.4,T0=0,T1=1,T2=2,K1=10,S0=40,K=[30,31,32,33,34,35]。若以σ為變量,令其分別為0.4、0.5、0.6,數(shù)值模擬結(jié)果如圖1;若以H為變量,令其分別為0.7、0.8、0.9,數(shù)值模擬結(jié)果如圖2;若以r為變量,令其分別為0.4、0.5、0.6,數(shù)值模擬結(jié)果如圖3;若以n1、n2為變量,令其分別同時跳躍1、2、3次,數(shù)值模擬結(jié)果如圖4。 圖1 σ為變量時數(shù)值模擬結(jié)果 圖2 H為變量時數(shù)值模擬結(jié)果 圖3 r為變量時數(shù)值模擬結(jié)果 圖4 n1、n2為變量時數(shù)值模擬結(jié)果 由圖1-4可得結(jié)論一:次分數(shù)跳-擴散機制下復合期權(quán)的價格隨著σ,H,r的增大而增大,隨著n1、n2的增大而減小。從增減幅度來說,隨著相應變量的增大,圖2復合期權(quán)價格的增幅最大,說明復合期權(quán)價格對H的變化比對其他三個變量更加敏感;另一方面,同等條件下,隨著K的增大,復合期權(quán)價格逐漸減小。 若以T1為變量,令其分別為0.5和1,本模型數(shù)值模擬結(jié)果如表1所示,可得結(jié)論二:同一T1下,該復合期權(quán)的價格隨K的增加而逐漸減小。同K下,該復合期權(quán)的價格隨T1的增大而減小明顯。 表1 復合期權(quán)的數(shù)值模擬結(jié)果 綜上,基于模型對六個變量的數(shù)值模擬結(jié)果可發(fā)現(xiàn),σ、H、r增大復合期權(quán)價格增大,n1、n2、T1、K增大復合期權(quán)價格減小。 此外,本文分別對標的資產(chǎn)服從幾何布朗運動、分數(shù)布朗運動和分數(shù)跳-擴散的復合期權(quán)進行相應數(shù)值模擬,結(jié)果與本模型的對比分別如圖5、圖6 所示。可知,三個模型的數(shù)值結(jié)果也都符合結(jié)論二的相關(guān)規(guī)律。此外,由圖1-2可看出,相同條件下幾何布朗運動模型的數(shù)值結(jié)果始終最小;分數(shù)跳-擴散模型的數(shù)值與本文模型較為接近;分數(shù)布朗運動模型模擬數(shù)值始終最大。 圖5 T1=0.5時四種模型對比結(jié)果 圖6 T1=1時四種模型對比結(jié)果 數(shù)值模擬結(jié)果的總體趨勢與文獻[13]的結(jié)果相一致,符合復合期權(quán)價格的基本特征。由于跳躍的存在,會使得期權(quán)的實際價格相比于經(jīng)典B-S 模型偏高[15,17],本文的數(shù)值結(jié)果也與此相符。此外,由于次分數(shù)布朗運動具有協(xié)方差隨時間的增加而迅速衰減、增量在非重疊區(qū)間內(nèi)相關(guān)性較弱的特點,從數(shù)值結(jié)果可以看出相比分數(shù)布朗運動,復合期權(quán)的價格會偏低,這也與實際相符。因此可認為本文模擬結(jié)果較為可靠,次分數(shù)跳-擴散模型應能更準確地刻畫標的資產(chǎn)特征,并具有一定的實踐性。 本文探究了次分數(shù)跳-擴散模型下復合期權(quán)的定價問題。基于風險中性測度假設,運用伊藤公式和Δ對沖方法,得到了看漲的歐式看漲期權(quán)滿足的偏微分方程。運用泊松過程給出了該模型下復合期權(quán)價格的顯式表達公式。通過數(shù)值計算,探究了多個變量對復合期權(quán)價格的影響,并將本文模型與三個常用模型進行對比,發(fā)現(xiàn)數(shù)值規(guī)律具有一些共性。4 數(shù)值模擬
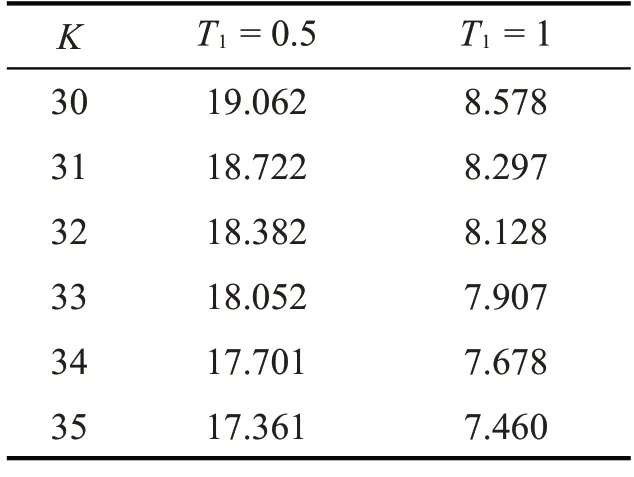
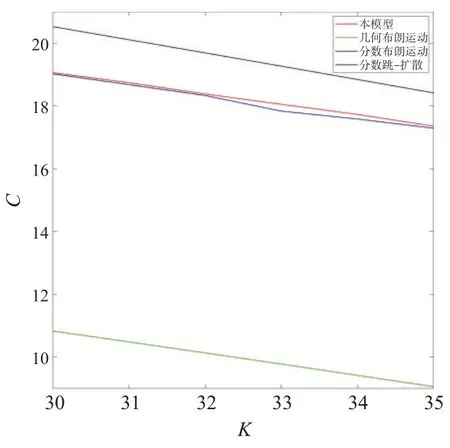
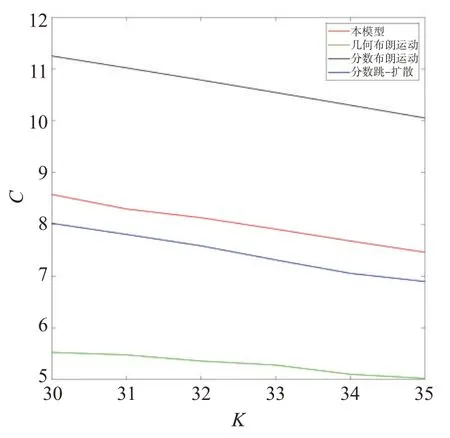
5 結(jié)束語

