縱垂式波浪能裝置的最大輸出功率設計

羅焙琢 羅洋洋 楊亞洲

摘? 要：波浪能分布廣泛，儲量豐富，具有可觀的應用前景。文章對波浪能轉換能量裝置的基礎結構進行研究，并就其作用機理分析了裝置在波浪能下的最大輸出功率現狀。同時，對海平面產生波浪時，裝置在受力情況下的垂蕩運動模型與縱搖運動模型進行研究，利用牛頓第二微分定律與微分轉動慣量定律尋找兩種運動模型的關聯性與限制條件；在此基礎上，對功率進行積分得出裝置在兩種不同運動狀態下的輸出功率，最后再將兩個功率相加構建出最終功率輸出模型，并找到裝置產生最大功率時對應的各部件參數結果。

關鍵詞：受力分析；牛頓第二微分定律；微分轉動慣量定律；功率積分

中圖分類號：TM619；TP39? 文獻標識碼：A? 文章編號：2096-4706（2023）05-0054-06

Design of Maximum Output Power of Vertical Wave Energy Device

LUO Beizhuo， LUO Yangyang， YANG Yazhou

（Sichuan University Jinjiang College， Meishan? 620860， China）

Abstract： Wave energy， with its wide distribution and abundant reserves， has considerable application prospects. This paper studies the basic structure of the wave energy conversion device， and analyzes the current situation of the maximum output power of the device under the wave energy according to its mechanism. At the same time， the heave motion model and pitch motion model of the device under the force condition when waves are generated at the sea level are studied， and the correlation and restriction conditions of the two motion models are found by using Newton's second law of motion and Law of differential moment of inertia; On this basis， the output power of the device under two different motion states is obtained by integrating the power. Finally， the final power output model is built by adding the two powers， and the corresponding component parameter results when the device generates the maximum power are found.

Keywords： force analysis; Newton's second law of motion; Law of differential moment of inertia; power integration

0? 引? 言

隨著經濟和社會的發展，人類面臨能源需求和環境污染的雙重挑戰，發展可再生能源產業已成為世界各國的共識。占地球總面積71%的海洋首先進入開發者的視線，目前被主要關注的海洋能包括潮汐能潮流能、波浪能、溫差能和鹽差能等，而波浪能分布廣泛，儲量豐富，具有可觀的應用前景。波浪能裝置的能量轉換效率是波浪能規模化利用的關鍵問題之一。

波浪能是指海洋表面波浪所具有的動能和勢能，按波浪能的利用方式，波浪能發電可大致分為利用波浪能的垂直運動、利用波浪能的水平運動、利用波浪的水壓、利用波浪水質點的運動等形式。按基本原理又可分為利用物體在波浪作用下產生的振蕩和搖擺運動、利用波浪壓力的變化、波浪沿岸爬升時產生的水勢能三種方式，而這三種方式也就是我們通常所指的氣動式、液動式和蓄水式。本文將利用波浪能對裝置產生的垂蕩和縱搖運動方式時的功率輸出進行分析。

1? 垂蕩運動模型的構建

1.1? 平衡模型

本文研究的裝置如圖1所示。

因為浮子與振子的重量占總裝置質量過大，所以可以忽略中軸，底座及PTO的質量，以此方便我們進行研究，此外由于研究的裝置內各個系統之間采用了摩擦系數很低的配件，所以整個系統產生的較小摩擦力也能忽略不計。仿真模型各零件參數設置如表1所示。

然后我們根據實際研究得出相關的運動參數如表2所示。

我們設置初始狀態下，整個裝置在重力和浮力兩個力的作用下處于平衡狀態，可求出裝置露出水面的高度：

V=1/3πR2（h-h1）+πR2（H-H1）? ? ? ? ? ? ? ? ? ?（1）

R為圓柱半徑，h為圓錐高度，h1為圓錐高出水面的高度，H1為圓柱露出水面的高度，可以算出平衡狀態下浮子露在空氣上的高度H1。

1.2? 垂蕩運動受力分析

1.2.1? 浮子運動

因為初始狀態下浮子受外力作用，使之做垂蕩運動（由于浮子一開始就從平衡狀態下開始運動，因此在分析合力時可以不再考慮浮子的重力和浮力）我們在浮子初始位置處建立三維直角坐標系，規定沿Z軸方向為正方向，如圖2所示。

根據研究，浮子在運動過程中受力有如下情況：

（1）波浪激勵力fd=fcosωt。浮子在受該力的作用下其方向將根據時間的變化而變化。

（2）靜水恢復力F。因為浮子自身運動使其浸水部分的體積發生變化而產生的。根據其實際運動情況，可以求出浮子在運動產生的位置變化時受到的靜水恢復力。該力方向始終為浮子的初始狀態時刻重力與浮力的平衡點處，此時先分析F為正的情況：

下沉時浮子的柱體在水中的體積增大，此時靜水恢復力大小為浮子的浸水體積增加部分的同體積水的重量ρgv排水，方向向上為正方向。

F=ρgπR（H-H1）? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（2）

上浮時需要分解成為兩種情況：第一種情況是浮子浸水體積減小，最大上浮高度可以使水面剛好沒過柱體的下底部分，此時柱體將完全露出水面，靜水恢復力大小（方向向下）：

當上浮時浮子浸水體積減小并達到浮子柱體靜止最大過程。

浮子柱體完全出水后，即為錐體露出水面的過程。由此推出：

F=ρgπR2（H-H1）-ρg{1/3πR2h-[1/3πR2（h-h1）+πR2（H-H1）]}（3）

（3）興波阻尼力fw。即浮子做垂蕩運動時，波浪產生造成對浮子運動的阻力。興波阻尼力與垂蕩運動的速度成正比，并且方向相反。分析可知：

（4）

其中B為阻尼系數， 為浮子相對速度。

（4）振子反作用力fa。但是要從內部振子分析fv，先得到振子的運動方程。

1.2.2? 振子運動

為了受力分析以及計算數據量的方便，設振子的相對運動位移量為。以振子底座為XOY的平面，中軸Z軸構建三維坐標面，如圖3所示。

振子將受到彈力和直線阻尼器（發電裝置）的合力作用，并結合微分牛頓第二定律，振子的反作用力：

（5）

其中? 為振子加速度，K為直線阻尼器系數，R為彈簧剛度。

根據式（5），振子運動時受力情況如圖4所示。

因為fa=-fv，我們得到了浮子在垂蕩方向的運動模型：

1.3? 垂蕩運動模型

綜上，裝置在垂蕩運動的完整運動方程：

（6）

為了求解微分方程，根據探究，我們將阻尼系數分為兩種情況。

情況1的K阻尼系數是一個常數為10 000，代入式（6）得到的結果如圖5、圖6所示。

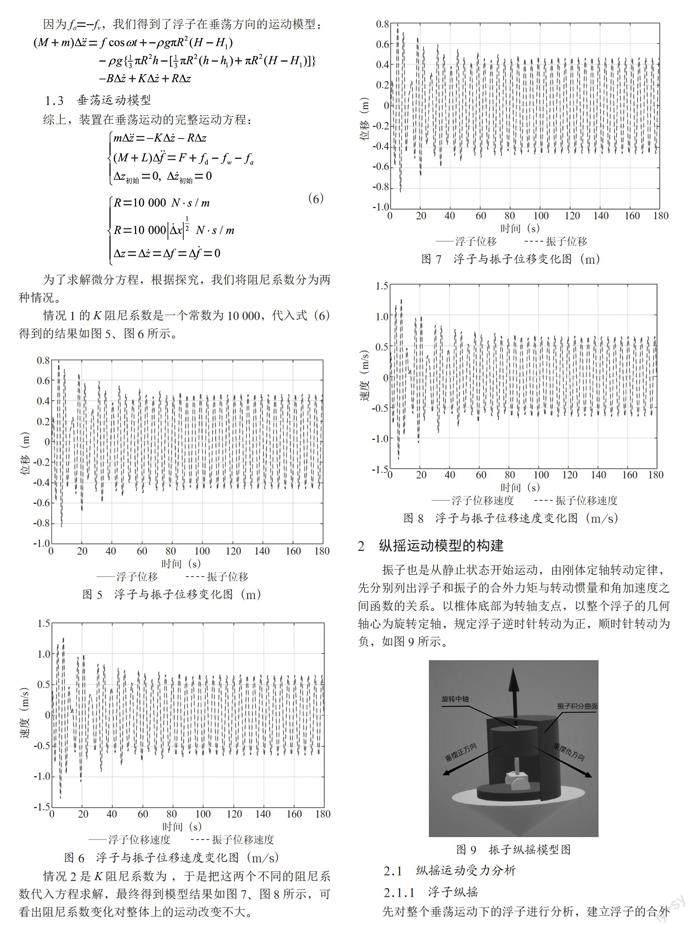
情況2是K阻尼系數為 ，于是把這兩個不同的阻尼系數代入方程求解，最終得到模型結果如圖7、圖8所示，可看出阻尼系數變化對整體上的運動改變不大。

2? 縱搖運動模型的構建

振子也是從靜止狀態開始運動，由剛體定軸轉動定律，先分別列出浮子和振子的合外力矩與轉動慣量和角加速度之間函數的關系。以椎體底部為轉軸支點，以整個浮子的幾何軸心為旋轉定軸，規定浮子逆時針轉動為正，順時針轉動為負，如圖9所示。

2.1? 縱搖運動受力分析

2.1.1? 浮子縱搖

先對整個垂蕩運動下的浮子進行分析，建立浮子的合外力矩和轉動慣量與角加速度的乘積的等式，浮子的轉動慣量表示為：

（7）

其中Σ1、Σ2、Σ3為浮子錐體表面積、柱體側面積、柱體上圓面積，ds為面積微元，ρf為面密度。

得到浮子的轉動慣量后，我們再去分析浮子在縱搖過程中受到的多種力矩。力矩分類如下：

（1）波浪激勵力矩Td。為周期性波浪震蕩產生的力矩設其表達式為Td=cosωt。

（2）靜水恢復力矩TF。其大小與浮體相對于靜水面的轉角成正比，比例系數稱為縱搖靜水恢復力矩系數，該力矩的表示公式為：

TF=-Cθ

其中C為縱搖靜水恢復力系數，θ為浮體相較于靜水面的轉角。

（3）興波阻尼力矩TX。興波阻尼力矩與搖蕩運動的角速度成正比，方向相反，比例系數稱為縱搖興波阻尼系數，力矩的表達式為：

TX=-Gθ

其中G為縱搖行波阻尼系數。

（4）浮子的重力力矩Tg，根據受力分析可以看出在求解重力力矩前需要先把浮子的重心位置找到，重心位置Zg：

（8）

我們可以將重力矩的大小表達出來：

（9）

扭轉彈簧和扭轉阻尼器所構成的PTO系統產生的力矩TPTO。

（5）振子重力矩對浮子產生的“反作用”力矩To1，這里不能單一地把振子的重力矩取反，而是還要考慮到浮子相較于振子，振子的重心發生了變換，增加一個圓錐h的長度：

（10）

（6）浮子還存在振子的彈簧、直線阻尼器和靜水恢復力矩的反作用力矩Tx，如圖10所示。

2.1.2? 振子縱搖

（1）由扭轉彈簧和旋轉阻尼器所構成的PTO系統發生縱搖，并且該系統將會產生一個扭矩，可以看作是整個振子系統產生的轉動慣量：

（13）

其中Ωv為振子的垂蕩區域，ds為振子表面積的微元，ρv為振子的密度；?Z1為關于t的一個函數，且目標積分體積Ωv隨著t發生著改變。所以得到的振子轉動慣量Iv是關于t的一個函數。

振子的轉動慣量得到后，可求振子的轉動力矩TPTO：

（14）

N1為旋轉彈簧的剛度，K1為旋轉阻尼器的系數。

（2）振子也會產生一個重力力矩To，同理，在求解振子本身的重力力矩時，利用彈簧的伸長變換量找出振子的重心位置，振子的質量是均勻分布的，即重心的位置如圖11所示。

因振子本身質量很大，彈簧本身被其壓縮，故壓縮高度為Z0=mvg/N，此外振子本身有一個實際的位移?Z1，所以就得到了彈簧的伸縮量變化hs-Z0+?Z1，于是重心的位置： hs-Z0+?Z1＋（1/2）h0，所以振子的重力矩公式：

（15）

2.2? 縱搖運動模型

通過求出的力矩和轉動慣量再利用轉動定律可得振子縱搖運動模型：

（16）

同理得出浮子的縱搖運動模型：

（17）

3? 裝置實際運動模型建立

根據垂蕩與縱搖運動模型的結合，可以知道運動裝置完整的運動狀態，并得出浮子與振子的微分方程組：

（18）

（19）

已經得到了振子和浮子的運動方程情況下，先將二階微分方程組降階處理，我們取步長為stp=0.002來離散，代入4階的Rung-Kutta特解方程組將浮子與振子的垂蕩位移與速度和縱搖角位移與角速度求解出來，得出浮子與振子的運動模型，如圖12至圖15所示。

取第10 s，20 s，40 s，60 s，100 s的數據如表3所示。

4? 確定直線阻尼器的最優阻尼系數的數學模型

基于浮子做垂蕩運動基礎上，直線阻尼器在振子中做類似切割磁感線的作用（楞次定律），形成了機械能轉化成電能的過程。功率最大情況的計算，圓頻率即為波浪的頻率ω（角頻率）。此外還需要考慮縱搖運動產生的功率，兩種功率相加即為裝置最終輸出功率，并由此確定直線阻尼器的最大系數。由于存在轉動角微分的情況，故采用功微元法，利用積分來計算P=FV縱搖的輸出功率。

4.1? 直線阻尼器做功

由角速度公式：T=ω/2π，計算n個完整周期內直線阻尼器做功的情況。由于存在運動位移微分的情況，故采用功微元法，利用積分去求解做功 ，因為?s是關于t的一個函數，所以d=d/d（t）×d（t），又因為 ，所以求得垂蕩時阻尼器平均做功功率為：

（20）

4.2? 旋轉阻尼器做功

還是利用P=FV計算縱搖產生的輸出功率，F=TRDD， ，縱搖運動輸出的平均功率的積分方程則為：，代入? 后，得出：

（21）

由已求解出的阻尼器垂蕩運動輸出的平均功率表達式：

可得阻尼器輸出的總功率：

（22）

4.3? 最大功率與最佳系數

（1）將K1所在的區間[0， 100 000]和N1所在的區間[0， 100 000]分別進行步長為stp=100進行網格化操作，每個離散的Ki，N1i為Ki=（i-1）stp，（i=1， 2， 3，…，1 000），N1i=（i-1）stp，（i=1， 2， 3，…，1 000）。

（2）針對每一個Ki，Ni我們用Runge-Kutta法求出它所對應的振子和浮子的垂蕩速度。

（3）將得出的振子和浮子的垂蕩和縱搖速度代入? 中利用黎曼和方法算出輸出功率數值積分。

（4）挑出最大輸出功率所對應的最大阻尼系數。

前面的步驟我們用步長為stp=100從1 000個數據中粗濾，找到了最大輸出功率，現在我們將對區間[Ki-100， Ki+100]和[N1i-100， N1i+100]進行步長stp=1對上述（1）～（4）步驟進行精細搜索，得出最大輸出功率。

我們得出了阻尼系數K的最優解為3.763 5×104，旋轉阻尼系數N1最優解為2.458 5×105，且輸出功率最大為2.759 8×10124。

5? 結? 論

裝置利用波浪能做的垂蕩和縱搖運動進行詳細分析，在此基礎上，裝置內部產生的最大發電功率和相應部件參數的求解，同時提供一定的波浪能發電裝置的設計指標。主要結論有如下：

（1）裝置的外形設計是圓錐形和圓柱形的結合形成浮子，內部設計是中軸底座固定于隔層的中心位置，中軸架通過轉軸鉸接于中軸底座中心，中軸繞轉軸轉動，PTO系統（彈簧和直線阻尼器）連接振子和轉軸架，并處于中軸與轉軸所在的平面。除了直線阻尼器，在轉軸上還安裝了旋轉阻尼器和扭轉彈簧，直線阻尼器和旋轉阻尼器共同做功輸出能量。

（2）裝置的最大輸出功率為2.759 8×10124以及產生最大功率時的直線阻尼系數為3.763 5×104和旋轉阻尼系數為2.458 5×105。

參考文獻：

[1] 馬哲.振蕩浮子式波浪發電裝置的水動力學特性研究 [D].青島：中國海洋大學，2013.

[2] 王凌楓.垂蕩浮子式波能轉換裝置水動力性能研究 [D].大連：大連理工大學，2016.

[3] 姜楠，劉聰，張蕭，等.波浪能俘獲裝置的設計和研究 [J].太陽能學報，2022，43（8）：447-451.

[4] 陳佳，蘭飛，郭昊霖等.波浪能發電控制技術研究綜述 [J/OL].電力自動化設備：1-20[2022-09-10].https：//doi.org/10.16081/j.epae.202208025.

[5] 謝惠媚，孟凡泰，徐潛龍，等.不同形狀的多自由度內置PTO式波浪能轉換裝置的性能分析 [J].可再生能源，2022，40（7）：986-994.

作者簡介：羅焙琢（2001—），男，漢族，四川眉山人，本科在讀，研究方向；大數據分析；羅洋洋（2001—），男，漢族，四川射洪人，本科在讀，研究方向；機器學習；楊亞洲（2005—），男，漢族，四川成都人，本科在讀，研究方向：近海海洋動力環境觀測與模擬。

收稿日期：2022-10-11