基于阿基米德Copula的極尾相依Copula的漸近展開①
廖娟, 彭作祥
西南大學 數學與統計學院,重慶 400715
連接函數Copula[1]可以將多個邊緣分布函數結合成一個聯合分布函數, 其中邊緣分布是隨機變量的分布, 因此可以借助連接函數來刻畫變量之間的相依關系. 關于Copula函數的性質及其應用的更多研究, 見文獻[2-4].
Copula函數族中有種類眾多的Copula函數, 包括阿基米德Copula、 橢圓Copula、 極值Copula等. 阿基米德Copula是一種性質優(yōu)良的Copula函數, 具有構造簡單、 計算容易且便于應用的優(yōu)點.

(1)
則稱Copula
C(x,y): =ψ[-1](ψ(x)+ψ(y))
(2)
為阿基米德Copula且函數ψ是C的生成元. 當ψ(0)=∞時, 則稱生成元ψ和其對應的阿基米德Copula是嚴格的[5].
(3)
利用Copula可以解決許多重要問題, 其中就有極值問題. 極值理論需要估計比以往所觀測到的現象更極端的事件的發(fā)生概率, 因此引發(fā)了對條件隨機向量相依結構的研究. 文獻[7]提出了CopulaC在水平u的極尾相依Copula的概念.
對于一個CopulaC并且u∈(0, 1)使得C(u,u)>0, 令
(4)
關于C在水平u的極尾相依Copula為
(5)


文獻[10-13]討論了正規(guī)變換函數和二階正規(guī)變換函數, 用以研究某個估計量的收斂速度, 本文討論生成元ψ在原點處滿足二階正規(guī)變換的條件下, 即ψ∈2RV-α,β(0+), 其中
(6)
輔助函數A(t)是定號的(見文獻[14]), 得到極尾相依CopulaCu的漸近展開.
1 漸近展開式

Cu(x,y)=CCl,α(x,y)(1+o(A°ψ-1(2ψ(u))))(1+B(u)(1+o(1)))
(7)
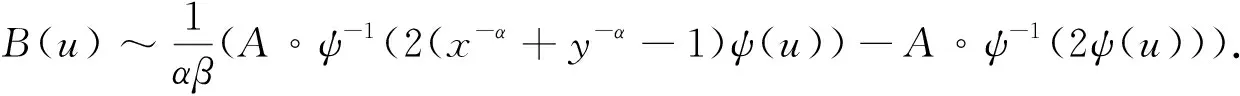
證對于生成元為ψ的阿基米德CopulaC, 由文獻[7]命題3.2知
(8)
且根據(2),(5)和(8)式, 有
令k=ψ-1(2ψ(u)), 那么
(9)
由ψ∈2RV-α,β(0+), 0<α<∞,β>0, 輔助函數為A(t)可得
(10)
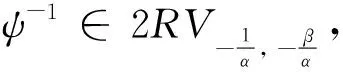
(11)

(12)

(13)

其中, 令
則有
Cu(x,y)=CCl,α(x,y)(1+o(A°ψ-1(2ψ(u))))(1+B(u)(1+o(1)))

定理證畢.
2 實例
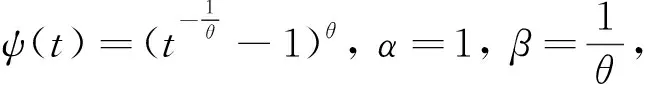
(14)
將ψ和ψ-1的具體表達式代入(14)式, 令
則有

并且
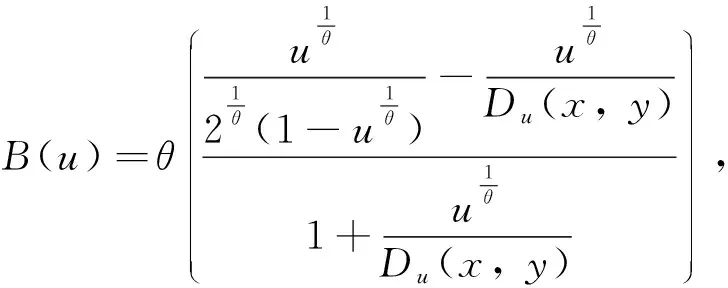
且
Cu(x,y)=CCl,α(1+o(A°ψ-1(2ψ(u))))(1+B(u)(1+o(1)))
與定理的結論一致.
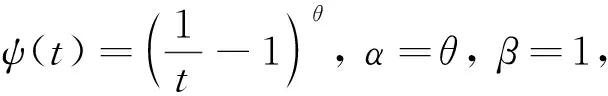
(15)
令
將ψ和ψ-1的具體表達式代入(15)式得

并且,
令

且
Cu(x,y)=CCl,α(1+o(A°ψ-1(2ψ(u))))(1+B(u)(1+o(1)))
與定理的結論一致.

