基于指數平方損失的縱向多折點回歸模型的穩健估計與統計推斷①

唐銘， 李婷婷

西南大學 數學與統計學院，重慶 400715

折點回歸模型主要研究響應變量與協變量間的分階段連續變化特征, 在金融、 經濟、 工業、 醫學等領域有著重要應用． 文獻[1]首次提出單折點回歸模型, 并基于似然函數提出折點參數估計的網格搜索法． 文獻[2]基于累積和統計量及似然比統計量提出折點效應的假設檢驗方法． 值得一提的是, 文獻[1]所提的網格搜索法雖然可以生成合理的估計, 但計算成本卻很高． 文獻[3]基于泰勒展開提出了一種局部線性平滑的參數估計方法, 在保證估計準確性的同時極大提高計算效率． 文獻[4]首次將單折點回歸模型拓展到多折點回歸模型, 基于局部線性平滑法提出了分位數損失函數下的參數估計、 變點存在性檢驗統計量, 及折點個數確定的貝葉斯信息準則, 并研究了所提估計及統計量的大樣本性質．

以上文獻的研究大多討論的是獨立同分布數據的折點模型． 然而, 隨著應用領域的不斷拓展, 所處理的數據類型越來越復雜, 縱向數據便是復雜的數據類型之一． 針對縱向折點回歸模型, 文獻[5]在獨立工作矩陣下考慮了縱向單折點分位數回歸模型的估計與檢驗; 文獻[6]考慮了縱向數據的多折點分位數回歸模型． 為融合縱向數據同一個個體內部的相關性, 文獻[6]基于文獻[7]提出的二次推斷函數方法(quadratic inference function, QIF)研究了相關結構下縱向多折點分位數回歸模型的估計與統計推斷, 但其所能刻畫的仍是等相關和AR(1)等特殊結構的矩陣． 文獻[8]提出修正的Cholesky分解方法, 該方法不局限于特殊相關結構, 且能保證估計的協方差陣的正定性, 具有更廣泛的適用性．

眾所周知, 基于經典平方損失的估計對異常值非常敏感． 為處理包含大量異常值的數據, 眾多穩健估計的方法被相繼提出, 如Huber損失函數法[9]、 秩回歸[10]及分位數回歸方法[11]等． 文獻[12]提出一種新的穩健估計方法, 即基于指數平方損失函數的參數估計方法． 該方法的顯著特征是引入一個額外的調諧參數, 可通過選擇合適的調諧參數實現模型參數的自適應穩健估計． 文獻[13-15]關于指數平方損失函數的相關研究均表明, 基于該損失的參數估計相對于經典的穩健方法有著更好的表現, 能夠獲得更好的魯棒性和有效性．

本文基于指數平方損失和修正的Cholesky分解方法研究縱向多折點回歸模型的參數估計及統計推斷．

1 模型與估計算法

1.1 縱向多折點回歸模型

考慮折點個數K及折點位置τ=(τ1, …,τK)T均未知的縱向多折點回歸模型:

(1)

其中:n為個體數,mi為第i個個體的重復觀測次數, (a)+=a·I(a≥0),I為示性函數,Yij為響應變量觀測值,Zij為p維協變量觀測值,Xij為有界門限變量,eij為隨機誤差, 記ei=(ei1, …,eimi)T． 由模型(1)可知, 變量Xij的回歸系數在折點τ=(τ1, …,τK)T處會發生變化． 記b=(b1, …,bK)T, ?= (a0,a1,bT,βT)T, 以及參數向量θ= (?T,τT)T, 其中?∈G?R2+K+p,τ∈T?DK．G,T均為緊集,D為Xij的支撐集． 下面, 首先對假設折點個數K已知后的參數估計算法進行介紹, 隨后給出用于確定折點個數K的模型選擇方法．

1.2 基于指數平方損失的縱向多折點回歸模型的參數估計算法

(2)

進而有如下的近似回歸模型

(3)

(4)

(5)

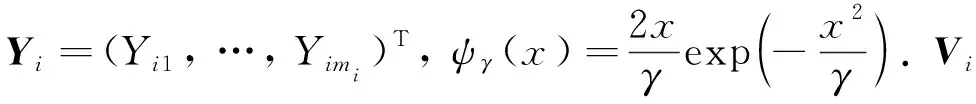
(6)

其中Φi是主對角線元素全為1的下三角矩陣, 第(j,k)個元素是如下自回歸方程系數φijk,γ的相反數

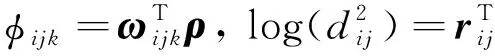
(7)

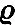
(8)

其中

本文使用Newton-Raphson迭代算法求解方程組(8)以保證估計的精度． 下面給出在指定調諧參數γ下, 基于指數平方損失的縱向多折點回歸模型的參數估計算法:

步驟1給定初始折點位置τ(0), 計算模型(3)的普通最小二乘估計作為η的初始值η(0)．

步驟2基于τ(s)及η(s), 應用修正的Cholesky分解法估計協方差陣Vi, 使用Newton-Raphson算法迭代求解方程組(8)獲得η(s+1), 具體步驟如下:

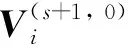
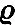
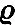
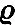
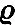
步驟2.2.3根據(6)式及(7)式, 可得Vi, r+1． 通過下式迭代至收斂得到η(s+1, r+1):

步驟2.3重復步驟2.2直至參數收斂, 可得η(s+1)．

步驟3更新折點位置τ(s+1)． 通過

(9)

步驟4重復步驟2-步驟3直至參數收斂．

注1當Vi為單位陣時, 方程(5)和最小化目標函數(4)的解等價． 因此, 在上述步驟中省略步驟2.2.1及步驟2.2.2, 設置步驟2.2.3中Vi, r+1為單位陣, 即可獲得獨立工作矩陣情況的參數估計．

1.3 最佳調諧參數γopt的選擇

1.4 折點個數K的確定

1.2節給出了當折點個數給定的時候模型參數的估計算法． 然而實際問題中, 折點個數真值K0通常是未知的． 參考文獻[4], 提出如下基于指數平方損失的貝葉斯準則以確定折點個數:

(10)

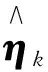
2 大樣本性質

(11)

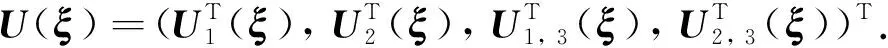
給出如下條件:

(ⅰ) E(ψγ(eij))=0, E(ψ′γ(eij))>0, 且對于任意γ>0, E(ψγ(eij)2)有界．

(ⅱ) 折點的真值K0及協變量Zij的維數p是固定的, 個體的觀測次數mi一致有界, 且個體數n趨于無窮．

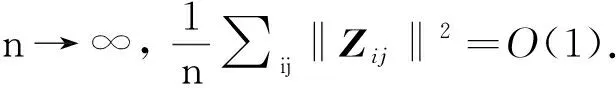
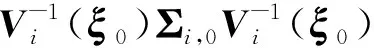
(ⅵ) 參數空間Θ∈R2+p+2K是緊集, 參數真值η0是參數空間Θ的內點,Sn(η)在η0處唯一取得全局最小值．

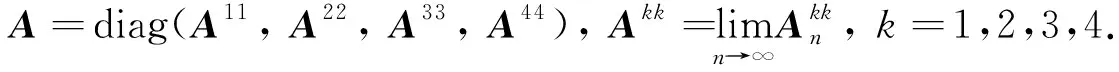
(12)

其中

(13)

(14)

3 折點的存在性檢驗

對于多折點回歸模型的折點存在性檢驗, 文獻[4]基于無折點的原假設H0:bk=0,k=1, …,K提出CUSUM(cumulative summation)型統計量． 本文沿用文獻[4]所提方法, 提出基于指數平方損失的縱向折點回歸模型的折點存在性檢驗方法, 具體步驟如下:

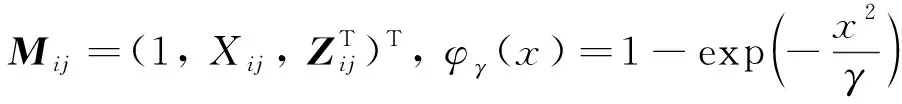
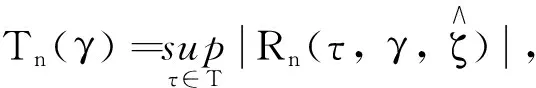
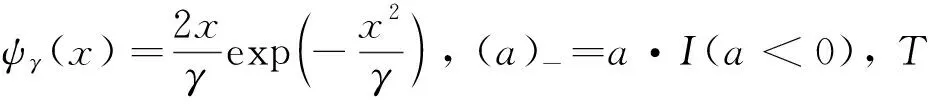
步驟4重復步驟3L次, 計算

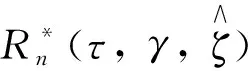
4 模擬研究

根據如下模型生成數據

(15)

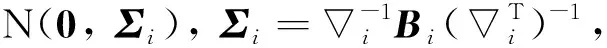
情形2 考慮門限變量不為時間, 且數據存在異常值的情況． 設置Xij～U(-5, 5),tij={1, 2, …, 10}, 隨后每個觀測以20%的概率缺失以生成不平衡數據．ei服從自由度為3, 協方差陣為情形1中Σi的多元t分布, 隨后隨機選取10%的eij服從標準柯西分布．

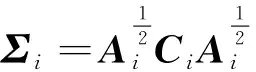
每種情形均考慮3種折線效應, 對于情形1, 設定: ①K=1,τ=7, ?=(-2, 1, -3, 1)T; ②K=2,τ=(5, 7)T, ?=(2, 1, -4, 5, 1)T; ③K=3,τ=(2, 5, 7)T, ?=(0 , 1 , -3 , 2 , -6 , 1)T． 對于情形2、 3, 系數?設置與情形1相同, 折點個數和位置設置為: ①K=1,τ=-1; ②K=2,τ=(-1, 1)T; ③K=3,τ=(-4 , -1 , 4)T． 設定樣本量n=400, 重復模擬次數為100次． 使用1.2節所提算法求解最小化目標函數(4)及方程組(8), 分別記為“ESL．IND”和“ESL．CHO”, 即獨立工作矩陣結構及基于Cholesky分解的模型參數的估計方法．

4.1 最優調諧參數γopt的選擇

表1給出3種情形下所有模擬中選擇的最優參數γopt的均值． 可以看到, 無異常值的情形下,γopt均值較大; 情形2,3的γopt較小, 以降低異常值產生的影響． 這說明在指數平方損失函數中, 可以通過選擇合適的調諧參數實現回歸系數的自適應穩健估計．

表1 最優調諧參數γopt的均值

4.2 選擇相合性及參數估計

表2給出了真實折點個數為2時, 不同Cn在3種情形下的折點個數的正確選擇率． 可以看到, 所有情形下, 本文所提出的折點個數選擇方法均具有較高的正確選擇率, 并且“ESL.CHO”能夠實現更高的選擇正確率． 而且樣本量不變時, 較大的Cn能略微提高正確選擇折點數的概率．

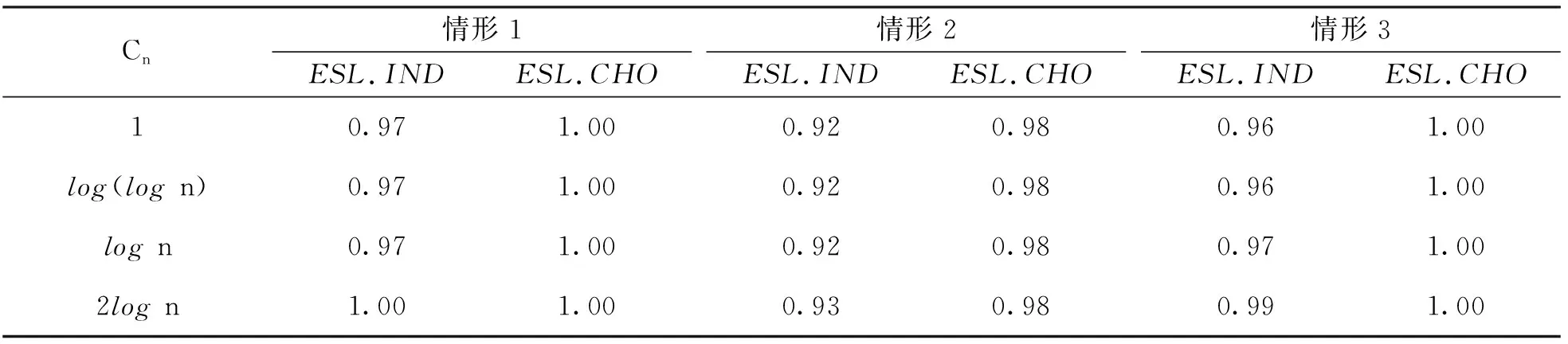
表2 K=2, Cn=1, log(log n), log n, 2log n時的折點個數正確選擇率

為說明所提方法優勢, 與以下估計量進行比較:

1) 方程(5)的工作協方差矩陣Vi為等相關及AR(1)的特定結構, 利用文獻[7]提出的QIF方法對(5)式進行求解, 同時分別考慮指數平方損失及經典的平方損失兩種損失函數, 記所得估計量分別為“ESL．EXCH”“OLS．EXCH”“ESL．AR1”“OLS．AR1”;

2) 文獻[4]提出的基于分位數回歸的縱向多折點模型的估計量, 指定分位水平為0.5, 記為“MKQR”, 使用R程序包MultiKink實現;

3) 文獻[3]提出的多折點模型的最小二乘估計量, 記為“SEG”, 使用R程序包segmented實現．

表3展示了情形2在K=2時的參數估計結果, 匯總了100次模擬中估計量的平均偏差、 標準差及均方誤差． 其余情形的參數估計的結果已上傳至Github(https: //github．com/Tangming-hub)． 可以發現:

表3 情形2, K=2的模擬結果

1) 當殘差向量服從正態分布時(情形1), 幾種方法所得到的估計量的估計效果相近． 然而當數據中存在異常值時(情形2和情形3), 基于指數平方損失和分位數回歸的估計量“ESL．IND”“ESL．CHO”“ESL．EXCH”“ESL．AR1”和“MKQR”均能提供回歸參數的有效估計, 其中相對于分位數回歸方法, 基于指數平方損失函數的估計量表現更佳, 而基于經典的平方損失函數的估計量的估計效果均較差;

2) 僅考慮指數平方損失函數的估計方法時, 相對于獨立工作矩陣的估計量“ESL．IND”, 融合組內相關性的估計量“ESL．CHO”“ESL．EXCH”“ESL．AR1”均具有更優良的估計效果, 且本文所提出的“ESL．CHO”在各指標上表現最佳． 這說明有效考慮縱向數據個體重復觀測有利于提高回歸參數的估計效率． 綜上, 本文所提出的估計方法, 可以為縱向多折點回歸模型的參數提供更為穩健的、 有效的估計．

此外, 不同情形下K=2時, 3種估計方法“ESL．CHO”“ESL．IND”“MKQR”的標準差、 標準誤、 95%的 Wald型置信區間的平均長度及經驗覆蓋率亦上傳至Github． 由結果可見, 3種估計量的標準差與經驗標準誤差接近, 并且所構造的置信區間的經驗覆蓋率均在置信水平95%左右． 并且, 相對于“MKQR”方法, 本文所提方法的置信區間的長度更短．

4.3 折線效應存在性檢驗的功效性分析

為研究本文第3節所提出的折線效應存在性檢驗統計量Tn的有限樣本性質, 考慮折點個數為2時檢驗統計量的功效． 對于情形1, 設置-b1=b2=0,0.1,0.2,0.3; 對于情形2和情形3, 設置-b1=b2=0,0.15,0.3,0.45, 其中當系數b1和b2都等于0時, 不存在折線效應． 設置L=300, 顯著性水平α=0.05． 表4展示所得檢驗統計量均值(Mean ofTn, 簡記為Mean-Tn)及經驗p值(Power)． 根據統計量的定義, 當原假設成立時, 統計量Tn應接近于0, 模擬結果與理論一致． 注意到, 當折線效應不存在時, 經驗P值接近名義上的顯著性水平0.05, 而隨著折線效應增強, 檢驗功效增加, 并趨近于1, 這說明本文提出的檢驗統計量能夠有效識別折線效應．

表4 K=2時各情形在不同折線效應下統計量Tn均值及檢驗功效的勢

本文亦使用所提方法“ESL．IND”“ESL．CHO”分析文獻[4]的縱向黃體酮數據, 參數的估計值、 平均絕對誤差、 置信區間, 以及擬合曲線(結果見Github)． 實證結果顯示, 相較“SEG”“MKQR”方法, 所提估計具有明顯競爭優勢．

5 證明

為了證明定理1, 我們給出如下引理．

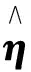
(16)

(16)式等價于

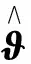
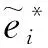
以及

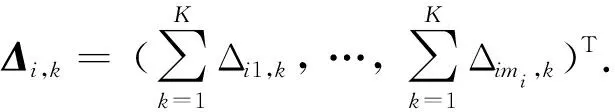
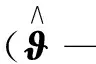
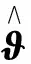
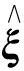
(17)

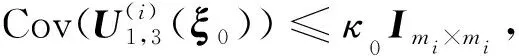
(18)

結合(17)式及(18)式,

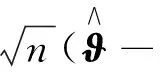
故而定理1可證．

定理2的證明記折點位置真值為τ0=(τ1, 0, …,τK,0)T． 由(9)式可得等式

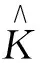
經計算,

定理3得證．

6 總結

本文基于指數平方損失提出縱向多折點回歸模型參數估計和統計推斷方法． 為處理折點回歸模型, 本文首先基于局部線性平滑方法將折點回歸模型轉化為普通的縱向線性模型． 然后為融合縱向數據中重復觀測間的相關性, 本文利用修正的Cholesky分解方法對重復觀測間的協方差陣進行建模, 以提高回歸模型參數的估計效率． 本文討論了參數估計的大樣本性質, 并同時討論了指數平方損失函數中調諧參數的選擇、 折點個數的確定方法和折線效應的檢驗問題等． 數值模擬和實證分析結果顯示本文所提方法可以為縱向多折點回歸模型的參數提供更為穩健的、 有效的估計．