基于超單元法的無鉸式旋翼槳轂動力學等效參數計算方法
邱志祥,喻國瑞,王偉特
(中國直升機設計研究所,江西 景德鎮(zhèn) 333001)
0 引言
旋翼動力學分析中的動力學參數即為結構的力學參數。將旋翼簡化為梁模型的經典氣彈分析方法中,需輸入槳葉剖面特性、槳轂剖面特性和操縱線系剛度等參數。
無鉸式旋翼動力學特性對槳轂剖面特性較為敏感,同時槳轂支臂中多采用金屬軸承,包含復雜的接觸和約束問題,旋翼動力學建模時采用面積分的槳轂結構剖面特性參數會造成旋翼動力學計算結果偏差較大。國外在處理類似槳轂支臂梁模型參數時,通過引入三維有限元思想,獲取槳轂支臂等效剛度特性[1]。
本文提出一種計算槳轂等效動力學參數的計算方法:首先對靜力縮聚超單元法等效計算槳轂支臂動力學參數開展理論分析,推導等效剛度計算公式和誤差;其次基于實際模型,對槳轂支臂進行三維有限元建模,給出軸承的簡化處理辦法,開展模態(tài)分析,驗證靜力縮聚超單元法的可行性;最后對槳轂支臂進行三維有限元靜力分析,根據分析結果,對三維結構進行縮減,獲取槳轂支臂揮舞剛度和擺振剛度兩個動力學參數。旋翼旋轉動特性試驗結果表明,該等效方法計算精度滿足工程所需。
1 超單元基本理論推導
超單元法是將各子結構內部自由度縮聚到邊界自由度上,然后將子結構的獨立邊界自由度進行組合求解。常用的超單元法分為三種:靜力變換超單元法、定頻動力變換超單元法、模態(tài)綜合超單元法[2-3]。其中,靜力變換超單元法強制忽略了內部自由度,會導致高階振動分析產生較大誤差。當關注的頻率成分遠小于子結構模態(tài)頻率,靜力變換超單元法可大大降低模型分析的復雜度。圖1為子結構示意圖。

圖1 子結構示意
如圖1,假設子結構1是復雜結構,內部多路傳力,且包含非線性接觸約束,不能直接看成單梁結構。使用有限元技術,將結構離散,設總共有N個自由度。將N個自由度進行區(qū)分,分成子結構1邊界上的自由度(下標m)和非邊界上的自由度(下標s)。則可以將子結構1的動力學方程寫為:
⑴
對上述時域方程做傅里葉變換,可寫為頻域傳遞矩陣表達式:

(2)
根據上式有:
DsmXm+DssXs=0

(3)
將式(3)帶回式(2),可得
(Dmm+DmsT)Xm=Fm
令:P=Dmm+DmsT
由此可將式(1)變換為
PXm=Fm
(4)
上述為超單元法的基本理論,式(4)稱為超單元方程,P為超單元動力矩陣。根據該基本理論,為完全等效不具有梁特性的子結構1(槳轂),就需要通過槳轂的三維實體,建立有限元模型,再生成2節(jié)點超單元梁模型即可。
將超單元方程轉換至模態(tài)坐標系(Φ為模態(tài)振型,ξ為模態(tài)坐標),此時子結構動力學方程如下:
ΦT(K-ω2M)Φξ=ΦTFm
(Kdiag-ω2Mdiagξ=Fξ
(5)
結構固有頻率

(6)
最終動力學方程描述如下

(7)

本文所采用的靜力縮聚超單元法,是在局部柔性不突出的情況下,子結構最低階模態(tài)固有頻率遠大于外載激勵最高頻率。此時P可退化成剛度等效矩陣,因此超單元法的實現流程可轉化為對槳轂支臂整體靜剛度的等效過程。圖2給出了基于上述超單元法理論制定的獲取槳轂動力學參數的技術路線。

圖2 槳轂動特性參數獲取技術路線
2 槳轂支臂三維有限元分析
圖3給出了某萬向鉸旋翼槳轂支臂示意圖,槳轂支臂由槳葉連接件、軸頸螺母、三組軸承和槳轂中央件組成。離心力沿槳葉連接件、軸套螺母、鉸接觸軸承3、推力軸承2、深溝球軸承1、軸頸螺母、中央件支臂路徑傳遞(圖中軸承區(qū)域,黑色代表滾珠,同色兩部分結構分別代表軸承內外圈)。彎矩傳遞路徑有兩條:一是通過軸承1和軸承3的剪力承擔,二是通過軸承2軸向非均布壓力承擔。
2.1 三維有限元建模
經過分析槳轂支臂傳力路徑方式,保留其承力主體結構,包括槳轂中央件、槳葉連接件、三個軸承以及相應兩端的緊固件。
實際軸承包含內圈、外圈、滾動體等承力組件,滾動體和內外圈之間滿足Hertz接觸理論,可通過三維有限元建立軸承詳細分析模型[4-5]。但上述軸承模型復雜,不適合槳轂支臂整體分析。本文關注槳轂支臂整體剛度特性,不關注軸承局部受力情況,為提升建模和計算效率,給出了一種軸承簡化處理辦法。圖4給出了軸承簡化模型,滾動體簡化為圓柱形實體結構,圓柱側面積為軸承滾道投影區(qū)域。根據軸承傳力特征,滾動體等效結構一側與軸承內圈或外圈融合,另一側設置摩擦接觸約束。圖5給出了軸承內外圈與槳轂支臂內部其他相鄰結構的約束關系,根據傳力特征分別選擇Tie約束或者接觸摩擦約束。在槳葉連接件襯套孔中心施加彎矩,固支約束槳轂中心,最終有限元模型如圖6。

圖4 槳轂支臂內部軸承等效建模

圖5 槳轂支臂內部接觸約束示意圖

圖6 槳轂三維有限元模型
2.2 固有頻率計算
圖7給出了上述槳轂支臂三維有限元模型模態(tài)分析結果,揮舞一階頻率24.92Ω,擺振一階頻率32.67Ω。
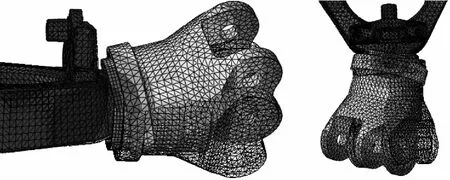
圖7 槳轂支臂模態(tài)分析結果
旋翼動力學設計關注前8階諧波影響。固支邊界條件下,將槳轂支臂整體靜剛度等效為動力學參數,子結構簡化分析誤差:
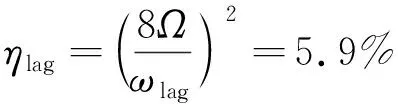
(8)
計算結果表明,揮舞一階頻率最低,等效剛度最大誤差為10.3%。
2.3 靜力分析和動力學參數等效
在上述槳轂支臂三維有限元模型的基礎上,對槳轂支臂進行靜剛度分析,計算出槳葉連接位置加載點處的變形θflap和θlag。采用靜力縮聚超單元法計算出的槳轂支臂等效揮舞剛度與擺振剛度如下:
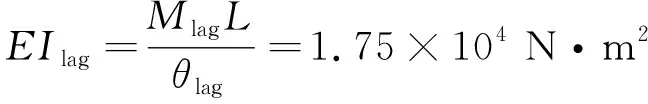
(9)
圖8給出了傳統面積分法和靜力縮聚法得到的槳轂剛度對比。可以看出,由于面積分是簡單將剖面各結構的剛度疊加,類似將結構視為并聯傳力,其計算的剖面剛度遠遠大于靜力縮聚計算結果。
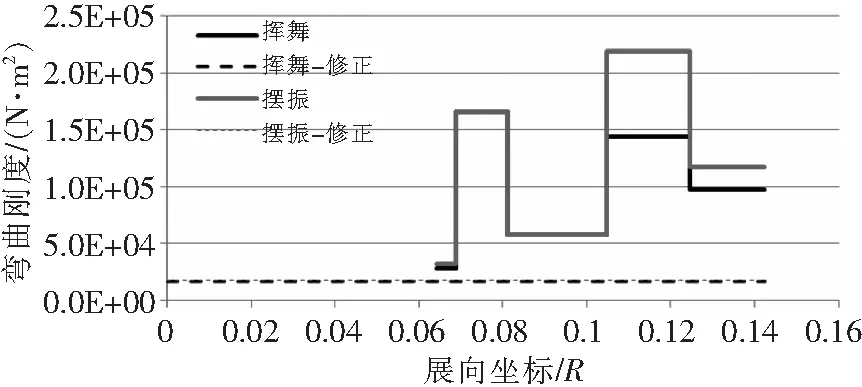
圖8 面積分法(實線)和靜力縮聚(虛線)得到的槳轂剛度對比
3 旋轉動特性試驗驗證
3.1 旋翼動特性計算
建立旋翼CAMRAD II計算模型,開展動特性計算。為簡化模型以適用于工程設計,將萬向鉸模型的槳根約束邊界等效為固支邊界和鉸邊界,前者對應揮舞集合型模態(tài),后者對應揮舞周期型模態(tài)。對于3片槳葉萬向鉸旋翼,揮舞集合型模態(tài)避開3、6、9……等槳葉片數整數倍諧波頻率,揮舞周期型模態(tài)避開1、2、4、5、7、8……等非槳葉片數整數倍諧波頻率[6]。
表1是中立總距、額定轉速狀態(tài)各階模態(tài)頻率比。計算結果表明,除揮舞周期型耦合一階相近,靜力縮聚法得到的其他各階模態(tài)頻率比都明顯小于面積分法。圖9是揮舞周期型共振圖。結果表明,兩種方法揮舞周期型耦合二階模態(tài)與2Ω的共振點分別為85% RPM和63% RPM。

表1 中立總距狀態(tài),旋翼動特性計算結果

圖9 孤立旋翼動特性(揮舞周期型)
3.2 旋轉動特性試驗
開展旋轉動特性試驗,通過發(fā)動機啟停識別工作狀態(tài)主旋翼模態(tài)[7]。圖10給出了槳葉不同剖面站位處揮舞貼片信號中二階諧波成分隨轉速的變化規(guī)律,結果表明在65%額定轉速附近存在共振。結合圖11揮舞周期型耦合二階槳葉振型圖以及旋翼共振圖,判斷該共振為揮舞周期型耦合二階與2Ω重合導致。試驗結果與靜力縮聚計算結果(63%額定轉速)吻合,說明了使用靜力縮聚計算槳轂動力學參數的有效性。

圖10 旋翼槳葉不同剖面揮舞信號二階諧波幅值隨轉速變化

圖11 揮舞周期型耦合二階槳葉振型圖
4 結論
本文給出了無鉸式槳轂支臂動力學參數的一種基于超單元法的靜力縮聚等效計算方法。核心是當槳轂支臂局部模態(tài)頻率遠大于關注的外載激勵最高頻率時(彈性力影響遠大于慣性力),可將結構剛度陣近似為超單元動力矩陣。該方法可以將包含復雜摩擦、接觸問題的三維槳轂支臂,通過三維有限元分析等效為一維梁,快速得到滿足工程使用的槳轂動力學參數。
該方法還可推廣至無軸承旋翼槳轂和其他類似非單梁復雜傳力構型槳轂上,為獲取更加準確的槳轂動力學參數提供了一種新思路。

