大撓性航天器的模糊模型預測控制*

管 萍,黃明亮,戈新生,曹彧騰

北京信息科技大學自動化學院,北京 100192

0 引言

新一代航天器通常需要配備各種大型的撓性附件,與之前的常規航天器的撓性器件相比,大型撓性附件具有體積大、質量小、模態頻率低且密集等特性,降低了負載指向精度,嚴重影響了航天器姿態控制的穩定性。故針對大型撓性航天器設計具有高精度、強魯棒性和高穩定性的姿態控制策略是當前需要解決的難點問題之一[1]。

近年來,國內外學者們已將魯棒控制、自抗擾控制以及容錯控制等多種控制方法應用于撓性航天器中,獲得了較好的控制效果[2-4]。然而,所研究的航天器均是撓性附件的質量和轉動慣量在整星中占比較小的常規撓性航天器,中心剛體的運動受到撓性附件振動的影響較小。對于撓性附件的轉動慣量和質量占整星的比重較大的大型撓性航天器高精度的三軸姿態控制,當前還鮮少有相關的研究。由于模型預測控制(model predictive control, MPC)的執行過程中引入了多步預測、滾動優化和反饋校正等多種控制策略,因此MPC有對模型的精確性要求不高和魯棒性強的特性,為有效解決不確定性和擾動及各種約束的控制問題提出了良好的解決方法,目前MPC已經被廣泛應用于化工、發電、航天等領域。近年來,已有學者將MPC算法應用在四旋翼飛行器、機器人軌跡跟蹤等航空航天領域中,并取得了一些成果[5-7]。

相對于常規撓性航天器,大撓性航天器的撓性振動模態頻率更低更密集,撓性附件的振動會引起系統未知的擾動,嚴重影響系統的姿態控制精度,甚至會破壞系統的穩定性。自適應模糊控制可以在整個控制過程中自適應地調整控制器的參數,從而逼近系統中的不確定量。文獻[8]設計出一種基于模糊控制估計系統參數的自抗擾控制和模型預測控制的復合控制方法,可實現永磁同步電機的無速度傳感器的運行。文獻[9]提出了一種新型模糊控制算法,控制吸氣式高超聲速飛行器對高度和速度指令的穩定魯棒跟蹤。文獻[10]設計了一種自適應模糊控制方法對具有不確定性摩擦的機械臂系統的控制效果良好。目前已有一些學者將自適應模糊控制應用于永磁同步電機、飛行器和機械臂等[8-10]。自適應模糊控制能很好地抑制系統中的不確定性擾動。

基于以上分析,本文將模糊模型預測控制應用于大撓性航天器的姿態控制中。先設置性能指標,求出性能指標最小時的模型預測控制律。隨后,設計了相應的模糊控制器來逼近大撓性附件振動對姿態控制產生的未知擾動。對模糊規則參數的自適應律進行了推導,證明了姿態控制系統的穩定性,仿真結果驗證了所設計控制方法可以實現對姿態角期望值的迅速跟蹤,具有一定的魯棒性。

1 大撓性航天器的數學模型

本文的研究對象為裝有太陽帆板的大型撓性航天器,如圖1所示,總體結構由安裝在兩側的可轉動的橫向太陽帆板、中心剛體和旋轉軸構成。

基于哈密頓原理和全局模態方法構建大型撓性航天器模型,假設航天器到達軌道預定位置并已完成了定向對日,鎖定航天器本體與太陽帆板的相對偏轉角,忽略軌道動力學影響的動力學模型為[11]:

(1)

(2)

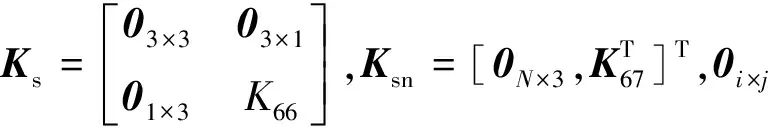
(3)

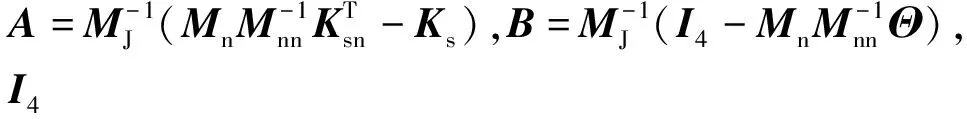
本文的控制目標為:在大撓性航天器系統(式(3))中,設計相應的模糊模型預測控制律,控制大型撓性附件振動快速衰減,使航天器的姿態角實現對期望值的迅速跟蹤。

2 模糊模型預測控制

針對大撓性航天器的姿態控制,首先,通過泰勒公式對系統(式(3))設計相應的模型預測控制律。然后在此基礎上,設計自適應模糊控制器逼近撓性振動產生的不確定擾動項D,以迅速衰減撓性振動,使航天器對姿態角指令迅速跟蹤。

2.1 模型預測控制律的設計

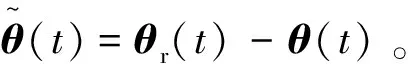
(4)

式中:可調時間參數T>0且控制參數λ>0。

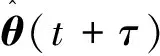
(5)

式中:

(6)

式中:

則性能指標(式(4))可近似寫為:

(7)

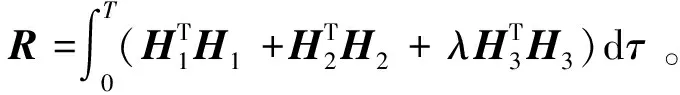
(8)

(9)

將式(9)代入到實際系統(式(3))中可得閉環系統方程:

(10)

根據K11和K12定義,可計算得

K11=42T2[25T8+4140T6+(218400λ+52416)T4+ 5019840λT2+25401600λ2]/K·I4

(11)

K12=52.5T[5T10+988T8+(56448λ+22032)T6+ (2028096λ+48384)T4+(13886208λ2+

4693248λ)T2+40642569λ2]/K·I4

(12)

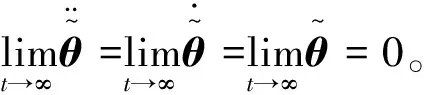
2.2 自適應模糊控制器的設計

在航天器運動過程中,安裝在航天器上的大撓性附件會產生劇烈的振動,嚴重降低航天器姿態穩定性。在此將撓性附件振動對姿態的影響視作擾動,采用自適應模糊控制來逼近撓性振動引起的擾動D。

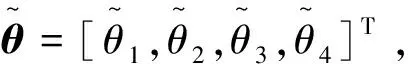
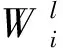
(13)

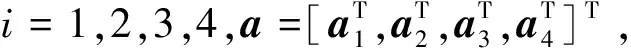
定義最優參數:

(14)

(15)

則由式(9)可得模糊模型預測控制律為:

(16)

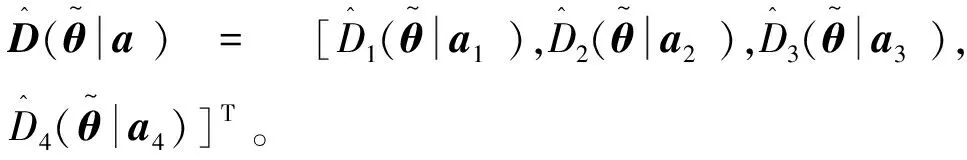
將模糊預測控制律(式(16))代入實際系統(式(3))中,可得:

(17)

故誤差方程為:

(18)

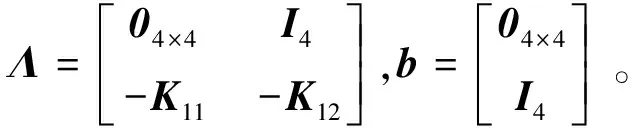
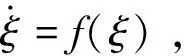
(19)

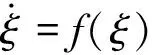
引理2[13]. 對實數變量z和實數變量ζ,任意大于0的常數μ,θ,ψ都存在:

(20)

定理1. 對于大撓性航天器姿態控制系統(式(3)),在模糊模型預測控制律(式(16))的作用下,模糊規則參數自適應律為:

(21)

式中:可調參數γi>0,則在有限時間內能使姿態誤差e收斂至0。

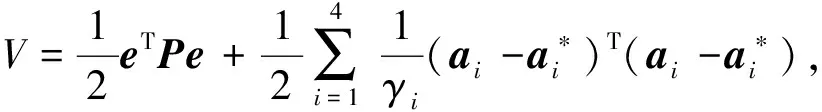
(22)

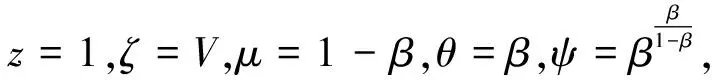
(23)

將式(23)代入式(22)中,可得:

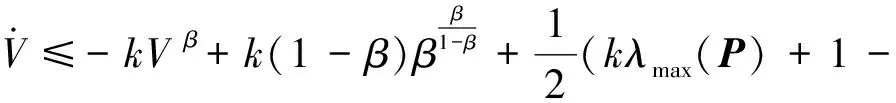
(24)

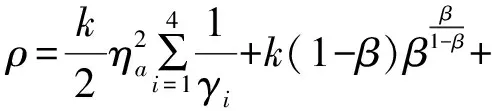
又因為k>0,0<β<1,由引理1可知,姿態誤差e在有限時間內收斂到0,證畢。

基于以上分析,本文的主要控制思想是首先基于泰勒公式近似預測量,從而求解最優問題得到非線性預測控制律(式(9))。其次用模糊控制逼近系統(式(3))中的擾動項D,并推導出了相應的自適應律(式(21))。

3 仿真校驗

將所設計的模糊MPC策略施加到大撓性航天器中,為了驗證控制策略的有效性,進行了數字仿真和結果分析。大撓性航天器的參數如下:中心剛體的質量mR=120 kg,考慮航天器具有四階模態的情況,即η=[η1,η2,η3,η4]T,中心剛體3個方向的轉動慣量J=diag(20,20,20) kg·m2,太陽翼長度L=8 m,寬度b=1 m,厚度h=0.01 m,其余參數詳見文獻[11]。

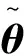
為進行比較,將所設計的模糊MPC策略和傳統MPC控制策略(文獻[5])分別應用在大撓性航天器的姿態控制上。姿態控制的仿真結果如圖2所示。在傳統MPC控制策略的控制下,大型撓性航天器的姿態角和太陽能電池帆板轉動角的響應時間分別為100 s、100 s、110 s和110 s,撓性模態η在200 s內還未趨于0。在模糊MPC控制策略的控制下,航天器三軸姿態角和太陽能帆板轉動角的響應時間均在80 s內,撓性模態η在100 s后趨于0。

在實際工程中,在空間運行時,大型撓性航天器太陽帆板的收縮和伸展會引起撓性附件的轉動慣量發生較大變化,從而導致航天器質量矩陣變化較大;同時航天器內部液體晃動、攜帶燃料的消耗等因素也會引起航天器的質量矩陣等參數發生變化,由此導致姿態控制系統的控制精度降低。故對質量矩陣Mx增加或減少20%的大撓性航天器姿態控制系統進行仿真驗證,以檢驗所設計控制策略的魯棒性。

當質量矩陣Mx增加20%時,姿態控制仿真結果如圖3所示。在傳統MPC策略的控制下,三軸姿態角和太陽能帆板轉動角分別在120 s、120 s、130 s和130 s內達到期望值,在200 s內撓性模態η還未趨于0;在模糊MPC控制器的控制下,航天器三軸姿態角和太陽能帆板轉動角均在80 s內跟蹤上期望值,撓性模態η在100 s后趨于0。質量矩陣Mx減少20%時的仿真結果與增加20%時相似,限于篇幅,此處未將仿真結果列出。

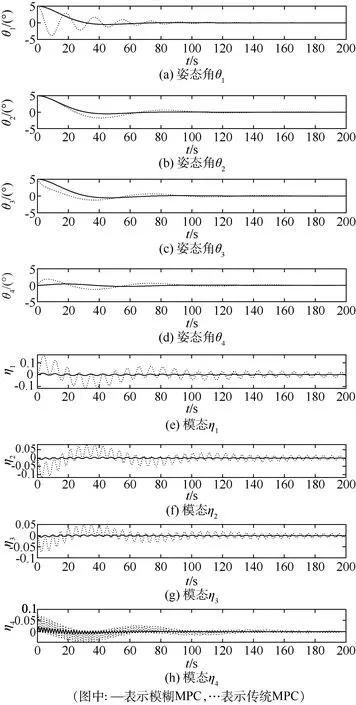
圖3 Mx增加20%時,姿態角、撓性振動模態響應曲線

仿真結果表明,傳統的MPC控制器能控制大撓性航天器的姿態角達到期望值,但其姿態角的響應時間較長,且撓性模態無法快速衰減趨于0。而本文設計的模型預測控制方法,通過泰勒公式求出了非線性預測控制律,進而有效地避免了由傳統MPC在線求解優化問題造成的繁重計算量。而自適應模糊控制可迅速逼近由大撓性附件的振動引起的不確定干擾,故所設計的模糊MPC能快速衰減大撓性附件的振動,使姿態角響應速度更快。在質量矩陣參數發生變化時,所設計控制方法的姿態響應時間能基本保持不變。

4 結論

針對撓性航天器的大撓性附件振動嚴重影響航天器姿態控制精度的問題,設計了模糊模型預測控制策略。通過使用泰勒展開求解性能指標的最優問題,設計出相應的非線性模型預測控制律,從而減少了在線計算量。采用模糊控制逼近撓性振動引起的不確定擾動,使撓性振動快速衰減。仿真結果表明,所設計的模糊模型預測控制策略可有效地抑制大撓性附件的振動,實現航天器對期望姿態角度的迅速跟蹤,具有較好的魯棒性。