一種三回路過載自動駕駛儀設計方法

陳中祥,韋漢林,任 韋,2

1. 江南機電設計研究所,貴陽 550009 2. 哈爾濱工業大學航天學院,哈爾濱 150001

0 引言

三回路過載自動駕駛儀結構因其具有良好的系統穩定性、快速性和魯棒性[1],廣泛應用于戰術導彈領域[2]。常用的三回路過載駕駛儀包括:偽攻角反饋駕駛儀和經典的Raytheon三回路駕駛儀。其中,經典的Raytheon三回路駕駛儀是由Raytheon公司為應對其雷達導引頭尋的制導回路設計而首次提出,因該結構不受氣動變化的影響,對高頻噪聲有較強的濾波能力,并可以減低雷達導引頭天線罩折射誤差斜率對制導回路的影響,而得到廣泛的應用。文獻[3]指出了該經典三回路自動駕駛儀頻域設計方法,通過指定控制系統期望的時間常數τ,阻尼ζ,開環截止頻率ωCR,求解閉環系統二階固有頻率,實現對閉環系統的極點配置,但是,其設計過程未考慮到控制系統期望指標的工程約束條件,導致當系統開環截止頻率ωCR不滿足遠大于彈體固有頻率時,其設計結果在工程實際中存在較大誤差。文獻[4]在文獻[3]的基礎上,提出的極點配置設計方法考慮了舵機動態特性等工程實際約束的影響,通過系統參數尋優實現了考慮舵機動態特性的極點精確配置,但是其設計過程未考慮系統開環截止頻率及最大舵偏角速度約束。文獻[5]提出了經典三回路過載自動駕駛儀設計不應以自振頻率為主要設計指標,而應以系統開環截止頻率約束為主要設計指標的思想,并給出了相關設計方法,但是其設計過程仍未能充分考慮最大舵偏角速度約束。

而偽攻角反饋增穩回路因采用偽攻角反饋,可以消除經典三回路駕駛儀的靜差,同時能保留較好的時域、頻域響應特性及魯棒性能,因此,在戰術導彈上得到廣泛的應用[6]。文獻[7]指出了以系統開環截止頻率為主要設計指標的駕駛儀設計方法,該方法的實際設計結果與期望指標一致性較好,但是其設計過程未考慮相位裕度、舵偏角速度等相關工程約束。文獻[8-9]指出了偽攻角反饋自動駕駛儀的極點配置設計方法,通過建立控制增益與閉環極點、開環截止頻率的解析關系式,考慮系統高頻部件約束、舵偏角速度約束及相位裕度約束,并基于Butterworth濾波器提出“共圓準則”,增加在同樣開環截止頻率及阻尼條件下,最小化閉環系統等效時間常數實現偽攻角反饋形式下,考慮開環截止頻率約束的極點配置方法。其設計的期望截止頻率與實際截止頻率差異較小,但是因部分彈體模型采用了近似性計算導致相位裕度具有一定的保守性。

綜上,當前三回路過載自動駕駛儀設計中,對于如何在充分考慮工程實際中舵偏角速度、開環截止頻率、相位裕度以及高頻部件等的約束條件下,完成參數的最優化、精確化設計仍需要開展相關研究。本文首先從常用的三回路過載駕駛儀的模型出發,統一給出系統開環傳遞函數與閉環系統特征方程的關系,然后依據閉環傳遞函數確定系統控制增益與閉環極點、開環截止頻率的關系,通過引入舵偏角速度約束、開環截止頻率、穩定裕度指標約束,高頻部件約束,進而給出最小化閉環系統等效時間常數的目標函數,形成典型的約束條件下參數尋優范式,通過求解系統最優解,實現系統開環截止頻率、相位裕度的精確設計,形成一種可工程化的設計方法。

1 彈體縱向運動方程

導彈是一個時變、非線性的彈性結構體,通常將戰術導彈視為剛體。利用小擾動線性化方法,對彈體縱向運動方程進行簡化,得到便于控制系統設計用的線性化模型。常用的線性化方程表示如下:

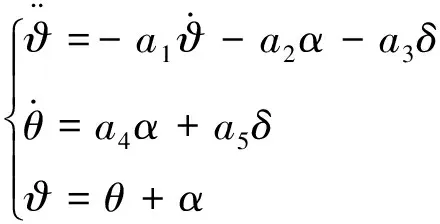
(1)

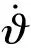
由此,可得如下傳遞函數:

(2)

(3)

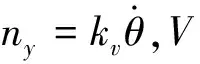
2 三回路過載駕駛儀結構

常用的偽攻角反饋三回路過載駕駛儀結構[9]如圖1所示,經典三回路過載駕駛儀結構[9]如圖2所示。圖1中:KAC,Kα和Kg為偽攻角反饋結構中的反饋系數;KDC,KA,ωi和KR為經典三回路結構中的反饋系數。在偽攻角反饋結構中,通常取A4=a4-a2a5/a3。圖2中:c表示加速度計在彈上的安裝位置,正的c表示安裝在導彈質心之前。

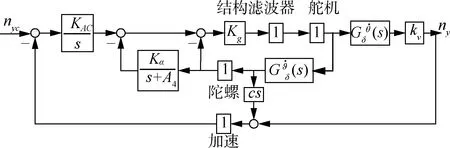
圖1 偽攻角反饋三回路過載駕駛儀結構圖

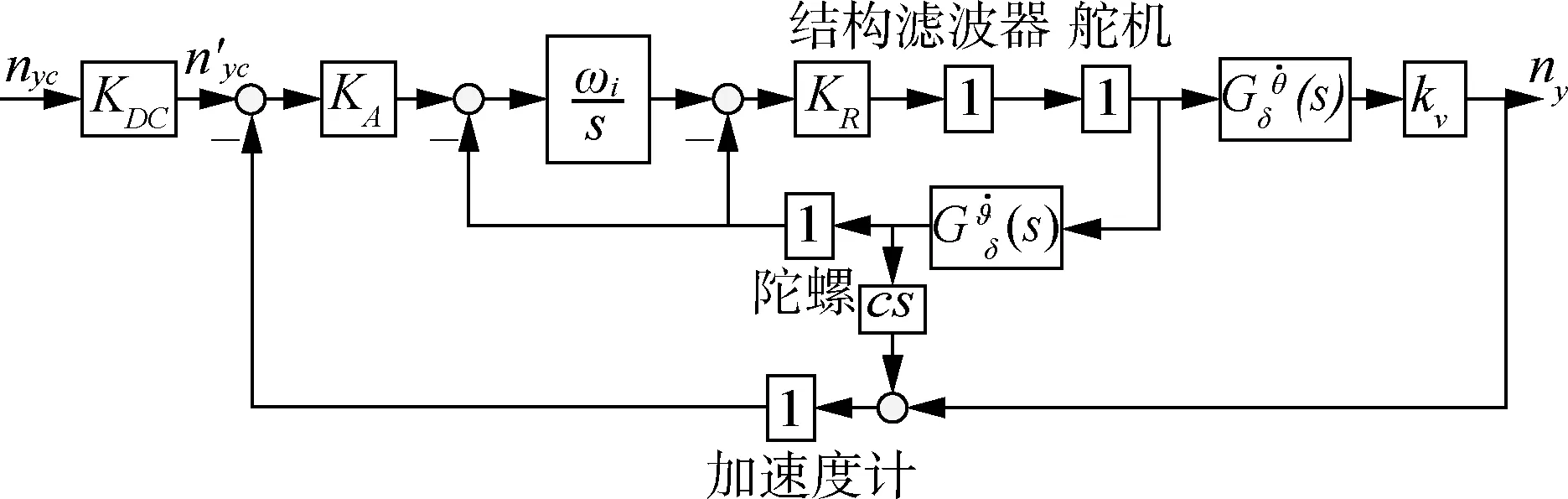
圖2 經典三回路過載駕駛儀結構圖

彈體氣動參數的不確定性是整個控制系統中最嚴重的環節,通常分析舵機斷開處的開環傳遞函數[10]。當忽略圖中舵機、速率陀螺、加速度計及結構濾波器的高階動態,對于偽攻角反饋結構,可得如下形式的開環傳遞函數(不考慮c):

(4)

式中:

(5)

同理,對于經典三回路結構,可得如下形式的開環傳遞函數(不考慮c):

(6)

式中:

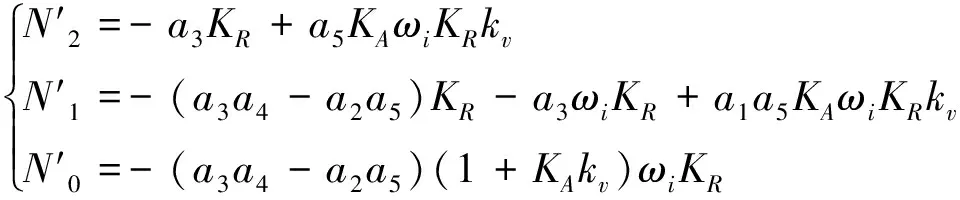
(7)

對比兩種結構形式的開環傳遞函數式(4)和(6),具有相同的形式。

定義:A1=a1+a4,A2=a2+a1a4;對于偽攻角反饋,可以求解從指令到過載的閉環傳遞函數:

(8)

顯然,其閉環傳遞函數穩定增益恒為1,說明偽攻角反饋結構對過載指令是一階無靜差系統[9]。

同理,對于經典三回路,可以求解從指令到過載的閉環傳遞函數:

(9)

在圖2結構中,設置前置補償系數[11]KDC能保證指令到過載的穩態傳遞系數為1。這是解決經典三回路對指令有靜差系統的補償措施。

3 三回路過載駕駛儀閉環特征方程與開環傳遞函數

對比式(8)和(9)可知,偽攻角反饋結構與經典三回路結構具有相同結構的閉環傳遞函數。當兩個結構中閉環傳遞函數相同時,式(5)和(7)應滿足:N2=N2′、N1=N1′、N0=N0′。

假設閉環傳遞函數的的特征方程為:

(10)

對于偽攻角反饋結構:

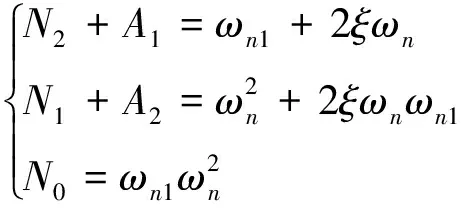
(11)

對于經典三回路結構可以推導,其結構形式完全相同,只是將式(11)中的Ni換為Ni′,i=0,1,2。

對于偽攻角反饋結構,利用閉環特征方程的參數,確定其控制回路增益,KAC,Kα和Kg如式(12)。

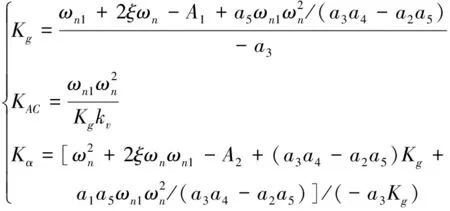
(12)

同理,對于經典三回路結構,其控制回路增益,KA,ωi和KR滿足如下關系:

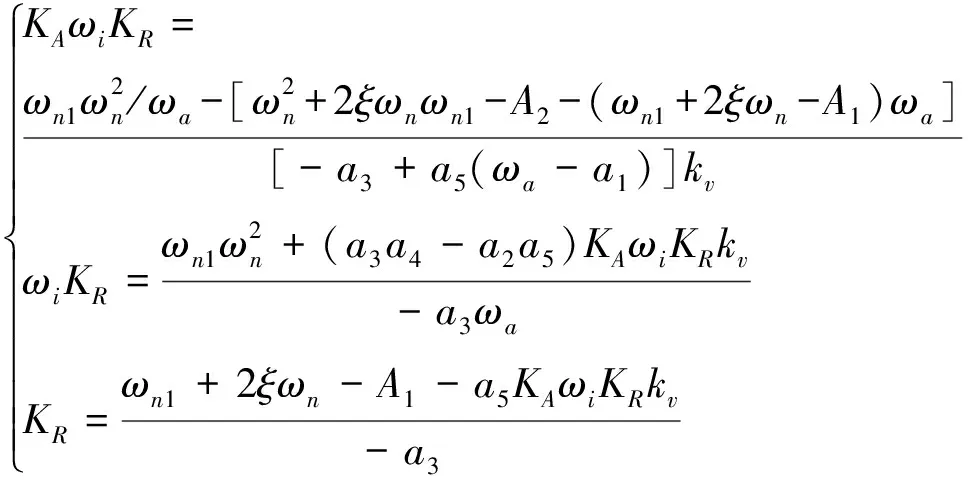
(13)

式中:ωa=a4-a2a5/a3=A4。

為方便后續描述,采用統一的表達形式描述系統開環傳遞函數為:

(14)

式中:

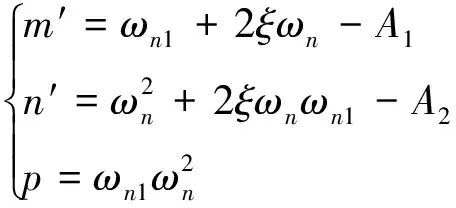
(15)

定義:

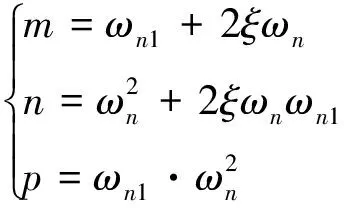
(16)

則:

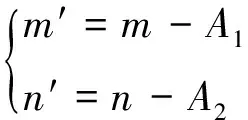
(17)

4 三回路過載駕駛儀參數設計

4.1 幅頻-相頻特性分析

根據系統開環傳遞函數HG(s),令s=jω,可得其幅頻、相頻特性:

(18)

定義復數:A(ω)和B(ω)如下:

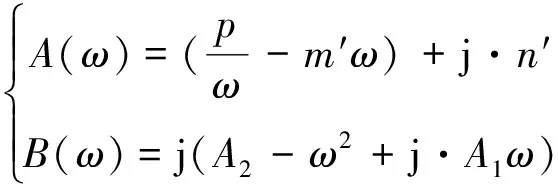
(19)

則復數A(ω)、B(ω)的幅值和相位分別為:

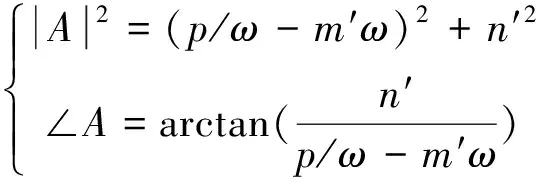
(20)

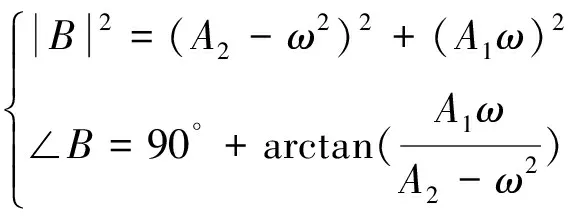
(21)

考慮慣性測量器件、舵機和結構濾波器等高頻部件對系統特性的影響,定義等效執行機構模型:

GACT(ω)=Γ(ω)∠φ

(22)

式中:Γ(ω)和∠φ分別為等效執行機構幅頻特性和相頻特性。

則系統開環幅頻-相頻特性表示為:

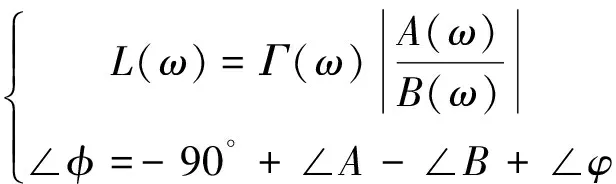
(23)

式中:L(ω)為系統開環幅頻特性,∠φ為系統開環相頻特性。

令系統開環幅值穿越頻率為ω=ωCR,則有:

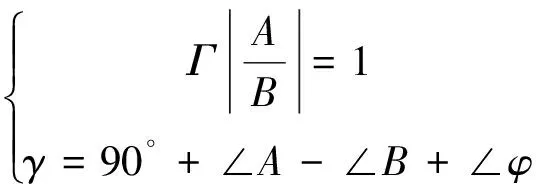
(24)

式中:γ為相位裕度。因此有如下關系式:

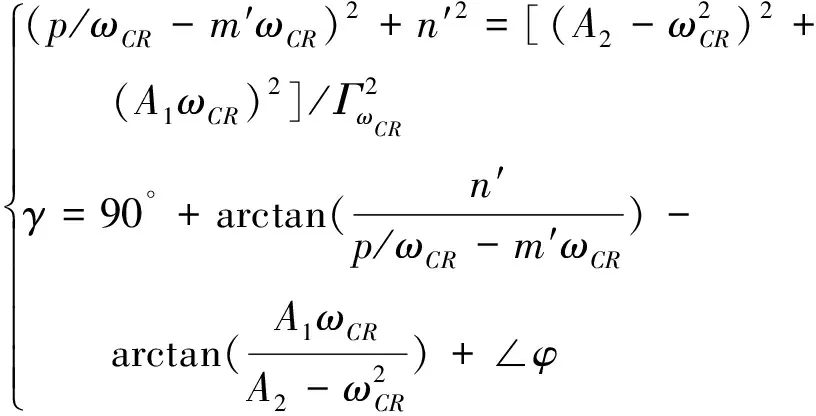
(25)

式中:ΓωCR為等效執行機構在幅值穿越頻率ωCR處的幅值。

令系統開環相位穿越頻率為ω=ωG,則有

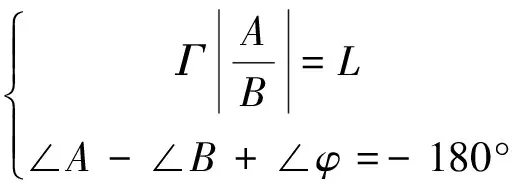
(26)

式中:L為幅值裕度。因此有如下關系式:

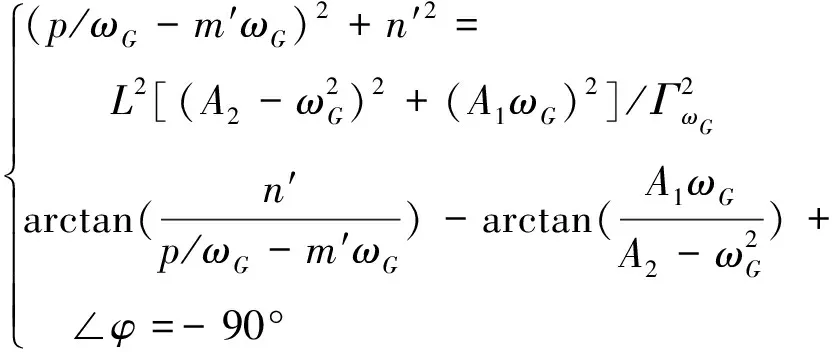
(27)

式中:ΓωG為等效執行機構在幅值穿越頻率ωCR處的幅值。

4.2 開環截止頻率的約束條件

定義:

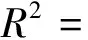
對于式(27)有:

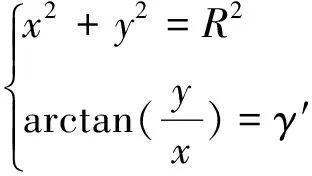
(28)

于是有:

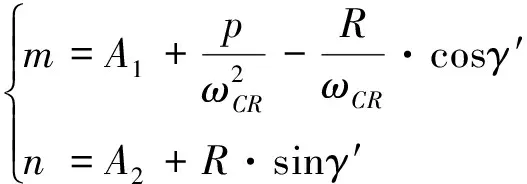
(29)

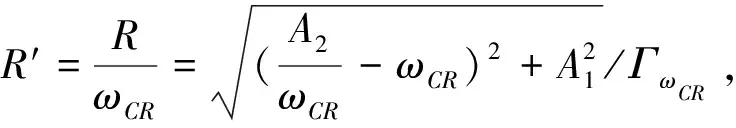
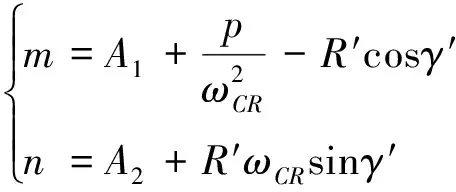
(30)

一般來說,工程設計中通常將ωCR作為系統帶寬指標。系統開環截止頻率的選擇主要受系統舵機帶寬、速率陀螺、加速度計及結構濾波器高階動態環節性能的制約。為保證系統穩定性,且高頻部件不對系統響應造成較大影響,工程上一般將自動駕駛儀開環截止頻率ωCR取為高頻部件等效帶寬ωACT的1/3～1/5[6],保證高頻部件在ωCR處引起的相移不超過30°。

4.3 最大舵偏角的約束條件

根據第3節分析可知,重新書寫偽攻角反饋結構的閉環傳遞函數:

(31)

由此可得,從指令到舵偏角及舵偏角速度的傳遞函數:

(32)

(33)

根據文獻[12-13],閉環系統響應的最大舵偏角速度在初始時刻產生,同時,注意到式(5),N0=-(a3a4-a2a5)KACKgkv,則有:

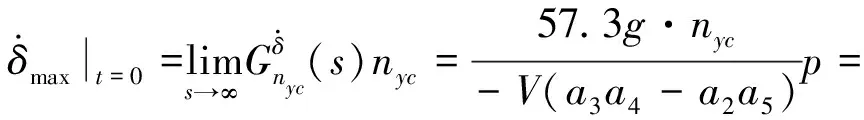
(34)

式中:δPH和αPH分別是指令為nyc時對應的平衡舵偏角和平衡攻角。

因此,考慮最大舵偏角速度約束,則有:

(35)

4.4 最小化閉環系統等效時間常數參數設計

根據式(16)和(30),可得如下關系:

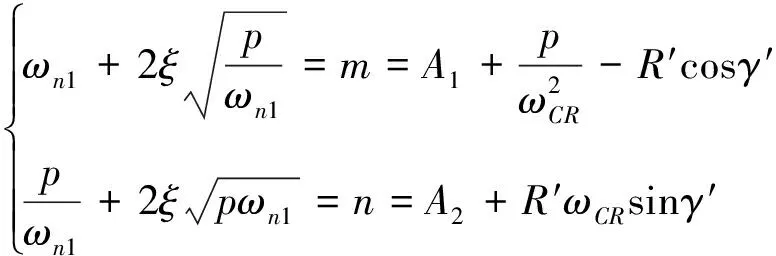
(36)

閉環系統等效時間常數為:

(37)

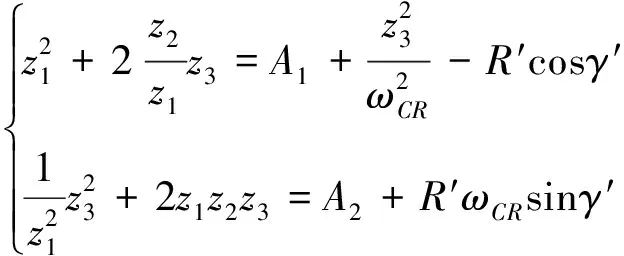
(38)

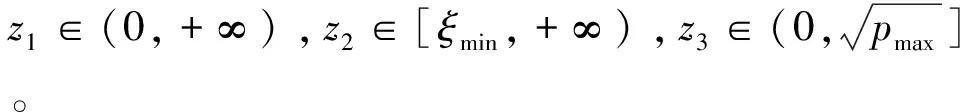
待優化目標函數為閉環系統等效時間常數:

(39)

綜上所述,設計過程可以概述為:

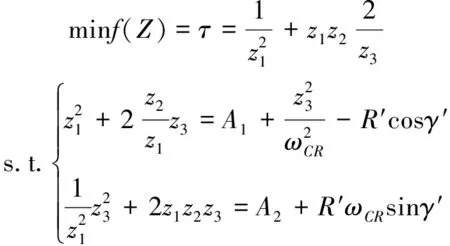
(40)

式中:

A1=a1+a4,A2=a2+a1a4,

求解式(40)的最優解:Zopt=[z1·opt,z2·opt,z3·opt],則有:

(41)

當不指定相位裕度γ的設計值,而僅指定其范圍γ∈[γmin,+∞)時,令z4=γ則設計過程表述為:

(42)

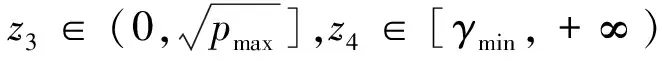
作此改進的目的是:當指定ωCR及γ,采用式(40)設計時,可能存在ωCR與γ不相容的情況。比如,對于靜穩定導彈,若ωCR設定的不是很大,但γ設定的又比較小,在此情況下,則會導致式(40)無解。當ωCR與γ相容時,式(42)的最優解滿足式(40)。即,使用式(42)按γ≥γmin尋優與使用式(40)指定γ=γmin尋優,結果一致;此時,對于式(42),按γ≥γmin尋優結果即是:γopt=γmin。

最后,使用系統幅值裕度對設計結果進行檢驗。

5 算例

表1 彈體氣動數據

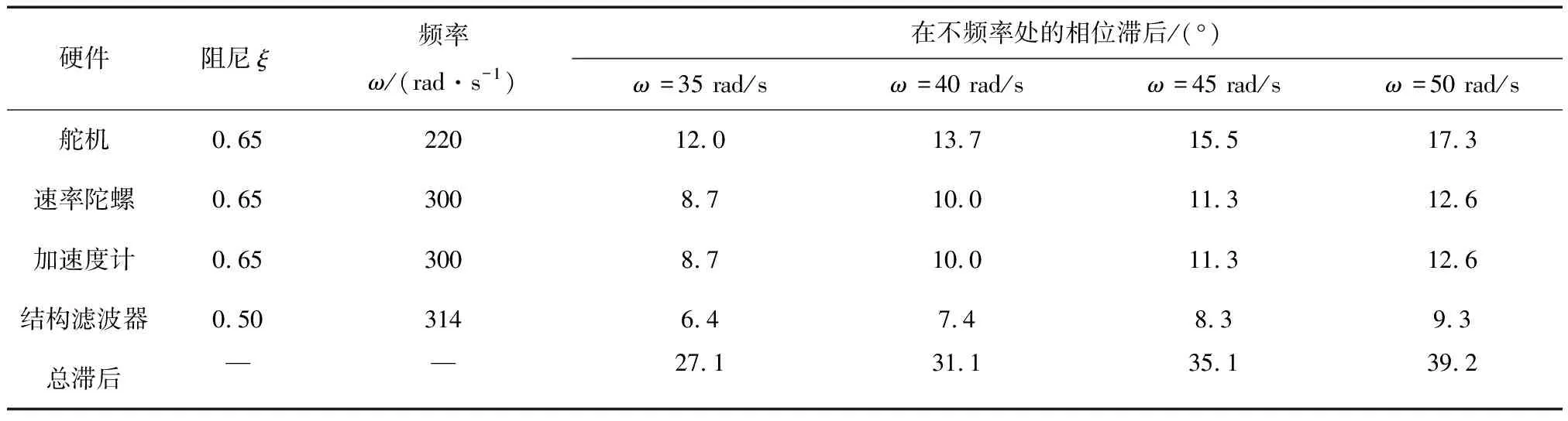
表2 硬件參數

對于上述硬件參數可以確定其等效執行機構的時間常數為[12]:

(43)

因此,可以取開環截止頻率ωCR=(1/3～1/5)ωACT=18～30 rad/s。采用本文提出的方法,對上述數據描述的系統進行設計,取定截止頻率ωCR分別為:40、45、50和55 (rad/s)及25、30、35和40 (rad/s);相位裕度γ=45°;阻尼比ξ≥0.6。對系統進行優化設計結果見表3所示。過載單位階躍響應曲線、過載單位階躍響應的舵偏角速度見圖3～6所示。

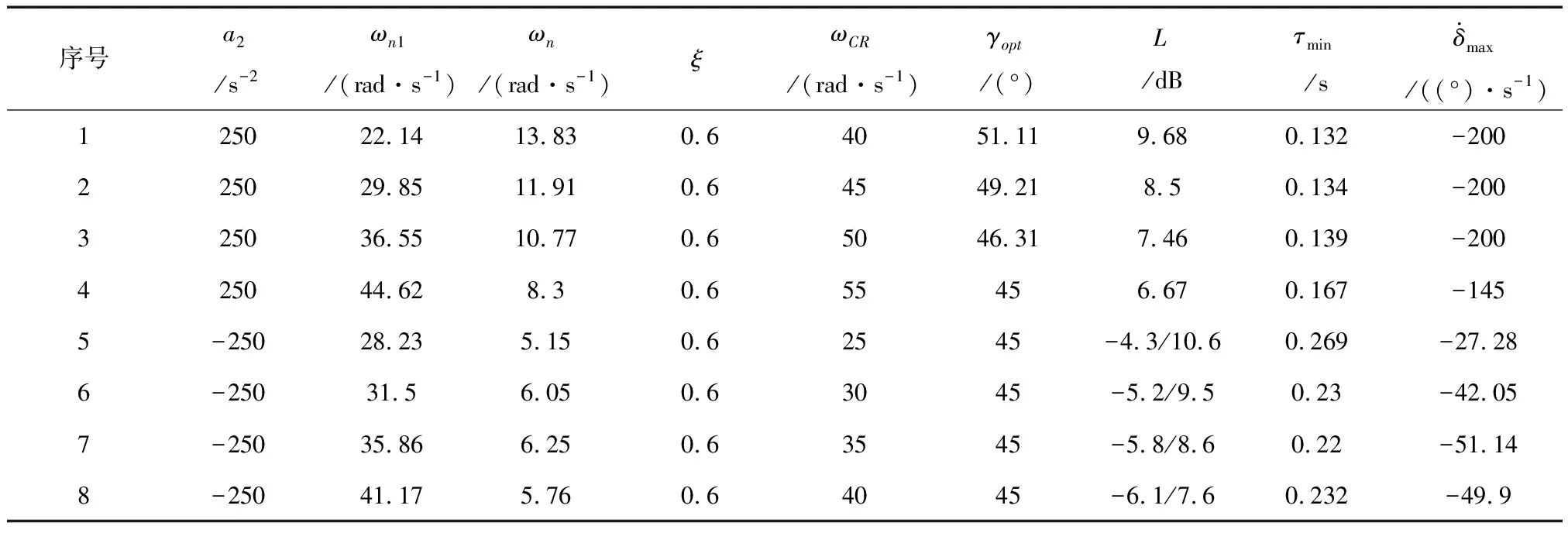
表3 設計結果

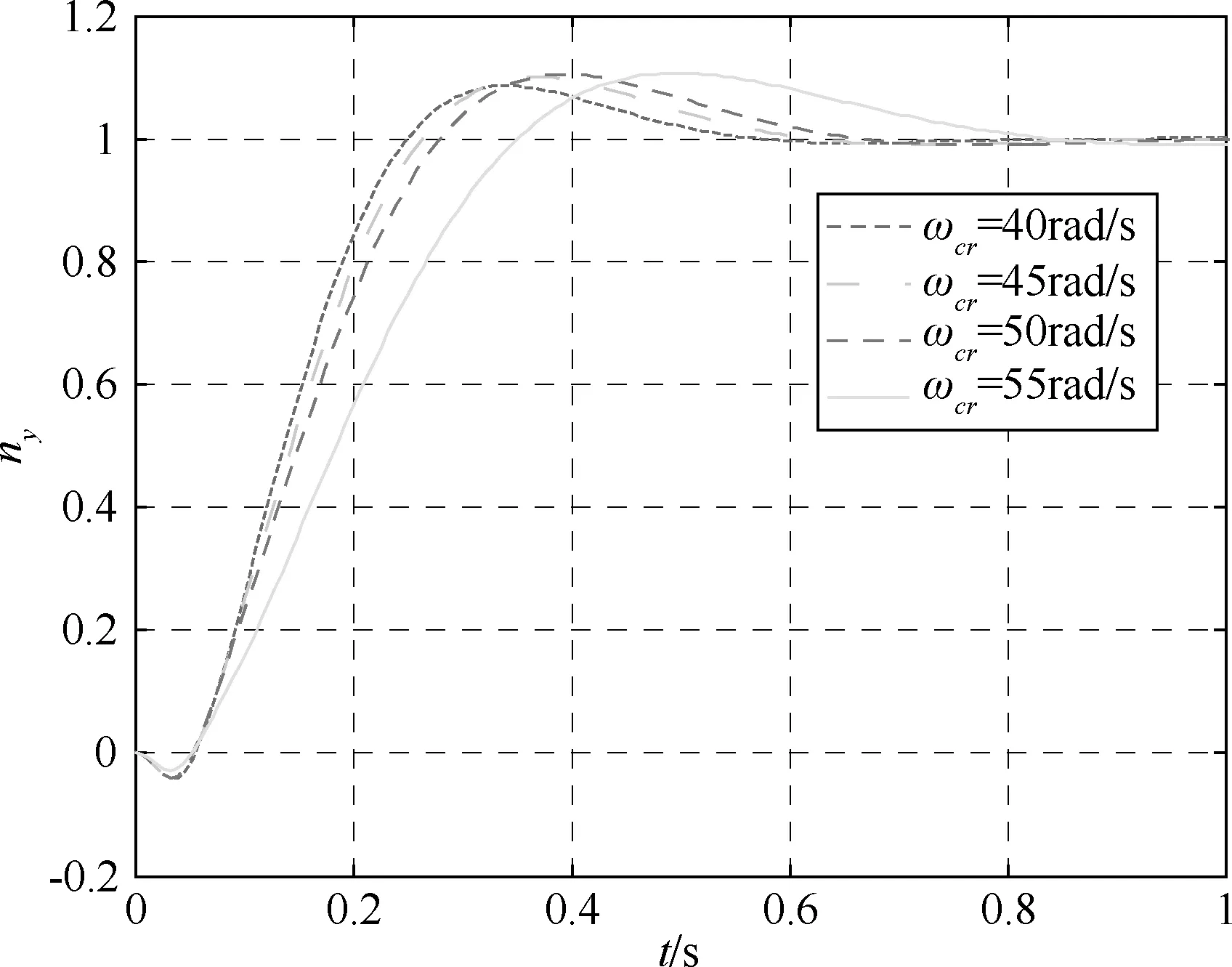
圖3 過載單位階躍響應(a2=250)

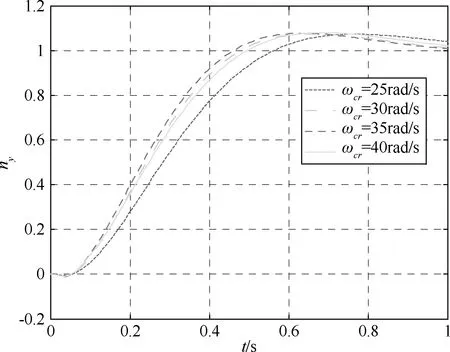
圖5 過載單位階躍響應(a2=-250)

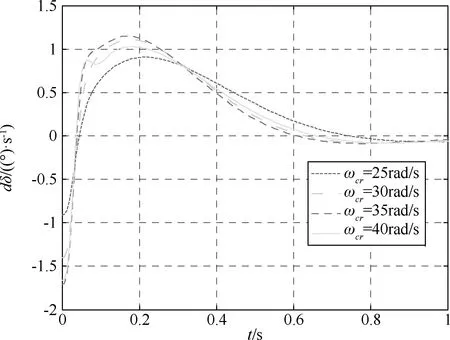
圖6 過載單位階躍響應下的舵偏角速度(a2=-250)

從表中序號1～3為“設置不匹配”的狀態,按照γ≥γmin尋優,其余狀態均按照指定的截止頻率與相位裕度設計。序號5～7中,對于靜不穩定狀態,低頻幅值裕度不滿足大于6 dB要求,當截止頻率提高到40 rad/s時,低頻幅值裕度滿足6 dB要求;但隨著截止頻率的提高,其高頻幅值裕度逐漸減低,因此,對于靜不穩定導彈,截止頻率存在一個最優值,即在指定的相位裕度條件下,綜合低頻幅值裕度與高頻幅值裕度。

6 結束語

通過對兩種常用的三回路過載駕駛儀的分析,給出了統一的閉環傳遞函數和開環傳遞函數,由此得出當兩種回路結構具有相同閉環極點時,兩回路結構具有相同的開環傳遞函數,因此,證明了在數學意義上兩種結構的等價性;同時,給出了兩種結構下由閉環極點確定控制回路增益的表達式;其次,通過分析開環傳遞函數得到開環截止頻率與相位裕度的關系式,并通過系統高頻部件對開環截止頻率進行約束,分析了閉環系統響應過程的最大角速度約束條件;最后,提出以最小化閉環系統時間常數為目標函數,通過求解帶約束條件的系統最優解,實現系統開環截止頻率、相位裕度的精確設計,并通過算例檢驗本文提出的設計方法的有效性。