動力擾動下充填體內預留巷道穩定性分析

羅福龍

摘要：巷道的穩定性是礦山安全高效生產的保障，在動力作用下實現充填體內預留巷道的穩定性預測，是指導工程實踐的關鍵。為了研究不同擾動下充填體內預留巷道的動力響應規律，以某礦山工程為研究對象，采用3DEC數值模擬技術，建立了巷道動力穩定性分析的三維數值模型，并進行了數值模擬分析。研究結果表明：對于馬蹄形巷道，同一水平的動力擾動對側幫的影響較大。隨著動力擾動距離的增大，巷道周圍質點振動的差異性越來越小。采用鋼絲繩+鋼筋網的預留巷道開采方式，能夠合理有效地對巷道外爆破動力擾動進行很大程度上的削弱，這對于巷道穩定性的保持是非常有利的。

關鍵詞：充填體；動力擾動；巷道穩定性；動力響應；數值分析；支護

中圖分類號：TD853.34? ? ? ? ? 文章編號：1001-1277（2023）06-0004-07

文獻標志碼：Adoi：10.11792/hj20230602

引 言

由于長期開采，淺層礦產資源日益減少。深部礦山“三高一擾動”的特殊環境使得深部開采機制和淺層開采機制之間存在很大差異。特別是在高地應力下，強烈的動力擾動會改變巖石的穩定性，使其表現出非常特殊的力學行為，甚至會導致巖爆、突水、采空區失穩和其他威脅采礦生產安全的災難性事故［1-5］。

國內外許多專家對巷道穩定性進行了深入研究：何滿潮等［6］通過理論研究、室內和現場試驗，證明各種動力擾動，包括地震、爆破、開采和掘進擾動對巷道圍巖的穩定性有重大影響。高富強等［7］創建了深部巷道二維動力模型，并使用有限元分析軟件分析強烈擾動下巷道圍巖的應力、位移和塑性場的變化。左宇軍等［8］使用RFPA軟件模擬了在動態應力條件下的深部巷道圍巖，分析了動態力學響應，并獲得了地應力狀態強度與圍巖失穩規律。李夕兵等［9］利用軟件對沙壩礦高應力巷道動力擾動進行了分析，探討了高應力巷道對動力擾動的力學響應規律。溫穎遠等［10］模擬了不同硬度煤層巷道圍巖在地震波影響下的反應，并分析了軟巖和硬巖煤層中巷道在動力擾動下的穩定性變化規律。胡毅夫等［11］以一大型深部巷道為例，對動力擾動下巷道圍巖力學響應進行數值分析，討論了巷道失穩與原巖垂直、水平應力及動態擾動強度大小的關系，并進行了巷道支護優化方案設計。

目前，有許多數值模擬方法可用于分析和評估巖體中巷道的變形和穩定性。在某些情況下，有限元法、邊界元法和拉格朗日法可用于通過接觸單元模擬不連續性。然而，上述方法不能自動識別計算過程中產生的新中斷面，只能模擬小變形或轉動。對于地下開挖的大變形問題，離散單元法更適合。目前，Cundall提出的離散元方法和Lemos改進的離散元法是分析不連續塊體應力變化的常用工具［12-13］。離散元方法可以有效地分析不同應力和應變條件下塊體的力學行為，并容易地計算大變形和完整巖體的復雜本構行為。3DEC軟件的優點是創建離散單元，實體在3DEC軟件中可以離散為黏結塊體模型（Bonded Block Model，BBM）［14］。

本文利用3DEC軟件對動力擾動作用下充填體內預留巷道的動態響應規律進行數值模擬分析，揭示動力擾動下充填體內預留巷道的應力波傳播特征和能量分布特征及支護前后巷道的穩定性變化，為理論分析提供依據。

1 數值模型及力學參數

1.1 模型的建立

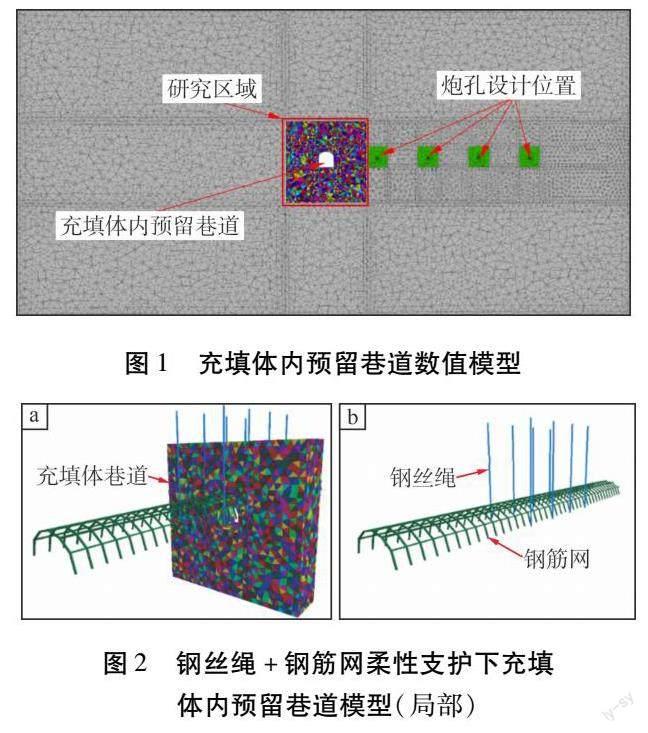
充填體尺寸為長×寬×高=40 m×40 m×60 m，充填體內預留巷道的尺寸為3 m×3 m的三心拱馬蹄形巷道。充填體研究區域被劃分為具有預定義尺寸的四面體，塊體大小與研究區域尺寸有關。

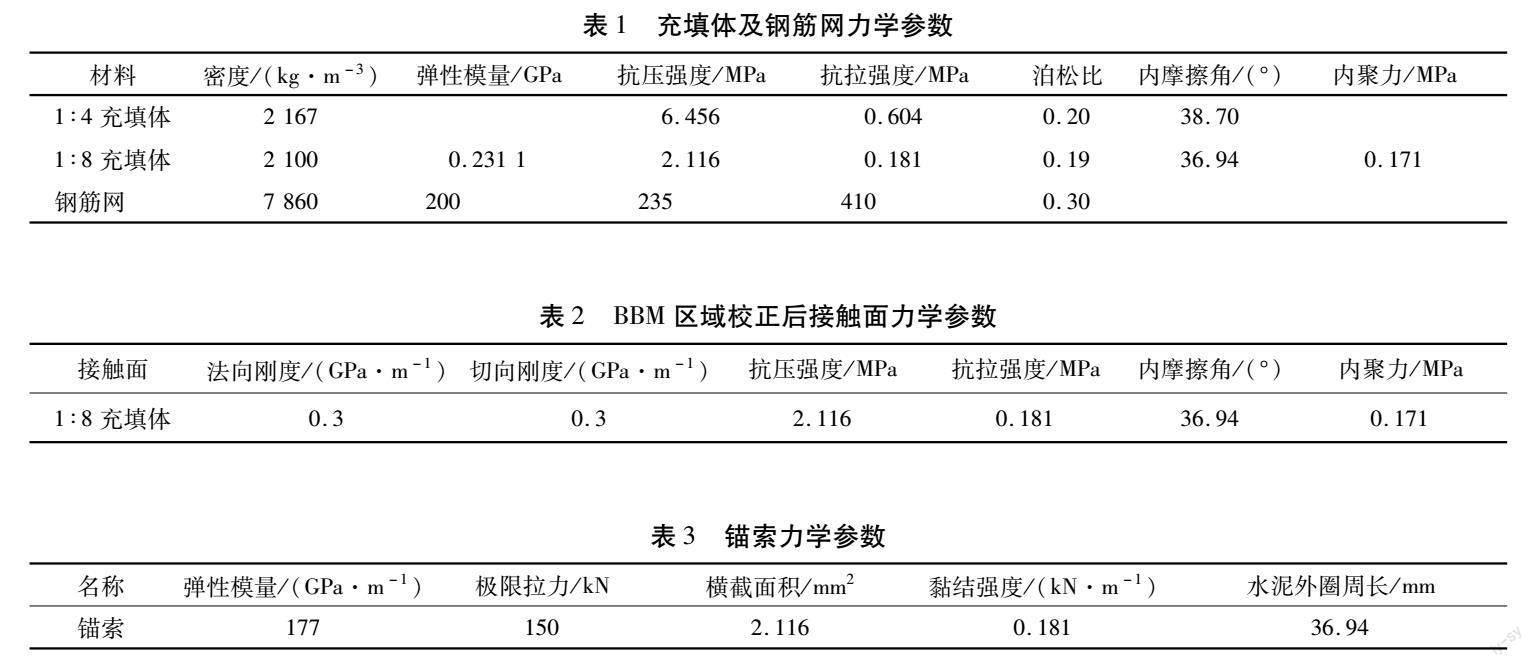
在充填體開挖現場，其支護材料采用鋼絲繩+鋼筋網的支護形式。在3DEC軟件中，由于缺少鋼筋網及鋼絲繩等支護單元，進而采用連續塊體單元賦予鋼鐵材料等力學參數實現鋼筋網的模擬，而鋼絲繩這一單元則采用錨索單元進行代替。

采用3DEC軟件建立的充填體內預留巷道數值模型如圖1所示。由于全模型采用BBM將極大地增加計算量，嚴重降低計算效率。因此，為了突出充填體損傷特征，僅在充填體預留巷道的重點研究區域，采用BBM模型進行充填體離散化處理，以獲得充填體受動載作用下的裂隙擴展規律，該研究區域長為5倍巷道半徑，寬為炮孔長度（3 m）。在模型的BBM區域，塊體遵守線性關系，接觸面采用摩爾-庫侖準則，模型其余部分采用連續體，其本構關系采用摩爾-庫侖準則。充填體預留巷道內鋼絲繩+鋼筋網形式的柔性支護如圖2所示。

1.2 充填體材料及支護材料力學性質

充填體材料分為灰砂比為1∶4及1∶8的充填體材料，力學參數如表1所示。從節約成本的角度考慮，本文采用灰砂比1∶8的充填體材料進行分析。

在BBM區域，由于該區域由塊體單元和接觸面單元構成，因此該區域的充填體塊體單元采用線彈性材料，塊體力學參數采用表1中灰砂比1∶8充填體材料力學參數，區域的破壞特征由接觸面之間的張拉、剪切進行表征。因此，接觸面采用彈塑性本構關系，經過參數校正，灰砂比1∶8的充填體接觸面力學參數如表2所示。本文數值模擬采用錨索代替鋼絲繩對鋼筋網進行拉伸處理，采用的錨索力學參數如表3所示。

2 柔性支護下（加網）巷道穩定性分析

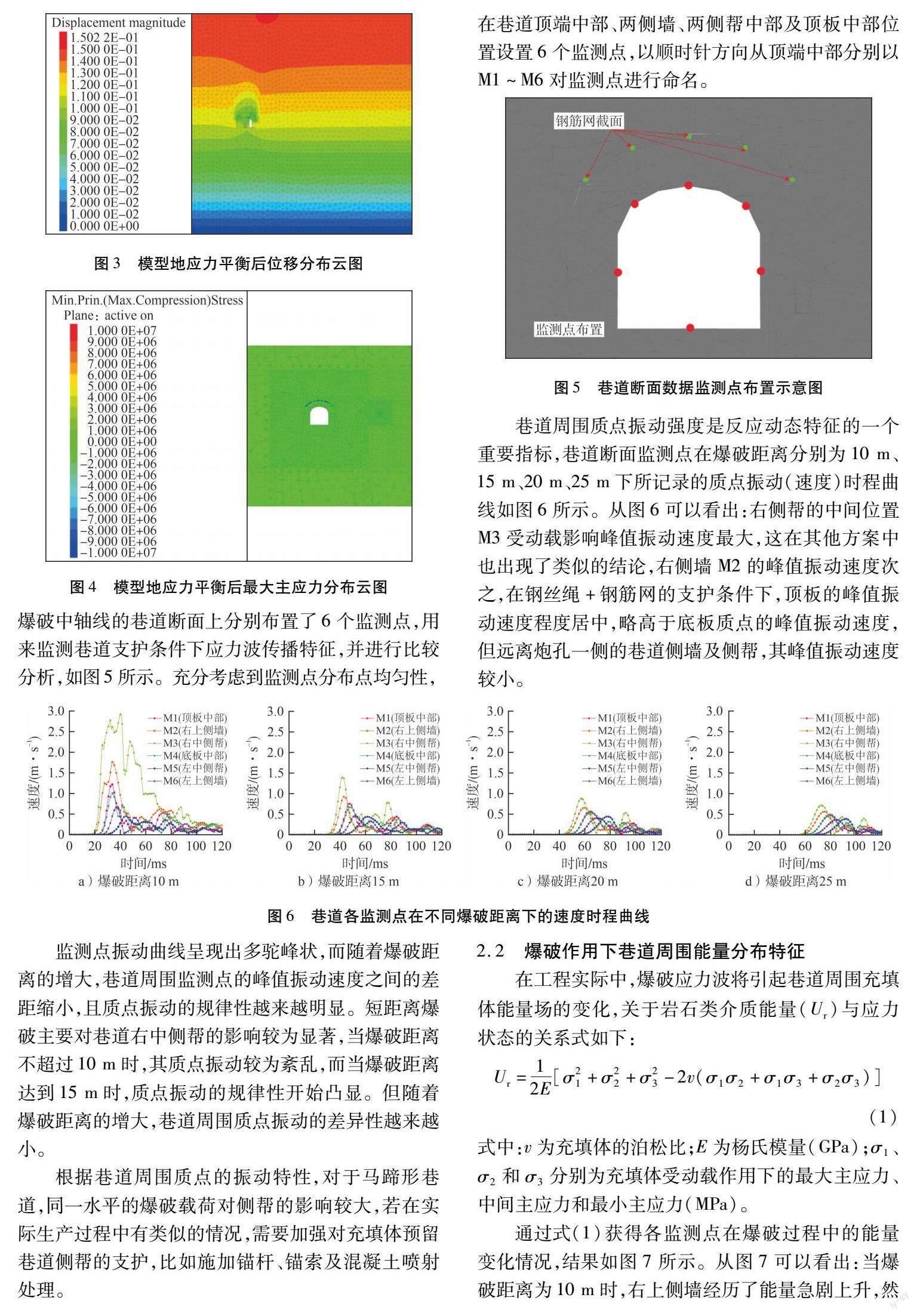
由于充填體存在著接頂不完全的情況，故數值模型僅考慮充填體自重應力的影響，模型僅施加自重應力的影響。在進行動力分析之前，首先進行模型應力平衡求解，如圖3所示。從圖3中可以看出，采用鋼絲繩+鋼筋網的支護方式，在采場充填完之后，有效減小了預留巷道周圍的位移場，說明在充填體自重應力作用下，預留巷道上方獲得了有效支撐。

最大主應力分布云圖（3DEC軟件中壓為負，拉為正，因此最小主應力實際上是最大主應力）如圖4所示。鋼筋網等支護結構成為了預留巷道上方主要承壓體，壓應力比較集中，而充填體內的應力分布較為均勻，從巷道周圍位移及應力分布上看，在自重應力的靜力作用下，鋼絲繩+鋼筋網的支護方式，對于保持預留巷道的穩定性起到了很好的作用。

2.1 爆破作用下巷道周圍應力波傳播特征

為了分析爆破應力波對巷道周圍的影響，在垂直爆破中軸線的巷道斷面上分別布置了6個監測點，用來監測巷道支護條件下應力波傳播特征，并進行比較分析，如圖5所示。充分考慮到監測點分布點均勻性，在巷道頂端中部、兩側墻、兩側幫中部及頂板中部位置設置6個監測點，以順時針方向從頂端中部分別以M1～M6對監測點進行命名。

巷道周圍質點振動強度是反應動態特征的一個重要指標，巷道斷面監測點在爆破距離分別為10 m、15 m、20 m、25 m下所記錄的質點振動（速度）時程曲線如圖6所示。從圖6可以看出：右側幫的中間位置M3受動載影響峰值振動速度最大，這在其他方案中也出現了類似的結論，右側墻M2的峰值振動速度次之，在鋼絲繩+鋼筋網的支護條件下，頂板的峰值振動速度程度居中，略高于底板質點的峰值振動速度，但遠離炮孔一側的巷道側墻及側幫，其峰值振動速度較小。

監測點振動曲線呈現出多駝峰狀，而隨著爆破距離的增大，巷道周圍監測點的峰值振動速度之間的差距縮小，且質點振動的規律性越來越明顯。短距離爆破主要對巷道右中側幫的影響較為顯著，當爆破距離不超過10 m時，其質點振動較為紊亂，而當爆破距離達到15 m時，質點振動的規律性開始凸顯。但隨著爆破距離的增大，巷道周圍質點振動的差異性越來越小。

根據巷道周圍質點的振動特性，對于馬蹄形巷道，同一水平的爆破載荷對側幫的影響較大，若在實際生產過程中有類似的情況，需要加強對充填體預留巷道側幫的支護，比如施加錨桿、錨索及混凝土噴射處理。

2.2 爆破作用下巷道周圍能量分布特征

通過式（1）獲得各監測點在爆破過程中的能量變化情況，結果如圖7所示。從圖7可以看出：當爆破距離為10 m時，右上側墻經歷了能量急劇上升，然后下降的過程，應變能變化的幅度最大，從破壞傾向性來看，右上側墻經歷了較為強烈的能量增加—減小的過程，該部位發生破壞的可能性較大；而其余部位應變能變化幅值在200 J/m3以內，其破壞的可能性均不及右上側墻部位。在爆破距離15 m時，右中側幫的峰值應變能超過了右上側墻，但差值并不大，兩個部位均經歷了較強的能量震蕩變化過程。當爆破距離為20 m和25 m時，巷道周圍部位應變能變化的趨勢及特征較為一致，僅在幅值上存在著一定的差異。

從應變能變化的角度上看，傳統采用質點振動的峰值速度來判斷地下結構發生破壞的標準較為單一，僅能作為一個參考價值，而工程實際中，建議以質點振動峰值速度+應變能的組合指標進行巖體破壞傾向性的判定。

2.3 不同爆破距離對巷道穩定性影響

根據工程經驗，爆破距離越大，對地下工程圍巖及構筑物的影響也就越小。隨著爆破距離的增加，應力波呈指數衰減，由于炮孔布置位置的特殊性，應力波主要對巷道右半邊的影響較大，對巷道周圍包括頂板中部、右上側墻、右中側幫及底板的分析較為有意義。因此，為了研究不同爆破距離對巷道穩定性影響，僅對頂板中部、右上側墻、右中側幫及底板中部的監測點進行分析。

頂板中部（M1）、右上側墻（M2）、右中側幫（M3）及底板中部（M4）在不同爆破距離下的速度時程曲線對比如圖8所示。在爆破距離大于10 m的情況下，各監測點的質點振動趨勢較為一致，而當爆破距離不超過10 m時，各部位的振動速度出現明顯的變化，具體表現在其峰值速度異常增大，且振動波形的跌落及回彈上升規律變得紊亂。這說明在充填體內裂隙的張拉、剪切等引起應力波的反射及折射，一方面導致了質點振動峰值速度的增加，另一方面導致了應力波傳播趨勢的無序性。

從圖8可以看出，爆破距離的增加對于巷道周圍質點振動的變化有較為明顯的削弱作用，可以斷定的是，爆破距離的增加，極大程度上減小了動力載荷的擾動，使巷道周圍的穩定性得到了保持。此外，對于充填體預留巷道來說，影響巷道穩定性的合理爆破范圍為10～15 m。

3 支護前后巷道穩定性對比分析

為了對充填體下預留巷道的穩定性進行分析，充填體中預留巷道采用塑料氣囊充氣-充填-塑料氣囊放氣的方法形成充填體內部的巷道。因此，在數值模型建立的過程中，其初始地應力的施加，以預留巷道附以空模型的形式建立，預留巷道上方不加支護時的位移分布云圖如圖9所示。與圖3進行對比可知，在自重應力作用下，巷道頂板的沉降量要明顯大于未支護條件下頂板的沉降量。

3.1 巷道周圍應力波傳播特征對比分析

不支護條件與支護條件下的質點振動速度時程曲線如圖10所示。由與支護條件下的巷道監測點振動速度時程曲線的對比分析可知：支護后，巷道右中側幫的質點振動峰值速度反而要高于未支護前的質點峰值速度，但在右上側墻和頂板中部等鋼絲繩+鋼筋網支護的影響范圍內，質點振動的峰值速度要明顯小于未支護前的質點振動峰值速度，這一點在左上側墻的質點振動速度時程曲線的對比中也可以看出。然而，在支護材料的影響范圍外，如在底板中部、左右兩中側幫的位置上，支護前的質點振動速度可能要小于支護后的質點振動速度。產生這一現象的主要原因是應力波在介質中傳播受到介質與節理、裂隙面的影響，若是在均勻介質中傳播，其質點振動速度不受鋼筋網、鋼絲繩等支護材料的影響;而在支護條件與未支護條件下產生質點振動差異的原因在于，當充填體受力不同時，若BBM中節理、裂隙產生張拉、剪切等破壞，使得新的自由面產生，由此增加了應力波的折射、反射面，使得應力波的傳播變得復雜。

但是，在巷道施加了支護材料后，在支護材料的影響范圍內，巷道周圍質點振動的速度要明顯小于未施加支護材料的質點振動速度。

3.2 巷道周圍能量變化對比分析

巷道支護前后應變能變化對比如圖11所示。從圖11可以看出：在各個監測點，未支護條件下，除了M2右上側墻應變能強度變化曲線的包絡線沒有完全覆蓋支護條件下應變能強度變化曲線的包絡線，其余各部位未支護條件下應變能強度包絡線均能將支護條件下應變能強度包絡線覆蓋，也就是說，支護條件下，巷道周圍的應變能變化幅度要遠比未支護條件下巷道周圍的應變能變化幅度小。

從應變能隨時間變化上看，對巷道頂板周圍采用鋼絲繩+鋼筋網的支護，能夠大幅度減小巷道周圍應變能的變化，減少動力擾動所帶來的能量釋放的影響，有效吸收了爆破沖擊波所帶來的破壞性能量。

總之，采用鋼絲繩+鋼筋網的預留巷道開采方式，能夠合理有效地削弱巷道外爆破動力擾動，這對于巷道穩定性的保持非常有利。

3.3 巷道周圍接觸面位移對比分析

支護前后預留巷道周圍裂隙法向位移量的對比分析如圖12所示。圖12-a）及圖12-b）中30 ms時紅色方框作為鋼絲繩+鋼筋網柔性支護的影響范圍區。從圖12可以看出：在應力波的傳播過程中，支護影響范圍區的裂隙法向位移量要明顯小于未支護條件下的裂隙法向位移量，且在未支護條件下，紅色方框內的裂隙一般呈現壓縮變形，對應于負的裂隙法向位移量。但是，隨著時間的推進，應力波的作用減弱，除了支護影響區域以外，巷道周圍其余部位的裂隙法向位移量未出現較為明顯的差異。

對應的支護前后預留巷道周圍裂隙切向位移量的對比分析如圖13所示。巷道周圍裂隙切向位移量的空間分布特點與法向位移量的空間分布特點較為一致。在應力波傳播的振中，即30 ms左右，巷道右側上墻周邊裂隙切向位移量的分布尤為明顯，在未支護條件下，巷道直接受到應力波的強烈沖擊影響。

4 結 論

1）為了更好地判斷地下結構是否發生破壞，以質點振動峰值速度+應變能的組合指標進行巖體破壞傾向性的判定。

2）對于馬蹄形巷道，同一水平的爆破載荷對側幫的影響較大。隨著爆破距離的增大，巷道周圍質點振動的差異性越來越小。爆破距離的增加，極大程度上減小了動力載荷的擾動，使巷道周圍的穩定性得到了保持。

3）對于充填體預留巷道來說，影響巷道穩定性的合理爆破范圍為10～15 m，以此可以指導工程實際。

4）在巷道施加了支護措施后，在支護措施的影響范圍內，巷道周圍質點振動的速度要明顯小于未施加支護材料的質點振動速度。采用鋼絲繩+鋼筋網的預留巷道開采方式，能夠合理有效地削弱

巷道外爆破動力擾動，這對于巷道穩定性的保持非常有利。

［參 考 文 獻］

［1］ 陳慶港.動力擾動下層狀碎屑巖巷道圍巖穩定性研究［D］.貴陽：貴州大學，2022.

［2］ 封雨捷.動力擾動下深部巷道圍巖破裂過程與動態失穩特征研究［D］.徐州：中國礦業大學，2022.

［3］ 牛虎明.開采擾動下非等強超前支護巷道圍巖響應［J］.煤礦機電，2021，42（6）：29-33.

［4］ 熊藤根，常聚才，史文豹，等.不同強度動載疊加下巷道圍巖力學特征數值模擬研究［J］.礦業研究與開發，2021，41（7）：118-122.

［5］ WU X Y，JIANG L S，XU X G，et al.Numerical analysis of deformation and failure characteristics of deep roadway surrounding rock under static-dynamic coupling stress［J］.Journal of Central South University，2021，28（2）：543-555.

［6］ 何滿潮，謝和平，彭蘇萍，等.深部開采巖體力學研究［J］.巖石力學與工程學報，2005，24（16）：2 803-2 813.

［7］ 高富強，高新峰，康紅普.動力擾動下深部巷道圍巖力學響應FLAC分析［J］.地下空間與工程學報，2009，5（4）：680-685.

［8］ 左宇軍，唐春安，朱萬成，等.深部巖巷在動力擾動下的破壞機理分析［J］.煤炭學報，2006，31（6）：742-746.

［9］ 李夕兵，廖九波，趙國彥，等.動力擾動下高應力巷道圍巖動態響應規律［J］.科技導報，2012，30（22）：48-54.

［10］ 溫穎遠，牟宗龍，易恩兵，等.動力擾動下不同硬度煤層巷道圍巖響應特征研究［J］.采礦與安全工程學報，2013，30（4）：555-559.

［11］ 胡毅夫，聶崢，鄧麗凡，等.動力擾動下深部巷道圍巖的力學響應及控制［J］.世界科技研究與發展，2016，38（2）：330-335.

［12］ SOULEY M，HOMAND F.Stability of jointed rock masses evaluated by UDEC with an extended Saeb-Amadei constitutive law［C］∥International journal of rock mechanics and mining sciences & geomechanics abstracts.Pergamon，1996，33（3）：233-244.

［13］ SOULEY M，HOMAND F，THORAVALA A.The effect of joint constitutive laws on the modelling of an underground excavation and comparison with in situ measurements［J］.International Journal of Rock Mechanics and Mining Sciences，1997，34（1）：97-115.

［14］ SUN X，ZHAO C，ZHANG Y，et al.Physical model test and numerical simulation on the failure mechanism of the roadway in layered soft rocks［J］.International Journal of Mining Science and Technology，2021，31（2）：291-302.

Abstract：The stability of tunnels is the guarantee for safe and efficient mining production，and predicting the stability of reserved tunnels inside fill bodies under dynamic forces is the key to guiding practical engineering.To study the dynamic response laws of reserved tunnels inside fill bodies under different disturbances，a certain mining engineering was taken as the research object，and a three-dimensional numerical model of tunnel dynamic stability analysis was established and numerically simulated using 3DEC numerical simulation technology.The research results show that for horseshoe-shaped tunnels，the impact of dynamic disturbances at the same level has a greater influence on the sidewall.As the distance of dynamic disturbances increases，the difference in particle vibration around the tunnel becomes smaller.The reserved tunnel mining method using? steel wire rope and steel mesh can effectively and reasonably weaken the dynamic disturbance from outside blasting to a great extent，which is very favorable for maintaining tunnel stability.

Keywords：fill body;dynamic disturbance;tunnel stability;dynamic response;numerical analysis;support