面向嵌入式系統的有效值快速算法

馬文博，羅 丹，蔣玉華，張億宗，廖志賢，黃國現

（1.廣西師范大學 電子與信息工程學院／集成電路學院，廣西 桂林 541004；2.桂林學院 理工學院，廣西 桂林 541006）

0 引言

有效值、峰值和平均值是廣泛應用于電機和電網的重要參數，對其采集和測量有著十分廣泛的應用場景，其中有效值可以直接反應有功功率大小，對其進行測量至關重要［1］。隨著越來越多的電氣設備接入電網，電壓、電流的波形可能因受到干擾而發生嚴重的畸變。在許多科學研究和應用場景，需要實時跟蹤這種畸變以消除其帶來的不利影響，因此需要一種穩定可靠的方法來準確測量非標準正弦波的有效值［2］。市面常見的數字或指針式萬用表的測量方法是依據平均值進行的，因此其輸出結果不是真有效值，依據此測量原理，它們只有在測量標準正弦波時結果是準確的［3］。在現有技術中，可精確測量有效值的方法有熱電偶法、RMS／DC運算法、數字采樣法等，其中熱電偶法、RMS／DC運算法的原理是將被測信號轉換為成比例的直流信號進行測量，采用該原理無法實時測量每一個周期的有效值；而數字采樣法通過高速ADC 對波形進行離散化采樣，并結合有效值的數學定義實現測量［4］。市面常見的真有效值測量芯片（如：AD637、AD736等）往往價格高昂、外圍電路復雜［7-10］，并不適合多路測量和大規模生產。

近年來國內外的學者都對有效值的應用和計算方法進行了大量探索。文獻［3］給出了交流電流有效值的物理意義和真有效值的概念。文獻［5］提出了一種電壓暫降檢測方法，該方法借助有效值對電壓暫降的幅值進行測算，文中指出了有效值算法存在實時性差的缺點，但對該缺點并未提出有效的解決辦法。文獻［6］基于真有效值檢測技術，利用土壤的介電特性，設計了一個高頻電容式土壤水分傳感器。文獻［7］通過AD637芯片設計了一種有效值轉換電路，但相比于單片機通過編程實現，其硬件相對復雜且成本更高。文獻［12］對比了LMC6482放大器代替二極管的精密整流電路和基于真有效值轉換器AD637的高精度轉換電路的測量精度和實現難度。結論為精密整流電路僅限于標準信號，而基于AD637的轉換電路的適用范圍更廣。文獻［4］對伺服調速系統的有效值測量方法進行了研究，并提出了數字離散同步采樣法進行信號的采樣，但由于采樣間隔和周期需要提前確定，對頻率不穩定的波形進行有效值測量時仍存在較大誤差。文獻［11］針對變頻器供電時交流電動機的輸入電壓和電流波形嚴重偏離正弦波的問題，提出一種電參量有效值測量的算法。文獻［13］指出 “有效值”是模塊化多電平換流器（MMC）設計過程中的一項重要指標，文章從理論角度推導了電流有效值的計算表達式，但并未解決實際場景下采樣和數據處理過程中的難點。文獻［14 -18］提出了基于Harr小波變換、準同步采樣、同步采樣等方法實現交流信號的數字測量和精度改進的方法。文獻［19］指出“有效值”在故障限流器（FCL）中快速判斷故障的應用，并給出微分法、迭代法、全周期采樣法等有效值測量方法［20-21］，但這些方法基于大量采樣值進行數學運算，不適用于需要實時響應的場景。

本文旨在通過嵌入式單片機（如STM32系列）的ADC轉換功能和DSP處理，設計一個高精度、高可靠性的有效值求解算法，其可適用于任何有峰波形，只需要少量外部參數即可穩定運行，其準確度高，通用性強、擴展性好，且不需要復雜的外圍電路，調試簡便，為后續各類有效值的應用提供便利。

1 系統結構及原理

為實現有效值的測量，系統需要對外部信號進行采樣。采樣電路需要擁有較高精度，以真實還原被測信號的情況。由于STM32單片機GPIO 只能接受0～3.3V 電壓信號，因此還需對輸入信號進行預處理和隔離，以適應不同的外部電壓輸入，防止輸入不符合上述要求時對系統造成不可逆的損傷。采樣模塊將經過調理的電壓信號輸入單片機，單片機通過ADC采樣、DMA 傳輸和適當的濾波程序，保證采樣速度和精度。為完整實現系統功能和人機交互，還需要電源電路、按鍵模塊、顯示模塊。本設計分別采用STM32F103C8T6和STM32F407ZGT6 兩款單片機完成設計和算法驗證，并進行對比分析。軟件部分主要完成采樣、濾波、峰值查找、有效值計算處理，并采用多種方式優化計算速度和準確性。

STM32F103C8T6是一款基于Cortex-M3內核的32位單片機，最高工作頻率可達72MHz，內置64KFlash存儲器和20KSRAM，它具有較強的性能，能夠滿足多種應用需求。其芯片價格相對低廉，非多路有效值計算場景下仍能保持較高實時性和可靠性［22］。

STM32F407ZGT6是一款卓越的多功能微控制器，可以滿足各種應用需求，它擁有高性能、低功耗的32 位ARM Cortex-M4F內核，有高達168 MHz的主頻，1 MB的Flash存儲器和192kB的SRAM，以及豐富的外設資源，如ADC、DAC、USB、SDIO、USART、高級定時器等，同時具有DSP單元和硬件單精度浮點運算單元（FPU），可以加快RMS、FFT 等數學運算的速度［23-24］。

本設計中主要用到主控制芯片中的ADC采樣和DSP內核，上述兩款單片機可完全滿足設計需求需求，STM32F407擁有更高主頻、更大ROM 和SRAM 和獨立的DSP處理單元、FPU 單元，可以更加快速地完成本算法，并留有一定擴展性。

2 硬件結構

系統硬件主要由STM32單片機最小系統、電源電路、信號輸入與調理電路以及部分人機交互模塊組成。

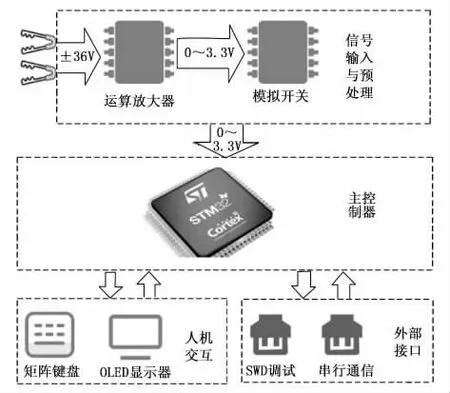
圖1 系統硬件整體框圖

圖2 信號輸入與調理電路圖

2.1 電源電路

系統電源可由外接6～20V 供電、7.2V 鋰電池、四節干電池等多種方案提供，可適用多種使用環境。

系統中運算放大器、模擬開關等器件均采用5V 供電，STM32單片機、OLED顯示屏采用3.3V 供電。本電路采用兩級LM1117LDO 芯片串聯組成，第一級將輸入電壓轉換為5V 輸出；第二級將5V 電壓轉換為3.3V，從而滿足系統各模塊的供電需求。LDO 芯片具有外圍電路簡單、低壓差下效率高、輸出紋波小等優點。

2.2 信號輸入與調理電路

為擴大測量信號輸入范圍，采用運放-模擬開關制作了多檔位量程切換器。本電路需要將外部的電壓輸入按比例放大或縮小，轉換為STM32單片機ADC 端口可以接受的0～3.3V 電壓，并通過模擬開關實現量程切換功能。

運放芯片采用LM324，該芯片具有4路獨立運放單元。其中，第一、二路構成跟隨器，根據電阻分壓公式：

第一和二路輸入電壓分別衰減為輸入的1／11、1／4。第三路構成同相比例放大器，放大倍數關系為：

其中：R32為平衡電阻，阻值計算方法為：R32＝R31／R30。第三路的放大倍數為11倍。

量程切換功能通過模擬開關實現，型號為CD4052。其A0、A1 連接至單片機GPIO 作為控制端，Y0B、Y1B、Y2B作為輸入端，ZB作為輸出端連接至單片機ADC 端口。單片機控制A0、A1以選通不同電壓等級輸入作為模擬開關的輸出。

表1 設計量程與電阻的關系

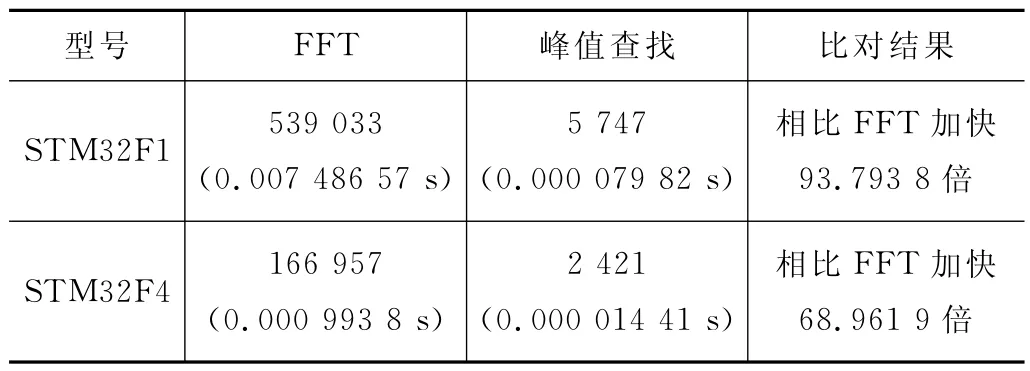
表2 時間復雜度比對

表3 準確度比對

2.3 單片機最小系統

單片機最小系統包含STM32主芯片、復位電路、SWD下載調試接口、晶振電路等。STM32F103C8T6與STM32F 407ZGT6外圍電路基本一致。

2.4 按鍵模塊

設計選用4＊4 矩陣鍵盤，從而實現人機交互輸入功能，并方便系統調試。該鍵盤引出4條行線，4條列線，分別連接至單片機GPIO 接口，用于行列掃描以判斷鍵值。

2.5 顯示模塊

系統通過OLED顯示屏向用戶展示系統運行時的各項參數和計算結果。

顯示模塊采用中景園電子1.91英寸sh1108OLED 顯示屏，其顯示分辨率為128×160。接口類型為spi。圖3為該模塊的電路圖。OLED有機發光二級管（organic light emitting diode）：即有機電激光顯示，指的是基于電流的作用，有機發光材料與有機半導體材料中的載流子符合及注入使得有機材料發光的技術［25］。

圖3 STM32F103C8T6最小系統的電路圖

3 軟件設計

有效值獲取算法通過STM32系列單片機進行驗證。軟件編寫過程分為初始化代碼生成和主程序邏輯代碼編寫。其中初始化代碼配置采用STM32CubeMX 工具生成HAL庫代碼。該工具通過圖形化界面直接生成STM32初始化代碼，相比于標準庫方便快捷，易于維護。主程序基于STM32cubeMX 生成的HAL庫初始化代碼，添加邏輯代碼完成。該程序采用C語言作為編程語言，基于Keil軟件進行編譯和調試。其主要目的是實現量程切換電路的控制、測量結果濾波、峰值點查找、有效值計算、按鍵狀態讀取、送入OLED屏幕顯示等。

3.1 初始化配置

1）矩陣鍵盤行線配置為輸出，列線配置為輸入。

2）將System core→RCC→High Speed Clock（HSE）配置為“CrystalCeramic Resonator”即將系統時鐘來源配置為外部時鐘；將Clock Configuration→Input frequency配置為8MHz，將Clock Configuration→HCLK（MHz）設置為168MHz（對于STM32F1系列應設置為72MHz）。

3）使能ADC1通道0用于輸入電壓信號采樣。ADC配置為獨立模式，禁用掃描，使能DMA 傳輸。為盡可能提高精度，ADC使用12bits模式以提供4096級精度，采樣時間設置為28cycles，以盡可能平衡采樣時間過長造成的采樣點數不足和采樣時間過短帶來精度不足的問題。觸發方式設置為由定時器2觸發。

4）定時器2配置。定時器預分頻值設置為168，計數值設置為200-1。當前系統時鐘配置為168 MHz，根據式（3）：

計算得到，當前定時頻率為5kHz。該數值可根據實際需要適當修改，對于較高頻率信號，該定時頻率應適當增加，但不能超過ADC單次采樣所需的時間，否則會造成采樣結果錯誤。對于較低頻率信號，該定時值應適當降低，以采樣到更多周期的信號（本算法至少保證采集1個完整周期波形即可正常運行）。

3.2 主程序設計

為保證有效值計算的準確性，其輸入必須為波形的一個或多個整周期。而如何準確快速找出一列未知波形的整周期是有效值計算過程中尤為關鍵的一步。常見處理方案有FFT（快速傅里葉變換法）、過零比較法等。FFT 由于算法中需要進行大量乘法和加法運算，在單片機等運算資源有限的場合下，可用性大大降低。過零比較法可以顯著降低單片機運算量，但該方法僅對波形過零時敏感，且需要硬件電路支持。對于較為復雜的波形，其仍存在明顯不足，如圖4所示，波形存在多個過零點，過零比較方法不適用。本文主要討論通過峰值查找算法，實現對一個（或多個）完整周期的提取。通過尋找一個周期中三個峰值，即可得到一個完整波形的區間。

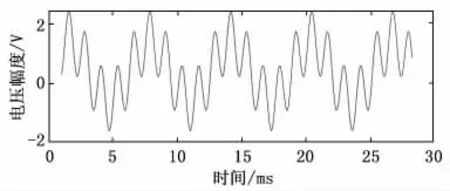
圖4 波形示例

圖5 峰值查找算法流程圖

圖6 峰值查找結果示例

該算法可用MATLAB 中findpeaks（）函數實現。該函數為盡可能保證通用性，進行了大量冗余判斷，在MATLABr2021b版本中，代碼量超1 130行。對于單片機系統，需要更加精簡的C 語言代碼實現，從而降低時間、空間復雜度。

算法分析：為確定峰值，實際上需要找到波形中一系列點x，滿足如下關系：

算法運行時，首先判斷是否滿足上述條件，將滿足該條件的點設置為峰值參考點。之后找出峰值參考點中的最大值，判斷每一個峰值參考點是否數值上相距最大值過遠（即大于某個人為指定的閾值）；判斷該參考點與上一參考點距離是否小于峰值間隔閾值（該閾值由人為指定，一般通過預先判斷輸入類型和頻率范圍，從而確定峰值最小間隔），二者符合其一則判定為次高峰，而忽略不做處理。否則將該參考點標記為峰值點，并繼續重復執行上述過程，直到遍歷結束。

上述算法執行結束后，將得到所有波形峰值點的數組下標。隨后取出波形中的三個峰值點，即可確定波形的一個周期。

完成完整周期查找后，即可進行均方根值計算。根據有效值定義式（5）：

式中，T為信號的周期。其離散化公式為：

式中，N為參與計算的采樣點數，Xi為采樣信號在第i次采樣時刻的瞬時值。

根據式（5）、（6）計算原理，當且僅當輸入為一個或多個完整周期時才能得到準確的結果。利用峰值查找的結果，即所有波形峰值點的數組下標，完整周期長度N可通過如下方法求得：

式中，Num為峰值點下標數組，n為起始點。在圖7的結果中，n＝1。

圖7 多sin疊加波形峰值查找結果

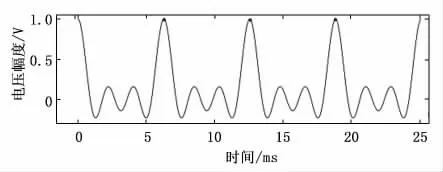
圖8 Dirichlet波形峰值查找結果

圖9 mstg函數波形峰值查找結果

隨后需要提取源數組中Num［n］至Num［n＋2］區段作為均方根值計算的輸入數組，具體可通過如下C 代碼實現：

代碼主要功能是將源波形數組中一個整周期Num［n］至Num［n＋2］區段各個數值轉存入新數組中，其中RMS＿In為均方根值計算的輸入數組，Src為源波形數組。

均方根值在嵌入式處理器中實際計算過程可通過兩種方案實現：

方案1：通過DSP庫內置函數：

參數1為均方根值計算的輸入數組RMS＿In，存放一個或多個整周期波形全部采樣點的數值；參數2為數組長度N；參數3為函數輸出變量指針。調用該函數后＊pResult所指內存空間將產生均方根值計算結果。

方案2：根據定義式（6）進行計算。

相比于方案2，方案1經過軟硬件優化，保持結果準確性的前提下運算速度更快。

4 實驗驗證與對比分析

4.1 試驗方案

本算法最終目標是實現應用于嵌入式處理器的任意有峰波形的有效值計算功能，驗證分為計算機模擬理論準確性驗證及嵌入式處理器運行驗證，分別設計不同實驗以全面驗證算法可靠性、準確性、時空復雜度等。

在時空復雜度測試中，將本文提出算法與快速傅里葉變換法（傳統算法）進行對比。快速傅里葉變換法（FFT）主要用于解決離散傅里葉變換（DFT）中計算量過大的問題，大幅降低了借助于計算機的傅里葉變換求解過程中的算法復雜度［26］。在STM32系列單片機中調用DSP 庫中的FFT 函數即可求得波形的頻譜，頻譜中除直流分量外第一個幅值明顯較高的點位即可認為整體波形的頻率點。根據式（8）：

可求得算法所需的頻率參數，式中，n為FFT 輸出數組下標，Fs為采樣頻率，采樣點數N＝2n，其中n需為4到12間的整數，f為FFT 數組下標對應波形的頻率。本文取n＝10，即N＝1 024，Fs取1 024，此時根據式（9）：

FFT 分辨率為1Hz。因此對于非整數頻率測量中采用FFT（傳統算法）會引入較大誤差。

4.2 算法可靠性驗證

波形峰值查找準確性是決定有效值輸出結果正確性的關鍵所在。通過本文編寫的C 語言代碼與調用MATLAB工具箱中findpeaks（）函數進行峰值查找、調用rms（）函數進行有效值計算結果進行對比。處理多組數據，觀察輸出結果。算法中均只保留3個連續峰值，其余峰值和次高峰做忽略處理。

測試數據1：多sin疊加波形

1）MATLAB程序測試：圈出的波形位置為查找的有效值所在位置。

輸出峰值數組下標：17，80，143

RMS值：1.230 5

2）C語言程序：

輸出數組下標：16，79，142

RMS值：1.230 466

測試數據2：Dirichlet（混疊正弦函數）波形

1）MATLAB程序測試：圈出的波形位置為查找的有效值所在位置。

輸出峰值數組下標：62，125，187

RMS值：0.372 0

2）C語言程序：

輸出數組下標：61，124，186

RMS值：0.372 003

測試數據3：mstg函數波形

1）MATLAB程序測試：圈出的波形位置為查找的有效值所在位置。

輸出數組下標：401，801，1201

RMS值：0.872 0

2）C語言程序：

輸出數組下標：400，800，1 200

RMS值：0.872 016

注：因MATLAB數組下標起始值為1，C 語言數組下標起始值為0，故C語言輸出下標值較MATLAB輸出下標值少1，指代數組中的相同數據。

測試結果：對于任意復雜度的有峰波形信號表現出極高準確性和穩定性，C語言程序與MATLAB程序輸出峰值點查找結果一致，RMS值計算結果一致。

4.3 時間復雜度比對

分別使用STM32F1系列單片機（基于Cortex-M3內核，無DSP處理單元，主頻72 MHz）、STM32F4 系列單片機（基于Cortex-M4內核，有DSP 處理單元，主頻168 MHz）兩款單片機，對一組相同數據進行FFT 運算（即傳統算法）求得波形頻率，進而根據采樣率換算找出整周期區間，求得均方根值、使用本文峰值查找算法求得波形一個整周期，進而求得均方根值，通過STM32仿真器觀察states（指令周期數），比對二者所需指令周期差異。

運行峰值查找算法所需時間較FFT 大幅縮減，尤其在主頻更低、成本更低、無FPU 和DSP 處理單元的STM32F1系列單片機中，通過峰值查找的均方根求解算法較傳統算法加速效果尤為明顯。

4.4 空間復雜度比對

傳統FFT 算法執行時，需要定義輸入數組（長度為輸入數據長度2倍）、輸出數組（長度與輸入數據長度相同），而本算法可直接利用源數組作為峰值查找算法的輸入，定義較小數組長度作為算法所找峰值點輸出，算法運行時無需開辟其他內存空間。在源數據長度較長時，使用峰值查找算法可顯著降低空間復雜度，不考慮FFT 運行過程中額外內存開銷的條件下，總內存空間節省量為源數組長度3倍以上，有效節省單片機片上內存資源。

4.5 準確性驗證

通過RIGOL DG4000系列任意波形發生器產生幅值不同的非標準波形信號，接入上述兩款單片機ADC 端口，單片機進行采樣和計算后，通過OLED 屏幕顯示有效值數據。通過與UNI-T UT71C型號萬用表的真有效值測量功能與單片機測量結果進行對比，分析測量誤差。

在20 次模擬實驗中，樣機測量結果與UNI-TUT71C型號萬用表測量結果整體相近，平均誤差為0.57%。算法對于不同種類的非標準周期波形均能有效識別峰值，并計算有效值。誤差多為隨機誤差，信號采樣電路、ADC 轉換和部分外部因素會引入測量誤差，整體誤差可控，符合實際應用要求。

5 結束語

本文提出的真有效值快速算法首先通過峰值查找確定波形中的一個周期，然后在一個（或多個）整周期中使用RMS計算函數計算波形的真有效值。相比于傳統的FFT 求頻率，進而得到周期的辦法，其計算效率有了顯著提高，為單片機片上多路RMS值實時計算提供了有效的解決方案。本方案無需任何用于獲取頻率、周期、RMS值的外圍電路參與，很大程度上降低了硬件成本，同時該算法無需滿足傳統有效值算法中 “采樣頻率須等于交流信號頻率的整數倍或有理分數倍”這一硬性條件，增強了算法適用范圍，可實時獲取任意非標準波形的有效值。經與標準儀表對比，本算法擁有較好的準確性和穩定性，可進一步推廣使用。