基于旋轉運動的試驗氣流場產生方法數值研究

黃亞飛，蔣興良，鄭華龍，馬列

(重慶大學 輸配電裝備及系統安全與新技術國家重點實驗室，重慶，400044)

氣流場試驗是空氣動力學研究的重要手段，是航空航天、能源、交通運輸、環境以及建筑等領域的重要技術[1-2]。空氣動力學來源于流體力學，伴隨著航空航天工業的發展而迅速發展，自20 世紀60 年代以來，隨著建筑、能源、運輸以及交通等工業的發展，空氣動力學朝著多目標多場景發展。目前，空氣動力學的主要研究手段包括理論分析、數值模擬以及氣流場試驗，三大研究手段在空氣動力學的發展中都發揮了重大作用[3-5]。尤其是以風洞試驗為代表的氣流場試驗，不僅為飛行器等設備提供可靠的設計依據，促進了航空航天工業的發展，而且有力地促進了空氣動力學的發展[6-8]。迄今為止，氣流場試驗仍是研究空氣動力學特性的重要手段。

現有的不同形式的風洞主要用于飛行器整體、機翼等設備的氣動特性的試驗研究[9-11]。首先，高精度風洞設備的設計與建設成本高昂，占地面積及運行功率極大。其次，對復雜大氣環境工況下的模擬試驗，如高速動車組牽引機車車頂高壓設備在大霧、沙塵環境下的高速運行，風力發電機葉片在高海拔、冰雪環境下的高速旋轉等，難以在傳統風洞中進行模擬試驗[12-13]。因此，亟需一種新的試驗氣流場產生方法，以較低成本實現設備在復雜環境高速氣流中運行性能的檢測，推動氣流場試驗技術的發展。

由于旋轉流場現場實驗以及測量手段匱乏，數值模擬仍是研究的主要手段[14-16]，而旋轉參考系方法和搭接網格方法在旋轉流場的數值求解中發揮了重要作用，被廣泛應用于泵類機械[17-18]、直升機旋翼[19-20]、風力發電機[21-22]、生物攪拌器[23]以及車輪制動盤[24]等研究。

因此，根據相對運動原理并參考風洞和傳統的旋轉臂設備，本文提出一種基于旋轉運動的試驗氣流場產生方法。該方法流速的產生方式與傳統風洞的不同，是在有限試驗空間中通過圓周驅動的方法將加速涵道結構加速至高速，在涵道試驗段內形成高速試驗氣流，以低成本的方式實現高速氣流及復雜大氣環境甚至高壓電場的綜合氣流場試驗條件。建立基于旋轉參考系以及滑移的數值求解模型對試驗空間內的三維旋轉流場進行模擬計算，評估試驗段內的流場分布特性，從流速和流場均勻性的角度驗證基于旋轉運動的試驗氣流場產生方法的可行性。

1 基于旋轉的均質氣流產生方法

圖1所示為基于旋轉運動的試驗氣流場產生方法的示意圖。試驗室內部形成密閉試驗空間，高速旋轉驅動系統放置在試驗室內。試驗室采用密封絕熱設計，以滿足模擬低溫低壓試驗環境的要求，可以模擬各類復雜大氣環境。

圖1 基于旋轉運動的試驗氣流場產生方法示意圖Fig.1 Schematic diagram of experimental flow field generation method based on rotating motion

高速旋轉驅動系統主要由自平衡導軌與滑臺系統、高速驅動與傳動系統組成。自平衡導軌與滑臺系統是高速運動平臺的核心，主要起支承均流加速涵道高速運轉的作用。導軌系統由上下2個大尺寸圓形導軌和安裝在其上的2個滑臺組成，導軌與滑臺系統配合限定旋轉部件只沿導軌做高速圓周運動。為了保證系統高速旋轉時的穩定性，流場控制涵道對稱側安裝有補償質量自動分布型自動平衡裝置，以抵消旋轉系統本身的不平衡。均流加速涵道由收縮段、試驗段以及擴散段組成，通過滑臺固定在導軌之間，通過旋轉主軸和旋轉支撐桿的帶動在導軌上做高速圓周運動。

理論上，基于旋轉運動的試驗氣流場產生方法可以在涵道試驗段內產生高速氣流，并且可以實現高速氣流與復雜大氣環境的綜合氣流場試驗條件。本文將從試驗段內流速和流場品質的角度對其流場分布進行深入分析。

2 有限空間三維旋轉流場數值計算模型

為了方便對比，將有限空間內的三維旋轉流動當作可壓縮湍流流動處理。本文采用多參考系計算模型結合滑移網格方法對其進行求解。將流體域劃分為外場和內場2部分。內場計算域模型采用旋轉參考系，將時變流場求解轉變為非時變流場進行求解；而外場計算域模型采用常規靜止參考系，通過插值的方法進行內外場計算域數據傳遞。

2.1 多區域計算域建模

流場計算域如圖2所示，其中，內場計算域主要為旋轉的加速涵道，外場計算域主要為密閉空間的靜止壁面，r為涵道的旋轉半徑，R1為內場計算域外徑，R2為外場計算域外徑，H1為內場計算域高度，H2為外場計算域高度，D1為涵道收縮段入口半徑，D2為涵道試驗段半徑，D3為涵道擴散段出口半徑，L1為涵道收縮段長度，L2為涵道試驗段長度，L3為涵道擴散段長度。將外場計算域分為3 個部分，分別為上下的圓柱體以及周圍的圓環體。計算域以及涵道的具體參數如表1所示。

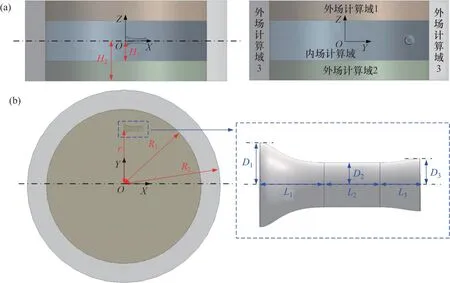
圖2 流場計算域Fig. 2 Flow field computing domain

表1 流場計算域參數Table 1 Parameters of flow field computing domain

2.2 局部控制混合網格劃分策略

通過分區劃分、混合處理、局部控制等方法形成多區域混合網格。其中，外場計算域分為3個部分后，采用掃略方法生成六面體結構化網格；內場網格由于包含涵道結構，是不規則的形狀，則生成以四面體為主的非結構化網格。

為了確保計算精度，采取局部控制的方法對涵道周圍網格進行局部加密處理，涵道周圍球形區域內的網格尺寸約束為整體網格控制尺寸的40%。其中，在試驗段最主要的流動觀察區域，將試驗段內的網格尺寸約束為整體網格控制尺寸的15%。根據本文使用的k-ε模型以及增強型壁面函數的要求，根據壁面距離(量綱一的量)y+=30 確定近壁區的邊界層網格的首層高度；邊界層的長寬(即涵道結構的面網格尺寸)則按照邊界層網格首層高度的100 倍確定，然后按照擴散比1.2 生成5 層邊界層網格。數值計算網格如圖3所示。

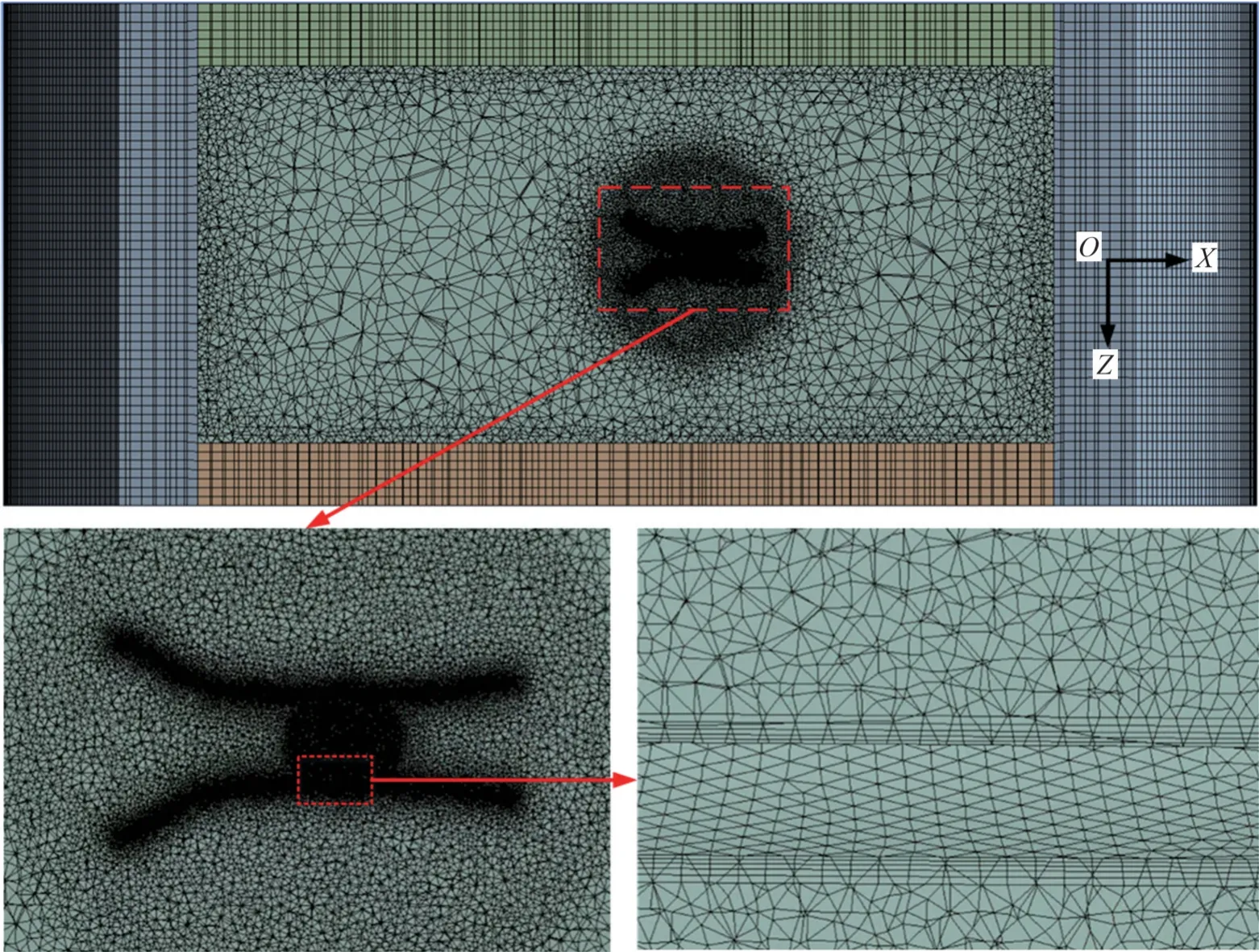
圖3 數值計算網格Fig. 3 Numerical mesh

為了確保計算的準確性，分別采用RNG 模型和Realizable 模型對數值網格的獨立性進行研究，得到涵道內平均流速隨整體網格控制尺寸的變化情況如圖4所示。從圖4可以看出：在當整體網格控制尺寸從0.20 mm降到0.14 mm后，網格控制尺寸對涵道內流場分布的影響可以忽略。后續研究中均采用上述的網格劃分策略和網格控制尺寸進行數值計算。

圖4 網格獨立性分析結果Fig. 4 Mesh independence analysis results

2.3 外流計算域的流動控制方程

在靜止參考系下求解靜態的外流計算域流動控制方程。在連續介質的前提下，計算域外流場流動應該滿足質量守恒方程、動量守恒方程，能量守恒方程。其中，質量守恒方程為

式中：t為時間；ρ為流體密度；v為速度矢量。

動量守恒方程為

式中：τij為黏性應力張量；g為重力加速度；F為外部體積力，如多相流相互作用力等。

能量方程為

式中：H為流體總熵；T為流體溫度；κ為流體的熱導率；E為流體的物質能量。

2.4 內流場計算域的流動控制方程

在旋轉參考系下求解內流計算域流動控制方程。靜止參考系和旋轉參考系的速度變換方程為

式中：vr為旋轉參考系下的速度矢量。

加速度變換方程為

式中：ω為旋轉參考系的旋轉角度， 為運動的角加速度；a為靜止參考系下的加速度；ar為旋轉參考系下的加速度。

將式(4)及式(5)代入式(1)，得到旋轉參考系下質量守恒方程為

將式(4)以及式(5)代入式(2)，得到旋轉坐標系下的動量守恒方程為

轉換坐標系后，能量方程的形式不變。

2.5 模型設置與求解工況

在建立靜止參考系以及旋轉參考系下的流動控制方程后，采用有限體積法對密閉空間內的三維旋轉流場進行求解。計算過程中發現，Coupled算法相較于分離算法具有更好的收斂性，因此，采用Coupled算法進行迭代計算。為了保證計算的精確性，迭代計算的時間步長為涵道旋轉周期的1/1 000，即當涵道轉速為60 r/min時，對應迭代時間步長為0.001 s。具體的模型求解設置如表2所示。

表2 模型求解設置Table 2 Model solution setting

3 密閉空間旋轉流場分布特性

3.1 空間流場的徑向分布特性

對密閉空間內的旋轉流場進行求解，得到某時刻計算域XOY截面速度分布如圖5所示。從圖5可以看出：涵道的旋轉運動將帶動密閉空間內的空氣隨之運動形成旋轉尾流，旋轉尾流大致沿旋轉運動的軌跡分布，并且逐漸向徑向外側擴散。大體上，尾流的速度在涵道周圍以及后部較大，然后沿涵道的運動軌跡逐漸減小。

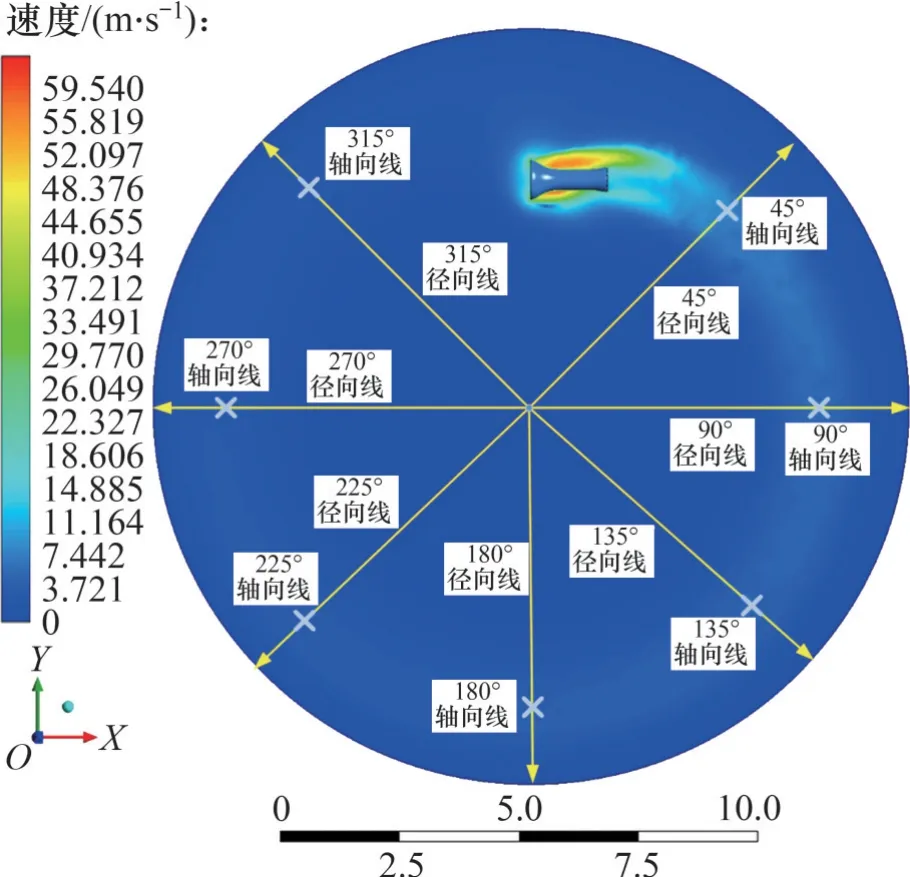
圖5 旋轉流場相對速度分布(XOY截面)Fig. 5 Distribution diagram of relative velocity of rotating flow field(XOY section)

為了進一步分析空間尾流的分布情況，在XOY截面內以旋轉中心為起點，建立數條放射性的徑向監測線(圖5)，其中，每條相鄰的監測線之間相差45°，規定每條監測線的方向均由旋轉中心指向外側。沿不同角度徑向監測線的速度分布如圖6所示。從圖6可以看出，沿各監測線，速度大致呈現出先增加后減小的趨勢。在靠近圓心的區域，速度很小；在旋轉尾跡部分，速度達到最大；在外壁面處，速度減小為0 m/s。由于離涵道太近，沿45°監測線，速度分布頂部呈現雙峰形式，除此之外其他角度的沿線速度都呈現出單峰的形式。

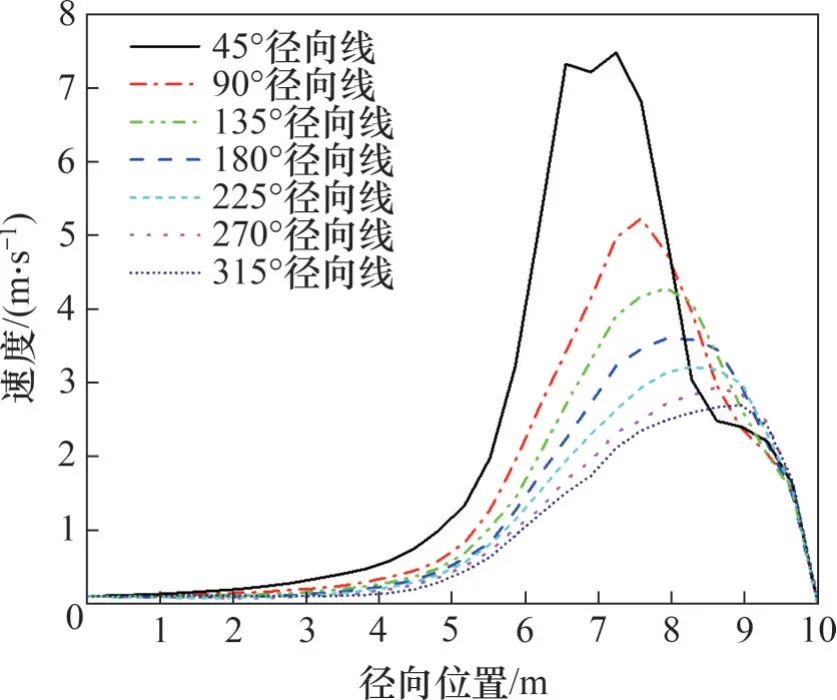
圖6 沿徑向監測線的速度分布Fig. 6 Velocity distribution along the radial monitoring line

3.2 空間流場的軸向分布特性

計算域XOZ截面的速度分布如圖7所示。從圖7可以看到：在涵道旋轉軌跡附近，密閉空間尾流的速度最大，在朝四周擴散的過程中已經到達了徑向和軸向的壁面處；旋轉徑向的尾流擴散效果要比旋轉軸向的擴散效果好。

圖7 旋轉流場相對速度分布(XOZ截面)Fig. 7 Distribution diagram of relative velocity of rotating flow field(XOZ section)

為了進一步研究軸向的尾流分布情況，根據徑向監測線建立軸向監測線。由于計算域上下的流場對稱分布，因此，軸向監測線只位于上半計算域。各軸向監測線起始于XOY中心截面內對應徑向監測線上尾流最大值出現的位置，一直延伸至軸向邊界處，其位置如圖5 中“×”號所示。沿不同角度軸向監測線的速度分布情況如圖8 所示。從圖8可以看出，不同角度監測線速度分布呈現相似的趨勢。當軸向坐標較小時，尾流速度較大，然后隨著軸向坐標的增大而逐漸減小。同時，當軸向位置較小時，不同角度的速度分布差異較大，但是隨著軸向位置的增加，不同角度的尾流速度的差異逐漸變小。當軸向坐標超過2.0 m之后，各角度的速度線基本上重合。

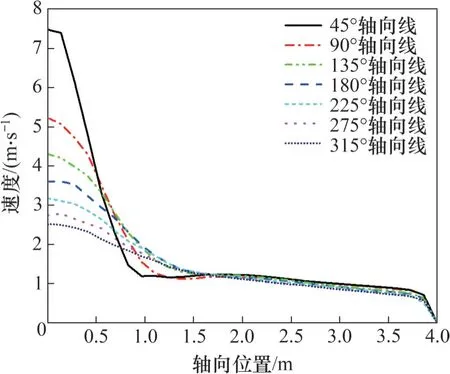
圖8 沿軸向監測線的速度分布Fig. 8 Velocity distribution along the axial monitoring line

綜上所述，旋轉帶動的空間尾流將對流場試驗產生影響，主要體現在空間尾流的尾跡會和涵道開口相接(轉速很小、旋轉半徑很大時則不會相接)，雖然此時空間尾流的速度已經衰減至較小，但是還是會減小涵道內的相對試驗速度，并且轉速越高、旋轉半徑越小，這種減速效果會越明顯。

3.3 試驗段內的流場分布

涵道內不同截面的速度分布如圖9所示。從圖9可以看出：涵道結構具有明顯加速效果，流體經過收縮段的收縮加速在試驗段內形成高速氣流，然后再通過擴散段降速流出涵道。此外，由于旋轉時內外圈相對速度的差異導致試驗段內XOY平面(旋轉徑向)的速度分布出現偏移，該現象由旋轉運動的特性導致，而在XOZ平面內并沒有類似情況的出現。

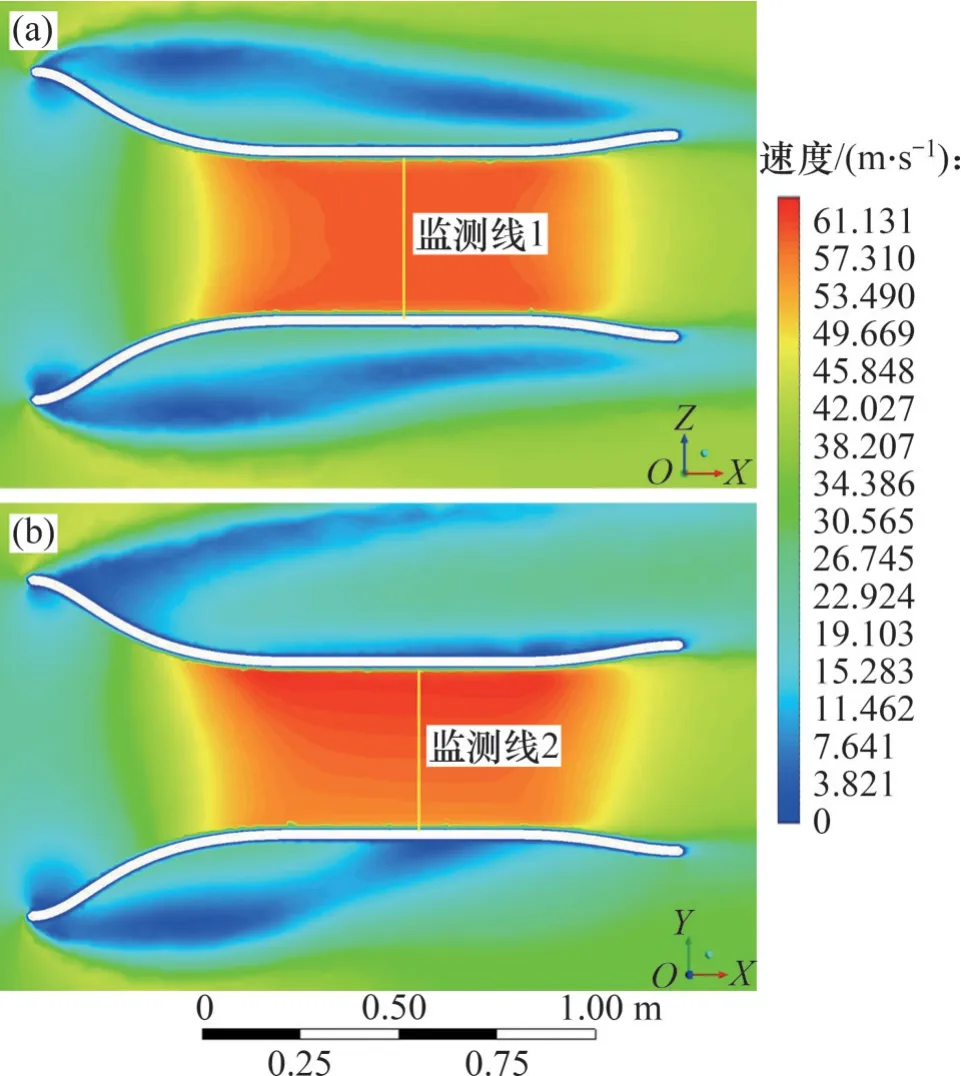
圖9 涵道內速度分布云圖Fig. 9 Cloud image of velocity distribution in culvert

在涵道試驗段中心處建立檢測線1以及檢測線2對試驗段內的速度分布進行進一步分析。沿監測線1 和檢測線2 的速度分布如圖10 所示。從圖10可以看出，除近壁面速度迅速減小的區域外，沿監測線1 速度則呈現出平穩的趨勢，而沿監測線2的速度隨著坐標的增大而逐漸增加；模型區內沿監測線2速度的最大值與試驗段平均氣流速度的相對誤差為7.25%，速度最小值與試驗段平均氣流速度的相對誤差為4.97%。

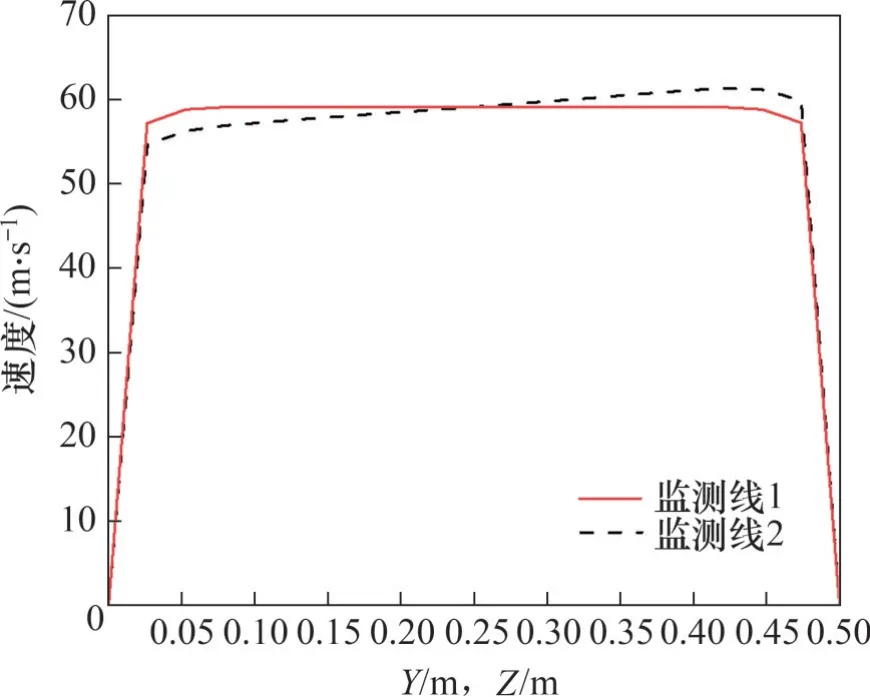
圖10 沿監測線1和監測線2的速度分布Fig. 10 Velocity distribution along monitoring lines 1 and 2

4 試驗段內的流速和流場品質特性

試驗段為氣流場試驗的核心區域，試驗段內的流速和流場品質將直接影響氣流場試驗效果以及所獲數據的準確性。本節將對涵道試驗段內的平均流速和流場品質進行分析，試驗段內的平均流速以及其他流場品質指標值均為試驗段內1 000個均勻取點相應參數的算術平均值。

4.1 收縮比對試驗段流速的影響

收縮段進出口面積之比稱為收縮比，收縮比與涵道加速效果直接相關。保持旋轉半徑為6 m，得到不同收縮比試驗段內的平均流速的變化如圖11 所示，圖11 中，運動線速度即為涵道中心處的旋轉線速度。從圖11 可以看出，涵道結構可以明顯提高試驗段內的平均流速，當轉速相同時，涵道試驗段的平均流速隨著收縮比的增大而增大。

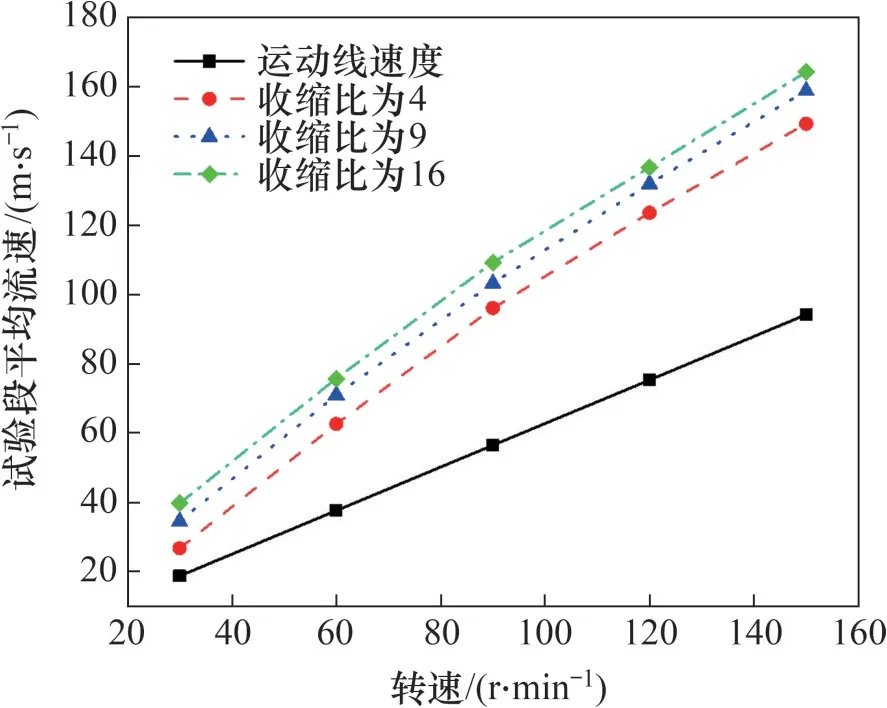
圖11 涵道收縮比對平均流速的影響Fig. 11 Effect of culvert contraction ratio on mean velocity

定義涵道試驗段平均流速相對于涵道中心處旋轉線速度的提高比例為涵道的加速效果k1，即

式中：va為試驗段平均流速；r為涵道旋轉半徑；n為涵道轉速，r/min。

保持旋轉半徑為6 m，計算得到不同轉速下k1與收縮比的關系，如圖12 所示。從圖12 可以看出，隨著收縮比的增加，k1逐漸增加，但是該增加趨勢呈現出飽和效應。這是因為當收縮比過大時，收縮段壁面的阻滯效應也會增大，這將會影響涵道內氣流的各向同性，甚至產生氣壁分離，導致加速效果下降，并且影響試驗流場品質[25]。因此，不能無限制的增加收縮比來增加試驗段內的流速。從圖12 還可以看出，當收縮比較小、轉速也較小時，k1也較小，說明此時并沒有完全發揮出涵道的加速性能，可以適當增加涵道轉速以獲得更合理的加速效果。采用加速涵道結構后，試驗段內平均氣流速度相較于旋轉線速度都有了明顯提升。可見采取涵道加速結構之后，可以以較低的轉速和較小的旋轉半徑獲得較大的氣流速度，極大地提高了基于旋轉運動氣流場試驗方法的試驗效率和可行性。

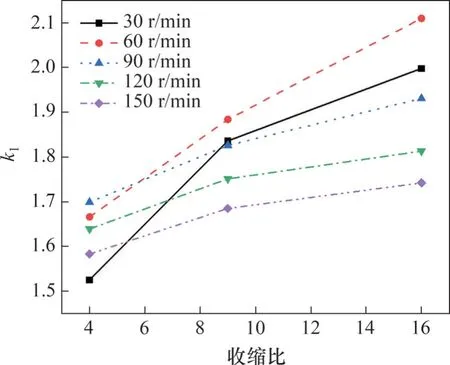
圖12 涵道收縮比對k1的影響Fig.12 Effect of culvert contraction ratio on k1

4.2 旋轉半徑和轉速對試驗段流速的影響

保持旋轉半徑為6 m，k1與轉速的關系如圖13(a)所示。從圖13(a)可以看出，隨著轉速的增加，k1呈現先增大后減小的趨勢。當收縮比為4 時，k1在轉速60 r/min 出現最大值；當收縮比為9 和16時，k1在90 r/min出現極大值，隨后均隨著轉速的增加而逐漸減小。該趨勢是旋轉尾流的影響所致；當轉速較小時，旋轉尾流也較小，不會對涵道入口的相對氣流速度造成影響，隨著轉速的增加，旋轉尾流逐漸增大，造成涵道入口處相對氣流速度的減小，進而導致試驗段內的平均速度減小，削弱涵道加速效果。

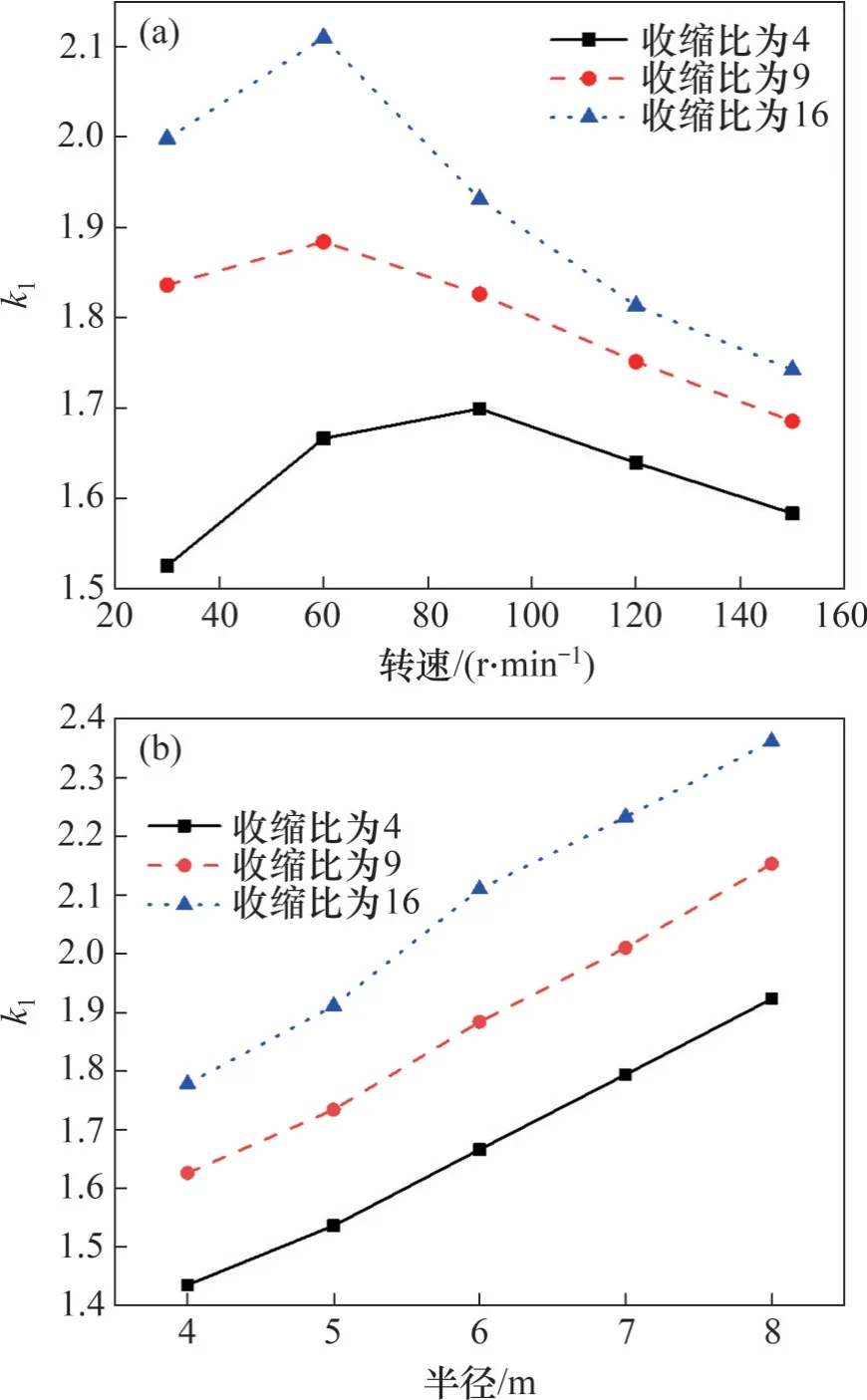
圖13 轉速和旋轉半徑對k1的影響Fig.13 Effect of speed and radius of rotation on k1

保持轉速為60 r/min，旋轉半徑對涵道加速效果的影響如圖13(b)所示。從圖13(b)可以看出：隨著旋轉的增加，k1呈現單調增加的趨勢。旋轉半徑的增加會減弱旋轉尾流對相對試驗速度的影響，因此，轉速越大涵道加速效果越明顯。同時，涵道旋轉半徑的增加還可以減小旋轉運動所導致的速度偏移，因此，從原理上來說，基于旋轉運動的氣流場產生方法中通過增加旋轉半徑的來提升試驗流速要比增加轉速更合理。

4.3 試驗段流場品質評價指標

基于旋轉運動的氣流場產生方法的最大誤差源自旋轉運動帶來的流場的不均勻性。在氣流場試驗中，與流場的均勻性評價有關的指標主要是動壓系數和氣流偏角，因此，本研究選擇對試驗段內的平均動壓系數以及平均氣流偏角進行計算評估[26-27]。

動壓系數反映的是流速的均勻性，本文將流場中某點的動壓系數定義為該點的動壓與模型區平均動壓的偏差。

式中：qi為某點的動壓；q為模型區的平均動壓。

氣流偏角反映的是方向場的均勻性，定義為該位置處的氣流的方向偏移主流方向的角度，即：

式中：βi為某點的氣流偏角，vx、vy和vz分別為流速沿x方向(主流方向)、y方向和z方向的分量。

理想情況下，動壓系數越小越好，其越接近于0，說明試驗段內速度場越均勻；試驗段內的平均動壓系數也是越小越好，其越接近于0，說明試驗段內氣流方向越均勻。

4.4 轉速對試驗段流場品質的影響

轉速對試驗段動壓系數以及氣流偏角的影響規律如圖14所示。從圖14可以看出：不同旋轉半徑時，動壓系數和氣流偏角隨著轉速的增加而增加，說明隨著轉速的增加，試驗段內的試驗流場品質逐漸降低。當轉速較小時，動壓系數和氣流偏角隨轉速的增加較為緩慢，說明此時轉速的增加對試驗流場品質的影響并不顯著；反之，轉速的增加將嚴重影響試驗段內的試驗流場品質。一方面，轉速的增加加劇了旋轉徑向相對試驗速度的差異，導致試驗段內的流場更加不均勻；另一方面，轉速的增加也加劇了密閉空間內旋轉尾流，進一步影響了試驗段內的流場品質，并且隨著轉速的增加，這種影響越來越明顯。因此，為了提升試驗流場品質，應該盡量減小轉速。

圖14 轉速對試驗流場品質的影響Fig.14 Effect of rotational speed on flow field quality

4.5 旋轉半徑對試驗段流場品質的影響

旋轉半徑對試驗段動壓系數及氣流偏角的影響如圖15 所示。從圖15 可以看出：不同轉速時，試驗段內的動壓系數和氣流偏角均隨著旋轉半徑的增加而減小，說明旋轉半徑的增加將有效提升試驗段內的試驗流場品質。一方面，旋轉半徑的增加減少了旋轉徑向相對試驗速度不均勻的情況；另一方面，旋轉半徑的增加也減弱的旋轉尾流的影響。因此，在成本允許的前提下，旋轉半徑越大越好，在極限情況下，旋轉半徑無限大時，試驗流場不均勻性的問題也不復存在了。

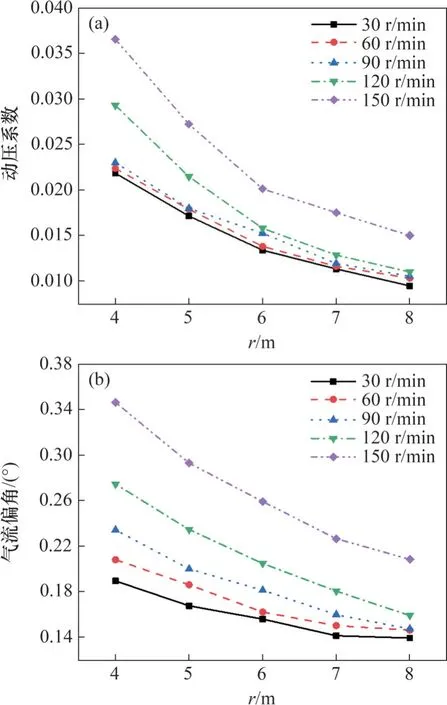
圖15 旋轉半徑對試驗流場品質的影響Fig. 15 Effect of rotation radius on flow field quality

以上對于轉速和旋轉半徑的討論均忽略了其對流速的影響。試驗段內的平均流速與轉速和半徑成正比，轉速太小則涵道內試驗流速達不到試驗要求，轉速太大則涵道內的試驗流場品質下降。而旋轉半徑的增大對于增加試驗流速和提升試驗流場品質均有利，但是會急劇增加試驗裝置體積和造價。因此，在試驗成本允許的條件下，通過增加旋轉半徑來提升試驗流速和試驗流場品質是最合理的方式。

5 結論

1) 有限空間內的旋轉尾流大致沿旋轉運動的軌跡分布，其速度逐漸減小的同時也在朝四周擴散，旋轉徑向的尾流擴散效果要明顯比旋轉軸向的好。

2) 涵道結構可以顯著提升試驗段內的平均流速。涵道的加速效果隨著涵道收縮比以及旋轉半徑的增加而增加，隨著轉速的增加先增加后減小。

3) 試驗段內的平均動壓系數以及氣流偏角隨著轉速的增加而增加，隨著旋轉半徑的增加而減小。通過增加旋轉半徑來提升試驗流速和試驗流場品質是最合理的方式。

4) 在基于旋轉運動的試驗氣流場產生方法中，旋轉運動線速度的差異將使涵道內的流場分布出現徑向偏移，嚴重影響試驗段內的試驗流場品質。后續研究中需要探索相應校正方法以進一步提升試驗內的流場均勻性，使其符合更高精度流場試驗的要求。