毫米波大規(guī)模MIMO系統(tǒng)混合連接天線結(jié)構(gòu)的混合預(yù)編碼算法研究
周 圍 馬茂瓊* 陳星宇 冉靖宣 彭 洋
1(重慶郵電大學(xué)通信與信息工程學(xué)院 重慶 400065) 2(重慶郵電大學(xué)移動通信技術(shù)重慶市重點實驗室 重慶 400065)
0 引 言
相較于當前的4G系統(tǒng),5G蜂窩網(wǎng)絡(luò)將提供超高速連接和更高的數(shù)據(jù)速率,并具有更強大的可靠性、更高的頻譜效率和更低的能耗[1]。毫米波通信和大規(guī)模MIMO系統(tǒng)的結(jié)合,被認為是提高未來5G無線通信系統(tǒng)吞吐量極具潛力的候選方案[2]。
毫米波和大規(guī)模MIMO技術(shù)相結(jié)合將為5G系統(tǒng)帶來更大的可用帶寬和更高的天線增益。但是毫米波大規(guī)模MIMO技術(shù)的實際應(yīng)用也存在著許多巨大的挑戰(zhàn),比如導(dǎo)頻數(shù)量有限、信號處理復(fù)雜度高、硬件成本和功耗等。近年來,為了解決這些問題,預(yù)編碼已經(jīng)成為當下重要的研究方向。
全數(shù)字預(yù)編碼能夠獲得預(yù)編碼的最佳性能,但是硬件成本昂貴、功耗太高(主要是射頻鏈路的功耗和成本都較高);模擬預(yù)編碼則是犧牲性能(減少射頻鏈路)來降低硬件成本和功耗[3],而大規(guī)模MIMO中龐大的天線數(shù)量使得全數(shù)字預(yù)編碼不再適用,模擬預(yù)編碼無法滿足5G系統(tǒng)對傳輸性能的要求。在此背景下,低成本、低功耗的混合預(yù)編碼(射頻域采用模擬預(yù)編碼,基帶采用數(shù)字預(yù)編碼)被提出,其性能接近全數(shù)字預(yù)編碼,但是對射頻鏈路數(shù)量的需求降低很多。目前,混合預(yù)編碼的硬件實現(xiàn)廣泛采用全連接天線結(jié)構(gòu)和部分連接天線結(jié)構(gòu)。然而,當前的研究也表明了這兩種結(jié)構(gòu)難以同時滿足5G更高速率和更低能耗的要求。
最近,又有研究者提出一種混合連接天線結(jié)構(gòu)[4]如圖1所示。參考文獻[4]的研究結(jié)論表明混合連接天線結(jié)構(gòu)能減少功率消耗和硬件成本,因此更適合5G系統(tǒng)。混合連接天線結(jié)構(gòu)整體可視為一個部分連接天線結(jié)構(gòu),每一個子連接天線結(jié)構(gòu)又可視為一個全連接天線結(jié)構(gòu),因此該結(jié)構(gòu)在能量效率和頻譜效率之間可以達到更好的平衡,而全連接天線結(jié)構(gòu)和部分連接天線結(jié)構(gòu)則可以視為混合連接天線結(jié)構(gòu)的特殊形式[4]。但是,當下研究混合連接天線結(jié)構(gòu)的混合預(yù)編碼算法極少,且文獻[4]基于連續(xù)干擾相消(Success Interference Cancellation,SIC)思想所提出的算法流程繁瑣。為了簡化算法流程,本文首次提出將混合連接天線結(jié)構(gòu)的信道矩陣分解一系列子信道矩陣,然后分別對每一個子信道矩陣求解最優(yōu)混合預(yù)編碼矩陣的思想。混合連接的結(jié)構(gòu)特點表明求解每一個最優(yōu)混合預(yù)編碼子矩陣可視為求解一個全連接天線結(jié)構(gòu)的最優(yōu)混合預(yù)編碼矩陣。

圖1 單用戶混合連接天線結(jié)構(gòu)模型
目前,全連接天線結(jié)構(gòu)的混合預(yù)編碼方案眾多,文獻[5]提出正交匹配追蹤算法(Orthogonal Matching Pursuit,OMP),該算法利用了毫米波信道的稀疏特性來降低混合預(yù)編碼的復(fù)雜度,而且可以得到接近全數(shù)字預(yù)編碼算法的性能。文獻[6]提出相位提取交替最小化算法(Phase Extraction Alternating Minimization,PE-Alt),該算法能實現(xiàn)比OMP算法更高的頻譜效率,但是復(fù)雜度更高。文獻[7]在交替最小化算法的基礎(chǔ)上進行改進,提出Alt-IMD,更進一步提高算法性能并降低算法復(fù)雜度。另外,還有混合塊對角化算法[8]、最小歐氏距離混合預(yù)編碼器[9]、最小均方差預(yù)編碼[10]等。本文結(jié)合混合連接天線結(jié)構(gòu)和Alt-IMD算法提出適用于混合連接天線結(jié)構(gòu)的基于迭代的矩陣分解預(yù)編碼方案(Hybrid Connected Structure AltIMD,HCS-AltIMD),仿真結(jié)果表明本文算法不僅能獲得高頻譜效率還可以獲得高能量效率。
1 系統(tǒng)模型
1.1 混合連接天線結(jié)構(gòu)模型
毫米波大規(guī)模MIMO系統(tǒng)單用戶混合連接天線結(jié)構(gòu)模型如圖1所示,發(fā)射端Ns個數(shù)據(jù)流經(jīng)過Nt個發(fā)射天線發(fā)射,經(jīng)由信道傳輸?shù)接蠳r根接收天線連接的接收端。發(fā)射端包括D個RF鏈子陣列,每個RF鏈子陣列包括S個RF鏈路,且對應(yīng)一個天線子陣列,該天線子陣列包括N個發(fā)射天線,因此發(fā)送端共有SD個RF鏈,DN個發(fā)射天線,且滿足Ns≤SD≤Nt。我們用NRF表示總RF鏈數(shù)目,Nt表示總天線數(shù)目,為了簡化模型,本文假設(shè)數(shù)據(jù)流數(shù)目等于RF鏈數(shù)目,即Ns=NRF≤Nt。

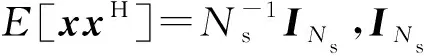
1.2 信道模型
在毫米波大規(guī)模MIMO信道條件下,文獻[11]提出了窄帶簇信道模型(基于擴展的Saleh-Valenzuela模型),可以精確獲得毫米波信道的特征。文獻[12]的研究結(jié)果表明,毫米波信道包括Ncl個散射簇,且每個簇貢獻Nray條傳輸路徑,這些散射簇的和構(gòu)成了信道矩陣H。因此,窄帶信道矩陣H可以被表示為:

假設(shè)均勻線陣中包括N個天線元件,那么陣列響應(yīng)矢量可以表示為:
式中:d為陣元間距,一般取半波長,即d=λ/2,λ表示波長。
假設(shè)均勻面陣的平面的各邊分別有W1和W2個天線元件,且N=W1W2,則陣列響應(yīng)矢量可以表示為:
式中:0≤p 均勻線陣結(jié)構(gòu)簡單,但在相同的天線元件數(shù)目的條件下均勻面陣更易于小型化和裝配,且能產(chǎn)生3D波束。故本文采用均勻面陣。 本節(jié)建立混合連接天線結(jié)構(gòu)的優(yōu)化目標,本文以最大化頻譜效率為標準來設(shè)計模擬預(yù)編碼矩陣FRF和數(shù)字預(yù)編碼矩陣FBB。根據(jù)文獻[13],當發(fā)射信號為高斯信號時,可達的頻譜效率可以表示為: (1) 因此本文的優(yōu)化目標可以表示為: 本文采用混合連接天線結(jié)構(gòu),因此FRF可以寫為[14]: FRF=diag[FRF1,FRF2,…,FRFD] (2) 式中:FRFi∈CN×S表示第i個RF鏈子陣列相應(yīng)的模擬預(yù)編碼子矩陣。 將數(shù)字預(yù)編碼矩陣FBB和信道矩陣H分別寫為: (3) H=[H1,H2,…,HD] (4) 式中:FBBi∈CS×Ns表示FBB中與第i個RF鏈子陣列相連的數(shù)字預(yù)編碼子矩陣;Hi∈CNr×N表示第i個信道子矩陣。 假設(shè)數(shù)字預(yù)編碼矩陣FBB各列正交[6],即: (5) 則矩陣各行也正交,即: (6) 將式(2)-式(6)代入式(1): (7) 文獻[6]的研究結(jié)果可知,最大化式(7)等效于最小化FRFiFBBi和Fopti之間的歐氏距離,因此本文的優(yōu)化目標可以被表示為: (8) FRFi(m,n)∈F?m,n 由于式(8)的非凸約束,直接優(yōu)化式(8)是不切實際的。大量的研究者針對式(8)提出不同優(yōu)化算法,如文獻[5]的OMP算法和文獻[6]的PE-Alt算法等,文獻[7]所提出的Alt-IMD算法則是在PE-Alt算法的基礎(chǔ)上進行改進,相比于PE-Alt算法,該算法不僅提升了頻譜效率還降低了運算復(fù)雜度。Alt-IMD算法如算法1所示。 算法1Alt-IMD混合預(yù)編碼算法 1.輸入:Fopt,最大迭代次數(shù)iterations。 2.輸出FRF和FBB。 3. 初始化臨時矩陣Ftemp=Fopt,并令k=0 4.如果k≤iterations,進行以下步驟,否則跳轉(zhuǎn)到步驟8 8.k=k+1 根據(jù)前文的表述,本文算法思想是將信道矩陣拆解為D個子信道矩陣,然后分別對每一個子信道矩陣采用文獻[7]所提出的Alt-IMD算法求解最優(yōu)混合預(yù)編碼矩陣。混合連接天線結(jié)構(gòu)的HCS-AltIMD算法如算法2所示。 算法2HCS-AltIMD混合預(yù)編碼算法 1.輸入:H,D,N。 2.輸出:FBB和FRF。 3.初始化i=1,FBB=[],FRF=[] 4.如果i 5.Hi=H[:,(i-1)N+1:iN] 6.[U,Σ,VH]=svd(Hi) 7.Fopti=V[1:N,1:Ns] 8.調(diào)用Alt-IMD算法求解FRFi和FBBi 9.FBB=[FBB;FBBi] 10.FRF=diag[FRF;FRFi] 11.i=i+1 HCS-AltIMD算法首先通過矩陣分解極大地降低了混合預(yù)編碼設(shè)計流程的難度,然后依次對單個子連接天線結(jié)構(gòu)采用Alt-IMD方案設(shè)計混合預(yù)編碼矩陣就可以得到較高的算法性能。 能量效率[6]定義為: 式中:能量效率的單位是bit/s/Hz/J,Pt是發(fā)射總功率;PRF、PPA和PPS分別是單個RF鏈、單個移相器和單個功率放大器消耗的功率。而混合連接天線結(jié)構(gòu)、全連接天線結(jié)構(gòu)和部分連接天線結(jié)構(gòu)的主要區(qū)別在于移相器的數(shù)目。這三類天線結(jié)構(gòu)的移相器數(shù)目分別表示為: 下面主要對全連接的Alt-IMD算法、混合連接HCS-AltIMD算法和全連接的OMP算法的復(fù)雜度進行分析,結(jié)果如表1所示。 表1 算法復(fù)雜度比較 可以看出,OMP算法的復(fù)雜度最低,Alt-IMD算法次之,而造成HCS-AltIMD算法復(fù)雜度高于完全連接的Alt-IMD算法的主要原因是各個子信道矩陣的SVD分解。 這一部分通過對比最優(yōu)無約束預(yù)編碼算法、全連接Alt-IMD算法、部分連接Alt-IMD算法、OMP算法和HCS-AltIMD算法之間的頻譜效率,來說明本文算法的性能。其中最優(yōu)無約束預(yù)編碼算法作為全數(shù)字預(yù)編碼能實現(xiàn)預(yù)編碼最高的頻譜效率。其他的三種算法代表了全連接結(jié)構(gòu)和部分連接結(jié)構(gòu)能達到較高頻譜效率的混合預(yù)編碼算法。圖2對比了上述五種算法在不同RF鏈數(shù)目下的頻譜效率隨SNR變化的曲線(NRF=Ns)。可以看出,五種算法的頻譜效率都隨著數(shù)據(jù)流數(shù)目增加而增加。本文提出HCS-AltIMD算法的頻譜效率接近全連接的Alt-IMD算法,優(yōu)于全連接的OMP算法,且遠遠優(yōu)于部分連接天線結(jié)構(gòu)的Alt-IMD算法。 圖2 發(fā)射端RF鏈路數(shù)目等于數(shù)據(jù)流數(shù)時頻譜效率隨SNR變化曲線 圖3表示在不同的收發(fā)端天線數(shù)目下頻譜效率隨著SNR變化的曲線。可以看出,當NRF=Ns=8時,頻譜效率隨著收發(fā)端的天線數(shù)目的增多而提升。混合連接天線結(jié)構(gòu)的HCS-AltIMD算法的頻譜效率優(yōu)于全連接天線結(jié)構(gòu)的OMP算法,僅次于全連接天線結(jié)構(gòu)的Alt-IMD算法。 圖3 不同的收發(fā)端收發(fā)天線數(shù)目頻譜效率隨SNR變化曲線 圖4對比了混合連接天線結(jié)構(gòu)、全連接天線結(jié)構(gòu)和部分連接天線結(jié)構(gòu)在不同的RF鏈路數(shù)下的能量效率,可以看出當NRF=Ns時,部分連接天線結(jié)構(gòu)的能量效率隨著RF鏈路的數(shù)目增大逐漸優(yōu)于全連接天線結(jié)構(gòu),而混合連接天線結(jié)構(gòu)的能量效率則遠遠優(yōu)于前兩種連接天線結(jié)構(gòu)。 圖4 三種天線連接結(jié)構(gòu)能量效率隨RF鏈路數(shù)目變化的曲線 本文提出一種針對混合連接的交替迭代算法,通過將混合連接天線結(jié)構(gòu)劃分為一系列子連接天線結(jié)構(gòu),將每個子連接天線結(jié)構(gòu)視為一個全連接天線結(jié)構(gòu),極大地簡化了算法流程;然后分別對每個子連接天線結(jié)構(gòu)引用Alt-IMD算法,利用該算法的低復(fù)雜度和接近最優(yōu)無約束預(yù)編碼的頻譜效率的優(yōu)勢,在保證算法高頻譜效率的同時極大地降低了運算復(fù)雜度。另外,混合連接天線結(jié)構(gòu)融合了當下兩種主流結(jié)構(gòu)的優(yōu)勢,在獲得高頻譜效率的同時保證了高能量效率。仿真結(jié)果顯示,HCS-AltIMD算法的頻譜效率優(yōu)于全連接天線結(jié)構(gòu)的OMP算法,更加接近全連接天線結(jié)構(gòu)的Alt-IMD算法,且能量效率優(yōu)于全連接天線結(jié)構(gòu)和部分連接天線結(jié)構(gòu)。2 HCS-AltIMD混合預(yù)編碼算法
2.1 優(yōu)化目標

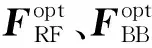
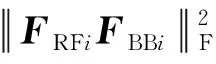

2.2 算法原理
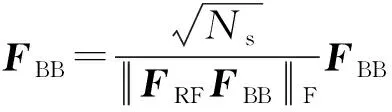
2.3 能量效率
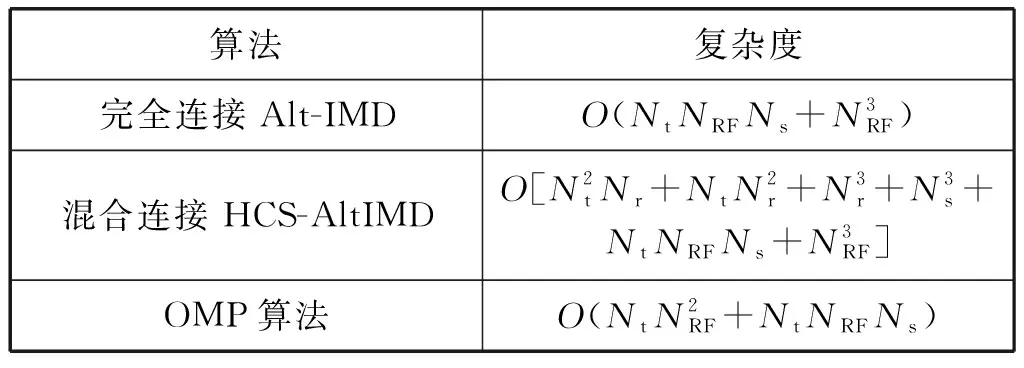
3 復(fù)雜度與仿真結(jié)果分析
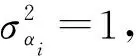
3.1 復(fù)雜度分析
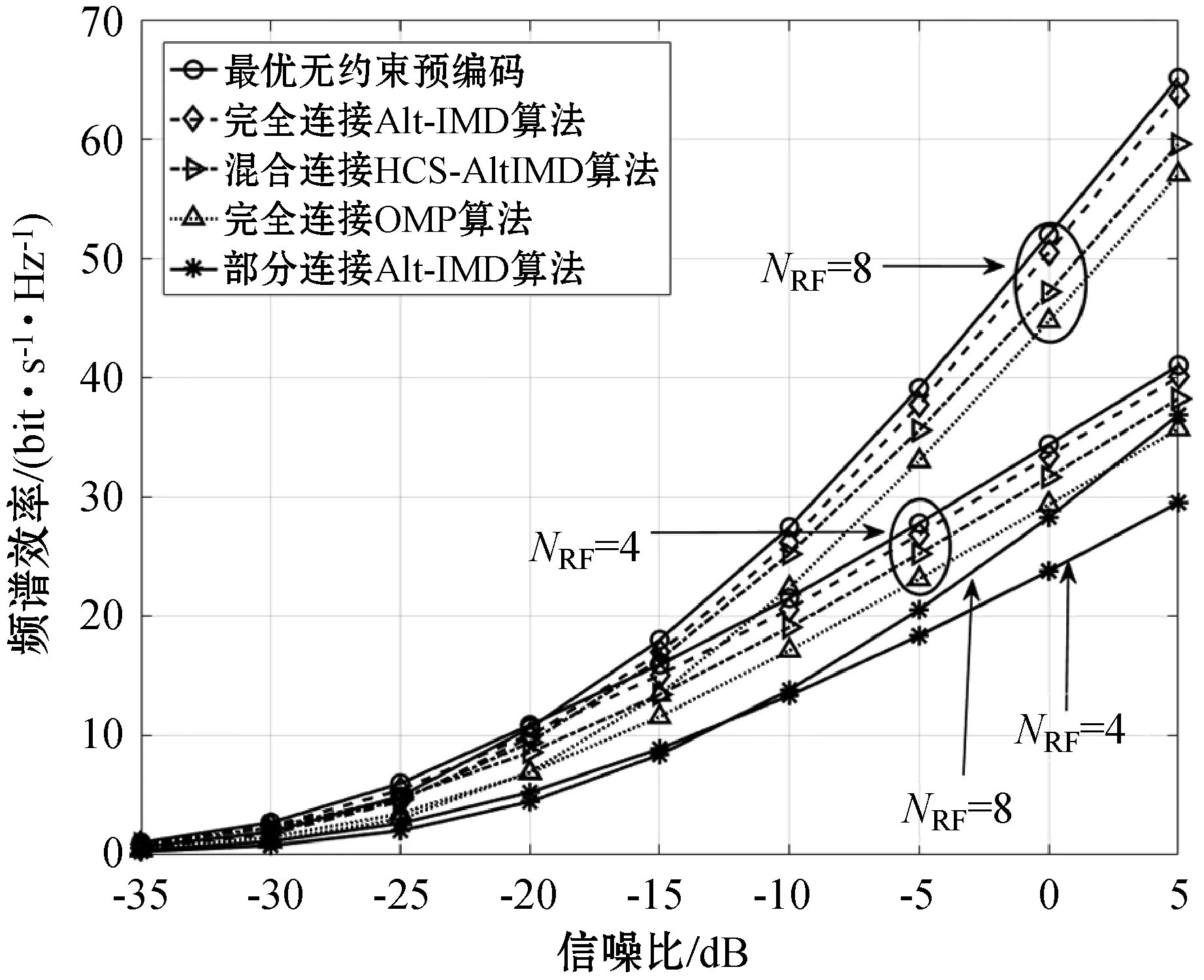
3.2 頻譜效率仿真
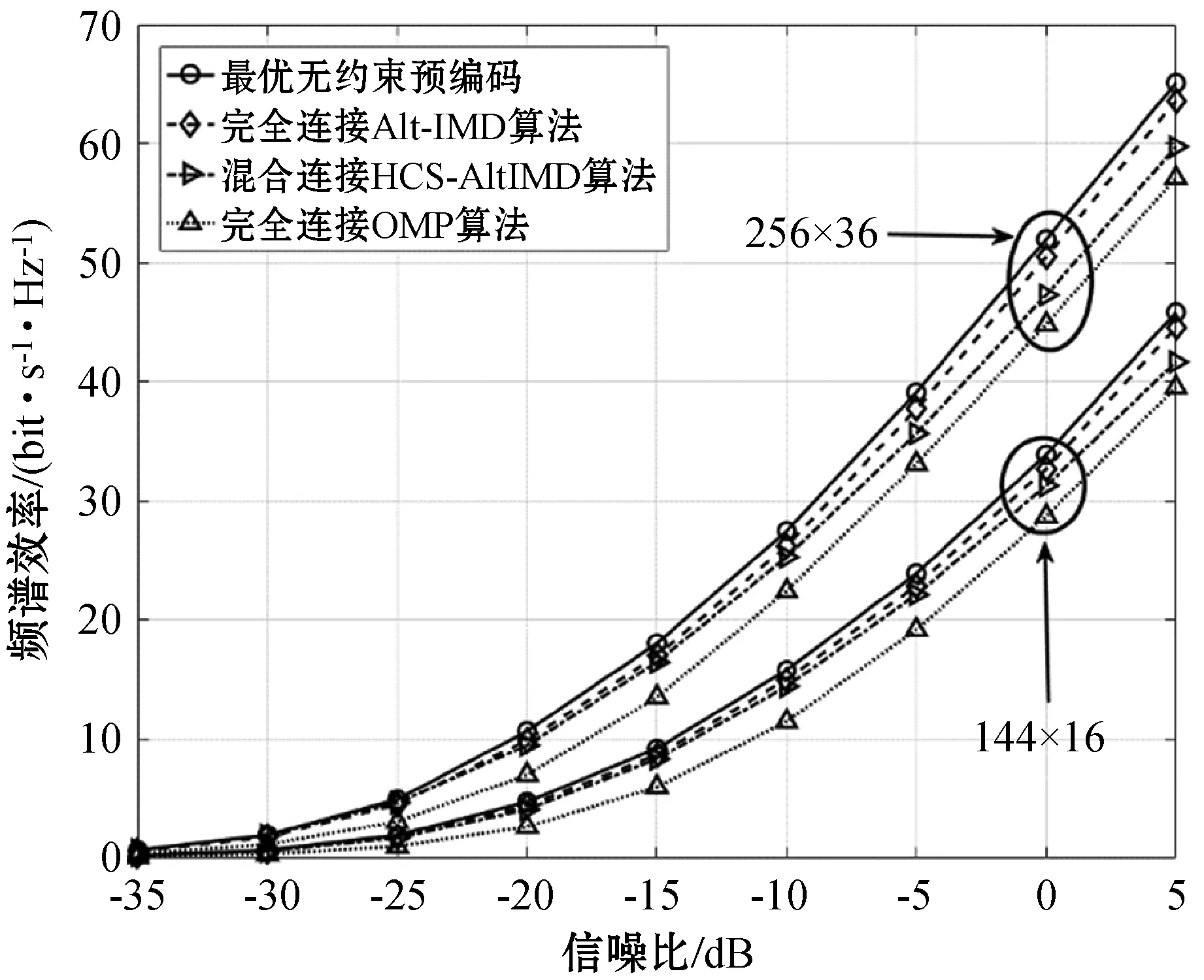
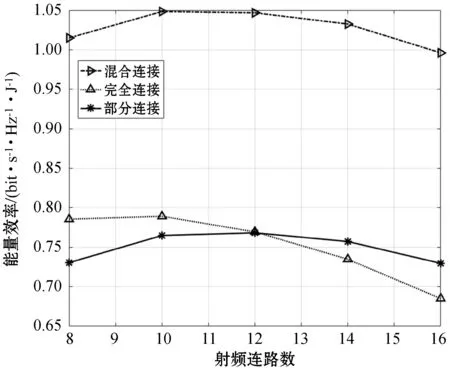
3.3 能量效率仿真
4 結(jié) 語

