基于ST-ACF與MALST-ACF模型的城市道路時空相關性研究

陳玉飛　黨倩　陳愛偉

摘 要：交通流時空特征的識別對交通擁堵的疏導決策具有重要意義。文章根據城市道路網絡的交通流特性，分別從全局和局部研究城市交通擁堵在時間維度和空間維度的變化特征，引入空間延遲算子，提出了基于多元鄰接關系的時空相關性度量方法。首先，文章分析了道路網絡交通流的時空特性，建立了適用于城市道路網絡的空間鄰接矩陣；其次，基于ST-ACF函數（Spatio-temporal autocorrelation function）計算全局路段相關程度、基于改進后的MALST-ACF函數（Multivariate adjacent local spatiotemporal correlation function）計算局部路段相關程度；最后，結合唐山市24條路段的交通流量數據驗證了路網間存在顯著時空相關性，并且這種時空相關性具有時間動態、空間異質等特點。

關鍵詞：城市交通；時空相關性；擁堵擴散；空間延遲算子；鄰接矩陣

中圖分類號：F542；U491.1文獻標志碼：ADOI：10.13714/j.cnki.1002-3100.2023.02.003

Abstract： The recognition of spatiotemporal characteristics of traffic flow is of great significance to the decision-making of easing traffic congestion. According to the traffic flow characteristics of the urban road network， this paper studies the change characteristics of urban traffic congestion in the time and space dimensions from the global and local perspectives， introduces the spatial delay operator， and proposes a spatial-temporal correlation measurement method based on multiple adjacencies. Firstly， the paper analyzes the space-time characteristics of the traffic flow of the road network， and establishes the spatial adjacency matrix applicable to the urban road network. Secondly， the global link correlation degree is calculated based on the ST-ACF function （spatio-temporal autocorrelation function）， and the local link correlation degree is calculated based on the improved MALST-ACF function （multivariate adjacent local spatiotemporal correlation function）. Finally， combined with the traffic flow data of 24 road sections in Tangshan City， it is verified that there is significant spatiotemporal correlation between the road networks， and this spatiotemporal correlation has the characteristics of temporal dynamics and spatial heterogeneity.

Key words： urban traffic; spatio-temporal correlation; congestion diffusion; spatial delay operator; adjacency matrix

隨著城市機動車保有量的不斷增加，交通擁堵已成為城市交通亟待解決的迫切問題，嚴重影響人們的出行效率，極易引發交通事故。受城市空間分布及人們的通勤出行影響，交通擁堵存在潮汐性、區域連鎖性等時空特征，實現交通流時空特征的精細化識別及管理是城市管理部門進行交通治理的重要手段，對交通擁堵的疏導決策具有重要意義。對此，本文面向路網交通流的時空關聯特征，通過構建交通流時空相關性模型實現路網交通流建模分析，實現對路網交通時空特征的精細化描述，為路網短時交通預測及交通誘導提供依據。

國內外學者對時空相關性已開展了大量研究，其中利用指數研究來揭示時空相關性的變化特征的手段已取得了豐富的技術應用。例如，陳紹寬等[1]通過引入時空對象對傳統的指數進行改進，實現時空指數的實際應用價值；韋偉等[2]運用時空散點圖對城市道路時空關聯性進行分析，并利用聚類算法揭示交通狀態；代偵勇等[3]利用半變異函數對時空特性加以分析，得到全國降水量的分布特征；Chenhua Shen為了測試時空非平穩序列的時空相關度，提出了新時空趨勢下的全局和局部時空指數（TDGSTI和TDLSTI），發現TDGSTI揭示了時空對象的自相關水平。

上述研究在運用指數或改進指數的基礎上，在時間維度上有了進一步拓展，對時空特性進行了更加有效的分析，但在復雜路網交通條件下，模型計算結果的準確性較差[4]。

基于此，本文提出了一種多元鄰接的時空相關性度量方法，從宏觀和微觀兩個角度切入，在引入空間延遲算子定義后分別在全局和局部兩個方向對時空相關性的變化特征進行了詳細分析；最后通過案例分析得出的結論驗證了本文提出的方法的適用性。

1? ? 空間權重矩陣

城市道路交通流量具有明顯的時空特性，為了描述路網空間鄰接關系，需要對城市道路交通網絡中的路段空間位置的物理關系進行度量。本文使用時空自相關函數研究城市交通流量在時間和空間上的變化特征，利用空間拓撲學相關理論構建城市路網空間鄰接矩陣[5]。城市路網空間鄰接矩陣的建立是對路網交通流的時空相關性進行研究和分析的基礎。對于一個包含n個空間單元的研究對象，其空間鄰接矩陣W如公式（1）所示。

式中，Wij為空間鄰接矩陣W中空間對象i與空間對象j之間鄰接關系的權重值。

研究復雜網絡的拓撲結構時，復雜網絡的連接關系通常用G=（N，E）的形式來表示，其中N=（n1，n2，...，nm）表示網絡中節點的集合，E=（l1，l2，...，ln）表示邊的集合。實際應用中要根據不同的空間對象類型采用不同的鄰接關系。通常情況下，鄰接矩陣由以下兩種方法建立。

第一，圍繞空間關系中的節點進行分析。如果兩個節點n1和n2之間存在共同的邊l，那么節點n1和n2存在一階鄰接關系，視為直接相鄰。

第二，圍繞空間關系中的邊進行分析。如果邊l1和l2之間存在共同n點，那么邊l1和l2存在一階鄰接關系，視為直接相鄰。

根據上述方法可以建立網絡一階鄰接關系，二階及以上高階鄰接是由上一階進行鄰接迭代而來的，高階鄰接矩陣為在前一階基礎上鄰接的下一階。

本文以采集的城市道路交通流量數據為研究對象，通過建立以邊為對象的路網空間鄰接矩陣，以時空相關函數形式分析各路段與周邊路段交通狀態的相互影響程度。

描述物體的空間關系一般采用二進制方法，命名為二元矩陣。二元矩陣中只有數字0和1，數字0代表空間對象之間不存在鄰接關系，反之，數字1代表空間對象之間存在鄰接關系。

城市道路路網主要由路段和交叉點組成，在空間拓撲關系中表現為點和線段。研究靜態網絡拓撲結構時可以把城市道路路網看作無向圖；研究動態道路交通流量時可以把城市道路路網看作有向圖。城市道路網絡結構既不能被視為無向圖也不能被視為簡單的有向圖，由于其自身特殊結構導致路網的空間鄰接矩陣一般與有向圖的鄰接矩陣會有不同之處，其具體表現為以下兩個方面。

第一，交通流一般為上游流向下游，城市道路一般為雙向車道，所以交通流互為影響。如果城市道路表現為流暢狀態，那么道路交通流量一般從上游路段流到下游路段；如果城市道路表現為擁堵狀態，那么下游路段的交通流量會反作用于上游路段的交通流量。

第二，如果多條道路的車流量同時流向同一條道路，那么路段與路段之間將會相互作用，如圖1所示。

圖1中在道路暢通狀態時，車流量從上游路段1流向下游路段3，而在道路擁堵狀態或上游路段1車流量過大時，路段3的交通狀態將會直接受到影響，路段3的交通狀態受到影響后又會反作用于路段2。此時路段2與路段3為間接相互影響，建立二階鄰接關系。因此，圖2中，路段1與路段3、路段4建立直接影響關系，為一階鄰接關系；路段1與路段2建立間接影響關系，為二階鄰接關系。

基于城市道路交通流的路段時空流相互影響的特性，給定一個路段的城市交通空間鄰接網絡，建立基于路段交通流的一階、二階的空間鄰接矩陣，如圖2所示。

2? ? ?路網交通流時空相關性模型

2.1? ? ?全局度量指標

相關性是用來定義指標之間的相關程度的常用工具，本文采用時空自相關函數（Spatio-temporal autocorrelation function， ST-ACF）對城市道路路網在時間和空間兩個維度的相關程度進行描述[6]，通過全局時空相關性系數度量路段的相關程度。

在通常情況下，路網中的路段之間往往會出現一條路段對應多個階相鄰路段的情況，因此在計算全局時空自相關度量指標前需引入空間延遲算子的定義如式（3）和式（4）。

式中，L（l）為路網的階空間延遲算子；xi（t）為路網中路段i在j時刻的交通流觀測值；W（l）ij為路網l階空間權重矩陣中i路段和j路段之間的權重值。

所有的i和W（l）ij都不為0，且i路段和j路段滿足階鄰接時有如下公式。

使用上述介紹的空間延遲算子的定義，在同一時間延遲為s的情況下，任意路段的加權l階鄰接與同一路段的k階鄰接之間的平均協方差為

式中，γlk（S）為時間延遲S處l階和k階鄰接之間的時空協方差；N為研究路網中路段數；t為當前時間；S為時間延遲；E為數學期望；用向量表示法表示時空協方差為

式中，W（l）為研究路網中的l階空間權重矩陣（N×N）；X（t）為N×1列向量，表示t時刻路網中路段的交通流觀測值。

時空協方差函數的樣本估計γlk（S），也可通過式（7）直接估算為

由于存在多種可能標度，時空自相關的定義并不像單變量域那么簡單。在給定的城市區域道路路網中，l階和k階鄰接在當前t時間下延遲了S時刻的時空自相關系數可以表達為

公式（9）所定義的時空自相關系數是優選的，因為它的樣本估計方差對于所有空間延遲都已顯示為相對恒定。時空自相關系數的樣本估計很自然地遵循以下公式。

從公式（10）可以看出時空自相關函數（ST-ACF）的取值范圍為[-1，1]。當l=0時，定義任意路段0階（自身）與該路段k階鄰接的空間延遲為h，ST-ACF的分析結果可視為城市路網在時間延遲為S、空間延遲為h的情況下時空相關性變化特征。

2.2? ? 局部度量指標

交通流量一般指上游至下游車輛的積累，但受交通信號及其他流的加入（或離開）等交通系統內外部因素的影響，上游交通流向下游移動時通常會經歷增加或衰減。下游交通流在很大程度上受上游交通流的制約。因此，亟需對上游和下游交通流量的關系進行研究，一般需要考慮以下兩方面。

上游交通流到達下游位置的時長；

上游交通流對下游交通流的貢獻量。

為計算上游交通流量到達下游的時長，Petty提出了一種擬合長度窗口方法表征交通流量、速度和占有率之間的關系。但該方法受參數限制，當參數獲取困難或獲取數據存在較大誤差時，無法計算得到準確結果。

Vlahogianni利用遺傳算法（GA）挖掘上、下游交通流之間的關系，但該方法局限于通過數值迭代方式獲取相對空間關系，無法提供交通流的固定空間關系。

交叉關聯函數（Cross correlation function， CCF）可用于衡量一定范圍內兩個存在時間差的空間對象之間的相關性；由于其精確確定信號到達時間差、檢測嘈雜信號中已知信號的能力，該方法在研究單條道路上、下游交通流之間的相關性時能夠較好地表征二者之間的關系，同時該方法也廣泛適用于模式識別、信號檢測、氣象、和環境科學等領域。

CCF假設給定任意2個時間序列X和Y，移動一個或多個時間段產生Y，2個序列在給定時間延遲S下的時空相關系數可表示為式（11）。

式中，ρxy（S）為在時間延遲S下時間序列X和Y的相關函數；γxy（S）為在時間延遲S下時間序列X和Y的互協方差系數；σ2x，σ2y分別是時間序列X和Y的方差。現有如下兩個公式。

式中，μx，μy分別是時間序列X和Y的均值；x（t）為一定時間間隔內上游路段車流量的觀測值；x（t+s）為在時間延遲S后，上游路段車流量的觀測值；y（t+s）為在時間延遲S后，下游路段車流量的觀測值。

2.3? ? 基于多元鄰接關系的局部度量指標

由于城市路網中上、下游路段間多為一對多、多對多的鄰接關系，CCF只能度量給定區域內單條路段上、下游之間的相關性，無法計算復雜路段的空間關系。因此，本文結合空間延遲算子提出一種基于多元鄰接關系的局部時空自相關指數（Multivariate adjacent local spatiotemporal correlation function， MALST-ACF）。

式中，ζi（k，S）為路段i與其所有k階鄰接路段在時間延遲S下的局部時空相關性系數；T為統計時間段；S為時間延遲；xi（t）為路段i在t時刻的交通流樣本值；xi為路段的交通流數據在統計時間段T內的平均值；L（k）xi（t+s）為路段i在t時刻所有k階鄰接路段在t+s時刻的交通流之和，其計算公式同式（10）；L（k）xi為路段i所有k階鄰接路段交通流之和在統計時段內的平均值。

MALST-ACF從路段角度出發描述路段之間在一定空間延遲和時間延遲下的時空相關性變化特征。相比于CCF函數，MALST-ACF不僅可用于分析路段上、下游之間的時空相關性，還可用于分析路段自身與其階鄰接路段之間的時空相關性。

3? ? 案例分析

本文選取唐山市路南區路網中24條路段的交通流量數據作為實驗數據，該數據的時間間隔為5分鐘。通過計算全局時空相關性ST-ACF和多元鄰接的局部時空相關性MALST-ACF分析在不同時間延遲和空間延遲下道路交通流與其相鄰路段之間的相關性特征。

由于路網的不規整性、不同路段在鄰接路段數量上的差異性，實驗中為了反映各路段的每條相鄰路段之間的影響程度采取行標準化權重矩陣，即用鄰接矩陣中每行的單位元素除以矩陣每行元素總和。

為了能夠準確地描述出唐山市道路網絡交通流相關性的時空變化特征，根據唐山市民的出行規律和全天道路的交通狀態變化特征，本研究將全天數據分為4個時間段：全天（0：00—24：00）、早高峰（7：00—10：00）、平峰（10：00—13：00）、晚高峰（16：00—19：00）。

本文從宏觀和微觀兩個角度出發，分別計算了全局和局部路網在4個不同出行時間段的時空相關性變化特征。

3.1? ? 全局時空相關性分析

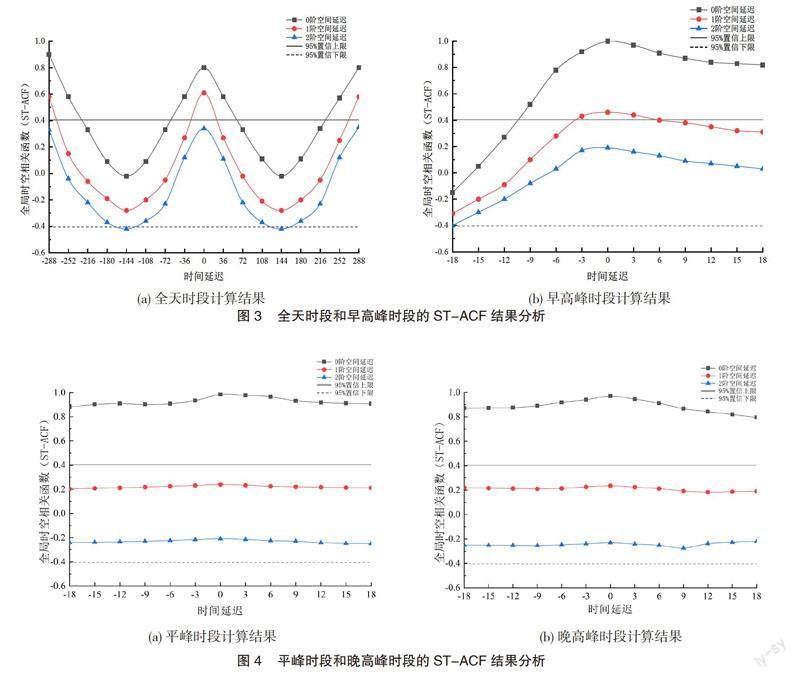
本文采用ST-ACF從整體角度分析全局交通路網在不同時間段的時空相關性系數。由于采取唐山市24條路段，即樣本數量為24，并且采用一元回歸的數學統計方法，計算得到自由度為22，在0.05置信度的條件下顯著性水平臨界值為0.404 39。ST-ACF計算結果在0階、1階、2階和95%置信上、下限的變化特征如圖3、圖4所示。

結合上述4個統計時間段的ST-ACF分析結果，可以得出以下結論。

第一，全局時空相關性系數在一定時間段的分析中具有以天為單位的周期性變化。這一結論說明城市道路交通流之間的變化有規律可尋，為交通擁堵的解決提供一定理論依據，可以利用歷史大數據對未來城市道路的交通流量做預測。

第二，全局時空相關性系數隨著空間鄰接矩陣階數的增加而減小。這說明實驗數據中同一統計時間段的各路段時空相關性隨著距離的增加而逐漸減弱。在空間鄰接矩陣階數為0階和一階時，在一定時間延遲內，當ST-ACF置信上限超過95%時，時空相關性呈現出了顯著正相關；當空間鄰接矩陣階數高于一階時，時空相關性不具備顯著相關性。說明唐山市城市路段在直接相鄰時的時空相關性比較明顯，而對于非直接相鄰的路段表示出時空相關性不顯著的特征。

第三，在各個統計時間段內，不同空間鄰接矩陣下的ST-ACF均呈現出隨單位延遲時間的增加而減小的趨勢。這說明隨著時間延遲的增加城市路段之間的相關性作用在減弱。

3.2? ? 多元鄰接的局部時空相關性分析

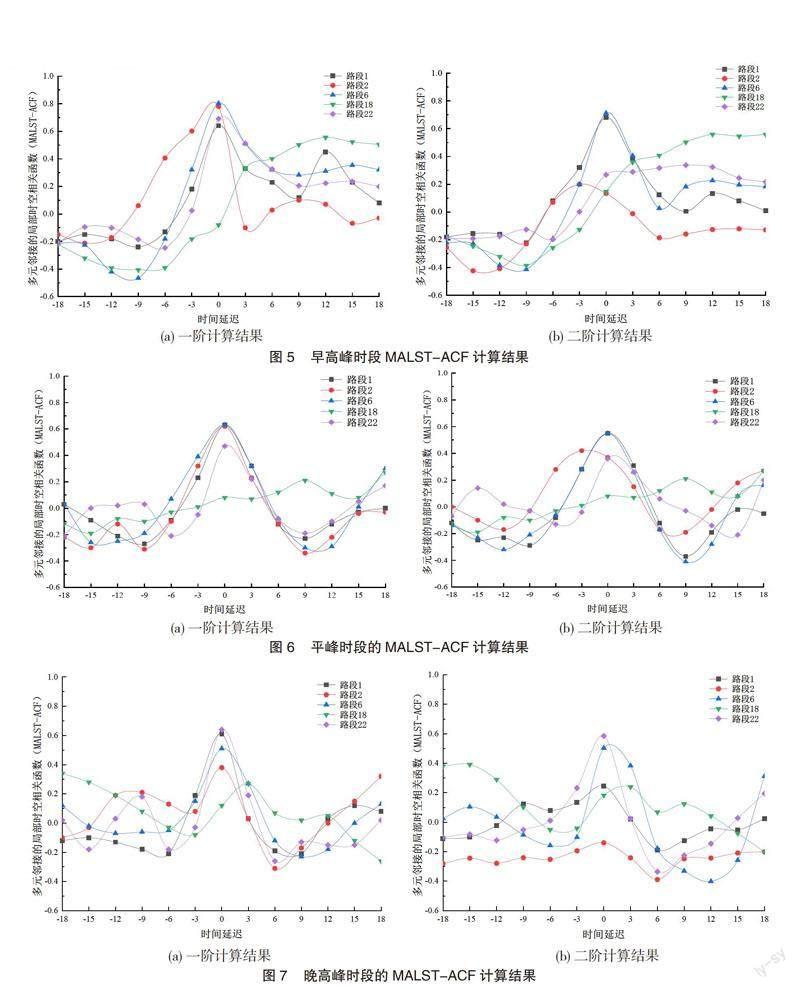
從局部角度出發，由于CCF指數只局限于計算路段上、下游之間的相關性，本文提出了多元鄰接的局部時空相關性函數MALST-ACF來解決多元鄰接的局部時空相關性分析，并分別計算出早高峰（7：00—10：00）、平峰（10：00—13：00）、晚高峰（16：00—19：00）3個統計時間段的局部時空相關性系數如圖5-圖7所示。

從上述3個統計時間段的局部時空相關性系數分析結果來看，可以得到如下結論。

第一，同一延遲時間、不同路段的局部時空相關性系數具有明顯差異，即排除時間因素影響下，固定時間段的單條路段的車流量發生變化時，其鄰接路段的車流量受不同程度的正向或負向反饋。例如圖5中，在時間延遲都為3個單位的情況下，早高峰計算結果中的路段2的時空相關性為負相關，而其他路段的時空相關性為正相關，這表明5條路段之間任意一條路段發生車流量變化時，除路段2的車流量反向變化外，其余路段的車流量均呈正向變化。另外，在同一統計時間段內不同路段的相關性系數變化趨勢也有所不同。例如在晚高峰計算結果中，時間延遲在3個單位內，路段18相關性系數呈現上升趨勢，而其他路段相關性系數均呈現下降趨勢。

第二，同一路段的時空相關性系數MALST-ACF值在不同的統計時間段具有明顯差異，即排除空間影響因素下，固定路段在不同時間段的車流量發生變化時，未來短時間內該路段會呈現正向或負向反饋。例如，綜合圖5、圖6、圖7發現，路段2在早高峰時，在2個時間延遲單位內呈現正相關性，在3個時間延遲單位內呈現負相關性；而路段2在平峰時，在3個時間延遲單位內呈現正相關性，這表明路段2在早高峰車流量發生變化時，不同的時間延遲導致該路段未來時間段的車流量變化趨勢明顯不同，而在平峰時對車流量變化趨勢的影響并不明顯。

第三，通過對局部時空相關性分析發現CCF指數存在只能夠分析路段上、下游關系的局限性，即CCF指數計算只適用于一階鄰接矩陣分析；而本文提出的MALST-ACF分析模型由于引入了空間延遲算子可應用于高階鄰接矩陣分析，因此相對于CCF指數分析其更能全面、準確地描述路網各路段之間的時空相關性。

4? ? 結? ? 論

本文首先構建了空間權重矩陣，計算了路網中各路段之間鄰接關系的權重值；然后基于賦有權重值的空間權重矩陣引入空間延遲算子，通過增加空間延遲算子改進傳統的局部度量指標計算方法，建立了基于多元鄰接的局部時空相關性分析模型，使其適用于復雜城市道路路網的交通流特性研究。最后，本文以唐山市路南區道路路網交通流量作為實驗數據進行分析，實驗結果表明，基于多元鄰接的局部時空相關性分析模型相比傳統局部時空相關性分析模型更有優勢，具體體現在計算二階及以上等高階相鄰路段之間的度量關系時，基于多元鄰接的局部時空相關性分析模型計算所得的路段間的相互影響關系更加準確、全面，能夠為城市交通擁堵的解決以及道路交通流量的預測提供重要的參考依據。

參考文獻：

[1] 陳紹寬，韋偉，毛保華，等．基于改進時空Moran's I指數的道路交通狀態特征分析[J]．物理學報，2013，62（14）：527-533.

[2] 韋偉，毛保華，陳紹寬，等．基于時空自相關的道路交通狀態聚類方法[J]．交通運輸系統工程與信息，2016，16（2）：57-63.

[3] 代偵勇，姜婧，肖明科．基于時空Moran's I指數的全國降雨量自相關分析[J]．華中師范大學學報（自然科學版），2014，48（6）：923-929.

[4] 郭岱．基于大數據的城市交通路況時空分析及可視化系統研究[D]．大連：遼寧師范大學，2017.

[5] 陸百川，李玉蓮，舒芹．基于時空相關性和遺傳小波神經網絡的路網短時交通流預測[J]．重慶理工大學學報（自然科學），2020，34（5）：25-34.

[6] 林廣發，馮學智，江輝仙．時空數據模型建模方法研究[C]．中國地理信息系統協會第八屆年會論文集. [出版者不詳]，2004：818-822.

收稿日期：2023-02-01

作者簡介：陳玉飛（1997—），男，山東臨沂人，工程師，碩士，研究方向：智能交通；黨? ? ?倩（1989—），女，江蘇南京人，高

級工程師，碩士，研究方向：智能交通；陳愛偉（1990—），男，江蘇南京人，工程師，碩士，研究方向：智能交通。

引文格式：陳玉飛，黨倩，陳愛偉．基于 ST-ACF 與 MALST-ACF模型的城市道路時空相關性研究[J]．物流科技，2023，46（2）：10-15，42.