基于最大距離和最大密度的聚類算法改進

白潔 楊懌

關鍵詞：K-Means 算法；聚類分析；聚類中心；最大距離；最大密度

0 引言

最近科學數據收集技術的進步和復雜多樣的數據量的不斷增長，在數據分析或挖掘過程中更難操縱它們或提取有用的信息。此外，為數據找到合適的標簽既昂貴又耗時，因此大多數數據都沒有標簽。這就是無監督聚類方法發揮作用的地方。聚類是將具有相似特征的項目分組在一起的行為。這樣，每個聚類分組由與其他聚類分組的項目不同的相似項目組成。

目前最流行的數據挖掘方法有分類、聚類、關聯規則分析、回歸等，聚類算法是數據挖掘的一個重要分支，它豐富了各種不同的問題主題，在現實生活中有著廣泛的應用，包含機器視覺、信息檢索、圖像處理等領域[1]。它是一種無監督的學習方法，其過程是將數據集劃分成若干個類，使得同一類中的數據信息相似度盡可能大，不同類中的數據信息差異盡可能大[2]。聚類算法近些年不斷發展，現今已經有很多分支，按照算法的性能主要分為基于劃分的聚類、基于層次的聚類、基于網格的聚類、基于密度的聚類等。KMeans算法是基于劃分的聚類算法這一分支中經典的算法。1967年，MacQueen首次提出了K-Means聚類算法[3]。由于它具有實現形式簡單、時間復雜度低的優點，已在數據科學、工業應用等領域中被廣泛采用[4-6]。

1 K-Means 算法及改進

1.1 K-Means 算法

K-Means算法是基于劃分的聚類算法這一分支中經典的算法。K-Means算法一般采用歐氏距離作為度量對象之間相似性的指標。相似度與記錄之間的歐氏距離成反比。記錄之間的相似度越大，距離越小。該算法需要事先指定初始聚類個數k 和初始聚類中心，并根據數據對象與聚類中心的相似度不斷更新聚類中心的位置。當目標函數收斂時，聚類結束[7]。

目前，K-Means算法的改進方法主要集中在以下幾個方向：算法初始k 值的選取、初始聚類中心點的選取、孤立點的檢測與去除。

1.2算法改進

K-Means聚類算法是經典且應用廣泛的基于劃分的聚類方法之一，具有理論可靠、算法簡單、收斂速度快、能有效處理大數據集等優點。但是傳統的KMeans算法過度依賴于初始條件[8]。即初始聚類數目K值和聚類中心的選擇影響最終的聚類結果以及KMeans算法的收斂速度。假設聚類數目K值已經確定，選取不同的初始聚類中心又會導致不同的聚類結果，隨機選取的初始聚類中心點將會增加最終聚類結果的隨機性和不可靠性。在上文的分析中也總結出，K-Means算法對離群點和孤立點敏感。因此針對聚類中心的選擇對K-Means算法作出改進。

在K-Means++中，對于下一個聚類中心點一般選擇距離當次迭代的聚類中心最遠的數據點或者與其最近的數據點，此方法遵循了兩個類簇盡可能遠的原則。因此借鑒K-Means++選擇聚類中心的思想，以及基于密度分類的DBSCAN算法的思路，提出一種優化聚類中心的K-Means算法。改進以及優化聚類中心的選擇與確定，同時基于密度和最大距離來分類的思想也可以避免選擇離群點或孤立點為聚類中心，導致聚類結果有偏差的情況。

傳統K-Means算法是計算各個類內記錄的均值作為新的聚類中心，但往往因為異常值或者離群點導致結果出現局部最優，因此采用最大密度和最大距離的方法來確定聚類中心。基于最大距離和最大密度的中心點初始化方法分為兩個步驟，首先計算所有樣本的密度，然后選取一部分密度較大的樣本作為候選集，然后從候選集中選取彼此相距較遠的k個樣本作為初始中心。

改進后的算法思路是，計算數據集中所有任意兩個數據之間的距離和平均距離，計算出數據的密度和平均密度，設置一個空數據集T，將大于平均密度的所有數據對象添加到數據集T中，選擇密度最大的數據對象作為第一個聚類中心，并將這個數據添加到設置的空數據集F中；再根據定義5計算數據集T中距離數據集F最遠的數據，把這個數據添加到數據集F中；重復計算，直到數據集F中有K 個數據，就是最終的聚類中心。根據距離公式計算其他數據與k 個聚類中心的距離，根據大小劃分到最近的聚類當中。

具體步驟如下：

輸入：n條數據的數據集D，聚類個數k

輸出：k 個聚類中心和k 個類

Step1：根據歐氏距離公式和定義1計算出任意兩條記錄之間的距離和平均距離。

Step2：根據定義3和定義4計算出數據集中每條數據的密度和平均密度。

Step3：比較每條數據的密度和平均密度，設置一個空數據集T，將大于平均密度的數據添加到T中。

Step4：在數據集T中選取密度最大的一條數據作為第一個聚類中心，加入新數據集F中。

Step5：從T中選擇離數據F最遠的數據，作為下一個聚類中心。

Step6：重復step5，直到數據集F中有k條數據，也就是k個聚類中心。

Step7：根據剩余n-k條數據和k個聚類中心之間的距離，依次劃分到相應的類當中，得到k個聚類。

2 實驗結果對比分析

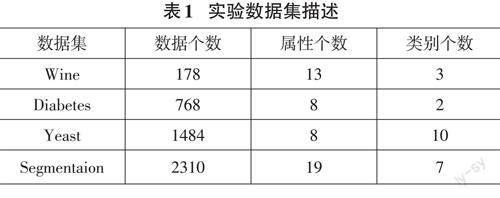
在K-Means++的算法思想基礎上，提出一種基于k 值確定和優化聚類中心的K-Means 算法（DD-Kmeans）。其中，優化聚類中心是基于距離和密度來確定聚類中心，和DBSCAN 算法有部分相同思想。因此，這部分實驗是將改進的K-Means 算法與KMeans++、DBSCAN算法進行對比分析。實驗部分選擇UCI上的機器學習常用數據集，包括wine、yeast、Di?abetes、segmentation。

實驗從準確率和算法穩定性兩方面進行對比。準確率就是改進算法DD-K-means的聚類結果中，每個類別的數量與數據集原始類中數據數量的比值。將DD-K-Means算法與K-Means++算法，DBSCAN算法在wine，segmention，yeast，Diabetes 數據下多次實驗，取平均值。實驗結果圖如圖1所示，由圖可以分析出，DD-K-Means算法相較于K-Means++和DBSCAN有明顯的準確度提升。在wine 數據集上，DD-KMeans算法聚類準確率相較于其他算法提高了7.03%，4.06%；而在Segmentaion 數據集上，DD-KMeans算法相較于其他算法提高了16.54%，13.64%。數據量越大，聚類效果提升更明顯。因此，基于密度和最大距離的算法改進，有效優化了聚類結果。如圖2 所示，DD-K-Means 算法和K-Means++算法，DB?SCAN算法在Yeast數據集上進行多次實驗，明顯看出K-Means++算法穩定性在這三種算法中最差，最高達到19%的差值，而DBSCAN算法近11%的波動范圍。DD-K-Means將算法準確率的波動維持在6%以內，保證了算法的穩定性。

3 結論

K-Means聚類算法中初始聚類中心一般是隨機選取，聚類數目往往人為確定，使得有不同的初始聚類中心和聚類數目的相同數據集聚類結果不一樣。為了解決此問題，基于最大距離和最大密度選取聚類中心，計算數據的距離和平均距離，密度和平均密度，根據距離和密度選擇合適的聚類中心，避免人為選擇聚類中心影響聚類結果，同時也避免孤立點和離散點對聚類結果的影響。實驗結果表明，所提出算法聚類結果更穩定，效果更好。與K-Means聚類算法相比，改進算法具有如下優勢：初始聚類中心以及其他聚類中心的選取是經過計算得到的。但是，由于改進算法同時進行了距離和密度的計算，導致復雜度增加；聚類數目人為確定的問題也沒有改善。因此，在今后的研究工作中，可以考慮優化k值的選擇，利用程序確定合適的k值，同智能優化相結合，以得到更加高效的聚類效果。