高頻焊薄壁管成型仿真與分析*
蔡 緒 明
(中石化石油工程機械有限公司沙市鋼管分公司)
0 引 言
由于優異的管型質量和突出的成本優勢,油氣管道工程用小口徑薄壁鋼管越來越多地選用高頻焊管。但薄壁高頻焊管在成型過程中鋼帶邊緣受力和變形狀態很難控制,成型工藝參數稍有偏差就可能導致鋼帶邊緣出現波浪,影響焊接質量,甚至導致無法正常合縫和焊接。實際生產中多通過鋼管試制來制定和優化生產工藝,既耽誤了生產進度,又造成了材料浪費。目前有研究報道通過建模對傳統的粗成型-精成型排輥成型機組的成型過程進行仿真分析來代替鋼管試制[1-3],并取得了積極進展。中石化石油機械沙市鋼管分公司高頻焊管機組由美國ABBEY公司引進,其先進的粗成型-TBS(過渡梁)成型-精成型工藝與通常的排輥成型技術差別較大,機架間距、數量和成型方式都不一樣,文獻中的仿真軟件技術對該公司的借鑒意義不大。
筆者基于美國ABBEY高頻焊管機組對成型過程進行建模,通過分析不同軋輥的位置變化對鋼帶邊緣變形量的影響,計算鋼帶邊緣變形最佳時的工藝參數用于實際鋼管生產,并通過DL245M ?406.4 mm×6.0 mm高頻焊管的批量生產驗證,取得了較好的效果。
1 模型創建和處理
ABBEY高頻焊管機組的成型一般包括粗成型、TBS成型和精成型3個階段。鋼帶在每個階段都會產生較大的塑性變形,同時與各道次的上下輥和彎邊輥發生滾動摩擦接觸。
1.1 幾何建模
采用ANSYS 幾何建模編輯工具SCDM,按照提供的二維圖進行三維幾何建模。本文采用?219.1、?406.4和?610.0 mm共3種輥型建立高頻焊管成型仿真模型,用D406.4典型輥型進行全流程仿真分析,成型輥組整體裝配示意圖見1。
1.2 材料選擇
材料選用常用的L290鋼帶,規格為1 276 mm×6.0 mm(對應鋼管規格為?406.4 mm×6.0 mm),采用柔性體進行模擬。考慮到鋼帶在成型壓制過程中塑性變形較大,選用雙線性等向強化材料模型來設置鋼帶的材料屬性:屈服強度290 MPa,切線模量為8.60 GPa[4-5]。
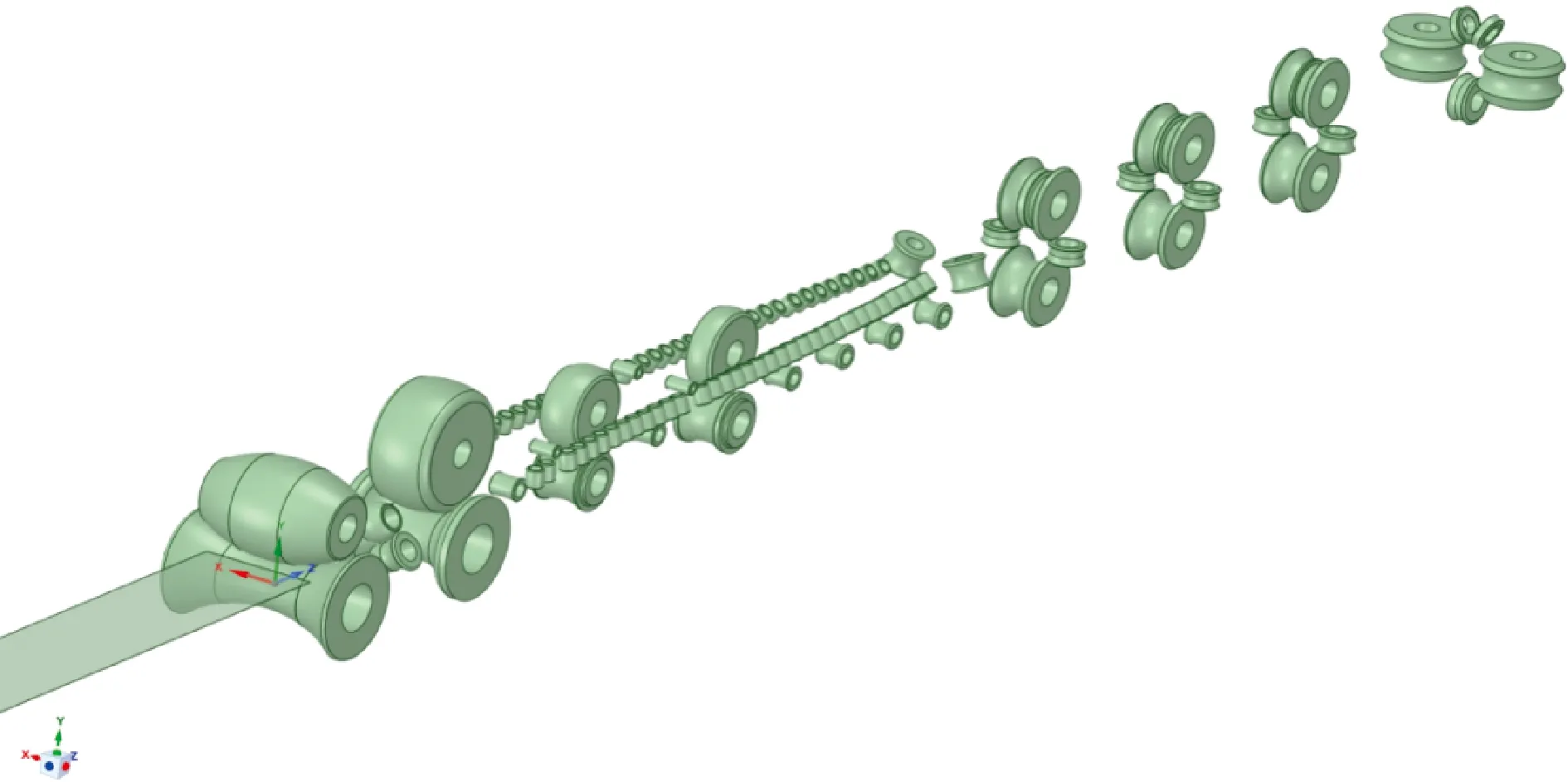
圖1 成型輥組整體裝配示意圖Fig.1 Assembly diagram of the shape-forming roller set
1.3 有限元模型創建
輥組采用高強結構鋼,在分析中視為剛性體,不考慮其彈性變形,采用實體建模[6-9];鋼帶為連續帶狀體,在成型壓制過程中厚度方向的變形量遠小于其他方向,故采用殼體建模[10-12]。將鋼帶建成一個面體,選取24 m長的鋼帶來模擬,讓鋼帶穿過各成型階段。因鋼帶經過各壓輥的過程中呈對稱性形變,分析模型選用的模型量以減少仿真分析的計算量。
1.4 接觸聯接定義
鋼帶與主動輥之間采用有摩擦接觸[13]的方式創建接觸對,設置相應的摩擦因數為0.2,假設動摩擦因數和靜摩擦因數相等。鋼帶與從動輥之間采用無摩擦接觸的方式創建接觸對。通過預定義接觸對,鋼帶在運行過程中與各輥組接觸,接觸部位取決于鋼帶的受力和變形狀態。
2 整體分析與結論
2.1 D406.4規格薄壁管成型過程仿真
以粗成型下輥為基準進行定位,粗成型上輥位置決定輥縫大小。鋼帶厚6.0 mm,設定粗成型1#和2#輥組輥縫為6.2 mm,3#和4#輥組輥縫為6.4 mm。成型分析中設定鋼帶的前進速度為18 m/min,為了避免堆鋼,驅動輥轉速沿著鋼帶前進方向逐漸加快,其線速度如表1 所示。

表1 各驅動輥組線速度Table 1 Linear velocities of driving roller sets
圖2為整個成型段的鋼帶等效塑性應變分布。圖3為精成型段的鋼帶(管坯)的變形局部云圖。可見最大等效塑性變形主要分布在鋼帶邊緣,鋼帶從粗成型開始變形到精成型后成為管坯的過程中,鋼帶邊緣的最大等效塑性變形值一直在升高,最大值達15.54%。在鋼帶端部(管坯截面)截取9個單元進行等效塑性應變和等效應力分析,如圖4所示。圖5和圖6分別為等效塑性應變和等效應力的時間歷程。由圖5和圖6可知,各單元的等效塑性應變在不同成型道次變化率不同,其中A(921428)單元在鋼管底部,塑性應變在第一成型道次(1#輥組)等效塑性應變變化最快,后趨于穩定,對鋼帶邊緣塑性應變影響大的是后面精成型道次。各單元的等效應力呈震蕩態勢,最大應力分布隨著帶鋼和成型輥的接觸而變化,部分接觸部位的等效應力超過鋼帶屈服極限,D(864116)單元壓力峰值甚至超過1 000 MPa。

圖2 整段鋼管等效塑性應變分布Fig.2 Effective plastic strain distribution of the whole steel pipe

圖3 鋼管過精成型段變形局部云圖Fig.3 Local deformation nephogram of steel pipe passing the fine shape-forming stage

圖4 鋼帶端部(管坯截面)9個單元分布圖Fig.4 Distribution of 9 elements at the end of steel strip(pipe cross-section)
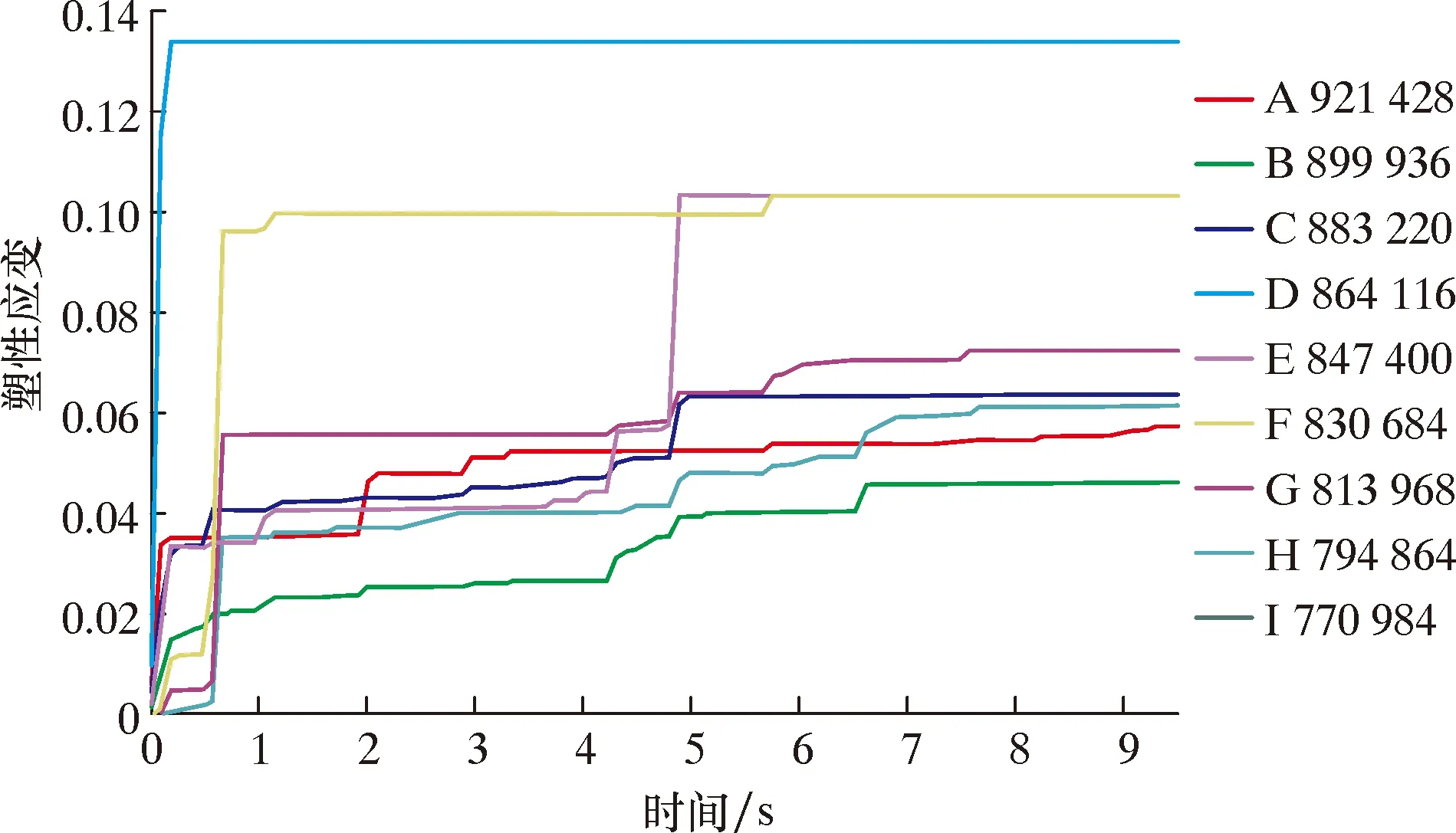
圖5 鋼帶端部各單元在不同成型階段的等效塑性應變時間歷程Fig.5 Variation of effective plastic strain with time for elements at the end of steel strip in different shape-forming stages
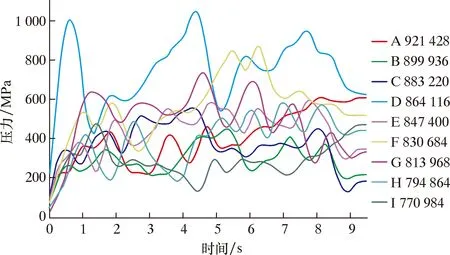
圖6 鋼帶端部各單元在不同成型階段的等效應力時間歷程Fig.6 Variation of effective stress with time for elements at the end of steel strip in different shape-forming stages
在設定件下,仿真模擬顯示成型后的鋼帶邊緣(圖3管縫處)出現了周期性波浪變形,從圖5的I(770984)單元曲線可以計算出鋼帶邊緣波浪主要出現在粗成型段過彎邊輥區域。經過TBS成型輥和精成型輥后,波浪雖有所減小,但仍然會影響焊接質量[14]。仿真模擬的計算結果與相同工藝條件下的實際生產出現的波浪基本一致,證明仿真分析方法可行。
2.2 不同規格管徑薄壁管成型過程仿真模擬
按照2.1方法建立?219.1和?610.0 mm鋼管的仿真模型[15-16],進行整體模擬仿真。仿真模擬計算結果見圖7和圖8。由圖7和圖8可知,鋼管成型過程均出現邊緣波浪,且產生部位同樣集中在粗成型過彎邊輥處。
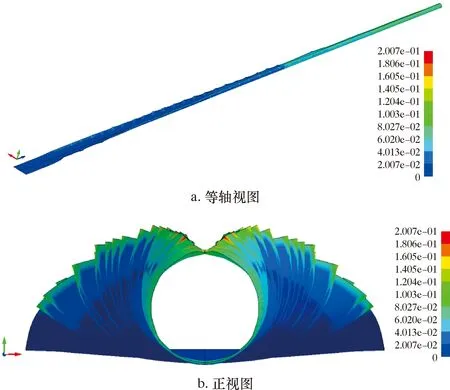
圖7 管徑?219.1 mm過精成型后鋼帶等效塑性應變分布Fig.7 Effective plastic strain distribution of steel strip of ?219.1 mm pipe after fine shape-forming

圖8 管徑?610.0 mm過精成型后鋼帶等效塑性應變分布Fig.8 Effective plastic strain distribution of steel strip of ?610.0 mm pipe after fine shape-forming
3 成型工藝參數影響研究
設定條件下的仿真模擬計算結果顯示,鋼帶在粗成型過彎邊輥處出現邊緣波浪,將嚴重影響高頻焊接質量。采用簡化模型對直徑影響邊緣波浪形成的下山量和彎邊高度進行仿真模擬分析,簡化分析模型如圖9所示,包含1#輥組、1.5#彎邊輥組、2#輥組、鋼帶、托板、壓板,鋼管規格為?219.1 mm×6.4 mm、?406.4 mm×6.2 mm和?610.0 mm×7.0 mm,計算采用鋼帶長度8 000 mm。
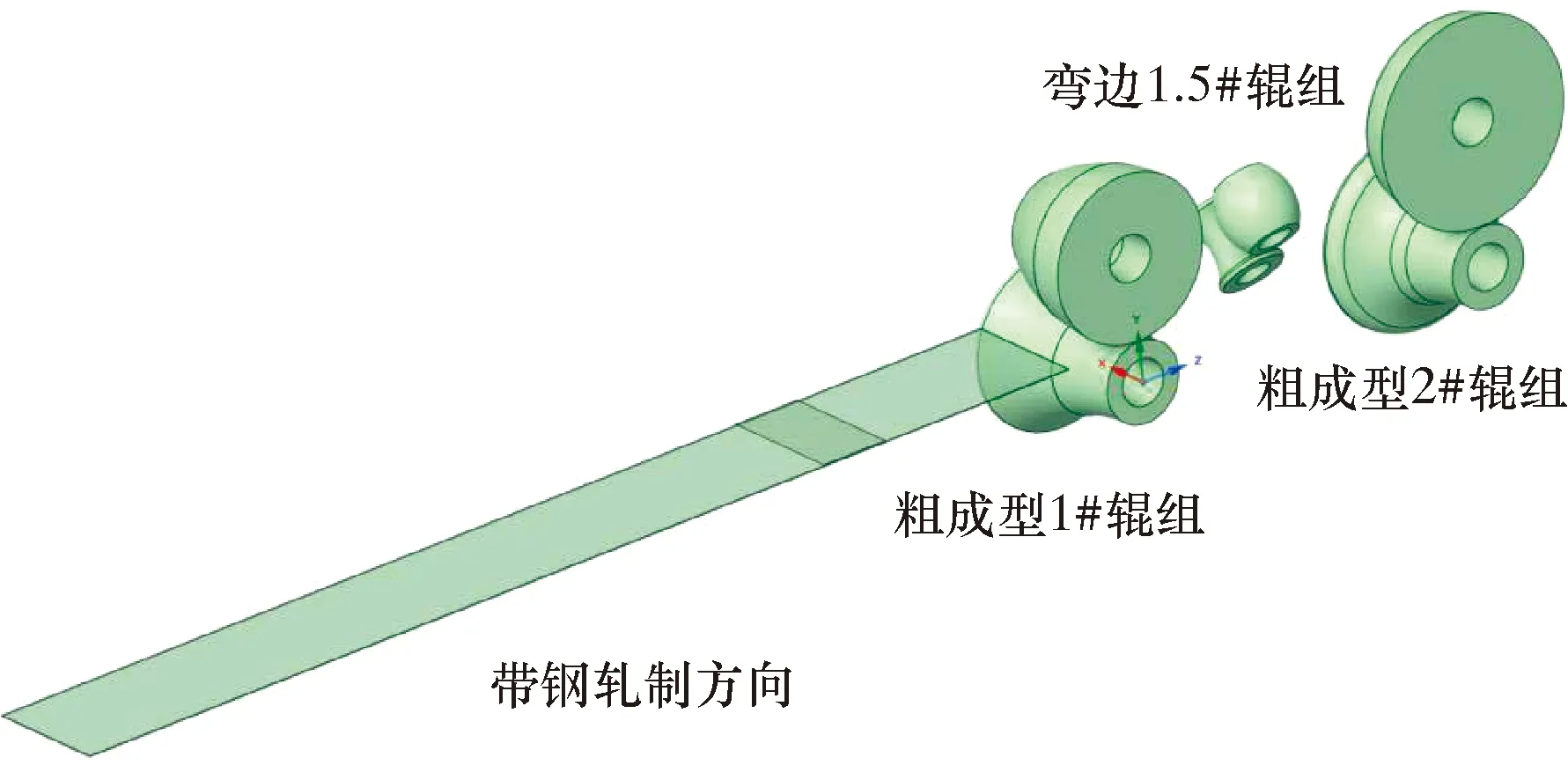
圖9 參數研究簡化分析模型Fig.9 Simplified analysis model of parameters
3.1 下山量
下山量由2#輥組底輥與1#輥組底輥的高度差來表征。除下山量外,其他工藝參數在在仿真模擬過程中保持不變,成型速度采用18 m/min。仿真模擬時將2#輥組的底輥高度相對1#輥組分別下移20、60、100、140和200 mm,進行3種規格鋼管的成型仿真模擬,計算出的鋼帶邊緣徑向變形曲線如圖10所示。
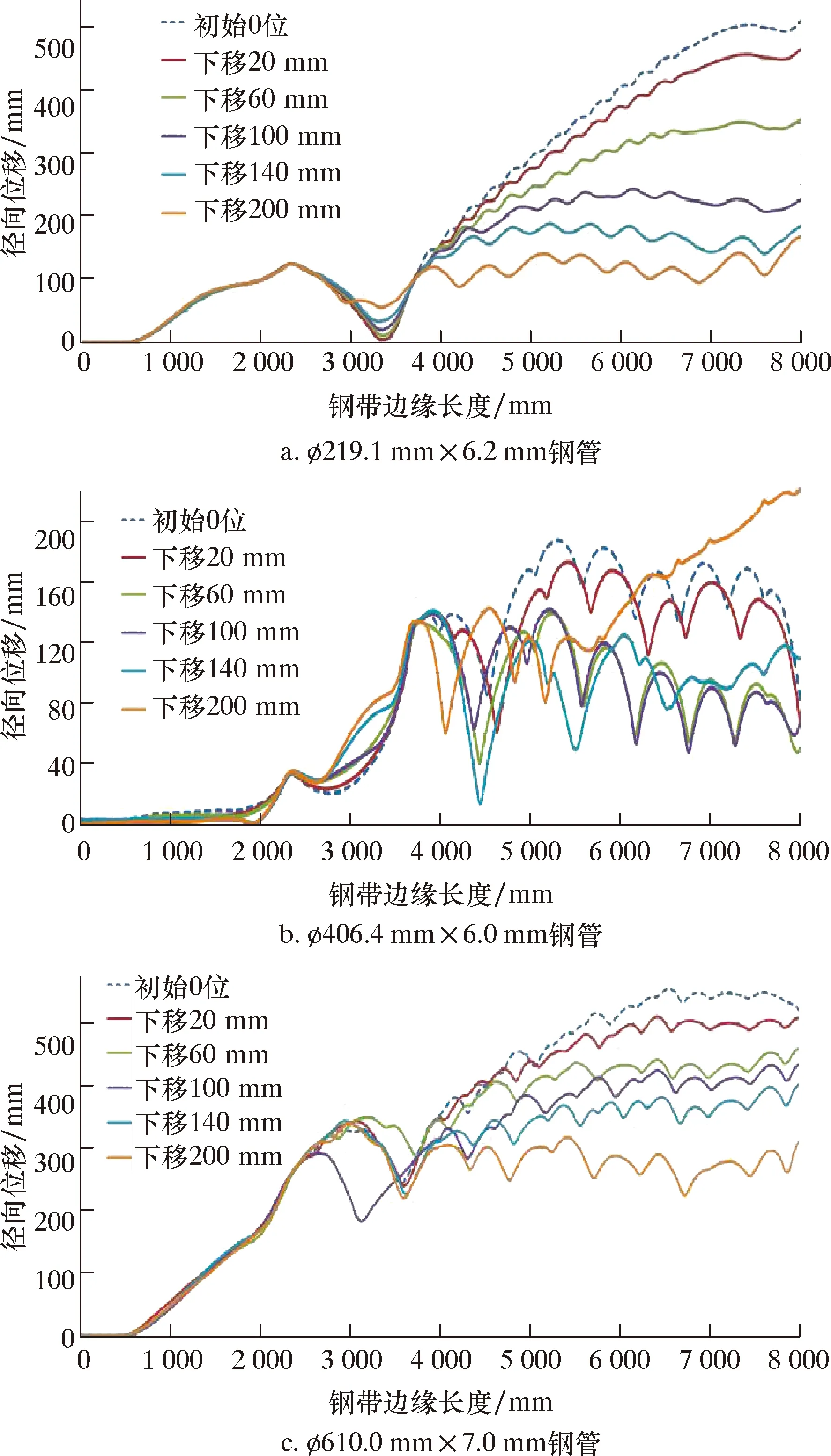
圖10 不同下山量的鋼帶邊緣徑向位移曲線Fig.10 Radial displacement of steel strip edge under different downhill amounts
由圖10可知,所有規格鋼管的鋼帶邊緣徑向位移沿長度方向都有明顯的變化,但其隨下山量的變化趨勢差異較大。對彎邊輥(1.5#輥)至2#輥組的鋼帶(對應于3 800~5 500 mm)邊緣的徑向位移進行線性擬合,擬合曲線見圖11,線性擬合度如表2所示。

表2 不同下山量鋼帶邊緣線性擬合度Table 2 Linear fitting degree of steel strip edge under different downhill amounts
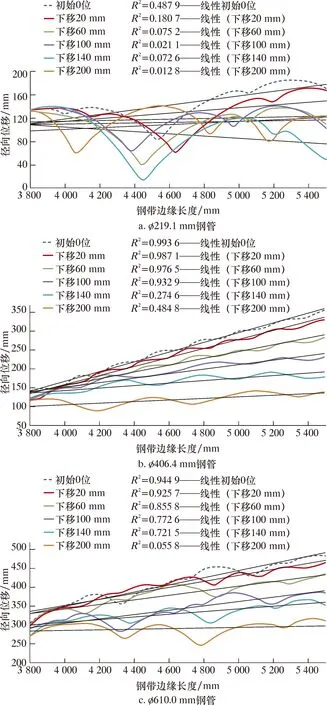
圖11 不同下山量的鋼帶邊緣徑向位移線性擬合Fig.11 Linear fitting of radial displacement of steel strip edge under different downhill amounts
由表2可知,鋼帶邊緣徑向位移的線性擬合度隨著下山量的增加而下降,鋼帶邊緣波浪呈增大趨勢。不同規格鋼管的線性擬合度相差較大,對于?406.4和?610 mm鋼管,可以通過降低下山量來減小鋼帶邊緣波浪的發生趨勢;但對于?219.1 mm鋼管,減小下山量對消除鋼帶邊緣波浪的作用有限。
3.2 彎邊高度對邊浪影響研究
除彎邊輥高度外,其他工藝參數在仿真模擬過程中保持不變,仿真模擬時將彎邊輥高度相對輥花圖定位的初始位置分別上移40、80、120 mm和下移40、80、120 mm,進行進行3種規格鋼管的成型仿真模擬,計算出的鋼帶邊緣徑向變形曲線如圖12所示。
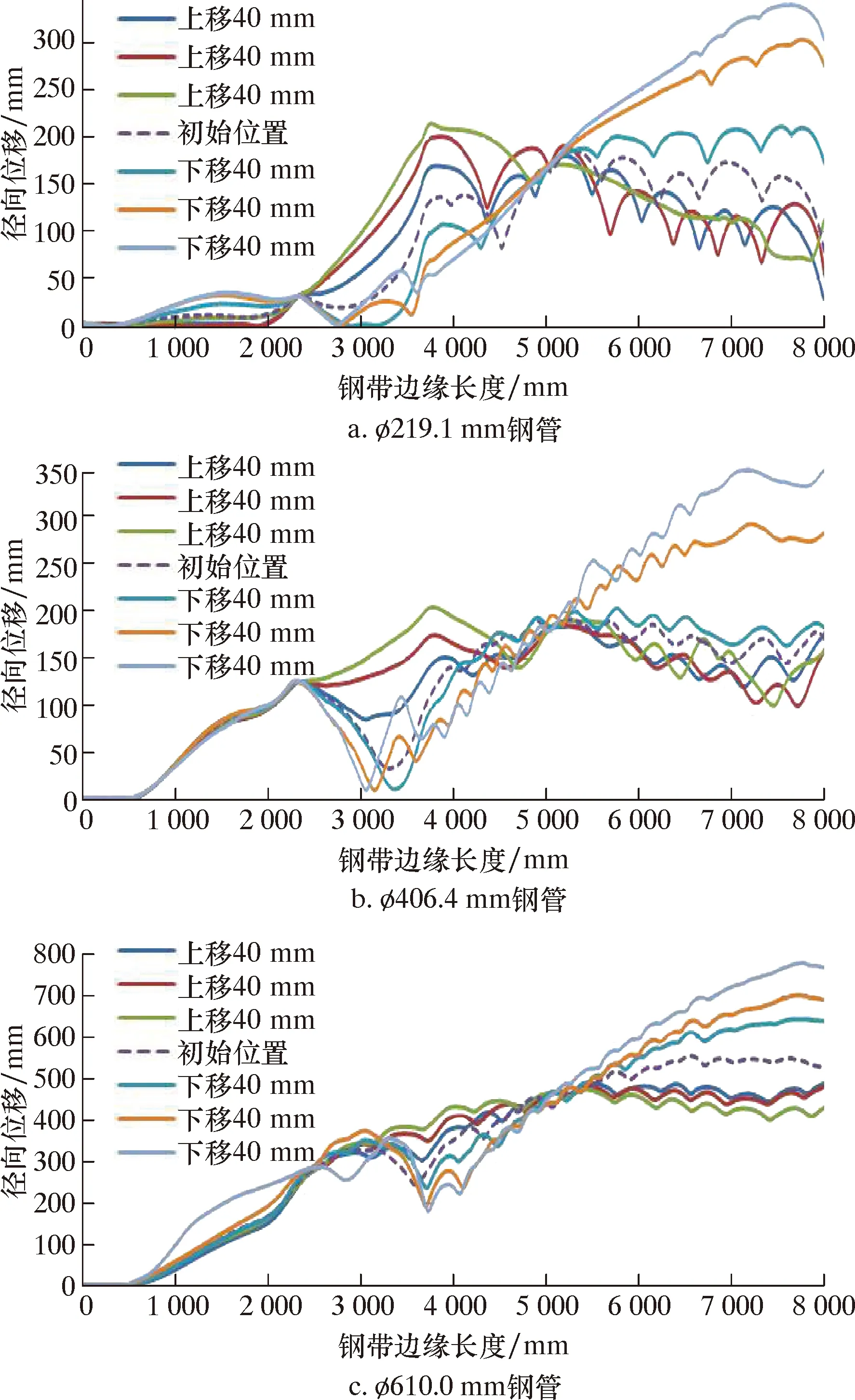
圖12 不同彎邊輥高度的鋼帶邊緣徑向位移曲線Fig.12 Radial displacement of steel strip edge under different edge-bending roller heights
由圖12可知,所有規格鋼管的鋼帶邊緣徑向位移沿長度方向都有明顯的變化,但其隨彎邊輥高度的變化趨勢差異較大。對彎邊輥(1.5#輥)至2#輥組的鋼帶(對應于3 800~5 500 mm)邊緣的徑向位移進行線性擬合,擬合曲線見圖13,線性擬合度如表3所示。

表3 不同彎邊輥高度鋼帶邊緣線性擬合度Table 3 Linear fitting degree of steel strip edge under different edge-bending roller heights
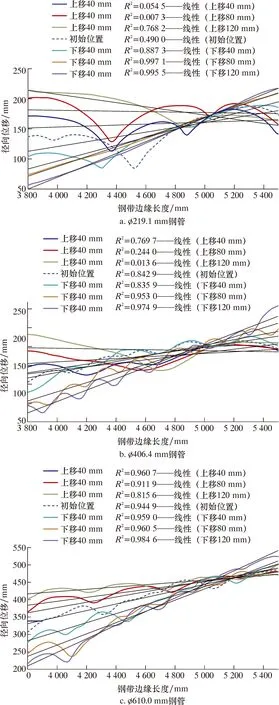
圖13 不同彎邊輥高度的鋼帶邊緣徑向位移線性擬合Fig.13 Linear fitting of radial displacement of steel strip edge under different edge-bending roller heights
由表3可知,鋼帶邊緣徑向位移的線性擬合度隨著彎邊輥下移量的增加而提高,當下移量為80~120 mm時,3種規格鋼管的線性擬合度均超過0.95,鋼帶邊緣趨近平直。但不同規格鋼管的線性擬合度隨彎邊輥高度的變化趨勢明顯不同:?610.0 mm鋼管上移、下移彎邊輥高度均可見證鋼帶邊緣波浪的發生趨勢,而?406.4 mm鋼管宜通過下移彎邊輥高度來減小鋼帶邊緣波浪的發生趨勢;而?219.1 mm鋼管只能通過下移彎邊輥高度來消除鋼帶邊緣波浪。
考慮到彎邊輥下移對降低鋼帶邊緣波浪的積極影響,將彎邊輥高度繼續下移160 mm和下移200 mm,采用以上同樣的模型和邊界條件進行線性擬合,線性擬合度如表4所示。由表4可知,繼續增大彎邊輥下移量將使線性擬合度下降,不利于降低鋼帶邊緣波浪的發生趨勢。
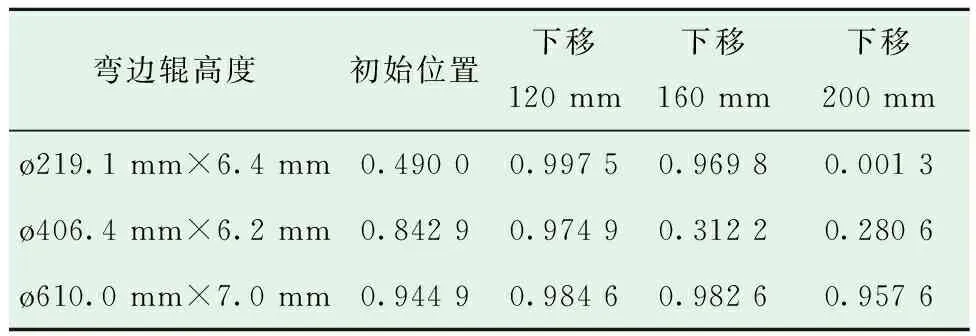
表4 不同彎邊輥高度鋼帶邊緣線性擬合度Table 4 Linear fitting degree of steel strip edge under different edge-bending roller heights
4 應用實例
4.1 技術思路
建立設備三維數字模型,形成相應模型庫。根據軋制管型要求選定配套輥型,將模型進行組裝。組裝時按照輥花圖進行初始定位,得到各輥的初始位置,包括輥的高度、角度等。然后將整體三維模型進行離散,導入LSDYNA軟件中進行成型過程的仿真。計算完成查看鋼管成型質量,重點關注邊緣波浪的大小。通過多種成型工藝參數的匹配方案的仿真計算,確定最佳的成型工藝參數,通過批量生產進行最終驗證。
4.2 實例驗證
2022年5月,在L245M ?406.0 mm×6.2 mm鋼管生產時,利用建模軟件對確定的材料參數和成型工藝參數的匹配方案仿真計算,獲得最佳的工藝參數后,在模型中確定各軋輥的空間位置。通過軟件直接測量模型中各軋輥的相對距離,以粗成型1#輥組下輥為基準,后續輥組下山量如圖14所示。彎邊下輥空間位置數據采用類似方法測出。
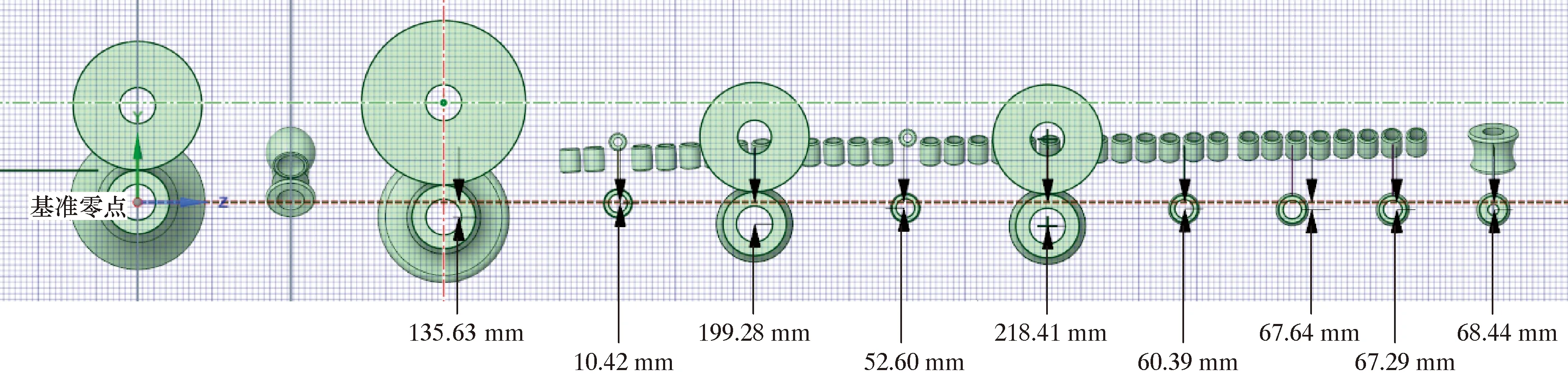
圖14 成型機架輥組下山量Fig.14 Downhill amount of the roller set of the shape-forming machine
根據仿真計算出的最佳成型工藝參數進行設備調型并組織生產,共生產鋼管436 t,既節省了2天的鋼管試制時間,且綜合材耗僅1.063,較平均材耗下降了2%,取得了良好的經濟效益。
5 結 論
(1)LSDYNA軟件適用于高頻焊管的粗成型-TBS成型-精成型過程的仿真分析。
(2)鋼帶邊緣波浪主要出現在高頻焊管的粗成型段過彎邊輥區域。
(3)鋼帶邊緣波浪的發生趨勢隨著下山量的增加而升高,但對于?219.1 mm鋼管,通過減小下山量來降低鋼帶邊緣波浪的作用有限;鋼帶邊緣波浪的發生趨勢隨著彎邊輥下移量的增加而減小,當下移量為80~120 mm時,鋼帶邊緣趨近平直。

