液滴撞擊柔性疏水表面完全反彈的實驗研究

2023-07-12 01:12:52楊磊劉細妙李鐘洪

實驗流體力學 2023年3期

楊磊，劉細妙，李鐘洪

深圳大學土木與交通工程學院，深圳 518060

0 引言

液滴以一定速度撞擊固體表面的動力學行為廣泛存在于自然界和人類活動中，在噴墨打印[1]、噴霧冷卻[2]、飛機防冰設計[3]、農作物種植[4]、病毒飛沫傳播[5]、復合材料3D 打印[6]等領域中都有著重要的意義。

Rioboo 等[7]將液滴撞擊固體表面的動態力學行為劃分為6 種主要形式，分別為鋪展、快速飛濺、冠狀飛濺、逐漸破裂、部分反彈和完全反彈。完全反彈指液滴垂直或以一定角度撞擊固體表面后，以完整的形態從固體表面脫離的現象。影響液滴撞擊固體表面后發生完全反彈的因素眾多，主要包括接觸角[8]、粗糙度[9]、液滴黏性[10]等。Antonini 等[8]發現只有后退接觸角 Rθ＞ 100°時，才能觀察到完全反彈。Bartolo 等[9]發現液滴撞擊疏水粗糙表面時，既可以從基底表面反彈，也可以被牢牢黏附于基底表面。Okumura 等[10]認為黏性系數對液滴反彈行為的影響可以忽略不計。

當液滴撞擊固體表面時，液滴韋伯數（We）過高或過低均無法發生完全反彈，液滴僅在一定韋伯數范圍內才會發生完全反彈。Richard 等[11]觀察到在We ?1的條件下，液滴撞擊超疏水基底材料表面時會發生完全反彈行為，恢復系數接近0.91。Jung 等[12]發現液滴撞擊不同基底時，反彈行為均發生在撞擊速度較低時。Reyssat 等[13]認為液滴發生完全反彈存在撞擊速度下限。Rioboo 等[14]研究了液滴撞擊超疏水基底材料表面的反彈行為，指出液滴發生完全反彈的極限撞擊速度與液滴直徑的平方根成反比。

相比于其他固體表面，液滴在超疏水表面完全反彈較為常見，而液滴在疏水表面難以發生完全反彈。近年來的研究發現，在適當的條件下，液滴撞擊柔性疏水表面也可以發生完全反彈。Chen 等[15-17]在低韋伯數（We ＜3.4）下系統研究了液滴撞擊黏彈性表面發生完全反彈的物理機制，并給出了液滴發生完全反彈的臨界條件。Lee 等[18]發現可以使用后退接觸角 Rθ預測液滴撞擊瀝青基材的反彈行為。

綜上所述，近年來國內外學者針對液滴撞擊固體表面的完全反彈現象進行了一定的研究，但關于液滴發生完全反彈的韋伯數范圍的實驗結果較為匱乏，且對液滴撞擊柔性疏水材料表面發生完全反彈的影響因素尚缺乏系統的研究和分析。為進一步研究液滴撞擊柔性疏水材料表面的完全反彈行為，本文選用不同彈性模量的柔性疏水材料—聚二甲基硅氧烷（Polydimethylsiloxane,PDMS）和不同黏性的液滴，采用實驗和理論分析的手段，系統地研究液滴黏性和柔性疏水材料彈性模量對液滴完全反彈的影響，進一步揭示液滴在柔性疏水材料表面發生反彈行為的內在機理。

1 實驗樣品及裝置

1.1 實驗樣品

PDMS 以美國道康寧公司（Dowcorning）生產的PDMS 預聚物和固化劑制成，使用了4 種質量配比（10∶1、20∶1、30∶1 和40∶1）的預聚物和固化劑。將充分混合的PDMS 混合物放入真空環境中靜置40 min，待氣泡完全排除后，將其敷設于邊長50 mm、厚2 mm 的正方形玻璃片表面，使用Samkoon SC-100 型勻膠機以800 r/min 的轉速甩膠30 s，再放入125 ℃恒溫箱中，加熱40 min 后取出并自然冷卻，即可獲得厚度約0.13 mm 的PDMS 樣品。利用流變儀（MCR 102 MultiDrive）對PDMS 樣品的剪切彈性模量進行測試，結果如表1 和圖1 所示，其中，G′表示儲能模量，G"表示耗能模量，ω 表示角速度。

表1 PDMS 樣品力學參數（ω=1 rad/s）Table 1 Elastic modulus of PDMS（ω=1 rad/s）

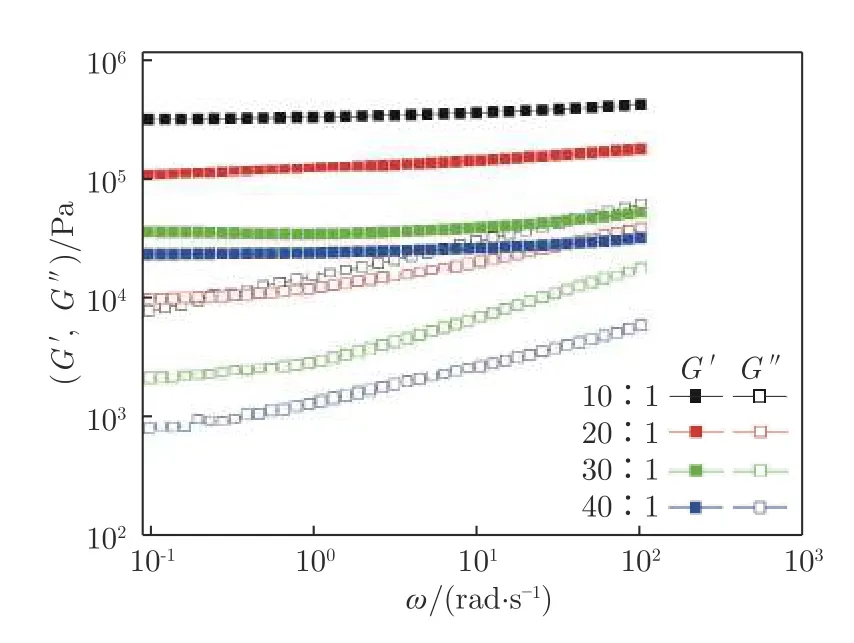
圖1 儲能模量和耗能模量實驗曲線Fig.1 Curves for frequency dependence of storage modulus and loss modulus

實驗選用黏性系數差別較大的3 種液體：去離子水（DI Water）、30%質量比甘油與去離子水的混合溶液（Mix-1）和60%質量比甘油與去離子水的混合溶液（Mix-2）。3 種液體的表面張力系數γ和密度ρ基本相同，黏性系數 μ相差較大。實驗液滴的基本參數如表2 所示。

表2 實驗液滴的基本參數Table 2 Parameters of liquid droplets

1.2 實驗裝置

實驗裝置如圖2 所示。通過微量注射泵控制液體以恒定的流量在針尖處形成液滴并逐漸增大，當液滴自重超過針尖處的表面張力時（液滴直徑為1.98 ± 0.12 mm），液滴脫離針尖自由下落，并以一定初速度垂直撞擊水平放置在正下方的PDMS 表面。通過調節針尖與PDMS 表面的垂直距離可獲得不同撞擊速度和韋伯數。使用Photron SA-X2 高速攝影機記錄液滴撞擊PDMS 表面的全過程，采樣速率為20 000 幀/s，圖像分辨率為512 像素 × 1 024 像素，快門速度1/266 666 s。實驗溫度為22 ± 2 ℃。

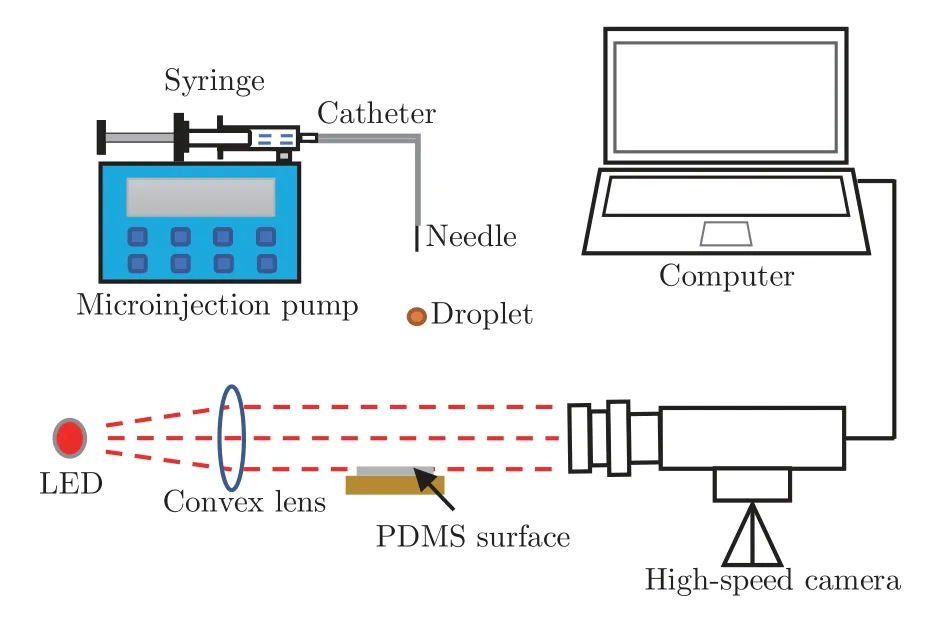
圖2 實驗裝置示意圖Fig.2 Sketch of the experimental setup

采用自行編寫的Matlab 程序對高速攝影照片進行圖像識別和數據分析。將照片進行0-1 二值化處理，確定液滴邊界；合理假定液滴外形軸對稱，對液滴圖像逐行掃描并積分，獲得液滴的體積和質心；采用液滴質心的垂直高度函數進行等時間步的差分，獲得液滴的質心速度，并基于以上參數計算液滴的韋伯數：

式中：D0、v0分別為液滴直徑和質心速度。

2 實驗結果分析

2.1 完全反彈的實驗現象

圖3 為典型的液滴垂直撞擊PDMS 表面并發生完全反彈的高速攝影照片。實驗液體為去離子水，柔性疏水材料為30∶1 PDMS。

圖3 液滴撞擊PDMS 表面的完全反彈行為Fig.3 Droplets rebound completely on a PDMS surface

液滴脫離針尖后，在重力作用下加速下落。液滴撞擊PDMS 表面前近似為圓球狀（圖3（b），定義此時刻為0 ms）。液滴前端（下方）的空氣中存在一個壓力相對較高的動壓區，導致液滴前端形貌發生了一定變化（向內凹陷）；當液滴前端與PDMS 表面接觸時，在液滴撞擊力作用下，彈性模量較低的PDMS 也會發生微小變形。上述2 個原因共同導致凹陷區域內存留的空氣無法及時排出，被包裹在液滴與PDMS 之間，形成空氣薄層[17]（圖3（d））。同時，液滴后端（上方）在慣性作用下繼續向下運動[19]，液滴中心形成空腔，直至液滴后端豎向速度減小為0，空腔停止向下擴展。4.05 ms 時（圖3（e）），液滴達到最大鋪展直徑，空腔擴展至最大，此時空腔與空氣薄層仍未連通，包裹在液滴與PDMS 之間的空氣無法通過中心空腔排出，空氣薄層仍保持完整。達到最大鋪展直徑后，液滴在表面張力作用下加速向中心收縮，在中心位置匯聚后向上運動，與PDMS 表面分離，發生完全反彈（圖3（f）～（i））。

研究發現，當液滴撞擊PDMS 表面時，液滴與PDMS 之間穩定存在的空氣薄層是液滴發生完全反彈的主要原因。空氣薄層阻礙了液滴與柔性疏水材料的接觸，降低了液滴的表面能[16]，使得液滴撞擊過程所消耗的能量減少。如果在液滴撞擊過程中空氣薄層的完整性未被破壞[17]，則液滴發生完全反彈；否則液滴無法發生完全反彈。

2.2 完全反彈韋伯數

圖4 為3 種液滴分別撞擊4 種PDMS 表面后發生完全反彈的最大和最小韋伯數。3 種液滴的表面張力系數和密度基本相等，而黏性系數差別較大，此處僅考慮液體黏性系數和PDMS 彈性模量對完全反彈韋伯數的影響。

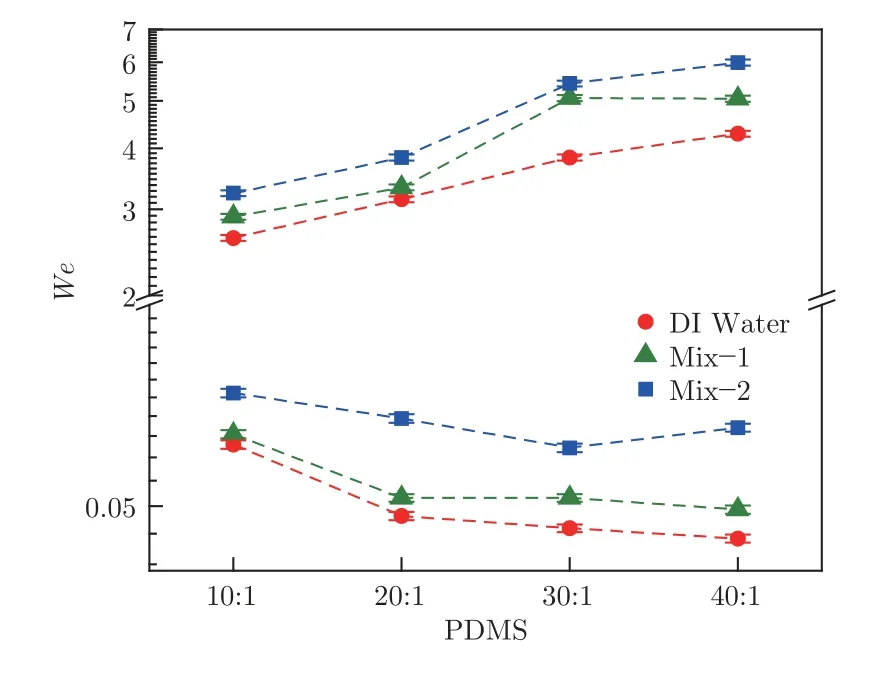
圖4 3 種液滴撞擊4 種PDMS 表面的完全反彈韋伯數區間Fig.4 Weber number range of three droplets rebound on four PDMS surfaces

2.2.1 液滴黏性對反彈韋伯數的影響

由圖4 可以看出，隨著液滴黏性增大，液滴撞擊PDMS 表面發生完全反彈的最大和最小韋伯數均逐漸增大。

由2.1 節分析可知，液滴與PDMS 間空氣薄層的存在是液滴發生完全反彈的主要原因，而液滴撞擊固體表面前的動壓是形成空氣薄層[16]的關鍵因素。動壓導致液滴前端和PDMS 表面發生變形，變形后的表面包裹住固液界面間的空氣，從而形成空氣薄層。若撞擊過程中空氣薄層完好，則液滴發生完全反彈[17]。液滴黏性系數增大會阻礙液滴前端變形，不利于液滴前端凹陷的形成；黏性系數越大的液滴需要越高的撞擊速度以產生更高動壓，才能使液滴前端發生足夠變形，并在液滴與PDMS 表面之間形成空氣薄層。因此，隨著液滴黏性增大，液滴撞擊PDMS 表面發生完全反彈的最小韋伯數逐漸增大。

同樣，液滴的黏性力也會阻礙撞擊處液滴中心空腔的形成與擴展。若空腔向下貫穿到足夠深度，與空氣薄層匯合并破壞其完整性，液滴將無法發生完全反彈。黏性系數較大的液滴需要更高的撞擊速度才能形成貫穿空腔，以破壞液滴前端與PDMS 表面之間的空氣薄層[17]。因此，隨著液滴黏性增大，液滴撞擊PDMS 表面發生完全反彈的最大韋伯數也隨之增大。

2.2.2 PDMS 彈性模量對反彈韋伯數的影響

由圖4 可以看出，隨著PDMS 彈性模量的降低，液滴反彈的最大韋伯數逐漸增大、最小韋伯數逐漸減小，即PDMS 的彈性模量越低，液滴發生完全反彈的韋伯數范圍就越大，這與Chen 等[15]的研究結果一致。

PDMS 彈性模量主要通過PDMS 變形來影響液滴的反彈。撞擊中心點的PDMS 變形最大，以撞擊中心點為中心，PDMS 變形以軸對稱的方式由中心向邊緣逐漸減小。液滴撞擊PDMS 表面時，固液界面間形成的較高壓力的空氣薄層擠壓PDMS，PDMS 彈性模量越低（即越“柔軟”），撞擊點產生的凹陷變形越大，凹陷處的空氣越容易被液滴包裹形成空氣薄層，完全反彈也越容易發生。反之，PDMS彈性模量越高，形成空氣薄層所需要的動壓越高。因此，液滴撞擊PDMS 的最小反彈韋伯數隨PDMS彈性模量降低而減小，即越“柔軟”的PDMS 越容易發生完全反彈。

在鋪展階段，液滴在慣性力作用下有向下運動的趨勢，液滴向四周鋪展，鋪展半徑越來越大，固液界面的空氣薄層在液滴和PDMS 的擠壓下也變得越來越薄，分子力引起的不穩定性[20]使得空氣薄層最終發生失穩破裂。空氣薄層具有較強的變形能力，PDMS 表面彈性模量越低，空氣薄層越厚，越難被破壞，因此液滴發生完全反彈的最大韋伯數越高。

圖5 為最大反彈韋伯數下液滴撞擊PDMS 表面的界面演化過程。由圖5（a）可以看出，在黏性系數較大的液滴（Mix-2）撞擊彈性模量較高（即較為“堅硬”）的PDMS 表面（10∶1 PDMS）發生完全反彈的過程中，黏性力阻礙了液滴中心空腔的形成及液滴前端的變形，同時“堅硬”PDMS 撞擊點產生的凹陷變形小，固液界面間的空氣薄層較薄。若繼續增大液滴的韋伯數，則液滴撞擊速度增大，后端將形成空腔。雖然液滴前端的動壓有利于其自身和PDMS 發生變形并形成空氣薄層[16]，但空氣薄層會在鋪展半徑不斷增大的情況下失去穩定性[20]而發生破裂，使液滴無法發生完全反彈。圖5（b）為黏性系數較小的液滴（DI Water）撞擊彈性模量較低的PDMS 表面（40∶1 PDMS），固液界面間的空氣薄層較厚，即使鋪展半徑較大，空氣薄層也難以發生失穩破壞。但若進一步增大液滴韋伯數，中心空腔將貫穿液滴，導致空氣薄層中的氣體逸出，從而破壞空氣薄層，液滴將無法發生完全反彈[17]。

圖5 最大反彈韋伯數下液滴撞擊PDMS 表面Fig.5 Droplets impact on PDMS surfaces under maximum rebound Weber number

2.3 反彈恢復系數

在液滴撞擊柔性疏水材料表面并發生完全反彈的過程中，由于液滴內部黏性力及柔性疏水材料黏彈性變形的存在，液滴內部的能量消耗體現在液滴完全反彈前后速度的變化。定義液滴發生完全反彈的恢復系數ε為：

式中：v0為液滴自上而下撞擊柔性疏水材料表面時的瞬時質心速度，vr為液滴發生完全反彈并脫離柔性疏水材料表面時的瞬時質心速度。ε始終小于1。

2.3.1 液滴黏性對恢復系數的影響

圖6 為3 種液滴分別撞擊4 種PDMS 表面的反彈恢復系數隨液滴韋伯數的變化曲線。可以看出，在韋伯數相同的條件下，液滴的黏性系數越大，恢復系數越小。

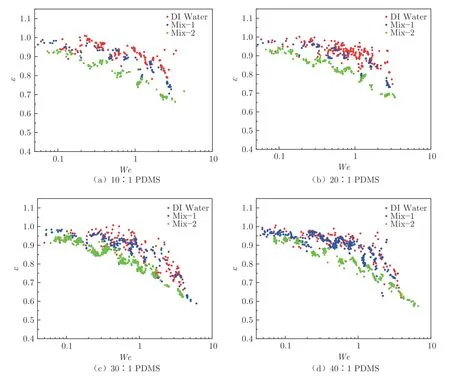
圖6 3 種液滴撞擊不同PDMS 表面發生完全反彈的恢復系數與韋伯數關系Fig.6 Weber number and recovery coefficient of three droplets rebound completely on different PDMS

從液滴接觸至脫離柔性疏水材料表面的整個過程中，液滴的鋪展和收縮受到重力、黏性力、表面張力等的共同影響。重力勢能在撞擊前后的變化基本為0，建立液滴撞擊柔性疏水材料表面過程的能量守恒方程為：

其中，等式左側為液滴接觸柔性疏水材料表面時刻的系統初始總能量，Ek、Es分別為撞擊時刻液滴的動能和表面能；等式右側為液滴脫離柔性疏水材料表面時刻的系統總能量，Ek′、Es′分別為脫離時刻液滴的動能和表面能，Eμ為液滴內部的黏性能量耗散。代入 Ek、Es、Ek′的具體表達形式，則式（3）可表示為：

由于3 種液體的密度和表面張力系數等參數近似相等，因此對于初始撞擊速度 v0和直徑 D0基本相同的3 種液滴，式（4）等號左側的數值大小基本相等。圖7 為具有相同初始撞擊速度 v0和直徑 D0的3 種液滴分別撞擊40∶1 PDMS 表面的高速攝影照片。通過圖像對比可以看出：3 種液滴發生完全反彈脫離PDMS 表面時的幾何外形基本相同，可以認為液滴完全反彈脫離PDMS 表面瞬間的表面能 Es′基本相同。

圖7 3 種液滴撞擊40:1 PDMS 表面Fig.7 Three different droplets impact on 40:1 PDMS

綜上，在初始撞擊速度 v0和直徑 D0基本相同的條件下，液滴發生完全反彈并脫離PDMS 表面的瞬時動能主要受液滴內部黏性能量耗散 Eμ影響。從圖7 可以看出，不同黏性液滴以相近韋伯數撞擊PDMS 表面后的最大鋪展系數基本相同，可以認為液滴在鋪展和收縮過程中的內部速度分布基本相同。液滴黏性系數越大，黏性能量耗散越大。根據式（4）可知，液滴內部的黏性能量耗散增大，將會減小液滴發生反彈脫離PDMS 表面時的動能，導致恢復系數降低。因此，液滴在相同韋伯數下的反彈恢復系數隨黏性系數增大而逐漸減小。

2.3.2 PDMS 彈性模量對恢復系數的影響

圖8 為3 種液滴分別撞擊4 種PDMS 表面發生完全反彈的恢復系數隨韋伯數的變化。

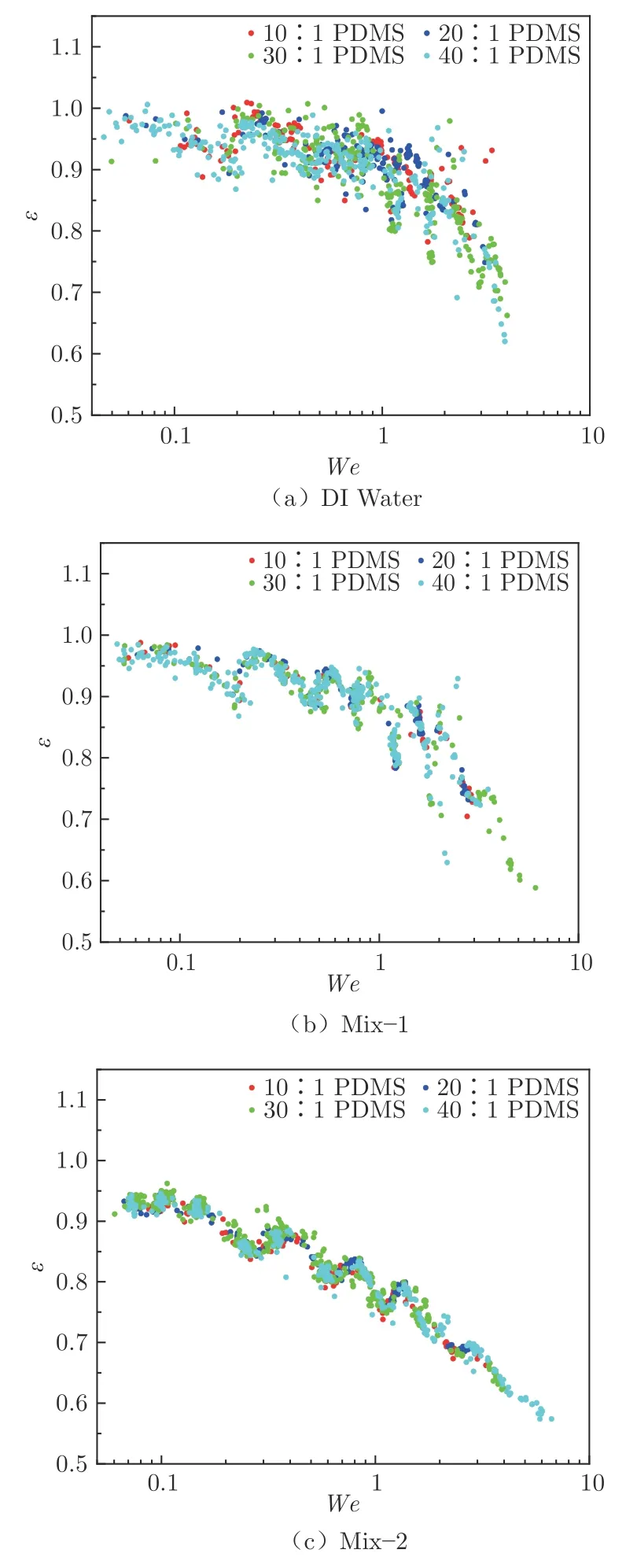
圖8 液滴撞擊4 種PDMS 表面發生完全反彈的恢復系數與韋伯數關系Fig.8 Weber number and recovery coefficient of different droplets rebound completely on four PDMS

圖9 為韋伯數相近的DI Water 分別撞擊4 種PDMS 表面發生完全反彈過程中達到最大水平鋪展時的實驗圖像。可以看出，相近韋伯數下液滴撞擊不同PDMS 表面的演化過程基本一致，PDMS 彈性模量對液滴反彈恢復系數的影響不明顯。隨韋伯數增大，液滴反彈恢復系數以小范圍振蕩的方式逐漸減小。液滴黏性系數越低，反彈恢復系數的離散性越明顯。該現象的原因尚待進一步研究。