面向不完備單值中智信息的三支決策模型①
楊海龍, 任歡歡
陜西師范大學 數學與統計學院,西安 710119
三支決策[1-3]是處理決策問題的一個有效方法, 其核心思想是將一個論域劃分為三個兩兩不相交的部分, 對每個部分制定相應的策略, 以及對三分和策略進行評價.三支決策的模型和理論已經被廣泛研究并應用到了眾多領域.
單值中智集[4]作為直覺模糊集[5]的推廣, 能有效描述不確定性[6-10].單值中智集與三支決策的融合也被廣泛研究[11-19].然而, 如何建立基于不完備單值中智信息系統的三支決策模型, 尚未有文獻涉及.
本文針對不完備單值中智信息系統.首先, 利用平均值法將不完備單值中智信息系統補全為完備單值中智信息系統; 然后, 基于補全的完備單值中智信息系統建立三支決策模型; 最后, 通過選擇產品供應商的例子闡述新模型的應用, 并詳細分析了模型中參數變化對決策結果的影響.
1 預備知識
本節給出所需的一些基本概念.
1.1 單值中智集與單值中智數
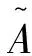
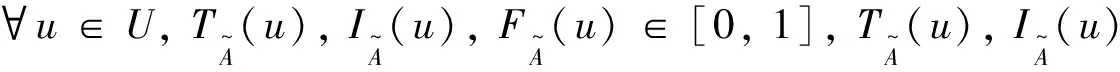
定義2[10]設p,q為兩個單值中智數,k是一個大于0的實數, 定義下面兩個運算:
1)p⊕q=〈Tp+Tq-Tp·Tq,Ip·Iq,Fp·Fq〉;
2)kp=〈1-(1-Tp)k,(Ip)k,(Fp)k〉.
文獻[9]指出了單值中智數排序方法的不足, 并給出了單值中智數的一個新排序方法.
定義3[9]設p=(Tp,Ip,Fp)和q=(Tq,Iq,Fq)是兩個單值中智數,
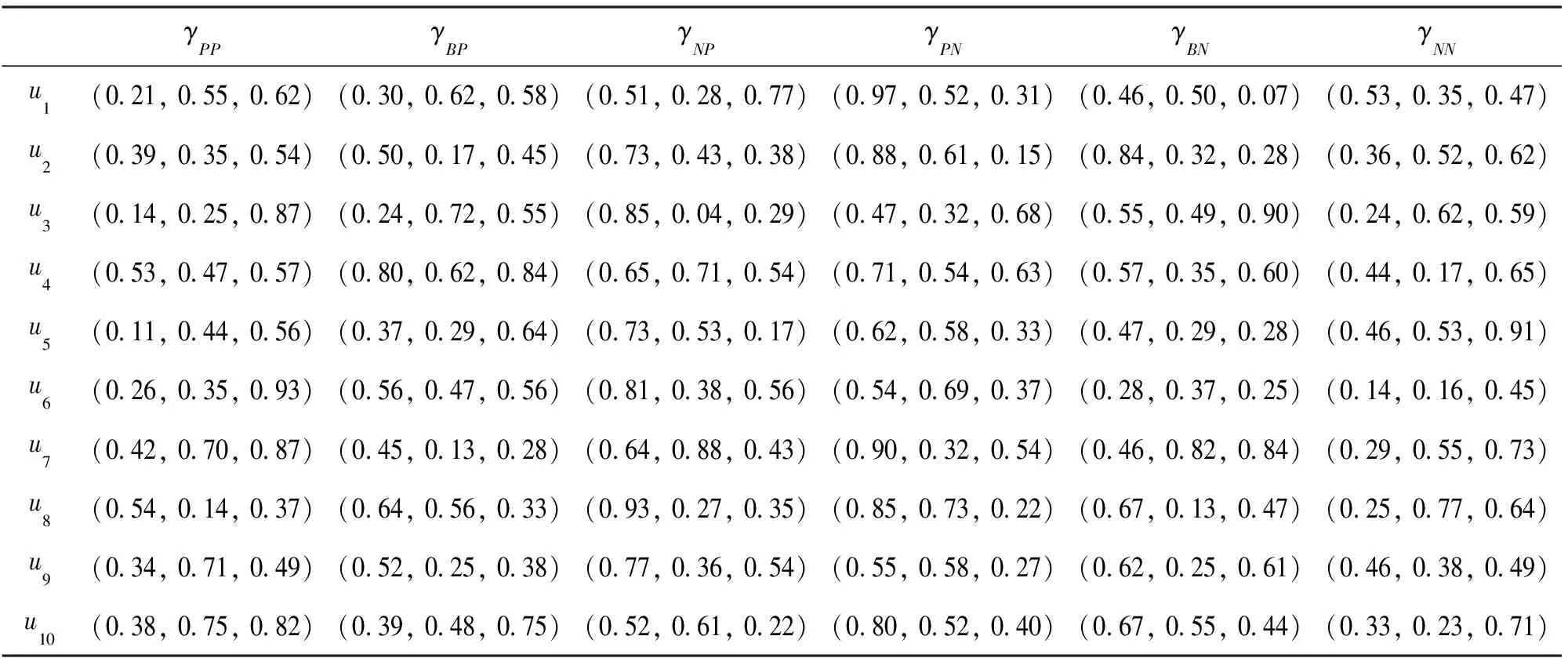
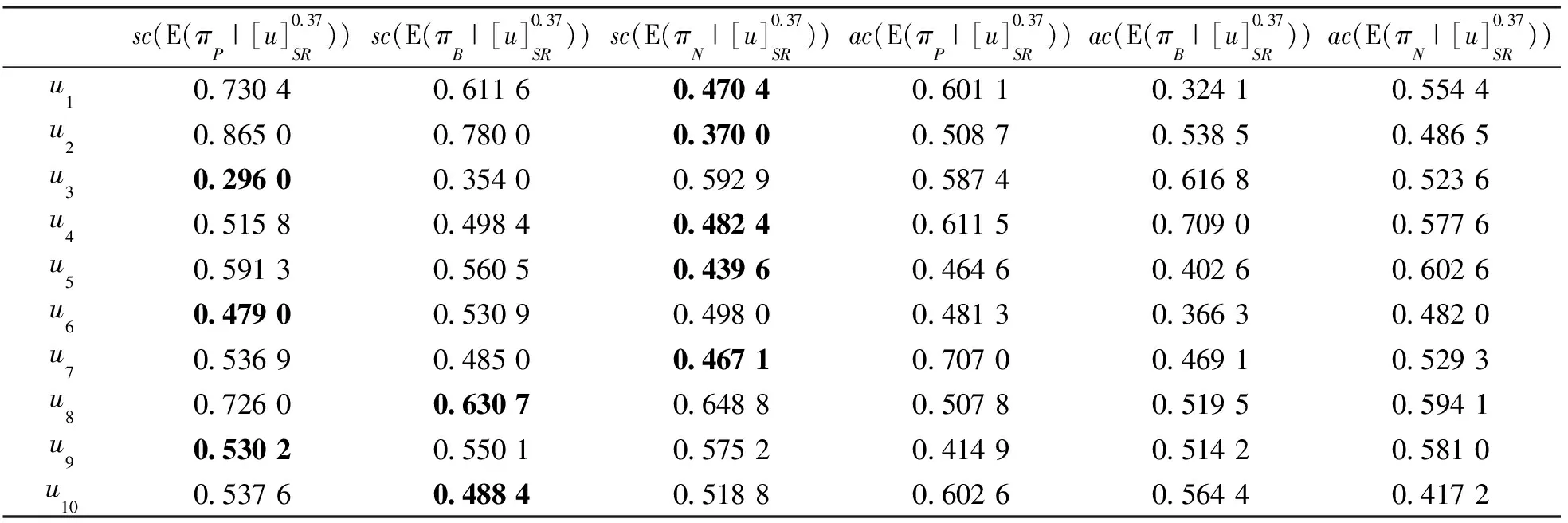
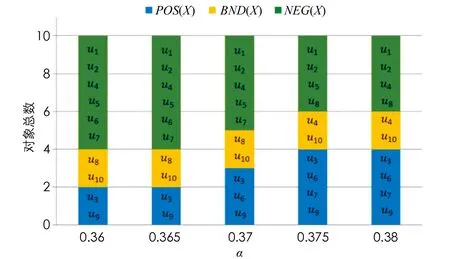
1)若sc(p) 2)若sc(p)=sc(q),ac(p) 3)若sc(p)=sc(q),ac(p)=ac(q),Ip 4)若sc(p)=sc(q),ac(p)=ac(q),Ip=Iq, 則稱p等于q, 記作p=q, 文獻[9]證明了定義3中給出的排序方法可以比較任意兩個單值中智數. 文獻[1]基于貝葉斯決策理論闡述了三支決策的過程.設U為非空有限集,R是U上的一個等價關系,[u]R={v∈U|(u,v)∈R}是u的等價類.設Ψ={C,C}是狀態集,Λ={πP,πB,πN}是行動集, 其中狀態C和C分別表示對象屬于C和不屬于C,πP,πB,πN分別表示對u采取的3個行動, 即決定u∈POS(C),u∈BND(C),u∈NEG(C).損失函數是采取某種行動帶來的損失, 具體如表1所示. 表1 損失函數 在表1中,γPP,γBP和γNP分別表示當對象u屬于C時, 采取πP,πB和πN這3種行為帶來的損失;γPN,γBN和γNN分別表示當對象u不屬于C時, 采取πP,πB和πN這3種行為帶來的損失, 應滿足條件γPP≤γBPγNP,γPN≤γBNγNN.對每個對象采取3種不同行動的期望損失分別為: E(πP|[u]R)=γPPP(C|[u]R)+γPNP(C|[u]R); E(πB|[u]R)=γBPP(C|[u]R)+γBNP(C|[u]R); E(πN|[u]R)=γNPP(C|[u]R)+γNNP(C|[u]R) 其中P(C|[u]R)和P(C|[u]R)分別表示等價類[u]R中的對象屬于C和不屬于C的條件概率. 根據最小風險貝葉斯決策理論, 得到如下決策規則: (P)若E(πP|[u]R)≤E(πB|[u]R), 且E(πP|[u]R)≤E(πN|[u]R), 則u∈POS(C); (B)若E(πB|[u]R)≤E(πP|[u]R), 且E(πB|[u]R)≤E(πN|[u]R), 則u∈BND(C); (N)若E(πN|[u]R)≤E(πP|[u]R), 且E(πN|[u]R)≤E(πB|[u]R), 則u∈NEG(C). 本節將建立面向不完備單值中智信息的三支決策模型.具體的, 將一個不完備單值中智信息系統補全為完備單值中智信息系統, 然后基于補全的完備單值中智信息系統建立三支決策模型. 對于一個不完備單值中智信息系統, 采用平均值法補全未知(缺失)值, 即單值中智數中的未知值用該屬性下其他對象的已知屬性值的平均值代替, 從而一個不完備單值中智信息系統可被補全為一個完備的單值中智信息系統, 稱之為由平均值法誘導的完備單值中智信息系統. 例1表2所示是一個不完備單值中智信息系統(U,A,V,f*), 其中“*”表示該值未知.利用平均值法, 表2被補全為一個完備的單值中智信息系統(見表3). 表2 不完備單值中智信息系統 表3 由平均值法誘導的完備單值中智信息系統 文獻[8]提出了兩個單值中智數之間的相似度如下: 定義6[8]設p=(Tp,Ip,Fp)和q=(Tq,Iq,Fq)是兩個單值中智數, 定義p和q之間的相似度為 基于定義6, 從不完備單值中智信息系統出發, 基于誘導的完備單值中智信息系統給出對象間的相似度的定義. 定義7設(U,A,V,f*)是一個不完備單值中智信息系統,(U,A,V,fc)是由平均值法誘導的完備單值中智信息系統.?u,v∈U, 對象u和v的相似度定義為: (1) 其中#A表示A中屬性的個數,Sai(u,v)=S(fc(u,ai),fc(v,ai))是對象u和v關于屬性ai的相似度. 例2(續例1)根據表3和定義7, 可得對象之間的相似度如下: Sim(u1,u1)=Sim(u2,u2)=Sim(u3,u3)=Sim(u4,u4)=1, Sim(u1,u2)=Sim(u2,u1)=0.4,Sim(u1,u3)=Sim(u3,u1)=0.425, Sim(u1,u4)=Sim(u4,u1)=0.358 3,Sim(u2,u3)=Sim(u3,u2)=0.425, Sim(u2,u4)=Sim(u4,u2)=0.375,Sim(u3,u4)=Sim(u4,u3)=0.35. 進一步給出不完備單值中智信息系統中α相似關系和α相似類的定義. 定義8設(U,A,V,f*)是一個不完備單值中智信息系統,(U,A,V,fc)是由平均值法誘導的完備單值中智信息系統.?α∈[0, 1],U上的α相似關系定義為: SRα={(u,v)∈U×U|Sim(u,v)≥α} ?u∈U,u關于α相似關系SRα的α相似類定義為: 例3(續例2)令α=0.4, 根據定義8, 可得α相似關系SRα如下: SR0.4={(u1,u1),(u1,u2),(u1,u3),(u2,u1),(u2,u2),(u2,u3),(u3,u1),(u3,u2),(u3,u3),(u4,u4)} 進一步, 可得α相似類為: 在三支決策理論框架下, 結合定義3和決策準則(P)-(N)可得面向不完備單值中智信息的決策規則如下: 則u∈POS(C). 則u∈BND(C). 則u∈NEG(C). 其中 本文提出的三支決策模型的關鍵步驟可總結為下面的算法1. 算法1 基于不完備單值中智信息系統的三支決策的算法輸入: 不完備單值中智信息系統、 損失函數和參數α(0<α<1)輸出: 每個對象u∈U的三支決策結果1)將不完備單值中智信息系統中的未知值用該屬性下其他對象對應的屬性值的平均值補全, 得到補全的完備單值中智信息系統. 2)對每個屬性a∈A, 計算對象間的相似度Sa(u, v). 3)由公式(1), 計算對象間關于屬性集A的相似度Sim(u, v).4)計算[u]αSR和P(C|[u]αSR).5)計算期望損失E(π·|[u]αSR)(·=P, B, N).6)基于期望損失計算得分函數sc(E(π·|[u]αSR))和精確度函數ac(E(π·|[u]αSR)). 7)由(P?)-(N?)得到每個對象的三支決策結果. 本節利用一個選擇產品服務商的決策問題的例子, 闡述面向不完備單值中智信息的三支決策模型的有效性和可行性. 隨著互聯網的發展, 數據變得尤為重要, 越來越多的企業開始關注數字化轉型, 利用大數據技術為其服務.為提高數據管理能力, 某公司想要選擇一個數據產品服務商.設U={u1,u2, …,u10}為10個供應商,A={a1,a2,a3,a4}為4個條件屬性(其中a1表示“產品質量”,a2表示“處理能力”,a3表示“售后服務”,a4表示“購買成本”),D=g0gggggg為決策屬性.該領域的專家根據條件屬性為每個供應商給出評價值, 評價值為單值中智數.由于某些原因, 其中一些數據值是缺失的.關于供應商的不完備單值中智信息系統如表4所示, 其中決策屬性值d=1表示專家推薦該供應商,d=0表示專家不推薦該供應商.下面利用本文提出的模型對10個供應商做出評判.給定α=0.37. 表4 關于供應商的不完備單值中智信息系統 由表4可以得到兩個狀態集:C={u3,u4,u6,u9},C={u1,u2,u5,u7,u8,u10}.它們分別代表推薦的供應商集合和不推薦的供應商集合.損失函數如表5所示, 每個損失是一個單值中智數. 表5 損失函數 按照算法1 給出步驟如下: 1)將不完備單值中智信息系統補全為完備單值中智信息系統, 如表6所示. 表6 關于供應商的由平均值法誘導的完備單值中智信息系統 2)根據表6計算對象關于屬性ai(i=1,2,3,4)的相似度Sai(u,v), 這里僅展示Sa1(u,v)(表7). 表7 關于屬性a1的相似度Sa1(u, v) 3)計算對象間的相似度Sim(u,v)(表8). 表8 對象間的相似度 4)由定義8可得對象的相似類: 5)計算期望損失(表9). 表9 期望損失 6)計算期望損失的得分函數和精確度函數(表10). 表10 當α=0.37時期望損失的得分函數和精確度函數 表12 當α=0.365時期望損失的得分函數和精確度函數 表13 當α=0.375時期望損失的得分函數和精確度函數 表14 當α=0.38時期望損失的得分函數和精確度函數 7)根據準則(P*)-(N*), 可得三支決策結果: a)u3,u6,u9∈POS(C); b)u8,u10∈BND(C); c)u1,u2,u4,u5,u7∈NEG(C). 根據上述決策結果, 建議該公司選擇供應商u3,u6或u9; 同時, 供應商u8和u10需要進一步考慮; 而供應商u1,u2,u4,u5和u7則不太合適. 本節討論參數α變化對模型的影響分析.選取α=0.36,0.365,0.37,0.375,0.38, 損失函數的得分函數和精確度函數的結果分別展示在表10-14中.α不同取值產生的決策結果如圖1所示. 圖1 當α變化時的決策結果 由圖1可看出, 隨著α的增大, 被劃分到正域的對象增多.對于決策者來說, 選擇不同的α, 意味著產生不同的決策結果.在處理實際問題時, 需要根據實際情況具體分析, 以選取最適合的α. 本文研究了不完備單值中智信息下的三支決策模型.將不完備單值中智信息系統補全為完備的單值中智信息系統, 基于補全的完備單值中智信息系統計算對象間的相似度, 進一步建立三支決策模型.最后, 利用選擇產品供應商的例子闡述了模型的應用, 并對模型中的參數進行了敏感性分析.本文沒有考慮信息表動態變化的情形, 不完備動態單值中智信息下的三支決策模型是一個有意義的研究課題.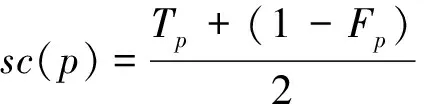
1.2 三支決策

2 不完備單值中智信息下的三支決策模型








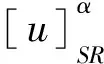





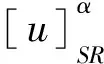





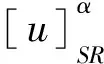



3 模型的應用








4 參數變化對決策結果的影響分析
5 結語

