基于LMS 濾波的復合跟瞄技術研究

閆智輝，劉偉超，趙遠征

(中國船舶集團有限公司第七一三研究所，河南 鄭州 450015)

0 引 言

某艦用綜合體武器系統兼具炮、光發射功能，2 種武器通道共架安裝且共隨動，為保證光通道發射精度，其跟瞄系統采用了粗精復合軸結構。其中粗跟蹤對目標進行捕獲和跟蹤，并將目標引入精跟瞄視場，精跟瞄對視場內的粗跟蹤殘差做進一步校正，實現光束的精確指向。粗、精2 級跟蹤通過光閉環和視場耦合實現級聯、復合跟蹤。

在精跟瞄中，通過驅動快速反射鏡 (fast steering mirror，FSM)偏轉控制光束指向，盡管FSM 具有高帶寬、高精度特性，脫靶量的延遲特性仍然對光束的指向精度有很大影響。如通過提高目標圖像處理幀頻，減小CCD 積分時間，則易引入高頻干擾，并顯著增加圖像處理硬件和軟件上的代價和難度。

魏文軍等[1]在自抗擾控制（ADRC）中采用了預報算法來補償子軸脫靶量滯后的方法。周睿等[2]采用了2 級FSM 分別對窄帶和寬帶擾動進行抑制。文獻[3]采用了自適應PID 的FSM 控制方法。唐清等[4]在既有延遲特性的基礎上，提高了FSM 控制模型的型次。丁科等[5]采用了基于精跟蹤誤差的自適應前饋復合控制。楊東等[6]采用了基于FSM 參考模型的補償方法。上述方法均取得一定控制成效，但著重于提高FSM 動態響應特性和精度方面的研究，未能有效克服精跟瞄脫靶量延遲對指向精度的影響。

粗、精跟蹤具有相互獨立的光電探測通道且共架安裝，兩者脫靶量之間有著固定的空間對應關系。本文提出利用粗跟蹤脫靶量作為精跟瞄參考控制量的方法，針對粗跟蹤脫靶量的高頻非線性和跳變，采用LMS 自適應濾波的方法進行統計學習和濾波補償，并建立基于典型被控對象的某綜合體系統模型進行仿真驗證。

1 復合跟蹤軸和典型被控對象

1.1 復合跟蹤軸結構

復合跟蹤軸結構由粗跟蹤系統、精跟瞄系統組成，如圖1 所示。其中粗跟蹤系統主要包括粗級光電探測和圖像識別單元、隨動系統等，精跟瞄系統主要包括精級光電探測和圖像識別單元、FSM 微位移伺服系統等。

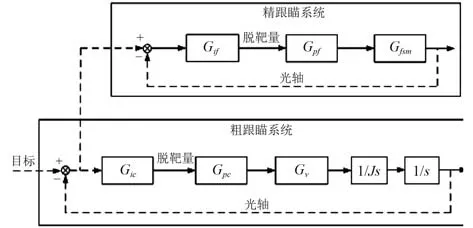
圖1 復合跟蹤軸控制結構Fig. 1 Control structure of combined tracking axis

圖中，Gi和Gif分別為粗跟蹤、精跟瞄的光電探測和圖像識別環節；Gpc和Gpf分別為粗跟蹤、精跟瞄位置控制器；Gv為粗跟蹤隨動系統速度環傳遞函數；Gfsm為精跟瞄FSM 傳遞函數。

粗跟蹤在目指下進行調轉，捕獲目標，給出相對于其視軸的脫靶量，以光閉環的形式控制架體對目標進行穩定跟蹤；目標圖像進入精跟瞄視場后，精級CCD 相機和圖像識別單元對目標進行識別，得到相對于光軸的脫靶量，精位置控制器對脫靶量進行解算，控制FSM 進行偏轉，使目標趨于光軸允許偏差范圍之內。

粗跟蹤和精跟瞄的控制結構相互獨立，通過空間光學耦合實現復合跟蹤，視場取決于各自的探測精度、跟蹤精度、視場匹配性、探測分辨率、光學裝調等要素。目標進入粗、精視場后，粗、精光軸間基線的影響可通過射表進行主動修正或作為固有誤差由FSM 進行被動校正。

1.2 典型被控對象模型

粗精復合跟蹤系統的典型被控對象為隨動系統以及FSM 微位移伺服系統。為提高精度，隨動系統采用力矩電機直驅形式；為提高抗射擊振動和沖擊性，FSM 伺服系統采用音圈電機作動器驅動鏡片偏轉。

直驅隨動系統采用典型的位置/速度/電流3 環控制，其中速度環特性決定動態響應特性，其模型基本結構如圖2 所示。

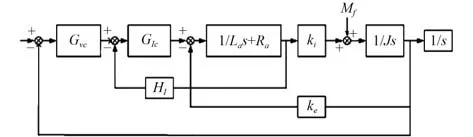
圖2 隨動系統速度環模型Fig. 2 Velocity loop model of servo system

圖中，Gvc和GIc分別為速度環、電流環控制器；La和R分別為力矩電機電感、電阻；ki和ke分別為力矩系數、反電動勢系數；J為負載轉動慣量；HI為電流反饋系數。

經建模和辨識，該直驅隨動系統速度環及慣性負載的等效傳遞函數如下式，3 dB 帶寬約為17 Hz。

式中：Kp=1.005 8；TW=0.009 437 4；Zeta=0.303 03；Tp=0.158 41；Td=0.037 528；Tz=0.074 75。

基于音圈電機驅動的FSM 伺服系統單軸控制模型如圖3 所示。

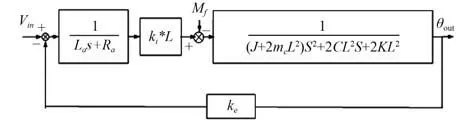
圖3 FSM 單軸控制模型Fig. 3 Uniaxial control model of FSM

圖中，La和R分別為音圈電機電感、電阻；ki和ke分別為力矩系數、反電動勢系數；J為鏡片負載轉動慣量；K為剛度系數；C為等效阻尼系數；L為作動器作用點到偏轉中心的距離；mc為音圈電機動子質量。

經建模和辨識，該FSM 伺服系統的單軸控制模型等效傳遞函數如下式，3 dB 帶寬約為430 Hz。

2 延遲對精跟瞄精度的影響

精跟瞄延遲分量主要包括CCD 積分時間和脫靶量傳輸滯后。以式（2）所示FSM 傳遞函數為被控對象，分別在無延遲、2 ms 延遲（CCD 積分時間1 ms，傳輸延遲1 ms）、3 ms 延遲（CCD 積分時間2 ms，傳輸延遲1 ms）下輸入1 000 μrad，1 Hz 和130 μrad，5 Hz 的正弦信號，精跟瞄精度分別如圖4 和圖5 所示。

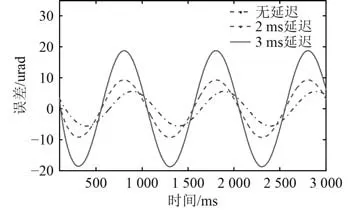
圖4 1 000 μrad，1 Hz 信號控制精度Fig. 4 Control accuracy under 1 000 μrad/1 Hz signal

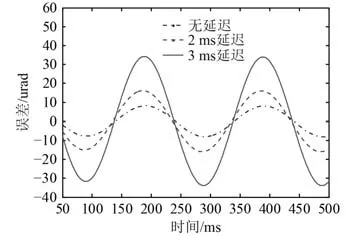
圖5 130 μrad、5 Hz 信號控制精度Fig. 5 Control accuracy under 130 μrad/5 Hz signal

由圖可知，圖像處理幀頻為500 fps（CCD 積分時間2 ms）時，延遲依然對精跟瞄精度有較大影響。圖像處理幀頻提高到1 000 fps（CCD 積分時間1 ms）時，精跟瞄精度有明顯改善，但綜合考慮精跟瞄視場、像元精度等因素，光電探測和圖像識別單元需具備高幀頻、高分辨率的圖像采集、識別性能，這會急劇增加圖像處理器硬件電路、識別算法的設計難度和成本，同時信號傳輸線路也面臨衰減加劇、傳輸距離短的限制。

復合跟蹤軸系統中，粗、精2 級跟蹤雖然具有相互獨立的控制結構，但本質上仍是對同一目標進行識別的不同表現結果。粗跟蹤脫靶量名義上可作為精跟瞄的控制量，由于粗、精采樣頻率和帶寬區別較大，需對粗跟蹤脫靶量進行濾波處理。

3 基于脫靶量的LMS 濾波

3.1 濾波算法的選擇

對于粗跟蹤，盡管目標軌跡會具有一定機動性，但在一定時間周期內目標軌跡仍可按線性建模，利用最小二乘、卡爾曼等濾波算法可以有效補償粗跟蹤脫靶量的滯后。

式（3）是基于CV 模型的最小二乘濾波算法式[7]。

式中：

分別為n，n-1 時刻目標坐標和速度的估計值；zn為測量值，Δt為采樣周期。

式（4）是卡爾曼濾波的主算法式。

對于精跟瞄，則需對粗跟蹤脫靶量進行濾波預測，圖6 和圖7 為典型粗跟蹤脫靶量及其頻譜。式（3）和式（4）中最小二乘濾波和卡爾曼濾波主要包含狀態預計、和估計更新2 部分，而粗跟蹤脫靶量具有明顯的高頻非線性和跳變特性，其狀態預計方程和更新方程難以準確建立，工程實現上，最小二乘、卡爾曼等算法難以獲得理想濾波效果。

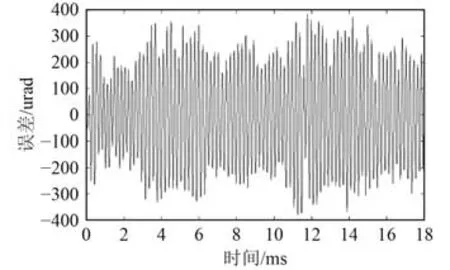
圖6 典型粗跟蹤脫靶量Fig. 6 Typical coarse miss error

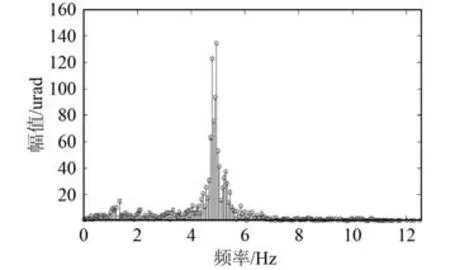
圖7 典型粗跟蹤脫靶量頻譜Fig. 7 Frequency spectrum of typical coarse miss error

鑒于此，本文采用LMS（least mean square）自適應濾波的方法對粗跟蹤脫靶量進行學習和濾波，并作為精跟瞄系統的輸入修正。

3.2 最小均方LMS 自適應濾波

LMS 算法是在維納濾波的基礎上，借鑒最速下降法的思想發展而來的，其目的是使濾波器的均方誤差達到最小。LMS 算法具有以下特點：

1）算法簡易，不需要對回歸量的相關矩陣進行求逆；算法復雜度與FIR 濾波器的維數呈線性關系，算法圍繞此進行；

2）與維納濾波器不同，不需要工作環境統計特性的相關知識；

3）具有一定魯棒性。

LMS 算法結構原理[8]如圖8 所示。

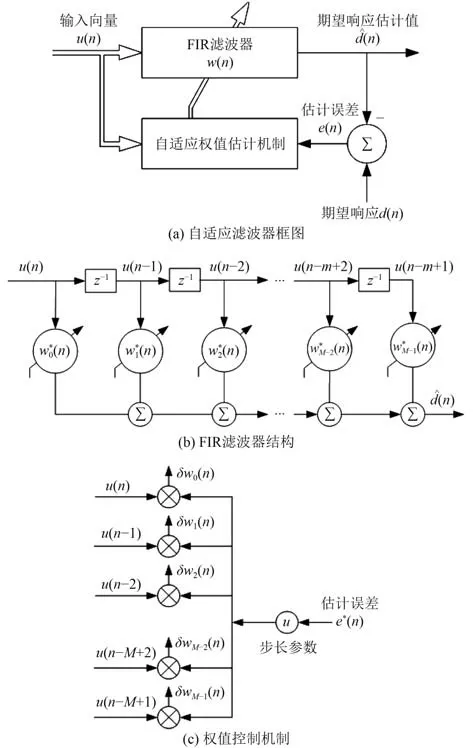
圖8 LMS 算法結構Fig. 8 Algorithm structure of LMS

見圖8，LMS 算法包括3 部分：

1）FIR 濾波器：工作在回歸量（輸入向量）u(n)上，生成期望響應的估計值d(n)；

2）比較器：期望響應d(n)減去估計值d(n)，結果為估計誤差e(n)；

3）自適應權值控制機制，利用估計誤差控制FIR 濾波器上各抽頭w(n)增量的調整。

LMS 算法具體如下：

式中：y(n)為濾波器輸出，u(n)為輸入向量，d(n)為期望響應，w(n)抽頭權向量，μ為步長參數，上標H 表示復共軛轉置，*表示復共軛。

為使局部擾動最小，步長參數需滿足以下條件：

式中，‖u(n)‖2是輸入向量的平方歐式范數。

3.3 基于脫靶量的LMS 濾波結構

LMS 算法采用最速下降法，本質上是一種局部方法，呈現局部最優，其收斂值是較之維納解的次優解，和維納解的差值為額外均方誤差。因此，在濾波補償的基礎上仍需精跟瞄系統自身對額外的均方誤差進行補償。由此，在圖1 的基礎上，建立如圖9 所示的基于粗、精脫靶量的LMS 濾波控制結構。

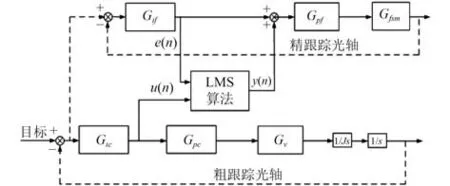
圖9 基于脫靶量的LMS 濾波結構Fig. 9 LMS filtering structure based on miss error

粗跟蹤脫靶量作為LMS 算法中輸入向量u(n)，精跟瞄脫靶量作為估計誤差ef(n)；LMS 自適應濾波器模塊同步采集n個粗跟蹤脫靶量、n個精跟蹤脫靶量的歷史數據，并對每組粗精脫靶量進行代數加權和運算，得出濾波器輸出y(n)，作為精跟瞄參考控制量。

4 仿真及結果

4.1 系統仿真模型

根據圖9，建立如圖10 所示的復合跟瞄系統仿真模型。模型中，0 階保持器將粗跟蹤脫靶量數據周期設定為10 ms，GV&Js為粗跟蹤隨動系統速度環和負載等效傳遞函數；精跟瞄控制周期為2 ms，圖像幀頻為500 fs，延遲時間為3 ms；Gfsm為FSM 單軸等效傳遞函數；目標輸入信號包括粗跟蹤目標模擬信號C t（0.0087 rad，6.28 rad/s）、精跟瞄目標模擬信號Ft（0.13 mrad、31.4 rad/s）、典型粗跟蹤脫靶量At。

圖10 復合跟瞄系統仿真模型Fig. 10 Simulation model of combined tracking system

LSM 濾波器如模型圖11 所示。u取10 組歷史最近粗跟蹤殘差數據，ef取10 組歷史最近精跟瞄誤差數據，step為仿真步長，w(0)～w(9)等10 組抽頭權值按式（7）計算，濾波器輸出y按式（5）計算。

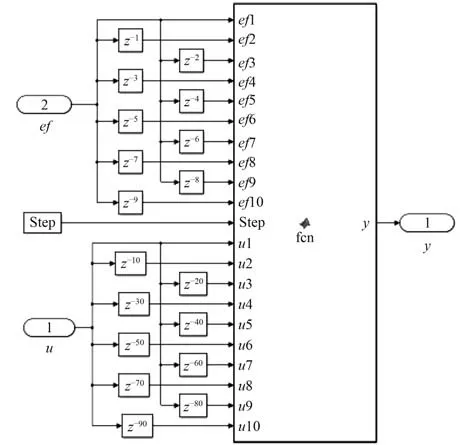
圖11 LMS 濾波器模型Fig. 11 LMS filter model

4.2 仿真結果

1）粗精聯合仿真

向粗跟蹤系統注入Ct（0.0087 rad，6.28 rad/s）目標模擬信號，粗跟蹤殘差曲線如圖12（a）所示，最大誤差約0.8 mrad； LMS 濾波前后，精跟瞄誤差曲線如圖12（b）所示，LMS 濾波前最大誤差約20 μrad，濾波后誤差隨時間減小至10 μrad 內。

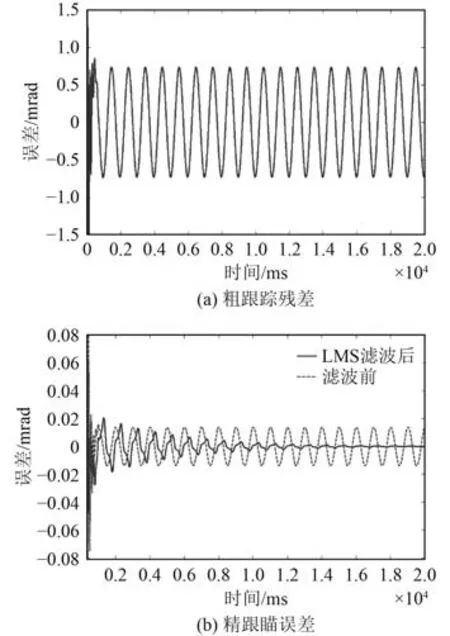
圖12 粗精聯合仿真結果Fig. 12 Co-simulation of coarse and fine system

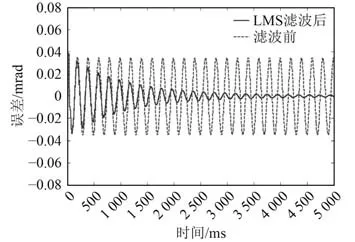
圖13 最大頻率分量信號注入仿真Fig. 13 Injection simulation of maximun frequency signal

圖14 典型粗跟蹤殘差注入Fig. 14 Injection simulation of typical coarse miss error

2）精跟瞄信號注入仿真

向精跟瞄系統直接注入圖6 頻譜中最大頻率分量Ft（0.13 mrad，31.4 rad/s）目標模擬信號， LMS 濾波前大誤差約4 0 μrad，濾波后誤差隨時間減小至最10 μrad 內。

向精跟瞄系統直接注入圖6 中典型粗跟蹤殘差At目標模擬信號， LMS 濾波前均方根誤差約49 μrad，濾波后均方根誤差約12 μrad。

在仿真中，精跟瞄誤差的收斂速度與步長μ成正比，總體來說，μ值不宜過大，以使LMS 算法呈現魯棒性，避免失調。

5 結 語

本文對某綜合體復合跟瞄技術進行研究，針對圖像延遲帶來的指向精度影響，提出并采用對粗、精跟蹤脫靶量進行LMS 自適應濾波和預測的方法，改善了跟瞄精度，且算法結構簡單，魯棒性好，易于實現。具體工程應用時，在收斂且不失調下，可采用變步長方法改善收斂速度。